基于有限元法的车辆桁架式底盘动态分析与优化设计
赵 晶,李家林,钟建华,熊 锐
(1.广东工业大学 机电工程学院,广州 510006;2.福州大学 机械工程与自动化学院,福州 350108)
0 引言
经济发展增加了出行需求,对运输业尤其是客车的运载水平提出了挑战。随着出行需求的增大,行李运载随之增多,导致客车设计需要充分考虑大行李仓结构,而布置大行李仓需要全承载式或带有中部桁架结构的半承载式底盘[1]。车辆底盘车架承载着车辆的主要载荷,并承受车辆行驶过程中的各种力及力矩。底盘式车架的该类特性,决定了其受力的复杂性,使简单的静力学计算与分析难以实现其合理设计与优化[2]。然而,动态分析与优化直接关系到整车性能,对汽车底盘的开发设计意义重大。借助有限元分析方法,可以实现面向需求的底盘车架动态分析与优化[3,4]。
基于有限元方法的分析是实现底盘车架动态分析与优化的有效手段。任可美[4]等运用模态分析方法计算了底盘车架的前十二阶自振动频率,通过参数化优化实现了车架减重及车架激振频率优化。李真[5]等通过对车架模态的多阶模拟,实现了车身的动态性能评价。盛强[6]等通过模态分析获取车架动态特性参数,并实现了参数化设计对车辆动力特性影响的科学性评价。然而,对于中置后驱的客车而言,转向过程中,车身产生扭转,容易导致后轮悬空,但当前大多数研究并未考虑这一工程实际。因此,本研究将重点面向车轮悬空状况,进行底盘车架动态分析与优化设计。
1 桁架式底盘有限元建模与简化
1.1 结构型式确定
该底盘车架主要是由铆焊等方式连接而成的复杂空间结构。主要分三段,前后段采用槽型截面的大梁,中段采用矩形管组焊方法构成桁架结构,其构件主要是由梁、板组成。考虑部件间的干涉,对车架进行建模。
1.2 模型简化与有限元建模
本次优化主要针对中部桁架结构进行分析和优化,且尽可能保证对原结构不做太大改动,同时根据常规分析方法本研究只考虑悬架上部结构,对悬架下部结构不予考虑,并确定了如下三点原则进行模型简化:1)为比较准确地模拟应力集中问题,本次采用板壳单元建模,同时也便于对结构进行细化处理;在划分单元时主要采用四边形单元,局部也采用少量三角形单元;2)在建模过程中略去了一些对分析结果影响很小的工艺孔,以方便网格的划分;3)对于焊接结构,本文采用两种方法模拟:(1)结点重合,即各构件连接处通过单元平滑过渡。这种方法计算结果连续性好,但建模工作量非常大,且连接部件的单元大小有一定差异,这些均给采用结点重合工作带来了许多不便,本项目在尽可能的情况下使用了此种方法;(2)使用MPC单元模拟焊接处,考虑到建模效率,此方法也在局部采用。
通过以上简化方法,本次分析共使用50671个节点,共48873个单元,其中48636个四边形单元,237个三角形单元,另外还有1188个MPC焊接单元,有限元模型如图1所示。

图1 底盘车架有限元模型图
其中,模型所用材料参数及力学性能如表1所示。

表1 模型所用材料力学性能
2 载荷处理与边界条件
2.1 载荷处理方法
本次分析采用集中载荷和均布载荷两种方式加载,即将已知的设备载荷(如表2所示)按集中载荷加载。根据本底盘的承载能力将其他未知的簧载质量(按7吨计算)按均布载荷加载。
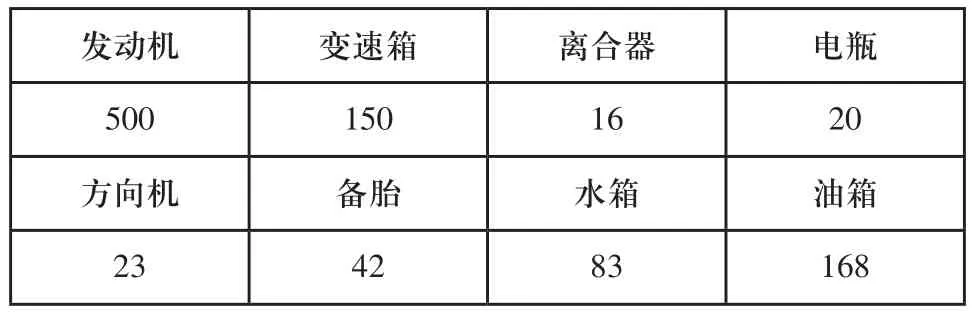
表2 模型加载涉及的各种设备质量(kg)
2.2 加载方式
车架自重通过软件计算直接均布加到各有限元网格节点上;集中载荷按具体安装位置加到有限元网格的相应节点上;均布载荷按质量采用分摊质量法均布加到各有限元网格节点上。
2.3 边界条件
按常规将约束条件放在前后板簧的前后悬置点上,前后板簧悬置点X方向的坐标如表3所示。

表3 板簧悬置点的X方向坐标
2.4 计算工况分类
在计算工况选择上参照相关试验标准(GB/T 6792-1996)和常用计算方法确定边界条件和计算工况。此外,传统计算方法计算扭转工况时均考虑的是前轮悬空,然而对于本研究中的后置发动机的客车来说,后轮悬空更加危险,因此在研究中对于这种工况进行了重点分析。具体工况及对应的载荷形式与边界条件如表4所示。根据原模型的计算结果和对原模型的结构进行分析,拟订如下优化改进方案:
1)原模型YM1:前后段车架与中段桁架组成一体,第四横梁不在前板簧后支座上方,模型骨架质量:662.3kg;
2)原模型YM2:前后段车架与中段桁架组成一体,第四横梁在前板簧后支座上方,模型骨架质量:662.3kg;
3)优化方案YH1:YM2增加中部桁架的上部交叉梁,连在纵梁上,模型骨架质量:682.2kg;
4)优化方案YH2:YM2增加中部桁架的上部交叉梁,连在横梁上,模型骨架质量:684.8kg;
5)优化方案YH3:YH2在后悬处纵梁连接处增加两个斜拉梁,模型骨架质量:688.7kg;
6)优化方案YH4:YH3在桁架间加加强角,模型骨架质量:690.1kg;
7)优化方案YH:YH4+前后段纵梁与桁架立柱加斜撑梁,油箱托架下面增加贯通横梁,模型骨架质量:697.7kg。
3 模态、应力与变形分析评价
3.1 模态分析与评价
车辆运行过程中的激励通过车轮传导到车架,导致车架振动产生。上述激励主要由路面激励、发动机激励、车轮不平衡激励与传动轴激励组成[7]。若车架设计不合理,受到激励时,会因振动引起车架扭曲、弯曲等形变,导致零部件受损甚至动力系统受到破坏[8]。
由于客车所受的激励频率多集中在低频领域,结构的高阶模态对结构的动力学特性影响很小,而前六阶振型为刚体模态,从第七阶开始为弹性模态。本研究重点讨论2.4节中所述的各模型方案下的一阶水平弯曲、一阶垂直弯曲、一阶扭转振型(如图2所示),得到各方案的各阶模态值。

表4 各工况下的载荷形式与边界条件

图2 优化方案(YH)模态分析振型图
结合所提出优化方案的有限元分析振型图和各阶模态值可知,本研究所分析底盘的前几阶固有频率均比较正常,说明计算结果可信有效。在前几阶频率中有与各种激励频率相耦合的地方,在后悬架前端振型不是很平滑,此处由于结构原因刚度变化较大,对此在设计车身时应合理设计,以减小或避免整车和局部共振现象的发生。
3.2 应力分析与评价
对模型进行应力分析,从应力云图(图3、图4)和最大应力对比表(表5)中可以看出:在板簧支座附近应力值较高,与实际情况相符,这一方面是由于计算时在此处设定边界条件,而在边界处理时不可避免地增加了约束刚度,造成了这类区域应力值较高(本研究采用的边界条件为一般参考文献通用的约束方式,相对于其他约束条件,此方法结果较稳定,也较成熟)。另一方面,实际结构在运行时,在此处受力也较集中,在结构设计时也应当引起注意。
在其他一些应力较大的地方大多是在构件结合处,在计算时采用了一部分模拟焊点的单元,增加了局部刚度,造成应力值偏高,同时在这些部位也存在一定的结构应力集中问题,在此处设计上也要注意,尽量减小这部分的应力集中。

图3 优化方案应力分析图-扭转工况(左后轮悬空)

图4 优化方案应力分析图-扭转工况(右后轮悬空)
最终优化方案(YH)与原模型(YM1)各计算工况最大应力值下降数值及百分比如表5所示。根据有关车身承载度的相关成果[9],承载式车身车身承载比例大于0.85;半承载式车身车身承载比例为0.6~0.85;非承载式车身车身承载比例小于0.6。本研究的结构形式应为半承载式,若取车身承载度值为0.7,则底盘的承载度为0.3,按此方法计算则该底盘的实际最大应力值为556×0.3=166.8MPa,低于材料的弹性极限和屈服极限,具有一定的强度储备。
3.3 变形分析与评价
优化后的变形云图如图5、图6所示,结合最大变形量对比表(表5)可知最大变形量及其发生位置。通过分析,可知局部变形协调性很差,变形量较大,如后悬和电瓶托架等处,这些地方在匹配车身时可以得到一定的解决,但在发动机附近车身设计时还应注意与车架的匹配。

图5 优化方案变形分析图-扭转工况(左后轮悬空)

图6 优化方案变形分析图-扭转工况(右后轮悬空)
4 优化改进方案
经过计算,拟定的优化改进的方案如图6所示,其中:改进1)为在中部桁架上部增加交叉梁;改进2)中,此处主要是为了改善刚度突变问题,斜拉梁的结构形式可以根据具体工艺情况决定,也可以将加强板放大,即将加强板与斜拉梁和二为一;改进3)中此处小斜梁下端尽可能延伸到与桁架下纵梁下表面处,并尽可能大以不影响板簧安装和运动为佳;改进4)中,此处小斜梁下端尽可能延伸到与桁架下纵梁下表面处,并尽可能以不影响板簧安装和运动为佳;改进5)中,此处贯通梁以不影响板簧运动和相关管路安装为佳,并尽可能实现与油箱托架一体化设计;改进6)中,以改善此处应力集中并不影响行李仓布置为佳。
5 结束语
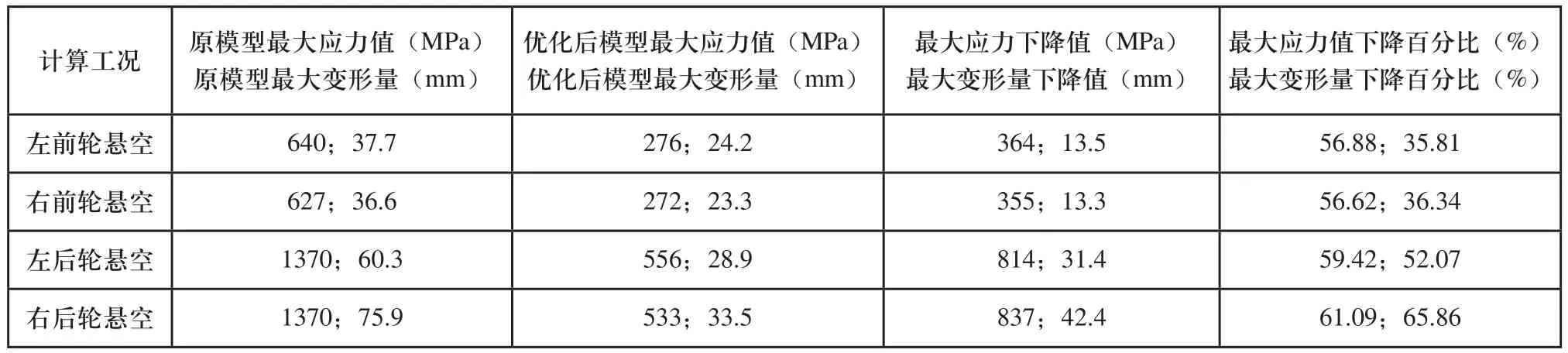
表5 各计算工况最大应力值与最大变形量比较

通过分析可知,原设计方案的车架(YM1,YM2)结构在局部存在较大的应力集中区域,强度、刚度匹配不合理,经过优化后的车架(YH)结构更加合理,在强度、刚度及模态等方面都比原结构要好,虽然车架质量略有增加,仅相当于该车最大总质量的千分之三左右,然而总体最大应力和最大变形量却都下降了50%以上,达到了较好的优化改进效果。

图7 优化改进方案示意图
底盘与车架之间的协调性是影响车身强度的重要因素,不同的底盘与车架搭配对车身强度的影响各异。车身的结构强度,不但取决于车架本身,也受底盘结构及其与底盘组合后的整体构造影响。半承载式车身对于抵抗车架变形、增强刚度、改善车架的应力分布有明显作用。因此建议在匹配车身时能够在中部桁架处和发动机处设计出合理的结构,使其即能满足大行李仓和后置发动机的需要,又能提高整车的承载能力,同时在车架应力集中处应结合车身设计加以进一步改善。

