基于降维Capon的相干信号二维DOA估计算法
刘亚宁,张 秦,郑桂妹
(空军工程大学防空反导学院,陕西 西安 710051)
0 引言
近些年,二维DOA估计成为了研究阵列信号处理的热点,在通信,雷达,探测等领域得到广泛的应用。二维DOA估计一般采用的阵列信号模型包括L型阵列,均匀平面阵列和平行阵列[1-3],但也有一些特殊情况,如文献[4]采用共形阵列,将二维DOA与极化状态进行联合估计。文献[5]在稀疏阵列的基础上,建立基于不动点迭代的空间谱函数,进行二维DOA估计。经典的二维DOA估计算法包括多重信号分类(MUSIC)[6],旋转不变子空间(ESPRIT)[7],传播算子(PM)[8],Capon算法[9]等。但这些经典算法大多存在稳定性差[10],计算量复杂[11]的不足,因此人们在这些传统方法的基础上也提出了不少改进算法。文献[12]提出了一种基于特征空间的MUSIC算法来最大限度的利用信号以及噪声子空间。文献[13]采用Unitary-ESPRIT简化了运算复杂度。闫锋刚等[14]提出了一种半实值Capon算法来降低运算量。
以上所提算法在入射信号相互独立的条件下可以进行有效的估计,但在实际情况下,由于传播环境的复杂性,直射信号和多径传播得到的反射信号会形成相干信号。信号的相干性会导致协方差矩阵不满秩,上文所提算法的估计精度将明显下降甚至失效。为了解决这一问题,学者们提出了不少对应的解相干算法。常见方法有空间平滑算法以及toeplitz矩阵重构法。空间平滑算法应用最为广泛,包括前向空间平滑算法(FSS)和前后向空间平滑算法(FBSS),如文献[12]提出了一种基于特征空间MUSIC的空间平滑算法,文献[15]实现了单快拍下利用空间平滑算法解相干。toeplitz矩阵重构法利用方向矢量的特性,对其线性组合进行toeplitz重排,从而达到解相干的目的,计算精度较高。
本文为了解决相干信号二维DOA估计采用传统方法计算量过大的问题,提出了基于降维Capon的相干信号二维DOA估计算法。
1 降维Capon算法
1.1 信号模型
根据文献可知在常见阵列结构中,L型阵列估计性能最优。因此,本文在L型阵列基础上进行相干信号二维DOA估计。L型阵列在x-y平面上,由分别位于x轴和y轴上的N个阵元构成,阵元间隔为d。设远场空间有k个窄带信号源以不同二维波达方向入射,分别为(θ1,φ1),(θ2,φ2),…,(θk,φk)。其中,θk和φk分别表示第k个信号源的仰角和方位角。且θk∈[-90°,90°],φk∈[-90°,90°],αk和βk分别表示第k个信号源与x轴和y轴夹角。信号阵列模型如图1所示。
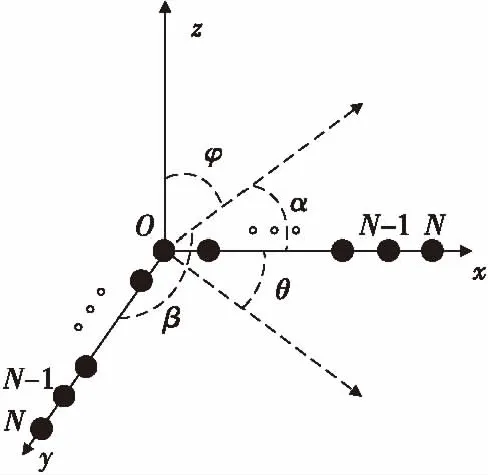
图1 信号阵列模型Fig.1 Signal array model
两个信号的相关系数可表示为:
(1)
当ρij=0时,两信号相互独立;当0<|ρij|<1时,两信号相关;当|ρij|=1时,两信号为相干信号。若信号相干,则x轴和y轴上阵元接收的信号模型为:
X(t)=Ax(θ,φ)S(t)+Nx(t)
(2)
Y(t)=Ay(θ,φ)S(t)+Ny(t)
(3)
式(2)和式(3)中,X(t)和Y(t)分别为x轴和y轴接收信号,Ax(θ,φ)=[ax(θ1,φ1),ax(θ2,φ2),…,ax(θk,φk)]为x轴阵元方向矩阵,ax(θk,φk)=(1,exp(j2πd/λ)cosθksinφk,…,exp(j2π(N-1)d/λ)·cosθksinφk)T,Nx(t)=[n1(t),n2(t),…,nN(t)]为x轴阵元接收到的噪声矢量,Ay(θ,φ)=[ay(θ1,φ1),ay(θ2,φ2),…,ay(θk,φk)]为y轴阵元方向矩阵,ay(θk,φk)=(1,exp(j2πd/λ)sinθksinφk,…,exp(j2π (N-1)d/λ) sinθksinφk)T,Nx(t)=[n1(t),n2(t),…,nN(t)]为y轴阵元接收到的噪声矢量,S(t)=[λ1,λ2,…,λk]s(t)表示相干信号(λk为复常数,s(t)为源信号)。阵元接收噪声为均值为0,方差为σ2的高斯白噪声,并与接收信号独立。
1.2 解相干处理
相干信号的协方差矩阵不是满秩矩阵,故不能直接采用常规二维DOA算法进行估计,本文采用前后向空间平滑算法进行解相干,恢复协方差矩阵的秩,再进行二维DOA估计。首先对x轴阵元进行解相干,将x轴看做由N个阵元组成的均匀线阵,将其划分为Q个子阵,每个子阵有M个阵元,M=N-Q+1。以最左边子阵为参考,则第q个前向子阵的输出为:
AxmDq-1S(t)+Nq(t)
(4)
式(4)中,Axm为子阵对应方向矩阵,D=diag[γ1,γ2,…γk],γk=exp((j2πd/λ)sinαk),Nq(t)为子阵对应噪声矢量。则此子阵的协方差矩阵为:
(5)
则前向空间平滑的协方差矩阵为:
(6)
同理,第q个后向子阵的输出为:
AxmDq-1S(t)+Nq(t)
(7)
式(7)中,Axm为子阵对应方向矩阵,D=diag[γ1,γ2,…,γk],γk=exp((j2πd/λ)sinαk),Nq(t)为子阵对应噪声矢量。则此子阵的协方差矩阵为:
(8)
后向空间平滑的协方差矩阵为:
(9)
(10)
同理,对y轴阵元进行处理后得到的协方差矩阵为:
(11)
因此,L型阵列解相干后的信号协方差矩阵为:
(12)
1.3 降维Capon算法
一般情况下二维Capon算法的空间谱为:
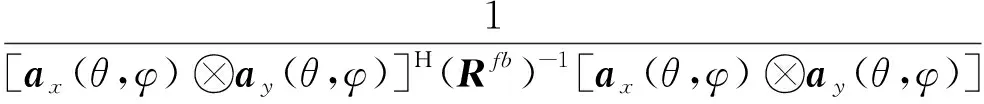
(13)
由图1可推得:
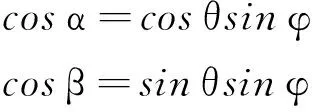
(14)
由式(14)可得:
(15)
因此可得:
ax(θ,φ)=ax(α)=(1,exp(j2πd/λ)cosα,…, exp(j2π (M-1)d/λ)cosβ)T
(16)
ay(θ,φ)=ay(β)=(1,exp(j2πd/λ)cosβ,…, exp(j2π(M-1)d/λ)cosβ)T
(17)
式(13)可表示为:
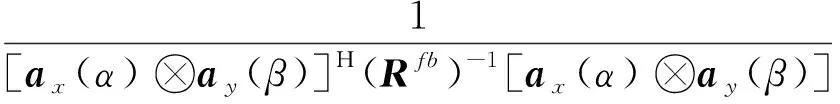
(18)
根据Kronecker积性质可将ax(α)⊗ay(β)转换成[ax(α)⊗IM]ay(β),则式(18)可表示为:
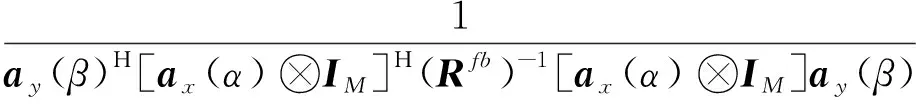
(19)
由于ax(α)∈CM,ay(β)∈CM,Rfb∈CM×M,Capon的运算均为复值运算,一次复值运算包括四次实值运算。如果只进行一次实值运算便可完成DOA估计,则计算量将减少75%,因此本文参考文献方法引入一种半实值Capon算法(SRV-Capon)来完成二维DOA估计。
对协方差矩阵Rfb进行特征值分解可得:
Rfb=SUSSH+NUNNH
(19)
式(19)中,信号子空间S=[u1,u2,…,uk],噪声子空间N=[v1,v2,…,vM-k],uk为Rfb中较大的k个特征值对应的特征向量,vM-k为Rfb中较小的M-k个特征值对应的特征向量。US,UN均为特征值矩阵,其主对角线分别为k个大特征值ξ1,ξ2,…,ξk,和M-k个小特征值。
因为信号子空间和噪声子空间互补正交,因此容易证明:
(Rfb)-1=S(US)-1SH+σ-2NNH=σ-2(SCSNRSH+NNH)
(20)
式(20)中,CSNR=σ2(US)-1。
(21)

(Rfb)-1≈σ-2NNH
(22)
根据二维MUSIC空间谱函数和式(18)、式(22)可得:
f2D-cap(α,β)≈σ-2f2D-music(α,β)
(23)
利用Woodbury公式[12](U+V)-1=U-1-V-1·(I+VU-1)-1VU-1可得:
Re-1(Rfb) =2(Rfb+(Rfb)*)-1= 2(Rfb)-1-2(Rfb)-1(I+(Rfb)*·
(Rfb)-1)-1(Rfb)*(Rfb)-1
(24)
将式(22)代入式(24)得:
Re-1(Rfb) ≈2σ-2NNH-2σ-2HNNH=
2σ-2(I-H)NNH
(25)
式(25)中,H=(Rfb)-1(I+(Rfb)*(Rfb)-1)-1(Rfb)*。
根据矩阵性质可得
Re-1(Rfb)∈R(N)
(26)
将式(24)中Rfb和(Rfb)*互换位置,再按照式(24)和式(25)推导可得:
Re-1(Rfb)∈R(N*)
(27)
结合式(26)和式(27)可得:
Re-1(Rfb)∈R(N)∩R(N*)
(28)
定义式(19)分母为Φ:
Φ=ay(β)H[ax(α)⊗IM]H·
(Rfb)-1[ax(α)⊗IM]ay(β)
(29)
此算法便转化为求Φ最小值时对应的α,β值。设G(α)=[ax(α)⊗IM]H(Rfb)-1[ax(α)⊗IM]。再将(Rfb)-1替换成Re-1(Rfb),因为ax(α)∈CM,ay(β)∈CM,Re-1(Rfb)∈RM×M,所以此运算可看作半实值处理,可得P(α)=[ax(α)⊗IM]HRe-1(Rfb) [ax(α)⊗IM],易得ay(β)Hay(β)=M,则将(29)转化为:
(30)
利用Rayleigh-Ritz理论[16]可得,式(30)的最小值为M×λmin(α),λmin(α)为P(α)的最小特征值,可表示为:
(31)
因此α的估计值可由下式推得:
(32)
由式(28)和式(32)可得:在α的对称角度-α上,也可取到式(30)的最小值,因此,我们可以把搜索范围缩小到原来的一半,但要通过比较G(α)和G(-α)的大小来判断哪一个为正确的α估计值。
其判断标准为:
1)若G(α)≪G(-α),则α为正确估计值;
2)若G(-α)≪G(α),则-α为正确估计值;
3)若G(-α)≈G(α),则α和-α均为正确估计值。
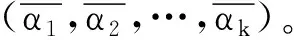
ay(βk)=emin(P(αk))
(33)
定义φk=angle(ay(βk)),结合式(17),可得:
φk=[0,(2πd/λ)cosβk,…,(2π(M-1)d/λ)cosβk]T
(34)
利用式(25)估计βk可采用最小二乘法[17],令:
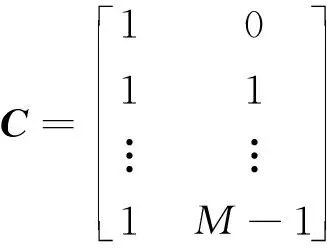
(35)
即求解min‖Cdk-φk‖2,可得其结果为:
(36)
式(36)中,dk(2)为结果值,则βk可由下式得:
βk=arcsin(dk(2)/(2πd/λ))
(37)
2 相干信号二维DOA估计算法
2.1 算法流程
本文所提基于降维Capon的相干信号二维DOA估计算法流程为:
步骤1)先采用FBSS解相干,得到阵元数为M的子阵的满秩协方差矩阵。
步骤2)提取子阵协方差矩阵的实部,代入一种半实值Capon算法进行DOA估计。
步骤3)利用Kronecker积的性质求出P(α)的最小特征值,代入式(32)得到α估计值,再根据G(α)的判断标准筛选出正确的α估计值。
步骤4)根据式(33)—式(37),得到β估计值。
步骤5)按照式(15)得到二维DOA估计值。
2.2 计算量分析
按照上述步骤分析本文算法的计算量,并与常规二维Capon算法(2D-Capon)进行对比,设快拍数为L,搜索点数为n,子阵个数为M。
步骤1)解相干求满秩协方差矩阵的计算量为O{(N-M)L(2M+3)}。
步骤2)求最小特征值以及筛选正确估计值的计算量为O{n[(M2+M)-K(M+1)]+5M2K}。
步骤3)求β估计值的计算量为O{10M}。
步骤4)计算量可以忽略不计。
综上可得总计算量为O{(N-M)L(2M+3)+n[(M2+M)-K(M+1)]+5M2K+10M}。而常规二维Capon的计算量为O{(N-M)L(2M+3)+4n(M2+M)+4M2K+10M}。
为直观表示,给出具体数值作图2来对比两种算法的计算量大小。设N-M=2,快拍L=100,信号个数K为3,搜索点数n=3×103,由图2可得,本文算法相比常规二维Capon算法计算量显著减小,可比常规算法减少接近75%。
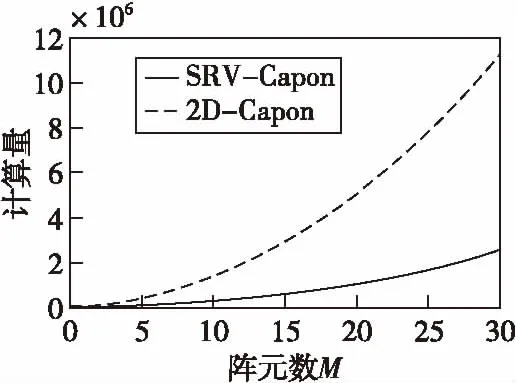
图2 两种算法计算量对比图Fig.2 Comparison chart of two algorithms’ computation complexity
3 仿真验证
3.1 算法的正确性验证
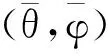
(38)
式(38)中,Eθ为方位角的标准误差,Eφ为仰角的标准误差。
为了验证本算法,进行如下仿真。假设阵列为平面阵列,有3个窄带信号入射到阵列上,其入射角度分别为(15°,10°),(25°,35°),(40°,50°)。x轴,y轴方向阵元个数均为8,子阵个数为6,阵元间隔d=λ/2,角度搜索精度为0.01°。快拍数L为50,信噪比SNR为20 dB,进行500次蒙特卡罗实验。图3目标二维DOA估计值显示了三个信源条件下本算法的估计结果。从图中可看出,对三个目标的入射角度估计基本保持在真实值周围,波动较小,表明本算法能正确对二维DOA进行估计,并且精度较高。
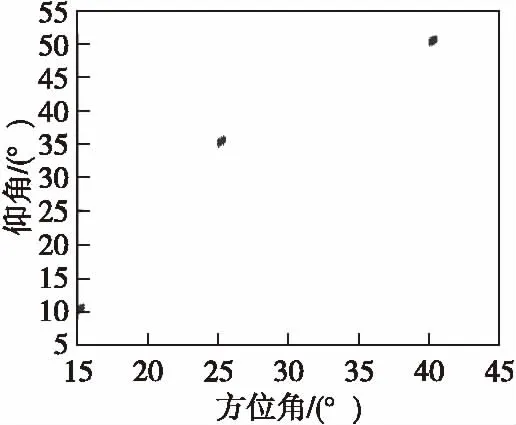
图3 目标二维DOA估计值Fig.3 Estimation of target 2D DOA
3.2 信噪比与估计性能的关系
采用同4.1节相同的实验验参数,蒙特卡罗实验次数为500,快拍数为50,x轴,y轴方向阵元个数均为8,子阵个数为6,信噪比分别取-4 dB,0 dB,4 dB,8 dB,12 dB,16 dB,20 dB。将本文算法与2D-Capon和常规二维MUSIC算法(2D-MUSIC)进行比较,结果如图4所示。
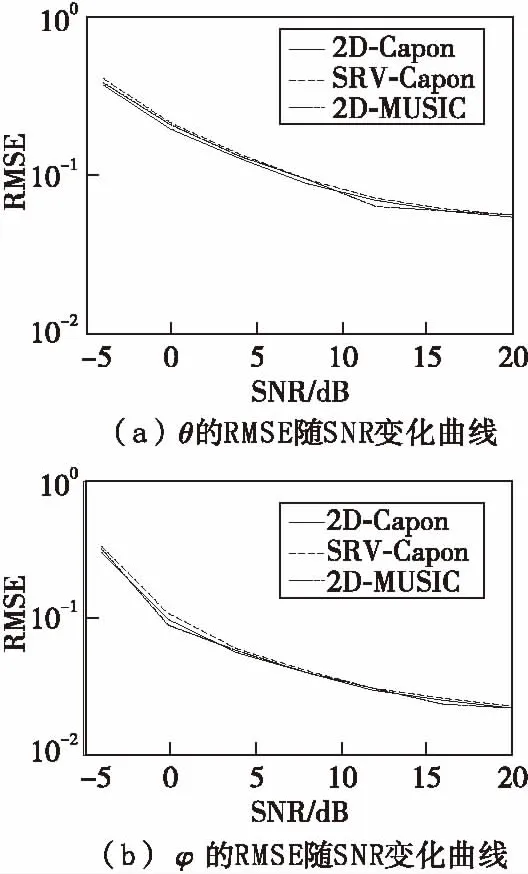
图4 RMSE与SNR关系图Fig.4 The relationship between RMSE and SNR
由图3可得,本文算法和2D-Capon和2D-MUSIC算法在信噪比较小的时候有一定差距,但随着噪比增大,差距差距逐渐缩小,估计精度基本相同,且两个角度的估计值RMSE随信噪比的增大逐渐减小,说明估计性能逐渐变好,但减小的趋势越来越缓。
3.3 快拍数与估计性能的关系
采用同4.1节相同的实验参数,蒙特卡罗实验次数为500,x轴,y轴方向阵元个数均为8,子阵个数为6,信噪比取20 dB,快拍数分别为10,20,40,60,80,100,120,140,160。将本文算法与2D-Capon和2D-MUSIC进行比较,结果如图5所示。
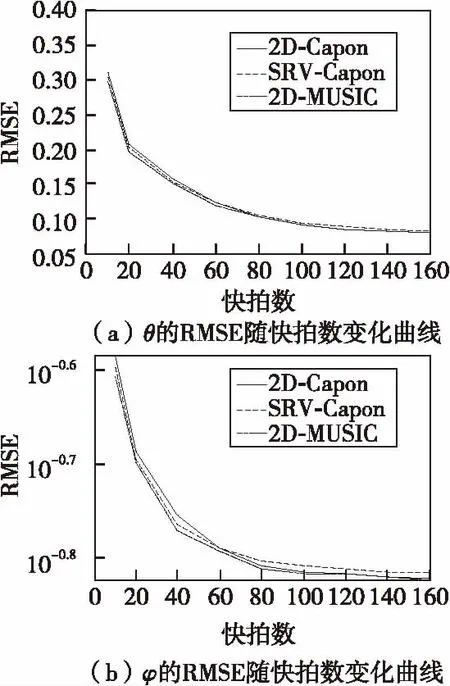
图5 RMSE与快拍数关系图Fig.5 The relationship between RMSE and snapshot
由图5可得,当快拍数小于40的时候,本文算法RMSE小于2D-Capon,本文给出的分析是在小快拍下,信号相关性较大,复数域范围的协方差矩阵相比于实数域范围的协方差矩阵秩亏更大,因此有可能导致2D-Capon估计性能不如SRV-Capon。当快拍数较大时,本文算法相比2D-Capon和2D-MUSIC算法基本相同。随着快拍数的增大,RMSE值减小,但RMSE值减小的趋势越来越缓。说明虽然估计性能越来越好,但变好的趋势是越来越缓。由于快拍数的选择影响算法的计算复杂度,因此并非快拍数越大越好。
4 结论
本文提出了基于降维Capon的相干信号二维DOA估计算法,该算法采用空间平滑和半实值降维Capon算法,相比常规二维Capon算法,计算量显著减小,仿真结果表明本文算法的估计性能与常规二维Capon算法和二维MUSIC算法基本相同。

