改进卡尔曼滤波的对流层散射多径噪声抑制方法
吴文溢,熊益波,王雷元,李艳洁,陈西宏
(1.西北核技术研究所,陕西 西安 710024;2.空军工程大学防空反导学院,陕西 西安 710051)
0 引言
对流层散射多径效应是影响对流层散射双向时间比对(Two Way Troposphere Time Transfer, TWT3)系统[1-3]通信质量的关键因素,研究对流层散射多径时延模型和多径噪声抑制方法对TWT3系统设计和性能提升具有至关重要的作用。目前国际上采用的多径抑制方法主要有窄相关法[4],Bayesian法[5],波形分解法[6]等,这些方法通过建立直达信号的函数统计模型来抑制滞后于直达信号的多径信号,需考虑相关间隔和预相关带宽,且相关器数量繁多。通过最大似然估计、粒子滤波和小波滤波等信号估计方法能有效地抑制多径效应,文献[7]提出一种基于自适应盲均衡和回归最小二乘相结合的削弱GPS动态多径效应的算法,通过仿真表明该算法能够较好地减小多径对载波相位和延迟的影响。文献[8]提出了一种结合无迹卡尔曼滤波和小波阈值自适应滤波的混合粒子滤波算法,削弱了多径影响。
现有的多径抑制模型多是针对镜面多径的情况,而散射多径在接收端表现为大量多径信号的叠加,通常可视为附加一个噪声通道[9]。考虑到对流层散射信道的复杂性和随机性,其直达信号的函数统计模型难以建立,因此,目前尚未有对TWT3系统的散射多径噪声进行抑制的普遍方法。文献[10]针对TWT3系统的多径抑制问题,提出了基于Kalman滤波的散射多径抑制方法,分析了不同基线距离和波束宽度下的最大多径时延扩展量,建立了TWT3系统的多径滤波模型,通过仿真验证了该方法能有效提升钟差数据的精度和稳定性,但该模型假设条件是系统过程噪声和观测误差噪声均为高斯白噪声,并没有考虑测量系统性误差的影响。在对流层散射双向时间同步应用中,由于散射信道多径效应复杂性和随机性带来的系统误差的干扰,将极大可能地影响卡尔曼滤波的精度和准确性,甚至使得滤波结果发散[11]。本文针对此问题,提出了基于增广参数KF的散射多径噪声抑制方法。
1 基于Sunde散射模型的多径时延模型
对流层散射信道是无线电通过对流层中散射体进行传播而形成的一种典型的时变多径衰落信道。在图1中,对流层中存在相当大数目的散射体在收发天线波束交汇形成的公共体积中进行了二次辐射,由于散射体随机错落分布在公共体积的不同空间处,当时间信号通过散射体由发射机向接收站传播时,接收天线将会收到经不同路径到达且存在时延差异的各个信号的合成信号,该合成信号在时域上将表现为相对于原信号的时延扩展。在数字通信中,散射多径信道的这种时散特性对时间信号的传输是十分有害的,不但可能会导致信号波形失真,而且会造成较严重的符号间干扰,这种现象称为频率选择性衰落[12]。为了减少码间干扰对正确码元的比例,避免造成错误判定,通常会增加码元宽度,而这将极大地限制散射通信的传输速率,因此,建立合适的多径时延模型对TWT3系统最大传输速率和最佳波形设计至关重要。
事实上,对流层散射多径时延与散射体的分布是紧密相关的。这些对流层中的散射体可以理解为不均匀的大气扰动,由于受到温度、湿度以及大气压强等因素影响,散射体的形状、尺寸和密度无时无刻不在变化,其介电常数同样也在不断变动。图2为Sunde散射信道模型简易图,Sunde模型给出了以下几条假设[13]:
1)由于不同路径的接收信号之间不相关,因此对流层散射信道为多条独立路径的连续集合;
2)设收发站之间信号最短路径的传播时延为T0,则其余的路径时延表示为T(x)=T0+δ(x),δm(x)表示最远路径与最短路径的最大多径时延差;
3)散射能量按照路径延迟均匀分布。

图2 Sunde散射信道模型Fig.2 Sunde scattering channel model
对流层中的散射体对流层中的散射体对于无线电信号是有方向性的,可近似等效为一个定向的天线,具有散射方向图(见图3),且散射角越大,散射信号强度越弱[14]。这在理论和实践中均可说明。在Sunde模型中,散射体依照散射角的变化而分成不同的层,每一层有着相同的散射角。由于电波传输损耗与散射角有关,假设在每一层中的各个路径信号到达接收端时的能量相同。接收端信号的接收认为是不同层的信号叠加。不同层有着不同的散射角,一般来说,随着散射角的增大,散射信号能量不断降低。
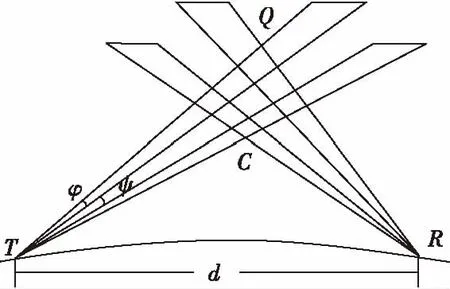
图3 散射场方向图Fig.3 Scattering field pattern
假定收发天线均水平放置,则可知在图3中,径TCR的无线电信号传播路径最短,径的路径最远。径TCR和径TQR的路径延迟可以表示为:
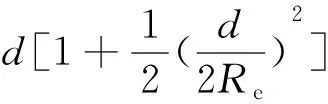
(1)
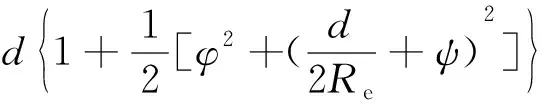
(2)
式(1)、式(2)中,φ和ψ分别表示天线波束的水平和垂直角度(单位:rad),d表示收发两站间的通信距离(单位:km),Re表示等效地球半径,取Re=8 500 km。
最大多径时延δm是可以用来描述多径时延展宽的重要特征参数,可通过径TQR的路径减去径TCR的路径除以光速表示:
(3)
式(3)中,c表示光速,取300 000 km/s;θ0表示最小散射角。
由上述多径时延模型可知,对流层散射信道的最大多径时延δm与通信距离d,收发天线的水平波束宽度φ,垂直波束宽度ψ,散射角大小θ以及地理环境等因素相关。考虑在同一垂直平面的路径延迟情况(φ=0°),将天线水平放置(仰角为0°),实际应用中,受地貌环境的影响,天线仰角会略有增加,但一般不会超过5°。天线的波速宽度与天线的尺寸有关,天线尺寸D=2 m时,其波束宽度ψ一般为2.5°,而D=3 m时,ψ≈1.2°,表1是ψ取不同值时,计算得到不同通信距离d相对应的最大多径时延δm。
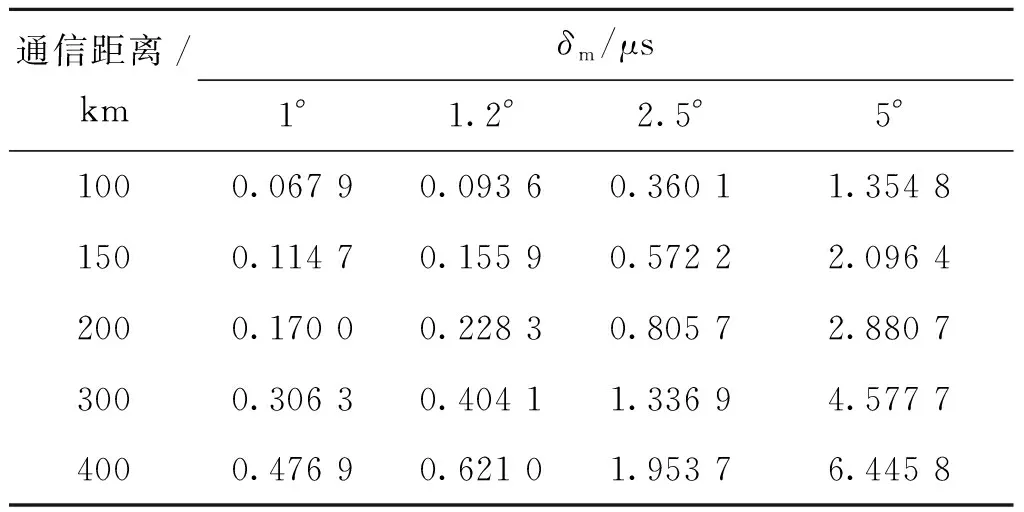
表1 不同通信距离的最大多径时延Tab.1 Maximum multipath delay with different communication distance
如表1所示,最大多径时延δm随着通信距离和波束宽度的增加而增大,通信距离为300 km,波束宽度为1.2°时,对应最大多径时延可达到0.4 μs。在TWT3系统中进行双向时间信号传递时,路径延迟可相互抵消95%~98%,最大多径时延可达到纳秒量级。
2 对流层散射多径噪声抑制
多径效应误差是TWT3系统的重要误差来源,研究散射多径抑制方法对提升TWT3系统时同精度意义重大。对流层散射信道多径效应具有随机性和连续性,接收天线接收到的是各个信号的叠加,通常表现为一个附加的噪声通道。TWT3系统中收发站在传递时间比对信号时,由于对流层散射信道多径效应的影响,在接收站的信号会产生较大的时延扩展,相当于附加了一个多径噪声,观测钟差会存在较大的抖动,极大地抑制了系统的性能。卡尔曼滤波是一种参数最优估计方法,能有效地从带有色噪声干扰的信号中提取有用信号实现信号估计,提升系统时间比对精度。
2.1 卡尔曼滤波
卡尔曼滤波[15-16]是典型的最小方差估计方法,通过不断地修正和更新,获取后验概率的误差协方差最小的估计值实现最优滤波,因此,卡尔曼滤波非常适合实时动态数据处理。
Kalman滤波离散模型由状态方程和观测方程来进行描述:
Xk=Φk,k-1Xk-1+Wk
(4)
Lk=AkXk+ek
(5)
式(4)、式(5)中,Xk为状态向量,Lk为观测向量,Φk,k-1为系统状态转移矩阵,Ak为观测矩阵,Wk为系统过程噪声向量,ek为观测误差噪声向量。系统过程噪声Wk和观测误差噪声ek的统计特性满足下式:
(6)
差噪声式中,δkj为均值为零的高斯白噪声序列,Qk为系统过程噪声Wk的正定方差矩阵,Rk为观测误差噪声,ek的正定方差矩阵。
Kalman滤波有两个更新过程:时间更新和量测更新。时间更新实质是预测,推算当前状态变量和误差协方差估计 ,为下一时刻进行先验估计;量测更新实质是修正,利用观测值和上一时刻的先验估计进行反馈,以得到改善的后验估计。
2.2 基于增广参数Klman滤波的多径噪声抑制方法
Kalman最优估计的假设条件是系统过程噪声向量Wk和观测误差噪声向量ek均为高斯白噪声,忽略了系统误差的影响。在对流层散射双向时间同步应用中,由于散射信道多径效应系统误差的干扰,将极大可能地影响卡尔曼滤波的精度和准确性,甚至使得滤波结果发散。因此,本文考虑将多径系统误差作为状态参数增广状态向量,并利用一阶AR模型对系统误差进行建模,从而补偿滤波来抑制滤波参数估计中系统性误差的影响,提高卡尔曼滤波的精度和可靠性。
由式(6)可知,卡尔曼滤波是假定Wk、Wj、ek、ej之间互不相关且Wk和ek的数学期望为0,但由于对流层散射多径效应的随机性和复杂性,在实际观测中观测误差ek的期望可能出现不为零的情况,即:
(7)
若忽略系统误差uk的影响,得到的卡尔曼估计值是有偏的。当观测误差ek的期望不为零时,ek可以用下式表示:
ek=uk+δk
(8)
式(8)中,δk为均值为零的高斯白噪声序列。
建立观测噪声系统误差uk的函数模型通常需要一些先验信息,如量测对象、实验条件等,根据TWT3系统的对流层散射多径效应特点和有色噪声函数模型,利用一阶AR模型建立观测系统误差模型[17-18],具体表达式如下:
uk=ψk,k-1uk-1+ηk
(9)
式(9)中,ψk,k-1为观测系统噪声状态转移矩阵,ηk为均值为零且协方差为正定矩阵的高斯白噪声序列。
系统误差具有复杂性、延续性和偶然性,在进行观测系统误差状态转移矩阵ψk,k-1的设计时,必须考虑对流层散射多径效应的特点。现对系统误差uk作一些近似的假设,认为uk在极短的时间间内变化微小且具有随机波动性,其模型可以表示为:
uk=uk-1+ηk
(10)
再将建立的观测系统误差模型作为状态参数纳入状态方程中,增广状态向量,并对观测方程也进行扩增。对于TWT3系统,其观测钟差受初始钟差、原子钟频率不稳定性变化率等因素的影响,具体表达式为[19-20]:
(11)
式(11)中,τ(t)表示观测钟差,τ0表示初始钟差,f0为标准额定频率,df为频率变化恒量,ρ为用来描述频率不稳定性的相关频率噪声,对于频率稳定性能良好的原子钟来说,式(11)的末项可忽略不计。
因此,对于TWT3系统对流层散射信道,可建立状态和观测方程为:
(12)
式(12)中,dtk中表示测量间隔。
根据式(8)—式(10)建立的系统误差的模型,下面推导增广参数卡尔曼滤波的状态方程和观测方程:
(13)
简化可得:
(14)
3 算例与结果分析
为了能验证上述方法的效果,设计了对流层散射时钟信号传输试验。图4为对流层散射传递时间信号的框图。试验中采用的铷钟型号为PRS10型铷原子钟,时间间隔测试仪的型号为Agilent53132A。
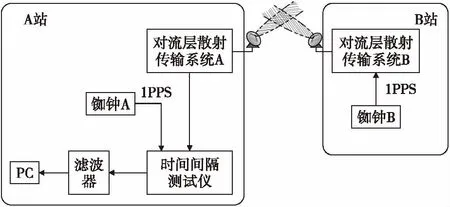
图4 对流层散射传递时间信号框图Fig.4 Diagram of tropospheric scatter transmission time signal
图5为试验获取的钟差数据,采样时长为2 h,间隔为2 s,测量结果如图所示。
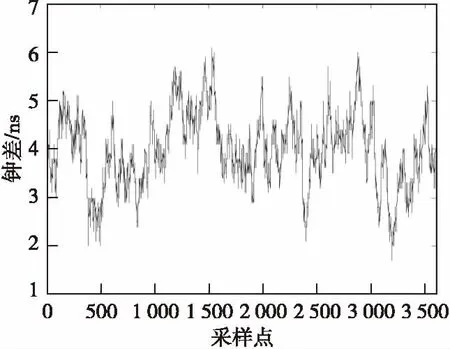
图5 观测钟差数据序列Fig.5 Sequence of clock error data
时间间隔计数器(Time Interval Counter,TIC)测得的钟差主要受设备时钟、多径效应以及系统自身热噪声等因素的影响。由于对流层散射多径效应具有随机性和重复性的特性,图6的钟差序列不仅含有高频的观测随机噪声误差,且含有低频的系统性误差,其中具有重复性的部分主要表现为低频的系统性误差。为了更好地利用观测数据,取钟差序列中的第0~300,300~600,600~900,900~1 200,1 200~1 500,1 500~1 800,1 800~2 100,2 100~2 400,2 400~2 700采样点记为样本A~I,然后再对相邻样本求取最大相关系数,结果见表2。
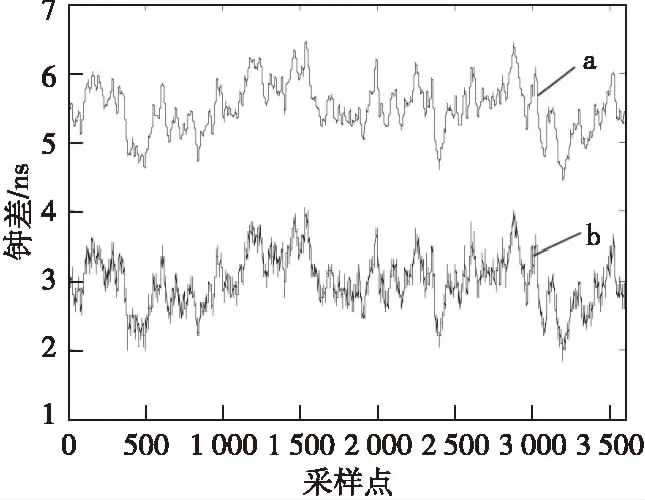
图6 钟差序列Fig.6 Clock difference sequence

样本A-BB-CC-DD-EE-FF-GG-HH-I相关0.960.970.970.980.990.970.980.97
从表2中可以看出,样本间的钟差数据具有较强的相关性,这也进一步说明散射多径效应的重复性使得观测钟差序列中包含低频系统误差。为了能比较本文所提出的卡尔曼滤波算法的效果,采用db8小波对钟差序列进行强制消噪处理,将滤波后的钟差序列作为多径模型,用于之后卡尔曼滤波算法改正。多径误差改正模型的钟差序列中已去除了高频随机噪声,只包含低频系统噪声。图6中b表示观测钟差序列,a表示经db8小波消噪后的多径误差改正模型。为了使a和b能在同一图中显示,将a的钟差序列沿纵轴向上平移了5个单位。
采用两种方案对观测钟差序列进行处理。方案一:采用卡尔曼滤波算法对观测钟差序列样本A~I进行滤波;方案二采用本文提出的增广参数卡尔曼滤波改进算法对观测钟差序列样本A~I进行多路径系统误差改正,同时更新多径误差改正模型。限于篇幅,这里只给出了样本A~D中连续的50个采样点的结果,图7表示两种方案的滤波结果,图8表示方案二中增广参数卡尔曼滤波估计的系统误差序列图。
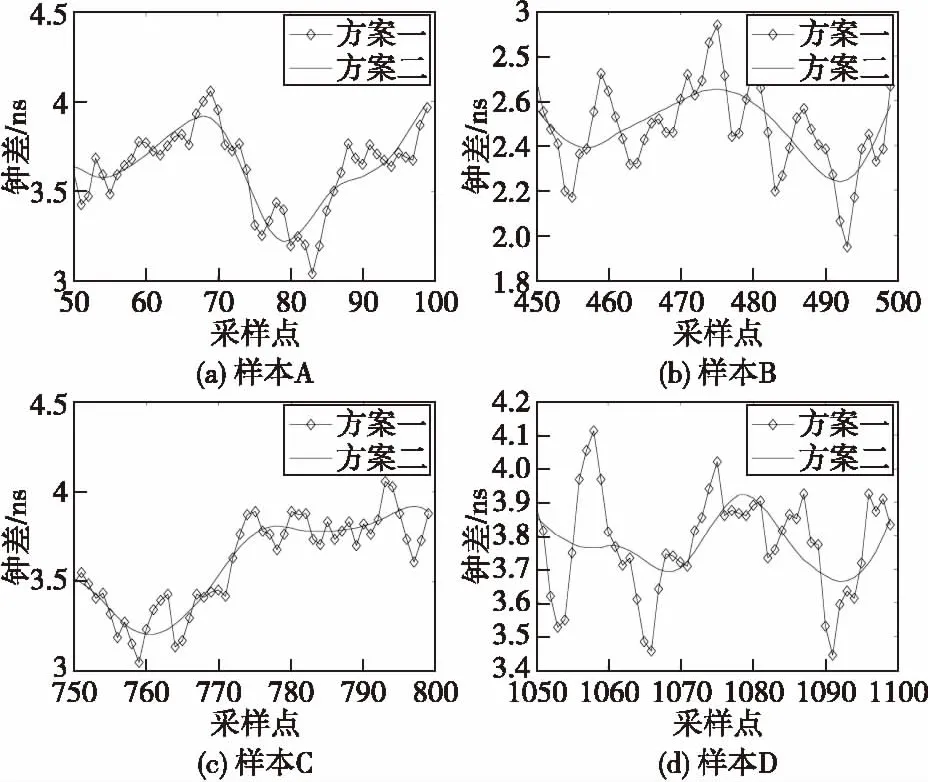
图7 两种方案滤波结果图Fig.7 Filtering results of two schemes
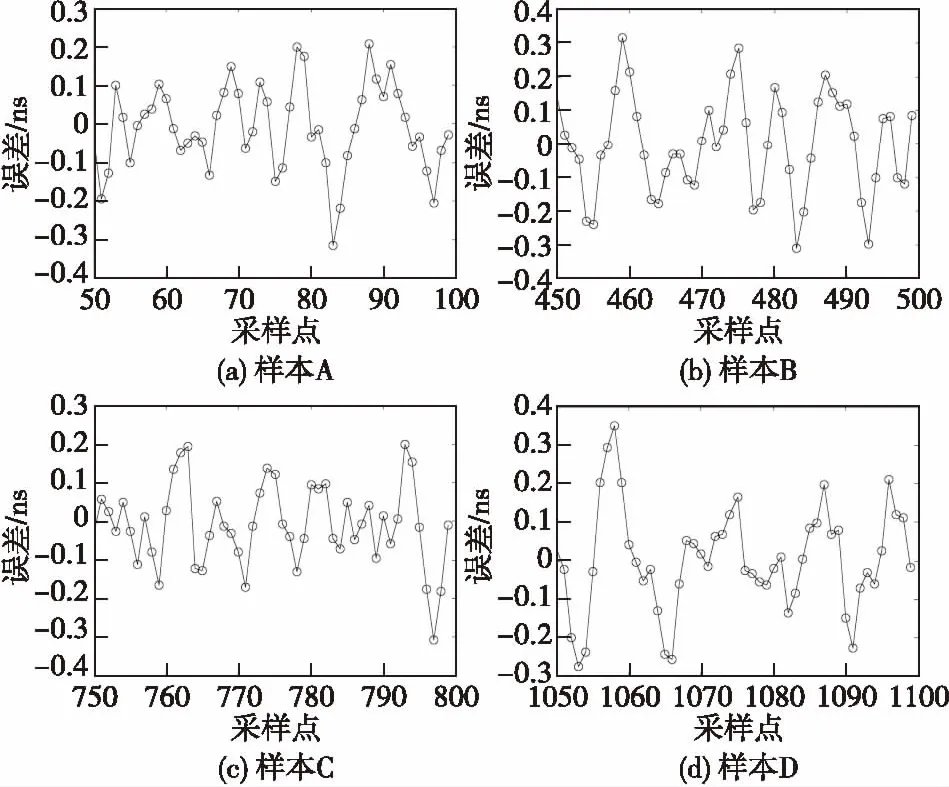
图8 方案二中系统误差估计序列图Fig.8 Sequence diagram of system error estimate in scheme 2
为进一步验证本文所提出的增广参数卡尔曼滤波算法的精度,采用均方根误差(Root Mean Square Error, RMSE)来比较滤波前后的准确性,采用阿伦方差(Allan Error, AE)进行比较两种模型滤波前后钟差的稳定性,即:
(15)
(16)
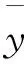
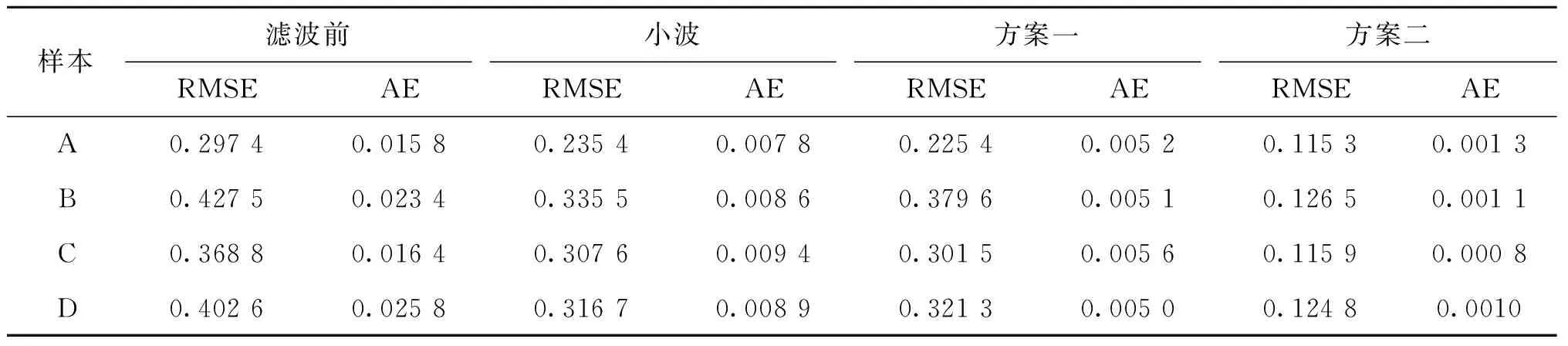
表3 不同模型误差统计结果Tab.3 Statistical results of different model errors ns
分析图6—图8和表3中的计算结果,可以得出以下结论:
1)小波滤波和Kalman滤波均能抑制多径噪声,且Kalman滤波结果要略好于小波滤波结果。从表3中的RMSE统计结果来看,经过小波或Kalman滤波后的钟差仍含有较大的噪声,这主要是低频系统噪声的影响,同时也说明小波滤波和Kalman滤波能滤除随机噪声,但对系统性误差的抑制效果较差。
2)从表3中AE的统计结果来看,频率稳定性由滤波前的E-11量级,提升到方案二的E-13量级,符合试验中使用的铷原子钟频率稳定度的量级标准。这表明本文提出的基于增广参数Kalman滤波方法能有效地抑制多径效应带来的噪声抖动,提高系统精度和稳定性。
3)结合图7、图8和表3中的计算结果来看,经过方案二算法滤波后的钟差较滤波前的精度提升了50%以上,这表明基于增广参数Kalman算法能有效地抑制系统中由对流层散射多径效应带来的多径噪声误差。此外,基于Kalman滤波的多径抑制算法实时性较好,能满足TWT3系统实时快速时间同步的需求。
4 结论
本文提出了抑制对流层散射多径噪声的算法,该算法利用一阶AR函数模型对系统误差建模,并将其增广状态向量,有效地抑制了多径系统中系统噪声的干扰,通过设计对流层散射时钟信号传输试验对算法进行检验,仿真和计算结果表明了该算法的准确性和可靠性。该方法能有效抑制系统噪声的干扰,同时在提升TWT3系统同步精度的工程实现方面具有重要意义。

