基于集合经验模态的小波半软阈值降噪

甄龙信，王云龙，邓小艳，张伟锟

(燕山大学车辆与能源学院，河北 秦皇岛 066000)

0 引言

实际工程采集的振动信号，由于环境和采集设备等因素的影响，采集的信号中会混有一定噪声，为降低信号分析误差，在分析前要做降噪处理，目前常用的降噪方法包含小波[1-4]、经验模态分解(Empirical Mode Decomposition, EMD)[5-7]等,降噪效果将直接影响信号的分析结果。Donoho等[8-9]在1995年提出硬阈值和软阈值的信号降噪法并推导出了通用阈值公式，但硬阈值函数降噪后信号连续性与光滑性均变差、软阈值函数降噪后信号在重构过程出现一定偏差。Gao等[10]在Donoho提出的硬、软阈值基础上提出半软阈值函数，证明小波半软阈值函数在一定程度上弥补了两者的缺陷。Huang等[11]在1998年提出EMD降噪法，由于EMD在降噪过程中产生模态混叠的现象，在此基础上Huang提出了改进-集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)降噪法。小波阈值降噪法对非平稳信号降噪效果不太理想，EMD降噪法通过直接去除信号的高频部分达到降噪目的，相应高频分量上的部分有用信息将被剔除，导致信号失真。据此，杜修力等[12]首次提出EMD与小波软或硬阈值联合降噪的方法，验证了该方法的有效性和稳定性。苏秀红等[13]利用EMD和小波阈值对冲击信号降噪，其效果优于单纯的EMD降噪法和小波阈值降噪法。饶运章等[14]结合EMD和小波阈值法对爆破震动信号降噪，该方法能够有效去除爆破震动信号中的噪声。在EMD和小波阈值联合降噪过程中，因EMD分解造成的模态混叠现象影响降噪效果，本文针对此问题，提出了基于集合经验模态的小波半软阈值降噪方法。

1 集合经验模态分解方法

EEMD作为EMD的改进在一定程度上避免了IMF分量模态混叠的现象。EEMD是在EMD分解过程中加入随机高斯白噪声，利用高斯白噪声的零均值特点使得噪声在添加过程中相互抵消，最后得到IMF分量。其具体步骤如下[15]：

1)多次在源信号x(t)中加入随机高斯白噪声；

xi(t)=x(t)+ui(t)i=1,2,…,N

(1)

2)对各xi(t)进行EMD分解得到各组加入白噪声的IMF分量IMFij和分解余量ci(t)

(2)

式(2)中，j=1,2，…,M，表示为各xi(t)分解层数；

3)将各次求得的IMF分量和余量ci(t)做均值化处理得到分量IMFj和余量c(t),即

(3)

(4)

2 基于EEMD的小波半软阈值降噪

2.1 小波阈值函数

小波阈值降噪法通过选择合适的阈值对信号中的噪声进行抑制，故阈值函数的选取是影响小波阈值降噪效果的主要因素。

1)硬阈值函数

(5)

式(5)中，X为小波分解系数，Y为阈值量化后的小波系数，λ为给定的阈值。

小波系数经硬阈值函数处理后连续性变差，重构过程中信号会出现波动，降噪后的信号光滑性变差。

2)软阈值函数

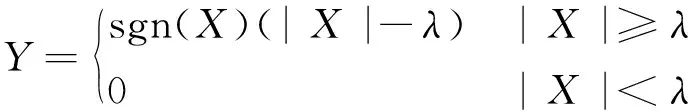
(6)

小波系数经软阈值函数处理后连续性较好，但是当|X|≥λ时，Y与X之间存在一定误差，势必会造成信号重构过程出现偏差。

3)半软阈值函数

函数表达式如下：

(7)

式(3)中，λ1、λ2为给定阈值。

由上式可以看出，当λ1<|X|≤λ2时，接近软阈值函数；当|X|>λ2时，与硬阈值函数相同；当λ1=λ2时，为硬阈值函数；当λ2=时，为软阈值函数。

2.2 EEMD与半软阈值联合降噪

本文将EEMD与小波半软阈值函数相结合，对振动信号做降噪处理，利用EEMD将原信号分解为若干IMF分量，通过小波半软阈值函数对各个IMF分量进行降噪处理，最后将降噪后的各个IMF分量重构，步骤如下：

1)原信号x(t)经EEMD分解为若干个IMF分量；

2)对各个IMF分量做多尺度小波分解，得到各尺度的细节系数以及近似系数，确定阈值规则，计算各层细节系数的阈值；

3)利用小波半软阈值函数，对各层细节系数做降噪处理，重构得到降噪后的IMF分量；

4)将降噪后的IMF分量重构得到降噪后的信号。

(8)

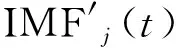
本文提出EEMD与小波半软阈值联合降噪的方法并验证其有效性。

3 仿真与实验

3.1 不同阈值函数降噪效果仿真

为验证基于EEMD的小波半软阈值函数的降噪效果，构造一个轴承振动仿真信号，表达式如下：

s=sin(2πf1t)(1+0.1sin(2πf2t))

(9)

式(9)中,f1为与故障相关的特征频率，f1=100 Hz；f2为轴转速频率，f2=10 Hz。

原始信号s与带噪信号s′的波形图如图1所示。

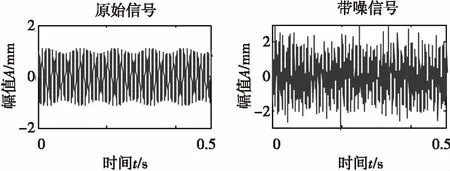
图1 原始信号与带噪信号Fig.1 Original and noise corrupted signal

文献[8]已验证小波半软阈值降噪算法优于软、硬阈值降噪算法，故本文仅选取半软阈值算法与其余几种算法进行比较，对于软、硬阈值降噪算法将不做赘述。分别用EEMD降噪法、小波半软阈值降噪法、基于EMD的小波软阈值、硬阈值降噪法和基于EEMD小波半软阈值降噪法对信噪比为4.635 7 dB的带噪信号做降噪处理。小波函数选取为sym8小波，分解层数选择5层，选取rigrsure规则作阈值规则[16]，得到降噪效果时域图，如图2所示，图(a)—(e)分别代表上述五种降噪算法对含噪信号降噪处理后得到的效果图。通过对比分析可知，图2(e)中的毛刺得到了很好的抑制，基于EEMD的小波半软阈值降噪法最大程度上复原了原始信号。

评价降噪性能的指标主要有均方根误差(Root Mean Square Error,RMSE)和信噪比(Signal to Noise Ratio,SNR)，其表达式分别为式(10)、式(11)。

(10)

(11)

式(10)、式(11)中，x(t)为原信号，x′(t)为经过小波阈值降噪的信号，N为采样点个数。

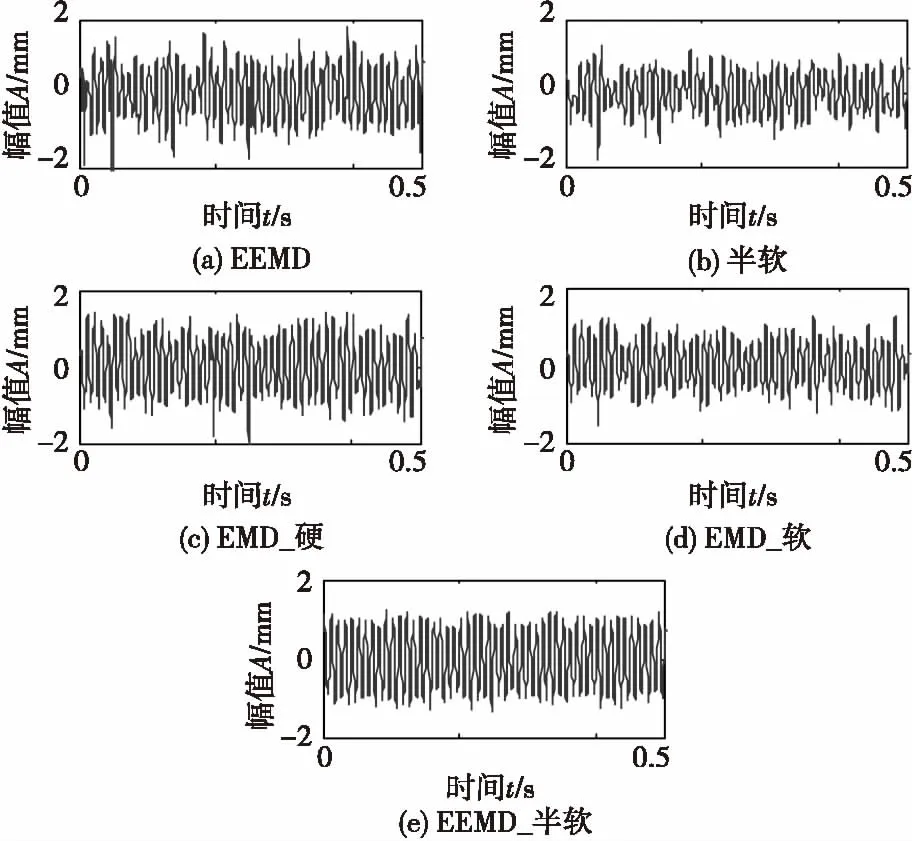
图2 时域图Fig.2 Time domain graph

RMSE数值越小，表示降噪效果越好，与之相反，SNR数值越大表示降噪效果越好。表1中给出了不同阈值函数降噪后的均方根误差与信噪比，由表1可知，本文算法的RMSE为最小值0.211 7 V，SNR为最大值10.497 7 dB。因此，基于EEMD的小波半软阈值法降噪效果优于另外几种方法的降噪效果，其更好地减少了噪声干扰，使得降噪后的信号更接近于原信号。

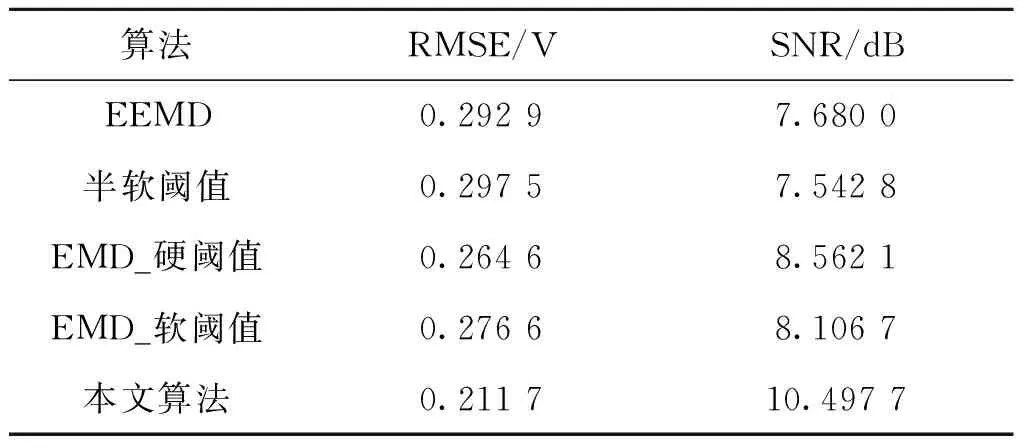
表1 降噪效果对比Tab.1 Denoising effect contrast

将时域图转化为频域图，如图3所示，图(a)、图(b)分别为原信号和带噪信号频域图，图(c)—(g)分别为各算法降噪后的信号频谱图。由图(c)—(g)可以看出，上述五种降噪法得到的特征频率分别为100.3 Hz，100.5 Hz，99.7 Hz，99.6 Hz，100.2 Hz，与原始信号的特征频率100 Hz接近。由图3(g)可知，基于EEMD的小波半软阈值降噪法能够更好地抑制高频部分的噪声信号，同时提高了低频部分边频带的调制频率分辨率，能够有效保留低频部分的细节信息，证明本文算法降噪效果最好，并且能较好地复原信号。

图3 频域图Fig.3 Frequency domain graph

3.2 实验信号降噪

实验数据选自于美国西储大学轴承数据中心。本文选取试验台中支撑电机转动轴的深沟球轴承，型号为6205-2RS SKF，其规格参数如表2所示。

本文选取的数据中电机转速为1 797 r/min，采样频率为12 kHz，采用电火花技术在轴承外圈加工单点损伤，损伤直径为0.177 8 mm。依据轴承参数与电机转速计算出轴承外圈故障特征频率为107.4 Hz。选取外圈故障信号的2 000个点用于验证本文提出的降噪方法。图4(a)为采集的外圈故障特征的观测信号，对采集的信号进行包络谱分析，得到的包络图如图4(b)所示，其中108 Hz与理论上轴承外圈故障特征频率107.4 Hz很接近，216 Hz对应轴承外圈故障特征频率的二倍频。

表2 62052RS SKF轴承参数Tab.2 Parameters of 6205-2RS SKF bearing

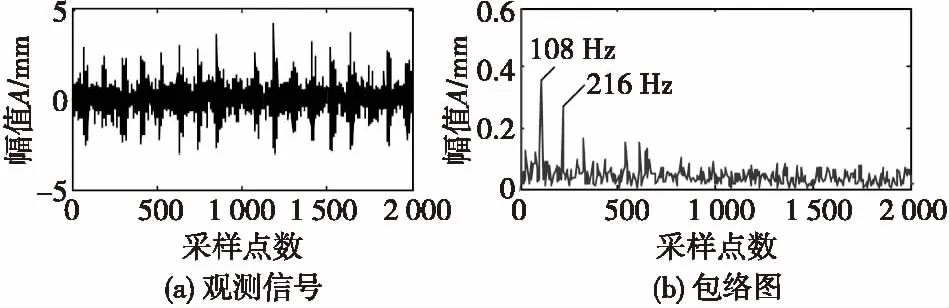
图4 采集的观测信号Fig.4 Collection of observed signal

分别利用以上五种降噪法对采集的振动信号做降噪处理，处理结果如图5所示。

图5 降噪效果对比Fig.5 Denoising effect contrast

图5(a)—(e)分别对应五种方法降噪后的时域图与包络图，五个包络图显示出轴承的故障特征频率分别为106.2 Hz，108.4 Hz，106.3 Hz，108.3 Hz，108.7 Hz，与理论上轴承故障特征频率107.4 Hz相近，且五种方法降噪后的信号也清楚显示出故障特征频率的二倍频。由时域图对比可以看出，基于EEMD的半软阈值降噪法相较于其他四种算法最大程度地抑制了信号中的毛刺，保留信号中的有用信息。在频域图中可以看出，该降噪算法很好地抑制了故障特征频率的边带频。图5(g)与(e)均显示出故障特征频率的二、三倍频，相比较之下，图5(g)二、三倍频凸显效果更优，且四、五、六倍频也可以清晰显示。综上所述，基于EEMD的小波半软阈值函数能够最大限度的抑制信号中的噪声，并且在重构过程中能最大限度的复原信号的有用信息，具有良好的降噪效果。

4 结论

本文提出了基于集合经验模态的小波半软阈值降噪方法，该方法在一定程度上避免了EMD分解过程中出现混叠的现象，且降低了重构信号的偏差，对信号降噪的同时能更准确地将信号波形复原。仿真及实验结果表明，基于EEMD的小波半软阈值降噪方法具备两种方法的优点，相较于本文中另外几种算法，该算法能够很好地抑制信号中的噪声，在重构过程中能较好地复原信号的有用信息，且该方法在机械振动信号降噪方面具有良好的降噪性能。仿真和实验结果验证了基于EEMD的小波半软阈值降噪方法的有效性。