基于高阶球面-径向准则的多传感器融合算法

余战秋

(安徽工业经济职业技术学院计算机科学技术系，安徽 合肥 230000)

0 引言

多传感器融合在军事领域的海洋监视系统和军事防御系统，民事领域的智能处理和工业化控制等方面都有广泛应用[1-2]。根据传感器之间连接方式不同，多传感器融合主要包括集中式多传感器融合和分布式多传感器融合两种方式。

对于集中式多传感器融合，与扩展卡尔曼滤波(Extended Kalman Filter, EKF)[3-4]具有相同框架的扩展信息滤波(Extended Information Filter, EIF)通过对信息贡献向量和信息贡献矩阵求和的方式解决多传感器融合问题。文献[5—6]提出不敏信息滤波(Unscented Information Filter, UIF)，提高了多传感器信息融合的精度。文献[7—11]将三阶球面-径向准则引入信息滤波中，提出容积信息滤波(Cubature Information Filter, CIF)和均方根容积信息滤波(Square-root Cubature Information Filter, SCIF)，获取了更高的融合精度。

对于分布式多传感器融合，文献[13—15]采用平均一致性滤波器，对多传感器信息进行融合，应用集中式滤波算法对融合结果滤波，提出分布式容积信息滤波(Distributed Cubature Information Filter, DCIF)、分布式均方根容积信息滤波(Distributed Square-root Cubature Information Filter, DSCIF)以及分布式五阶容积信息滤波(Distributed Fifth-degree Cubature Information Filter, D5thCIF)，有效处理分布式多传感器信息融合问题。文献[16]基于七阶球面-径向准则提出七阶容积卡尔曼滤波(Seventh--degree Cubature Kalman Filter, 7thCKF)，能够获取比三阶和五阶算法更高的滤波精度，可将其扩展至多传感器融合领域，以进一步提高多传感器融合精度。本文针对此问题，提出了基于高阶球面-径向准则的多传感器融合算法。

1 高阶球面-径向准则

1.1 系统模型

考虑离散非线性动态系统为：

(1)

式(1)中，xk∈Rn为n维状态向量，zk∈Rm为m维量测向量。wk和vk为相互独立的系统噪声和量测噪声，二者为零均值的高斯白噪声，噪声协方差分别为Qk和Rk。

1.2 七阶球面-径向准则

文献[16]提出的七阶球面-径向准则，可获得比三阶和五阶更高的近似精度，进一步提高非线性系统状态估计精度。

对于函数积分的近似，七阶球面-径向准则表示为：

(2)

式(2)中：

(3)

(4)

(5)

(6)

(7)

(8)

(9)

式(2)中各子部分可以表达为：

(10)

(11)

{g1}表示从g1中采样，式(10)和式(11)都包括2n个采样点，el表示单位矩阵第l列。

(12)

(13)

{g2}表示从g2中采样，包括点集{m1}、{m2}、{m3}和{m4}，分别表示：

(14)

(15)

(16)

(17)

(18)

(19)

{g3}表示从g3中采样，包括点集{m5}、{m6}、{m7}和{m8}，分别表示：

(20)

(21)

(22)

(23)

2 高阶球面-径向准则的多传感器融合算法

2.1 C7thCIF算法

七阶球面-径向准则采用更多采样点拟合函数高斯加权积分，具有比三阶、五阶准则更高的拟合精度，将七阶球面-径向准则嵌入信息滤波器框架，提出能够处理集中式多传感器信息融合的C7thCIF算法。

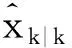
Pk|k=Sk|k(Sk|k)T

(24)

计算容积点xi,k|k：

(25)

其中，εi即式(10)到式(23)的采样规则。计算时间更新：

(26)

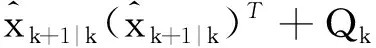
(27)

其中，wi即式(3)到式(9)的权重。有：

Yk+1|k=(Pk+1|k)-1

(28)

(29)

Pk+1|k=Sk+1|k(Sk+1|k)T

(30)

(31)

(32)

(33)

(34)

Ik+1=Yk+1|kPxz,k+1|k(Rk+1)-1(Pxz,k+1|k)T(Yk+1|k)T

(35)

(36)

Yk+1|k+1=Yk+1|k+Ik+1

(37)

(38)

Pk+1|k+1=(Yk+1|k+1)-1

(39)

(40)

(41)

通过式(40)和式(41)，C7thCIF能有效处理集中式多传感器信息融合。

2.2 D7thCIF算法

采用平均一致性算法对多传感器信息进行处理，并采用C7thCIF对平均一致值进行滤波，提出D7thCIF，有效处理分布式多传感器信息融合问题。

使用无向图G=(V,E)对传感器间无线通信网络进行建模，其中，V={1,2,…,J}为传感器集合，J为传感器个数。E={(i,j),i,j∈V}为通信链路集合，如果i和j之间可以通信，则(i,j)∈E，此时传感器i和j称为邻居。如果无向图中任意两个节点之间存在一条路径，则称该图是连通的。平均一致性算法定义了邻居节点间信息交互的规则，网络中每个节点的状态在该规则的作用下不断趋于平均值。策略为：

(42)

式(42)中，Ψi(t)、Ψj(t)为节点i、j的状态，t为一致性迭代次数，λi,j(t)为加权系数。假设节点i的初始状态为Ψi(0)，无向图是连通，所有节点在规则下收敛于初始值的平均值。即：

(43)

定义平均逆协方差矩阵和平均量测矢量：

(44)

(45)

式(36)和式(37)变为：

(46)

Yk+1|k+1=Yk+1|k+nMk+1

(47)

令：

(48)

(49)

通过式(48)和式(49)，集中式滤波可通过传感器间的信息交互分布式实现，处理分布式多传感器信息融合。

3 实验分析

3.1 集中式多传感器信息融合对比

实验的软硬件环境设置为：Microsoft Windows 10系统，Matlab2014.a软件，2.2 GHz处理器，内存为4 GHz。

以三维空间中目标跟踪为例进行说明，定义状态向量[xk,vx,k,yk,vy,k,zk,vz,k]T，状态方程为：

定义量测向量[L,α]T，对于不同位置传感器[xs,ys,zs]T，量测方程为：

目标初始状态[5 000，-100,10 000，-200,200,100]T，采样间隔T=1 s，运动时间为50 s，过程噪声协方差：Qk=diag([80,10,80,10,80,10])；初始协方差：P0=diag([1 000,100,1 000,100,1 000,100])。

分别有四部传感器获取目标量测，位置分别为：A坐标[0,0,0]，B坐标[10 000,0,0]，C坐标[0,10 000,0]，D坐标[10 000,10 000,0]，在集中式多传感器信息融合对比中，采用传感器A作为融合中心，其他传感器信息传送到A进行融合。四个传感器量测噪声协方差分别为：

对比算法为三阶、五阶球面-径向准则的集中式多传感器信息融合算法CCIF、C5thCIF。对位置和速度的RMSE对比如图1所示。

图1 集中式多传感器融合算法RMSE对比Fig.1 The comparison of RMSE in centralized multi-sensor fusion algorithm

综合图1(a)位置RMSE对比结果和图1(b)的速度RMSE对比结果，可以看出，三种基于球面-径向准则的算法，由于在信息滤波框架下，都能够实现多传感信息融合问题。同时可以看出，本文提出的C7thCIF算法具有最高的融合精度，五阶算法次之，三阶算法最低，这是由于采用不同阶数的球面-径向准则，对于函数积分的近似效果不同，五阶球面-径向准则优于三阶，七阶准则采用更多的采样点，近似效果最好。

3.2 分布式多传感器信息融合对比

考虑2.1节中相同的系统，四个传感器为分布式，传感器之间的拓扑结构如图2所示。

图2 多传感器拓扑结构Fig.2 The topological structure of multiple sensors

与集中式多传感器信息融合问题相同，在此对比算法为三阶、五阶球面-径向准则的分布式多传感器信息融合算法DCIF、D5thCIF。对位置和速度的RMSE对比如图3所示。

图3 分布式多传感器融合位置RMSE对比Fig.3 The comparison of RMSE in distributed multi-sensor fusion algorithm

综合图3(a)分布式多传感器位置RMSE结果和图3(b)分布式多传感器速度RMSE结果，可以看出，通过平均一致性算方法对集中式多传感器量测进行处理后，采用集中式滤波算法滤波，可有效处理分布式多传感器融合问题。从融合精度方面看，D5thCIF的精度高于DCIF，D7thCIF的融合精度最高，这与三种算法采用的球面-径向准则不同有关。D7thCIF采用七阶球面-径向准则，采用最多的采样点拟合函数积分，能够获取更好的近似精度。

所提多传感器融合算法基于七阶球面-径向准则，融合精度高于三阶、五阶算法的同时，采样点多于二者，计算复杂度增加，其对比如表1所示。

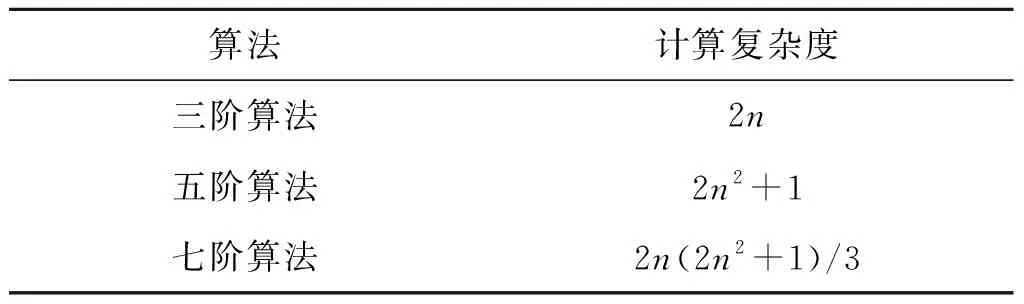
表1 算法计算复杂度对比Tab.1 Comparison of computational complexity

4 结论

本文提出了基于高阶球面-径向准则的多传感器融合算法。该算法将七阶球面-径向准则嵌入信息滤波框架，提出能够处理集中式多传感融合的C7thCIF算法；然后，采用平均一致性算法对多传感器信息进行处理，采用C7thCIF对平均一致值进行滤波，推导了能够处理分布式多传感器融合的D7thCIF算法，提高了集中式和分布式多传感器融合的精度。仿真结果表明，高阶算法能够获取比低阶算法更好的融合精度，但增加了计算复杂度。