基于对偶双环滑模的空间翻滚目标相对绕飞控制

郝宇星，申 麟，李 扬

（中国运载火箭技术研究院研究发展中心，北京，100076）

0 引 言

空间故障或失效航天器、太空碎片、空间星体等在轨目标是重要的一类在轨服务对象，在进行对接、维修、抓捕、观测等任务时，目标的翻滚给工作带来很大的难度。与传统的空间飞行器位姿跟踪控制不同的是，在空间翻滚目标的捕获任务中，由于目标的非合作性，无法获得精确的位置姿态测量信息，如果直接对不精确的估计位姿进行跟踪，势必对航天器的跟踪精度造成影响。其次，在空间翻滚目标抓捕的过程中，航天器与非合作目标之间保持相对超近距离运动，航天器与非合作目标间的相对位置和相对姿态互为耦合，使得空间操作的安全性受到威胁，姿态和轨道控制需要同时考虑，从而间接地对其控制系统提出更高的要求。近年来的相关研究都围绕翻滚目标的特性与耦合控制来进行。刘宗明等[1]为空间翻滚目标相对姿态的精确测量，提出了基于数据库的非合作目标检测策略；郭永等[2]针对非合作的失控航天器，利用蔓叶线建立了避障模型，并使用滑模控制方法进行交会对接的姿轨耦合控制；刘欢等[4]针对空间碎片的抓捕问题，使用轨道根数法与C-W方程分别设计了绕飞轨道，但未考虑二者的姿态影响。本文将建立位姿一体化描述的相对动力学模型，并使用以对偶数为变量的双环滑模控制方法进行相对空间翻滚目标的绕飞控制。

1 旋量、对偶四元数的表示和运算

三维刚体运动有3个平移自由度和3个旋转自由度，因此可将六维空间的向量称为一个旋量，映射一个三维刚体运动。几何上用六维列向量表示，代数上可用对偶数表示，形式如下：

式中 ε为对偶单位，其性质为0ε≠，20ε=；α，α′分别为主部和副部，或称为实部和对偶部，在表示物理量时，主部表示平移相关的量，副部表示旋转相关的量。对偶数在旋量几何中表示旋量的运动，也可以表示坐标系的平移和旋转。其形式为

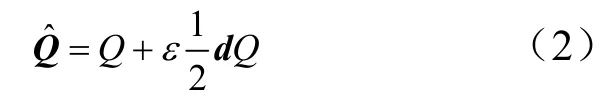
式中 d为平移向量；Q为四元数。对偶四元数可看作主部与副部均为四元数的对偶数，矩阵运算中表示为八维列向量。

a）对偶四元数积。

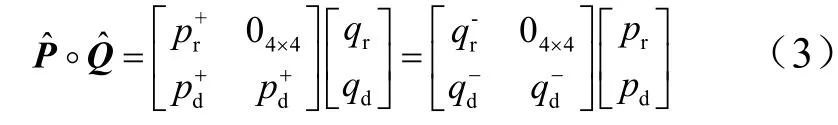
式中 四元数积用·表示；下标：r为对偶四元数的主部，d为对偶四元数的副部。

四元数乘法的矩阵运算为

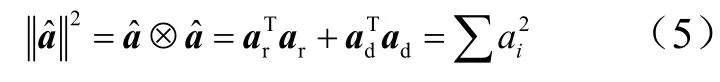
c）对偶互补算子。

d）对偶数叉乘用×表示，其矩阵运算为

2 航天器位姿耦合动力学模型

坐标原点位于地心iO，OiXi轴在赤道面内指向春分点方向，iiOZ轴指向地球自转角速度方向，iiOY轴与其余两轴构成右手正交坐标系。

坐标系定义：

坐标系原点位于航天器的质心，3个坐标轴的方向分别与航天器的惯性主轴重合。追踪航天器及其本体坐标系用P表示，目标航天器及其本体坐标系用C表示，惯性系用i表示，如图1所示。

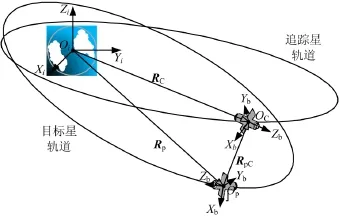
图1 航天器在轨相对运动模型Fig.1 Spacecrafts’ Relative Motion Model

追踪器P相对的对偶四元数为

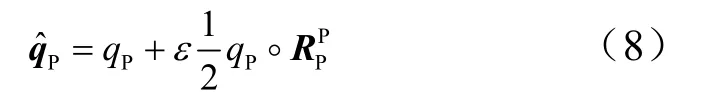
目标器C相对惯性系i的对偶四元数为

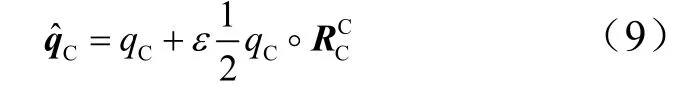
式（8）、（9）表达了P，C坐标系与惯性系的转换关系，并将式（8）、（9）对时间进行微分，得：

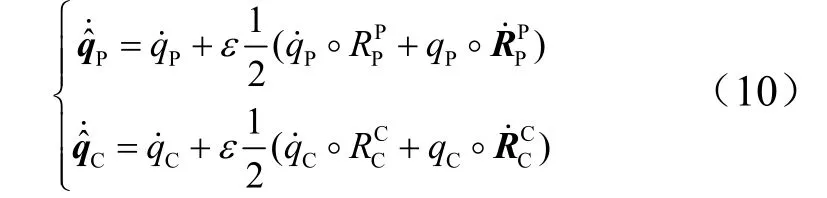
由四元数乘法性质：

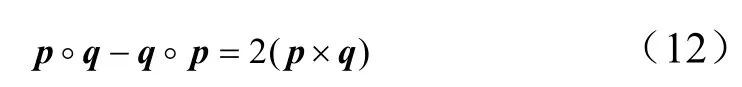
其中，q与p为四元数的矢量部分，可得：

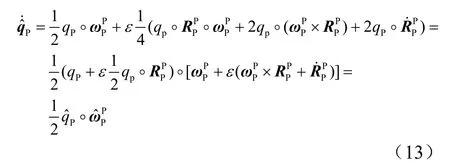
以及：

式（13）与（14）即为追踪器P与目标器C在各自本体坐标系下的运动方程。其中PPˆω与CCˆω同时包含了航天器的轨道与姿态运动信息。

为了描述追踪器与目标器之间的相对运动，定义相对运动对偶四元数为

记追踪器P相对目标器C的位置向量为PCR ，表示在C本体坐标系下即，有：

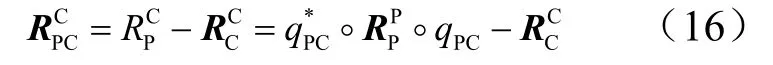
将式（15）展开得：

类似地，有：

式（18）的相对位置矢量表示在追踪本体系中，便于计算控制力。

对式（17）两边微分，得：

定义：

为追踪器P相对目标器C的速度对偶数在C的本体坐标系下的表示，则有：

对式（20）求导得：

在各自本体坐标系下，航天器P与C的动力学方程为

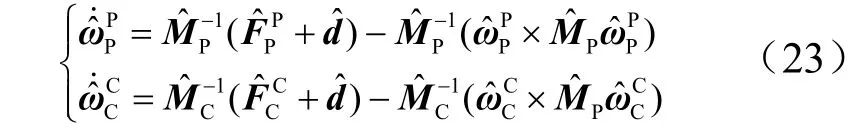
代入式（18），得到：

式（23）在目标器本体系下表示的航天器相对动力学方程。

3 相对翻滚目标绕飞的位姿耦合控制

3.1 航天器相对绕飞设计方法

以设计相对速度旋量为目标时，根据式（15），得：

由式（13）、式（15）得：

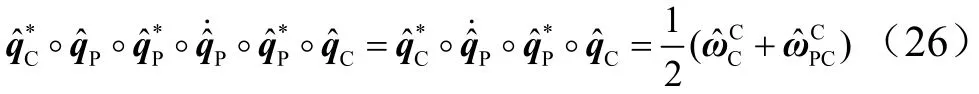
则：

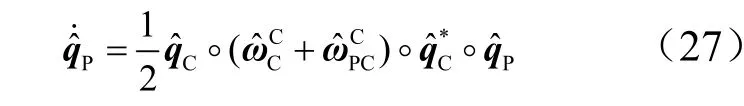
在以绕飞轨迹为目标的任务中，根据式（15）得：

3.2 基于对偶数的双环滑模控制

双环滑模控制在飞行器控制领域，特别是四旋翼飞行器以及直升机姿态控制领域得到较多的应用，具有实现简单、与模型结合紧密的特点。本节在以对偶数为控制变量的条件下，采用双环滑模变结构控制方法设计航天器控制器，使积分滑模来实现切换函数的设计。外环滑模控制率实现对位姿信息的跟踪，外环控制器产生对偶速度指令，并传递给内环系统，内环则通过滑模控制率实现对指令的跟踪。目标器与追踪器采用同一动力学模型，翻滚目标的运动信息由模型解算并输出到相对位姿计算模块，由给定的绕飞条件得到追踪器的位姿对偶四元数指令Cˆq。系统结构如图2所示。

图2 控制器系统结构Fig.2 Controller System Structure

a）外环滑模控制。

定义对偶四元数跟踪指令偏差为

设计积分滑模面为

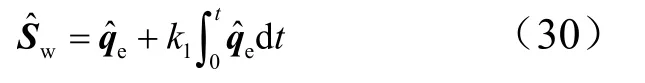
式中1k为增益，10k＞ ，通过选择合适的1k可以使系统的跟踪误差在一个比较理想的滑模面上滑动至稳定。

则：

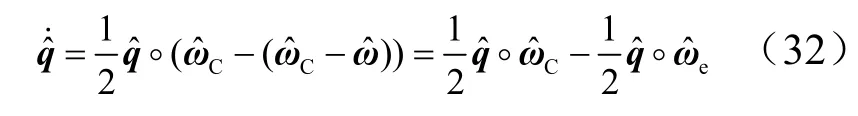
对滑模面求导得：

设计对偶速度指令为

式中1ρ为常数，10ρ＞。取如下Lyapunov函数：

b）内环滑模控制。

内环积分滑模面取为

式中2k为增益，20k＞ 。

则：

设计内环控制率为

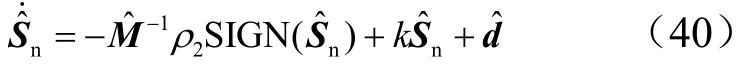
取如下Lyapunov函数：

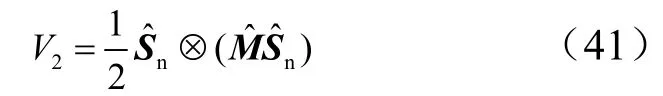
则：

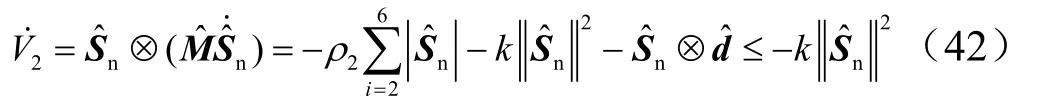
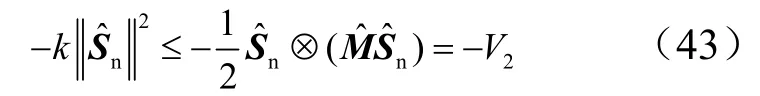
即：

因此2V指数收敛，且当内环收敛速度大于外环收敛速度时，总控制系统稳定。

传统的滑模控制使用了符号函数sgn()s来保证状态量在滑模面附近运动。当系统的轨迹到达切换面时，其速度是有限大，惯性使运动点穿越切换面，从而最终形成抖振，叠加在理想的滑动模态上。一种常见的解决办法是使用饱和函数sat()s代替理想滑动模态中的符号函数sgn()s，即：

3.3 相对绕飞任务设计

任务对象为近地轨道运行的航天器，由于姿控系统失效在轨道上作翻滚运动[5～7]。因此，追踪航天器当前任务为在较近的距离下对目标航天器进行目标本体系下的绕飞，保证姿态对准，为其他任务（交会对接）做准备[8～12]。具体数据如表1所示。

表1 绕飞任务数据Tab.1 Flying Around Mission Data

绕飞目标航天器以美国1973年发射的天空实验室（Skylab）为参考，作为美国的第1座空间站，在发射过程中曾因碰撞导致部分太阳帆板未能展开，美国随后发射了维修航天器与之对接，解决了这一问题。对比近年来各国发射的载人飞船与货运飞船，质量均在10 t以上，考虑到未来大型航天器逐渐增多，以此类航天器作为研究对象具有应用价值[13,14]。

失控大型航天器在进行翻滚过程中，姿态不断变化，为保证接口对准，在进行相对绕飞时，相对姿态应保持不变[15～17]。与此同时二者维持一定的绕飞距离，如图3所示。本任务使用设计ˆPCq 的方法。

图3 航天器相对位姿示意Fig.3 Space Crafts’ Relative Position

3.4 仿真校验

校验使用数学仿真。由于对偶数模型主部与对偶部相互作用，但数量级偏差很大（310级），属于刚性系统，故微分方程解法使用 ODE15s法，取系统自动步长，可以获得较快的计算速度。

目标航天器与追踪航天器应用相同的干扰模型，均为常值干扰加速度与周期性干扰力矩，不考虑J2项影响。控制参数取图4～7为追踪航天器的对偶四元数与对偶速度跟踪预定值的效果，可以看出：内外环跟踪误差均在短时间内收敛到零附近，在60 s的任务期间保持跟踪预定信号效果良好。其中外环姿态四元数收敛时间在0.4 s左右，位置四元数收敛时间为0.8 s；内环角速度收敛时间为0.2 s左右，内环速度收敛时间为0.6 s。内环的收敛速度比外环快0.2 s，在内环快速收敛的条件下，保证了外环的快速收敛。

图4 相对姿态四元数Fig.4 Relative Attitude Quaternion

图5 相对位置四元数Fig.5 Relative Location Quaternion

图6 虚拟控制角速度Fig.6 Virtual Control of Angular Velocity

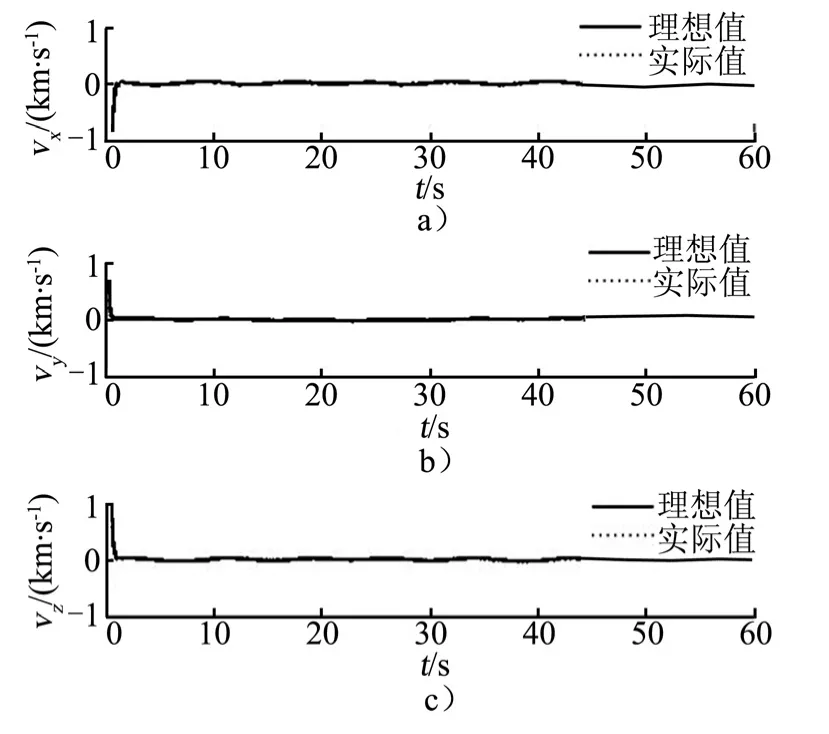
图7 虚拟控制线速度Fig.7 Virtual Control of Velocity

目标器与追踪器在地心惯性系下的轨道运动，目标器沿圆轨道运行，追踪器在圆轨道的基础上作相对绕飞运动，如图8所示。将两航天器的位置矢量差，即相对位置矢量投影在地心惯性系中，如图9所示，可看出轨迹为三维空间中周期性进动的圆弧，说明追踪器在进行绕飞的同时受到了目标器的姿态进动影响。目标航天器的转动可分为自旋与进动，如图10所示，x方向的角速度保持在0.33 rad/s，章动在与Oyz平行的平面，幅度为0.3 rad/s，这样的姿态变化一方面造成了追踪航天器绕飞平面的变化，也使追踪器不断调整姿态来对准目标器。

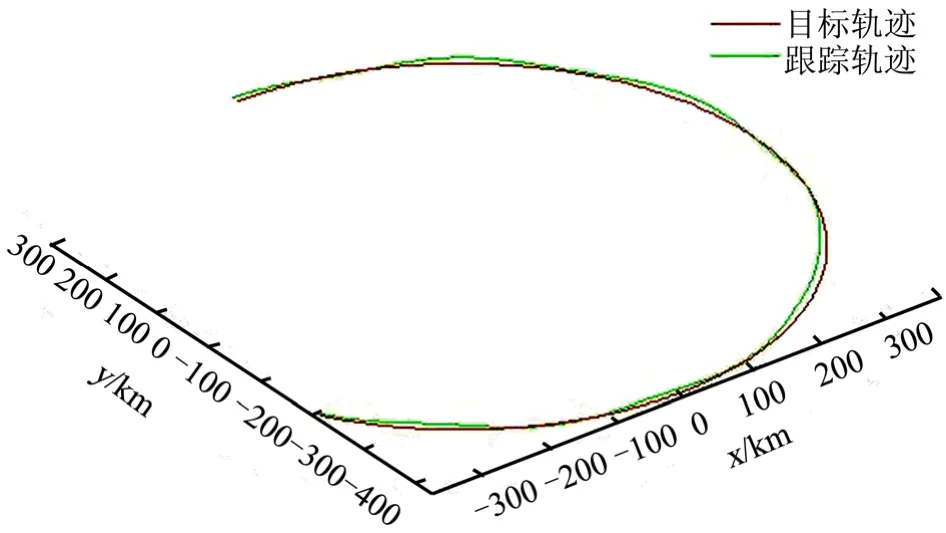
图8 目标器与追踪器轨道运动Fig.8 Target and Chaser’s Orbital Motion

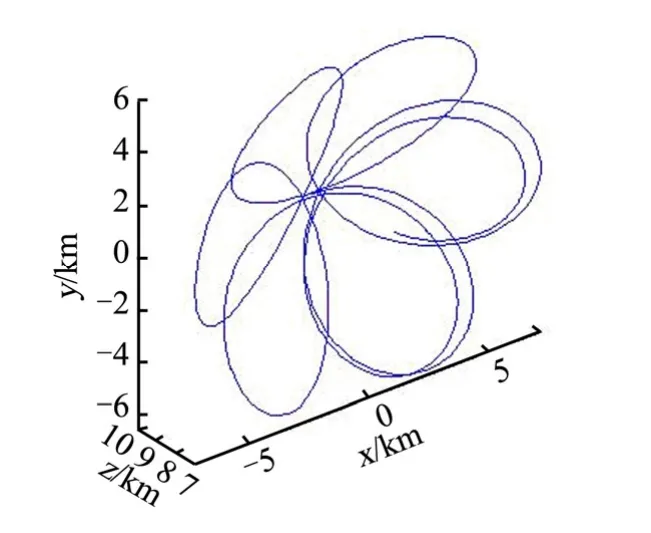
图9 目标器与追踪器相对位置矢量Fig.9 Target and Chaser’s Relative Position Vector

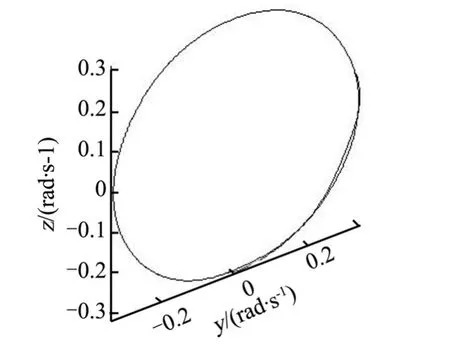
图10 目标航天器角速度矢径Fig.10 Target’s Palstance Vector Track

追踪器控制加速度变化曲线如图11所示。由图11可知，追踪器控制加速度在200～2000 m/s、角加速度在5000～50 000 rad/s2之间，说明大质量、大惯性矩航天器在位姿的控制上需要更大的控制能力，对绕飞任务推力设备提出了较高的要求。

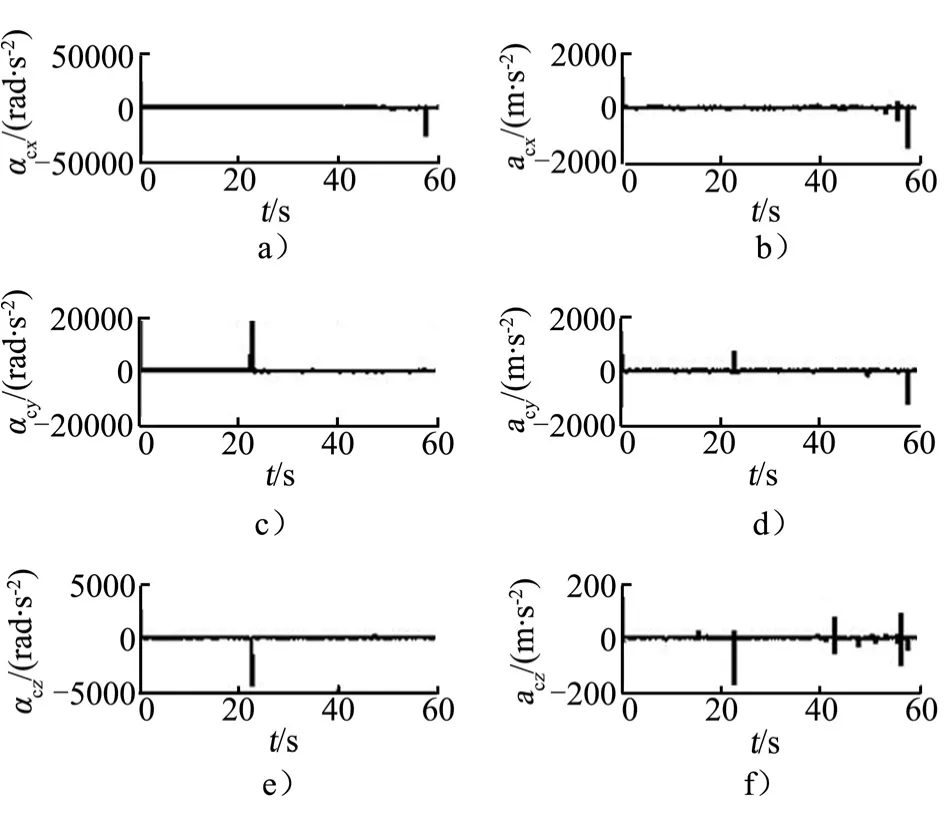
图11 追踪器控制加速度变化Fig.11 Chaser’s Controlling Acceleration

绕飞任务要求追踪器与目标器保持10 km的距离，追踪器距离保持偏差如图12所示。由图12可知，两航天器预定距离的负向偏差最大为1 km，此时两航天器距离9 km，属于安全范围，且在较长时间内距离偏差保持在200 m以内。

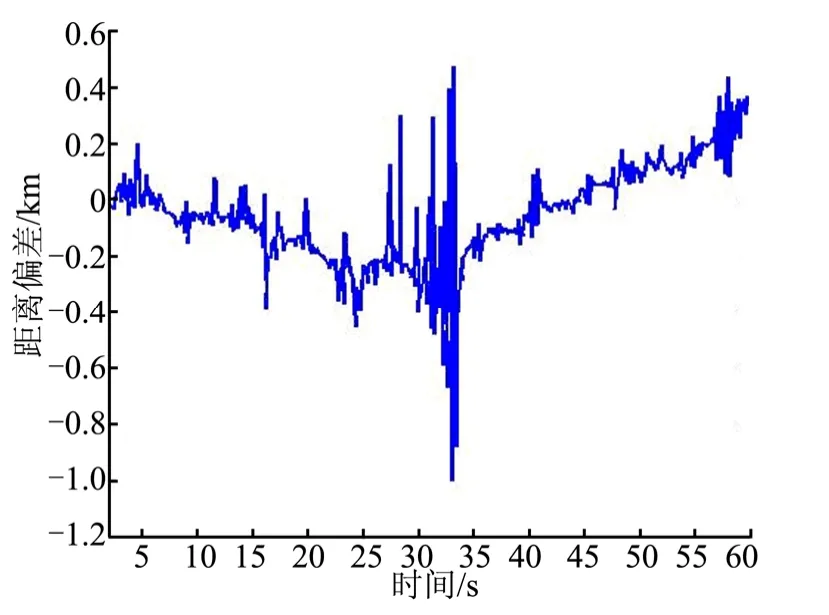
图12 追踪器距离保持偏差Fig.12 Target and Chaser’s Distance Deviation

4 结 论

本文针对空间翻滚目标的动力学问题，引入对偶四元数与旋量概念，建立位姿一体化的翻滚航天器的动力学与相对运动学模型，并提出两种绕飞轨道设计方法。以近地大型翻滚航天器的相对绕飞为例，设计了姿轨耦合的滑模控制器，仿真结果表明，基于对偶数的双环滑模控制系统可以快速有效地控制追踪航天器的位姿，并在翻滚目标角速度变化的同时保证二者的姿态同步与距离稳定。