面向大型载人航天器的系统健康状态评估方法研究

陈润锋，杨 宏

（中国空间技术研究院载人航天总体部，北京100094）

1 引言

可靠性和安全性一直是航天工业中关注的重点问题，特别是载人航天领域。随着载人航天活动的不断拓宽，航天器性能不断提高，系统的规模也越来越大、越来越复杂，系统发生故障／异常的可能性就越高，传统依靠产品自身的可靠性，以及设计冗余备份的方法不足以确保系统的长期安全运行。

健康状态是表征系统可靠性和安全性的重要指标，实时地掌控载人航天器系统的健康状态愈发重要。健康状态是指研究对象在完成其设计功能时的执行能力，一般可以描述为正常（健康）、异常（非健康）、以及异常情况下不同程度的性能下降（偏离健康的程度）［1］。目前，健康状态评估方法主要分成两类：经典的评估方法和基于人工智能的评估方法。经典的评估方法包含有层次分析法（Analytic Hierarchy Process， AHP）［2］、模糊理论（Fuzzy Theory）［3］和 D-S 证据理论（D-S evidence theory）［4］等。 瞿红春［5］使用 AHP 对发动机的健康状态进行了评估，建立振动监测、滑耗监测、返厂维修等12个数据指标，并将最终权值相加的结果映射至［0，1］区间，作为发动机的健康指数。Abdullayev等［6］针对燃气涡轮发动机状态数据的不确定性，运用模糊理论建立了多线性和非线性描述模型来评价发动机的健康状态。Liu B J等人［7］对液压系统的工作状态进行分类，利用D-S理论进行健康状态评估，使用熵值法来确定证据理论中的权重。这类方法的基本思想是建立评价指标体系，计算指标权重，对所有指标进行权值相加，得到最终评价结果。人工智能的评估方法主要包含人工神经网络（Artificial Neural Networks， ANN）［8］、支持向量机（Support Vector Machine， SVM）［9］和贝叶斯估计理论（Bayesian estimation theory）［10］。 Gao R X 等［11］以故障严重度为指标对轴承的健康状态进行分类，利用小波变换提取出轴承振动数据特征量，用以训练神经网络模型，实现对轴承健康状态的判别功能。Huang H Z等人［12］利用SVM对轴承、电池的当前状态进行评估，并建立了当前状态与剩余寿命之间的联系。孙见忠［13］提出了基于贝叶斯因子的民航发动机气路部件性能评估的方法，并以发动机的排气温度裕度作为退化参数，建立了性能退化轨迹。这类方法主要是建立类似于人的学习和判断模型，其中ANN和SVM主要通过对训练样本进行学习，建立起数据特征到健康状态的映射模型，是一种“黑箱建模”的思想；贝叶斯方法首先建立研究对象随时间变化的状态空间模型，根据观测数据来估计模型参数，以此作为对健康状态的评估。

可以看出，目前研究成果的对象集中于一些具有重要功能的设备，然而，对于工业领域中的复杂系统，相比于单台设备的健康状态，工程中更为关注的是由这些设备组建成的整个系统的健康状态，例如载人航天器中的能源系统，它包含有多个分系统，每一个分系统又是由多种设备构成的，系统层的健康状态则不能简单地用几台核心单机设备的健康状态来代替表述，还需要考虑到设备之间的相互作用关系。目前针对于系统层的健康状态评估研究成果较少，Huang H Z等［14］阐述了系统层健康状态的重要性，并使用模糊层次分析法（Fuzzy Analytic Hierarchy Process，F-AHP）来构建系统层的健康状态，这种方法的本质是一种赋权值而后进行累加的思想，权值能够考虑组成成分的重要性，但这种方法不能很好地描述成分间的相互作用关系。陈雄姿等［15］尝试将系统采集到的多维监测数据统一映射到取值范围为［0，1］的单维虚拟变量上，作为系统健康状态的评估量，这种方法需要具备有大量同类型的历史退化数据进行拟合，而复杂系统的造价通常十分昂贵，很难具备有同种工况条件下的多样本退化数据作为技术支持。

本文以一种典型的大型载人航天器能源系统为研究对象，借助图论和数据科学方法，结合工程中实际资源条件，提出一种新的系统健康状态评估方法，以描述整个系统层的健康状态。

2 系统健康状态评估方法设计

在工业领域中，复杂系统通常包含有大量具有不同功能的单机设备，这些设备通过相互作用共同实现更高层的系统功能，相对于底层单机设备而言，系统层的功能特点是各项单机功能以及其相互作用产生效能的集成。因此，评估整个系统层的健康状态，不仅需要考虑各个单机的健康状态，同时也要考虑到单机设备间相互作用的状态信息。复杂系统的拓扑结构通常呈现为网络的形式，图论是一种十分有效的描述网络特性的数学工具，将系统中的设备视为节点，设备间的相互作用关系视为有向边，则复杂系统的结构关系可以通过有向图表示，对系统的健康状态评估进而可以等价为对有向图中各个成分的度量。

2.1 基本概念定义

假设复杂系统S包含有N台单机设备，与其对应的图 G ＝ （V，E），其中点集V ＝ ｛vi，i∈N｝表示系统中的所有设备，边集E ＝ ｛eij，i≠j，i∈N，j∈N｝表示各台设备之间的作用关系，这样复杂系统就可以通过有向图来表示，如图1所示。

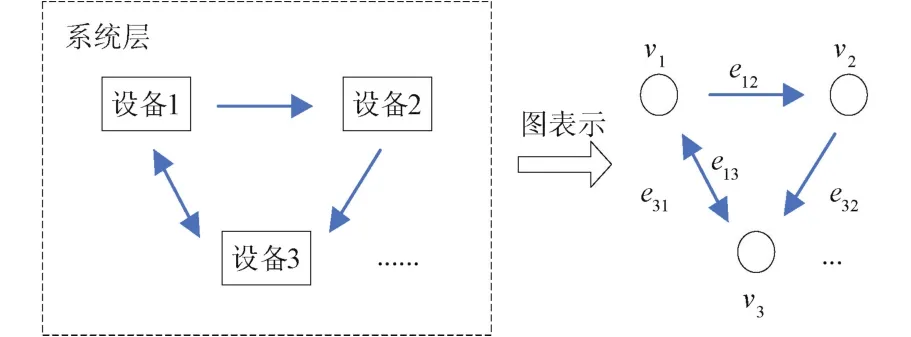
图1 复杂系统的有向图表示Fig.1 Digraph representation of complex system

将复杂系统抽象为有向图，使设备间的相互作用关系更为清晰，以系统层的健康状态为研究目标，对有向图进行度量，包括节点的健康状态和有向边的健康状态两大部分。

2.2 点的健康状态评估

有向图中每一个节点代表单台设备，按照处理数据是否能够直接评估设备健康状态（或退化状态），可以分为直接评估和间接评估两类［16］。直接评估指的是通过经验、机理等先验知识来确认可以直接表征研究对象健康状态的变量，通过直接测量这些变量值以及相关的数值特征，实现对所研究对象健康状态的评估，例如对于热敏感设备，可采用温度变量直接评估设备的健康状态，传统的监测方法会设置门限阈值，若温度越限，则视为设备的健康状态处于异常（非健康），计算温度的均值、方差等统计特征，可以用来评估设备健康状态的趋势和稳定程度等。该类方法框架如图2所示，一般情况下，目标对象有多维度的原始监测数据，从中识别出与健康状态（或退化状态）直接相关的数据变量，随着运行时间呈现出单调下降（或上升）的趋势，此类变量大多数都具有明确的物理含义。

图2 直接评估方法示意图Fig.2 Diagram of direct assessment method

当研究对象的健康状态变量无法直接测量，或者难以通过先验知识辨识出哪些变量可以直接反映健康状态时，就需要间接地去构建系统健康状态评估量。利用研究对象历史测试数据、试验数据、全寿命仿真数据和在线状态监测数据等，结合对象在退化过程中的不同阶段，评价各变量对于研究对象健康状态的影响关系，挖掘数据之间存在的潜在关系，拟合／回归出与研究对象退化趋势相一致的评估量。例如对于机械类系统中的轴承，这种高速转动类设备的健康状态主要取决于结构上的磨损程度，而结构上的损耗、裂纹等变量是无法直接测量到的，需要通过相关的监测数据，进行相应的数据变换，挖掘出与退化过程趋势一致的评估量。由于轴承结构上的磨损会出现不同的振动频率，此时的振动监测数据在幅值上可能仍处于正常范围内，但在频域中出现了与以往正常态相比不同的频率分量，新频率分量与退化趋势一致，则可以作为间接的设备健康状态评估量。这类间接评估量往往没有直接的物理含义，需要借助专家知识进行解释［16］。间接评估方法的架构如图3所示。

图3 间接评估方法示意图Fig.3 Diagram of indirect assessment method

2.3 边的健康状态评估

上述直接评估方法和间接评估方法都是针对单一设备为研究对象，对于复杂系统来说，设备间的相互作用关系也是需要关注的度量对象。本文以有向边的形式表示这种相互作用关系，以图1右侧的有向图为例，有向边e12可以视为节点v1与节点v2间的作用关系，其余边的对应关系详见表1。由于设备间相互作用的机理模型难以准确建立，本文从数据的角度去构建其健康状态评估量。

表1 有向边对应关系Table 1 Relationship of the directed edges

将系统中设备之间的相互作用视为一种能量流的交互，例如电源系统中传递的电流、信息系统中通信的信息流等等，假设这些流在系统正常运行过程中应该遵循特定的动力学模型，当发生故障或异常情况时，视为系统中的流产生了扰动，偏离原本的运动模式。在这种假设的基础上，本文通过描述流的模式来表征有向边的状态，而流的模式是借助于相应监测数据展现出来的，因此对有向边的所有关联数据进行挖掘，发现其中存在的模式特征，通过分析模式的变化来反映状态的变化，进而可以用模式之间的偏差值来评估健康状态。

以节点v1与节点v2间的有向边e12为例，设v1点的观测量记为d1，v2点的观测量为d2，则有向边e12对应的观测量为二维数据集｛d1，d2｝。聚类方法可以挖掘高维数据集中的模式信息，考虑到工业领域中设计的复杂系统属于确定性系统，即系统的输入／输出特性是根据设计功能而定的，数据通常是因果关系型数据。本文采用时域上直接聚类方法，得到数据在空间中聚集的不同区域，将这些区域作为基准模式，然后判断下一观测时刻的数据是否仍然聚集于该区域内，如果落入该区域中，则认为新状态与基准模式对应的状态一致；如果新数据偏离了基准模式对应的区域，则认为存在了某种扰动状态，使得新状态与基准模式相比产生了变化，偏离程度越大，表征状态变化程度越剧烈，如图4所示。

图4 有向边评估方法示意图Fig.4 Diagram of assessment method for the directed edge

这里以航天器能源系统中太阳电池阵和分流调节器为例进行具体展示。太阳电池阵将接收到的光能转变为电能送入分流调节器，分流调节器对产生的电能进行汇聚，并分流掉额外电量，则可以设太阳电池阵为节点v1，分流调节器为节点v2，两者的拓扑关系同上。对于太阳电池阵，选取其电压监测数据作为观测量d1；对于分流调节器，选取其温度监测量作为观测量d2，图5为两个轨道周期的太阳电池阵电压监测数据，图6为对应的分流调节器温度监测数据。从这两幅图中可以看出，由于航天器轨道特性的影响，设备监测数据呈现出周期性变化的模式，单个监测量的数据曲线仅能反映出对应单台设备的监测点状态，建立多监测量之间数据模式上的联系，可以作为反映多设备间相互作用状态的特征量。

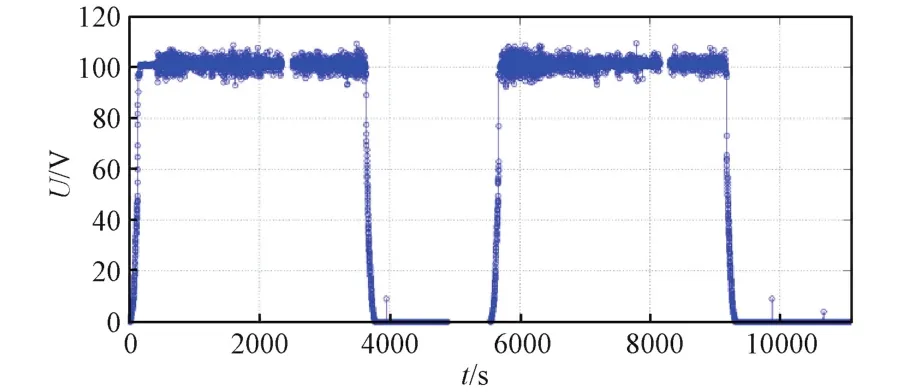
图5 太阳电池阵电压值Fig.5 Voltage of the solar array

图6 分流调节器温度值Fig.6 Temperature of the shunt regulator

对这两组一维数据进行直接聚类处理，绘制其在二维空间内的坐标点，结果如图7所示，可以看出主要分为3类，分别对应航天器入影、阳照／阴影区工作、出影3种工况，这表明聚类处理可以辨识出数据所蕴含的模式特征。

对于二维空间内的度量，设计一种半径为r的圆形探测窗口，计算观测点与探测窗口内包含的检测点的欧式距离d如式（1）所示：

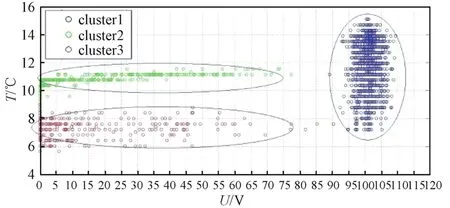
图7 聚类结果示意图Fig.7 Results of clustering

取其中的最小值作为该点的距离值，如图8所示。

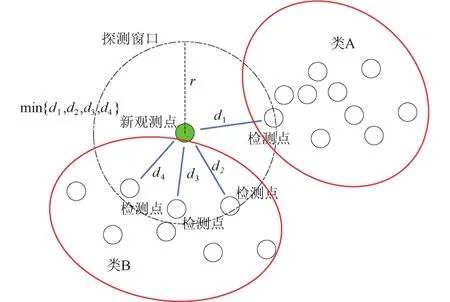
图8 二维空间内点的度量方法示意图Fig.8 Diagram of assessment of point in two-dimensional space

2.4 融合得到系统层健康状态评估量

在对有向图中所有节点与有向边都进行度量之后，系统层的健康状态则是这些度量的融合。设fv和fe分别表征节点和有向边的评估量，HS为系统层健康状态评估量，则有式（2）：

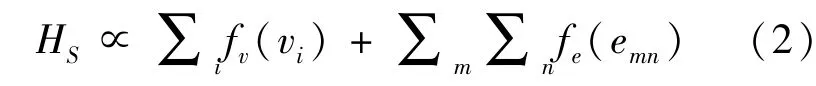
若需要考虑某类设备的重要性时，例如具有多条连接边的节点，或具有重要功能的设备节点，可以通过设置相应权重来表征。

3 应用分析

载人航天器是一种典型的复杂系统，能源系统是其中最为重要的系统之一，它为所有用电设备提供所需要的功率，是保证整个航天器正常运行的关键。为了简化问题，本文将一种典型的载人航天器能源系统作为一个独立的系统进行分析。

目前应用于载人航天器的能源系统均采用太阳电池阵-蓄电池模式，其工作原理是航天器在轨道阳照区时，由太阳电池作为发电装置提供电能，并向蓄电池充电；当航天器进入轨道阴影区时，由蓄电池提供电能。分流调节器设备将多路太阳电池阵产生的电能进行汇聚，并分流掉额外电量。功率管理器实现能源系统的工作逻辑控制，母线控制单元和供电控制单元共同完成对负载设备通断电的控制，如图9所示。

首先将能源系统以有向图的形式表示出来，如图10所示，这里仅考虑单路供电控制单元与负载。节点中标注的数值为该点的度，表示节点连接的边的条数，节点的度可以在一定程度上描述出设备的重要程度。例如节点D3和D10具有较高的度，其代表的分流调节器及功率管理器在能源系统中具有十分重要的作用，与工程实际情况相符。

在建立起系统的有向图模型之后，接下来需要对图中所有的节点和有向边的健康状态进行评估。考虑到构建设备的机理模型较为困难，而航天器在运行过程中会采集得到大量遥测数据，这些数据资源蕴含着对应设备的状态信息。因此本文采用对遥测数据进行处理的方法来评估所有节点和有向边的健康状态。

图9 能源系统示意图Fig.9 Block diagram of the energy system

由于本文可以获取到的在轨遥测数据有限，部分遥测数据并不连续，如图11所示，其中图（a）为太阳电池阵的供电电压，对应节点D1-D2；图（b）为分流调节器的温度，对应节点D3；图（c）为放电调节器的输出电流，对应节点D4-D6；图（d）为放电调节器的温度，对应节点同上；图（e）为电池的充放电电流，对应节点D7-D9；图（f）为母线电压，对应节点D10-D13。

图10 能源系统有向图Fig.10 Digraph of the energy system

图11 可使用遥测数据资源Fig.11 Accessible telemetry data resources

在确定所有可用监测数据之后，对每个节点及每条边的相关监测量进行聚类，绘制其在高维空间中聚集情况，挖掘出存在的模式特征，并将聚类结果整理为矩阵的形式，如图12所示。其中对角线为各节点的处理结果，有向边处理结果的位置与矩阵坐标相一致，例如D1与D3之间的有向边处理结果位于对应的第2行第1列。这里为了简化问题，将节点D1、D2视为同状态，将节点D4、D5、D6视为同状态，将节点 D7、D8、D9视为同状态，矩阵结果是一个下三角阵。

图12 聚类结果示意图Fig.12 Results of data clustering

在得到聚类结果之后，就可以对后续新观测时刻的数据进行分析，判断新观测数据是否落入聚类处理得到的已有模式中。设一个新的监测时间 点 ti， 含 有 13 个 分 量： ［M1（ti），M2（ti），…M13（ti）］，代入公式（1）计算各分量的偏差值，作为对各设备及设备间相互作用的健康状态评估量，结果如图13（a）所示，其中横坐标为时间t，纵坐标为用以度量偏差量的欧式距离值d。最后融合所有分量，得到系统层的健康状态评估量，如图13（b）所示，坐标含义同上。从计算得到的健康状态评估量可以看出，曲线呈现出平稳的趋势，这与数据对应的航天器实际工况相符。可以将这种平稳模式作为系统健康的基准，计算后续观测时刻的模式特征与健康基准之间的偏差量，作为该观测时刻状态偏离健康基准的评估量。由于缺少故障样本数据和性能退化样本数据，这里仅对平稳工况下的航天器能源系统健康状态进行了评估。

图13 系统状态评估结果示意图Fig.13 Results of system health state assessment

4 结论

本文以大型载人航天器对系统高可靠性、高安全性需求为研究背景，围绕健康状态评估方法展开研究，针对实际工程需求，提出了一种新的系统健康状态评估方法：

1）用有向图的形式来描述系统的结构特性，将对系统健康状态评估转化为对有向图各个元素的度量；突出系统中成分之间的相互作用关系，使得最终评估结果能够更完整地体现出系统层的健康状态。

2）采用数据聚类的方法识别监测数据中的模式，通过计算不同时刻数据模式的偏差，来反映系统健康状态的变化，这种通过数据驱动建立的方法，可以避免复杂的机理建模带来的问题，适用于对大规模、复杂程度高的系统进行应用。