火星大气非平衡条件下驻点热流计算公式的探讨

刘方彬，袁军娅

（北京航空航天大学宇航学院，北京100191）

1 引言

火星因为与地球具有很多类似的环境，成为人类空间探索的热点。火星探测器再入时，由于飞行速度很高，再入热环境非常恶劣，因此气动热的计算十分重要，但是其热环境的准确计算目前存在较大的不确定性。然而，对于火星探测器的外形和轨道的快速确定及飞行器的优化设计而言，驻点区域热流的快速准确计算又十分重要。目前可用于火星再入飞行器零攻角驻点热流的计算公式有 Fay-Riddell公式［1］、Sutton-Grave 公式［2］、 Page 公 式［3］、 NASA 经 验 拟 合 公 式［4］、Edquist公式［5］及 Sutton-Grave 修正公式［6］等。 但是，这些公式均未考虑热力学非平衡效应，而火星再入飞行器再入过程中，驻点区域经历明显的热力学非平衡现象［7］，以上公式的适用性和准确性值得探究。

对此，本文先讨论典型的零攻角驻点热流公式——Fay-Riddell公式在计算火星再入飞行器驻点热流的局限性；然后针对Mars Pathfinder（详见文献7）外形和涵盖飞行轨道的大范围计算状态，采用二维轴对称热化学非平衡数值计算方法对完全催化壁条件下的热环境开展数值仿真；利用仿真得到的驻点热流数据进行工程拟合，以得到适用于火星探测器再入飞行过程中连续流阶段热力学非平衡条件下零攻角驻点热流的计算公式，并利用Mars Pathfinder飞行试验数据对公式进行验证。

2 Fay-Riddell公式的局限性

1958 年，Fay等［1］利用多罗德尼津-曼格勒变换和相似性假定，将高温气体边界层偏微分方程转化为常微分方程，和气体热力学特性、输运特性有关的无因此参数假设为一系列常数，Pr＝0.71，Le＝1.0 ～2.0， ρsμs／ρwμw＝ 0.17 ～ 1.0。 利用萨瑟兰黏性定律，在总焓 hs＝（1549 ～24158）kJ／kg，壁面温度Tw＝ （300 ～ 3000）K 范围内，对驻点边界层方程进行了数值计算，得出了式（1）所示完全催化壁条件下的驻点热流估算公式［8］：

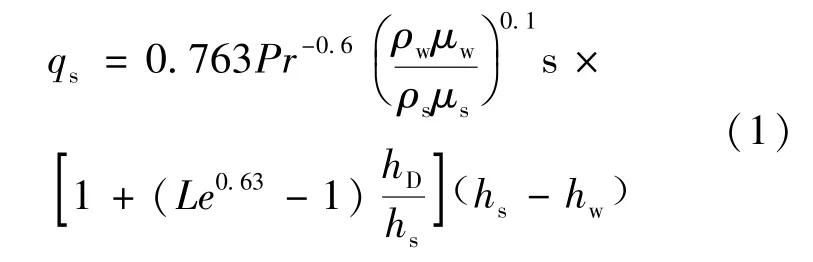
式中：qs为驻点热流；Pr为普朗特常数；Le为路易斯数；ρ为密度，μ为动力粘性，h为焓值；下标“s”和“w”分别代表驻点附近和壁面附近的物理量；hD为空气离解焓；（due／dx）为驻点外缘速度梯度，在高超声速流动情况下，可用式（2）所示修正牛顿流动公式计算［3］：

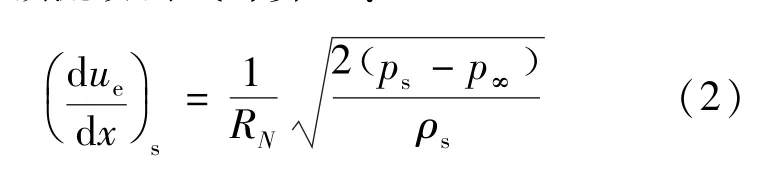
式中：下标“∞ ”代表来流物理量，RN为驻点等效半径；ps为驻点附近压力。Fay-Riddell公式对于火星再入飞行器热力学非平衡计算，有着很大的局限性：

1）Fay-Riddlell公式推导时，对于路易斯数等物理量的选取的时候，采用的是空气的相关参数（详细推导过程见文献［1］），而火星大气的主要成分是CO2，CO2的物理性质和空气的物理性质从粘性、密度等物理量上都有差别［9］。

2）Fay-Riddell公式在理论推导过程中未考虑热力学非平衡的影响，在路易斯数和 ρsμs／ρwμw拟合时采用的数值计算也未考虑到热力学非平衡的影响，仅有化学非平衡的影响。而火星大气环境中，火星大气密度和压力都比地球小两个量级，温度也比地球平均温度低，且CO2本身的气体分子振动特征也比空气低。因此，在火星环境下的高超速流动呈现低雷诺数、高马赫数的特点，热力学非平衡效应明显，在计算中需要考虑到CO2的振动温度［10］。因此，在火星大气条件下，驻点热流计算采用热力学非平衡计算比热化学非平衡计算计算更合适［11］。

采用Fay-Riddell公式对Mars Pathfinder飞行器典型飞行状态［8，11］进行计算，结果如图 1、表 1所示，可以看出，Fay-Riddle公式在高空热力学非平衡效应非常明显的情况下计算误差较大，在56 km时误差为33%，85 km时误差达到40%。

图1 Sutton-Grave公式、Fay-Riddell公式和飞行试验对比Fig.1 Comparison of Sutton-Grave formula fay-Riddell formula and flight experiment

因此，为了更好的估算火星大气条件下再入飞行器的驻点热流，许多研究人员做了不同的假设，采用了不同的方法，其中Sutton等人在1971年根据激波管试验，拟合出了式（3）所示CO2环境下的 Sutton-Grave 公式［2］：

但是Sutton在拟合公式过程中，相应的物理量来源于激波管风洞试验，而风洞条件与真实大气条件下的飞行所得到的参数存在较大差异。采用该公式对飞行条件下驻点热流进行计算，如图1、表2所示，在高空和低空时均存在较大误差，56km时误差为24%，21 km时误差为75%。

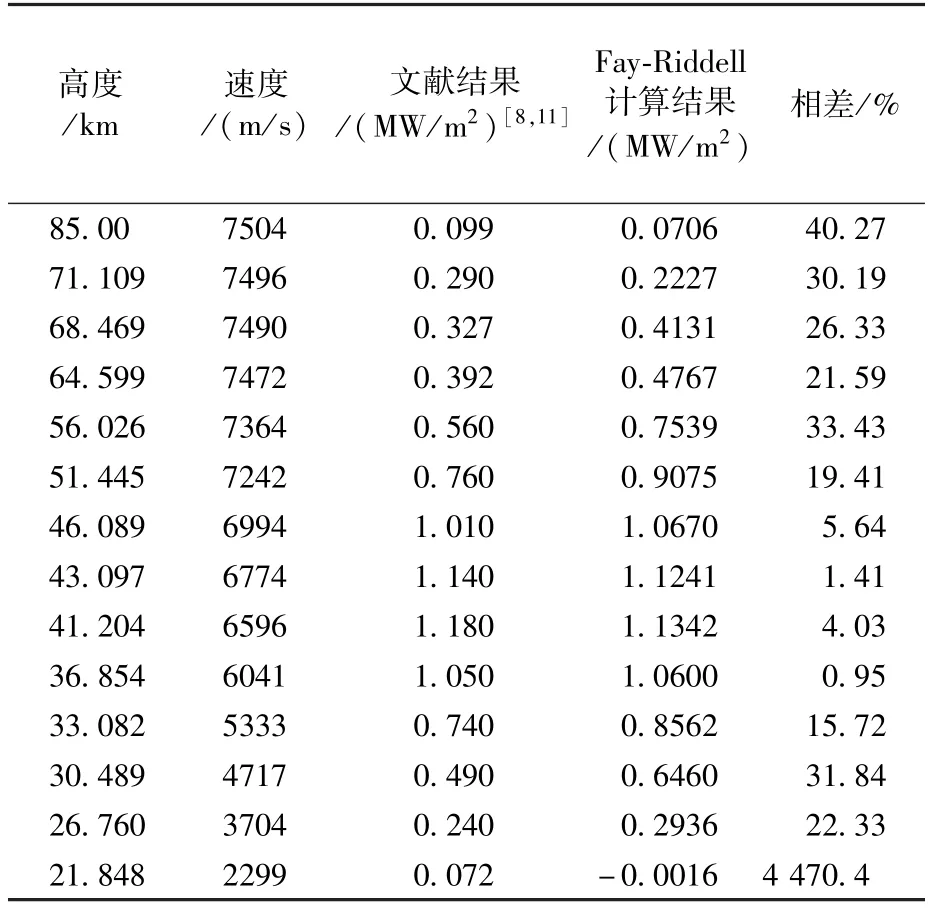
表1 Fay-Riddell公式计算对比结果Table 1 Comparison of Fay-Riddell formula calculation with the results in literature

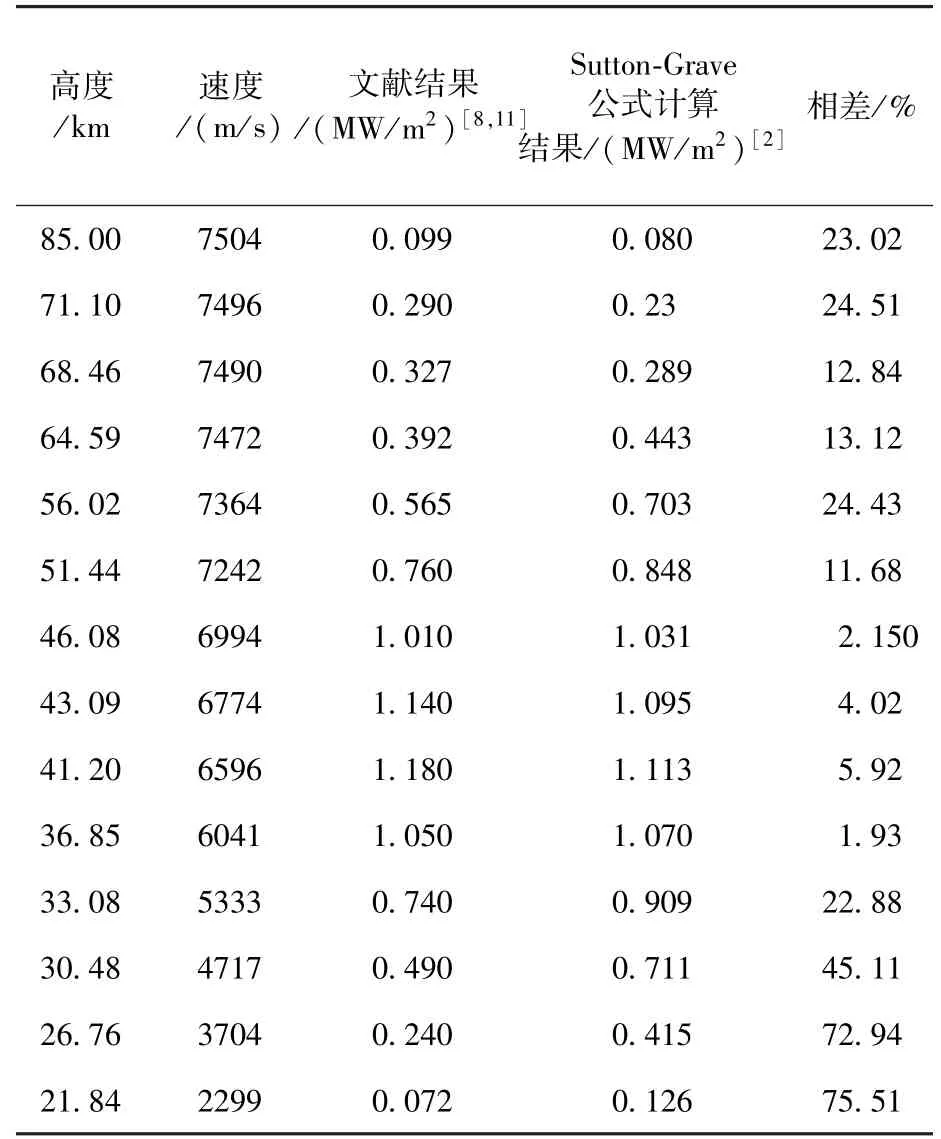
表2 Sutton-Grave公式计算对比结果Table 2 Comparison of Sutton-Grave Formulation calculation with the results in literature

由以上结果可以看出，应对火星大气条件下的再入飞行器的驻点热流公式进行数值仿真和理论分析，以得到适用于飞行条件下的零攻角驻点热流估算公式。

3 数值计算方法

3.1 控制方程和数值方法

考虑零攻角情况，控制方程采用轴对称的化学振动非平衡的流动的无量纲化方程如式（4）：

其中：

这里i＝1，2，…，Ns，Ns为组分个数；t、ρ、p、u、v分别为时间、密度、压力、相对于坐标x和y的速度分量；ρi、fi和Di分别为组分i的密度、质量分数和扩散系数；Ms、hs、evs为组分s的摩尔质量、焓值和振动能（J·mol－1）； E、H0、Ev分别为总能量、焓、和振动能；qv和q分别为振动热流和总热流；Re为雷诺数。部分量有下列关系：H0＝E＋e为总内能；μ∞和μ黏性系数的量纲和无量纲后的值；T和Tv为输运温度和振动温度；ktr和kv为输运和振动的热传导系数。对于化学振动非平衡，状态方程如式（5）：

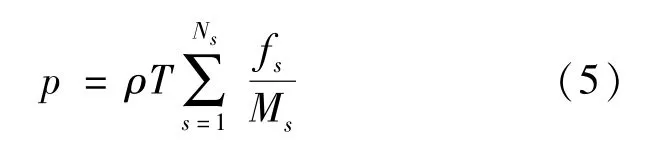
本次数值离散采用简单隐式全耦合TVD格式的计算方法。壁面条件采用满足无滑移条件（u＝v＝0），等温壁条件（T ＝Tv＝Tw），压力法向导数为外边界采用激波捕捉方法，所有变量均为来流值。对称轴满足和v＝0。出口原始变量满足线性关系。以上所有和均采用二阶差分离散。

计算网格采用代数方法生成。为了是网格在物面附近加密以模拟附面层，采用了指数压缩函数来加密网格。

3.2 火星热化学动力学模型

火星大气由97%的CO2和3%的N2组成。化学反应模型考虑v-d耦合效应，假设速率常数为控制温度Tf和Tb的函数，正逆反应速率常数有式（6）～（7）所示关系［2］：

这里 i＝1，2，……，Nr、Nr为反应数；A 为指前因子，B为温度系数，C活化能，f为正向反应，b为逆向反应；Af，i，Bf，i，C，fi见文献［12］，逆反应常数kb，i通过平衡状态获得。本次化学反应为CO2的8组分9化学反应模型，如表3所示，化学反应速率见文献［11］。对于第i个反应对于第i个反应的生成化学源项如式（8）［2］：

第 j种组分的生成化学源项如式（9）［2］：

表3 8组分9化学反应［13］Table 3 Eight Species Nine Reactions Mechanism［13］

对于CO2，由于有三个振动模态，且每个模态对于不同的振动特征温度和特征时间。为了减少控制方程数量，在振动模型中，振动非平衡效应只考虑一个振动温度。则振动能量如式（10）～（11）：

这里θvs是组分s的振动特征问。振动非平衡能量源项Wv为两项之和，一项是输运能与振动能的交换项，另一项是化学反应中分子理解的振动能量的变化项，Wv的计算公式为式（12）［3］：

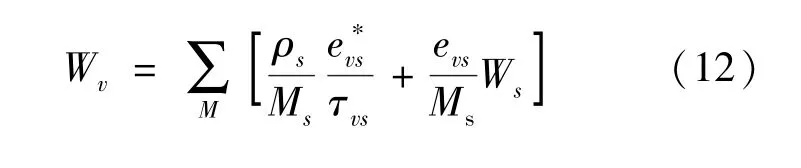
v-d耦合效应在本文中采用简单的Park耦合模型。在该模型中，用控制温度的概念来描述振动非平衡相应对离解的影响，即离解速率用控制温度计算如式（13） ～ （14）：

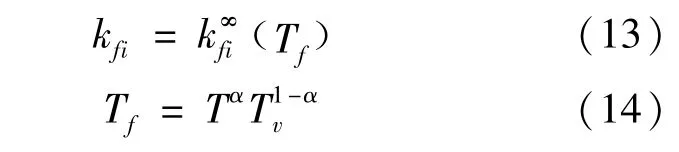
这里的α一般取值范围为0.5≤α≤0.7［3］，本次计算取值为常用的经验值，即0.5。壁面附近化学反应与流场中化学反应相同，其中壁面处考虑完全催化（fi＝0，fi为单原子）。

3.3 数值方法验证

采用Mars Pathfinder的外形进行验证，气体为97%的CO2和3%的N2，验证标准为驻点热流。对于热流数值计算，网格的影响主要体现在法向网格间距上，这里网格无关性分析着重考察法向网格间距的影响。网格如图2所示，计算条件为验证算例工况：Ma＝32，T∞＝ 169 K，Tw＝2000 K，ρ∞＝ 2.8×10－4kg·m3。 计算结果如表 4。

图2 计算网格Fig.2 Computational grid

表4 网格无关性验证Table 4 Validation of grid independence

根据表4可以发现，热流计算对于最小网格间距要求极其严格。因此，在每次更换状态计算时，均需要按照表4方法验证网格无关性，直至计算驻点热流几乎不再变化，以保证计算结果的准确性。

4 驻点热流计算公式拟合

4.1 拟合公式

本章利用数值计算得到的驻点热流数据，重新进行公式拟合，以得到适性更广、准确性更好的驻点热流计算公式。

借鉴 Fay-Riddell公式［1］、Sutton-Grave 公式［7］、Sutton-Gave 修正公式［7］等驻点热流计算公式及其推导过程，可以得出驻点与各个变量之间的关系如式（15）：

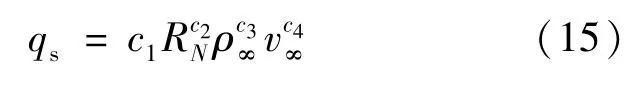
式中： c1，c2，c3为常数。 结合 Sutton-Grave 公式及修正公式，认为Sutton-Gave公式的适用范围较窄的原因在于将壁面温度影响忽略，因此考虑壁面因素的影响，拟采用的公式形式为式（16）：

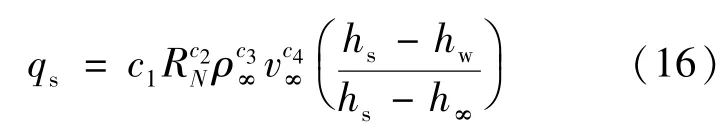
其中hs、hw和h∞分别为驻点焓值、壁面焓值和来流焓值。数值计算的工况以Mars Pathfinder飞行器的轨道数据为基础，如表5所示［14］。

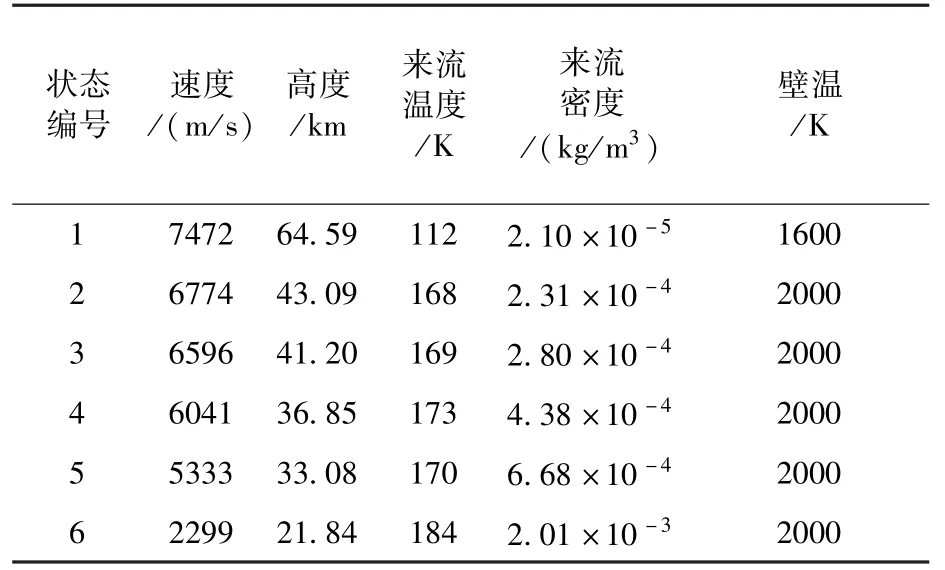
表5 Pathfinder典型飞行参数［14］Table 5 Typical flight data of Mars Pathfinder［14］

4.2 驻点热流与速度的关系

为了建立热流与速度之间的关系，选取的速度的变化范围为 3000 m／s、4000 m／s、5000 m／s、5333 m／s、6000 m／s、6041 m／s、6500 m／s、6596 m／s、7000 m／s、8000 m／s和9000 m／s；其余远场物理量采用表5中状态3和状态4的物理参量。数据拟合时采用线性回归进行拟合，可以得到速度随驻点热流变化曲线如图3。其中纵轴C＝logqs－k为线性回归时拟合到的斜率，来流物理参量为表5状态4时进行的热流计算和拟合。

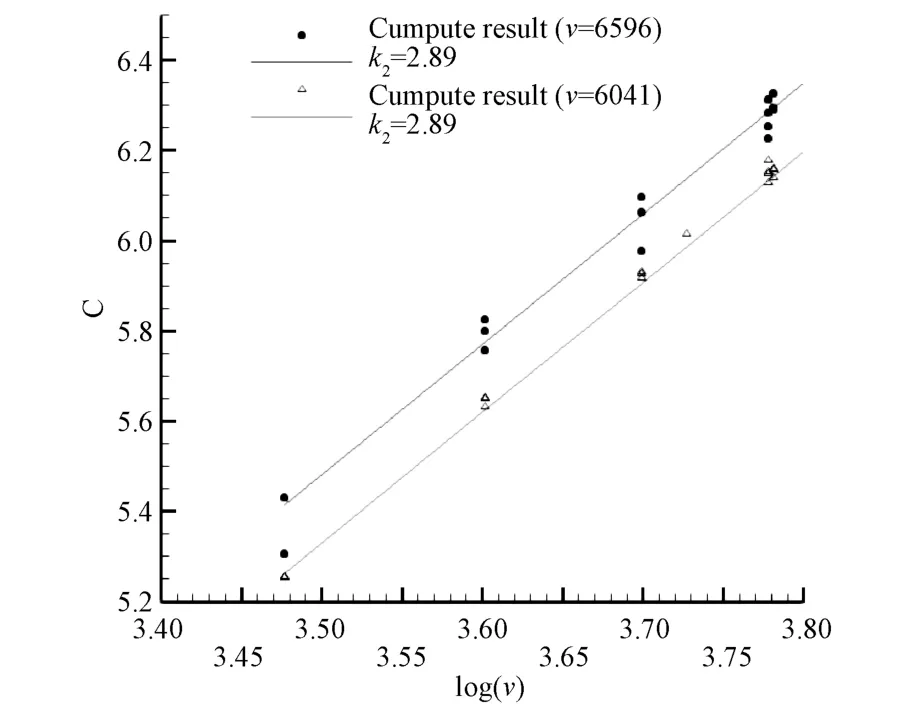
图3 速度-驻点热流变化Fig.3 Relationship between stagnation heat flux＆velocity

根据图3，可以发现驻点热流和速度的2.89次方成线性关系如式（17）：

4.3 驻点热流与半径的关系

为了建立热流与半径之间的变化关系，来流参量采用表5中状态3的物理量。形状为图1中的形状，半径从0.01R到1.4R之间选取95个值，其中R＝0.6638 m。数据拟合时采用线性回归进行拟合，可以得到速度与驻点热流之间的变化关系。其中图 4纵轴 C1＝ logqs－为线性回归时拟合得到的斜率。根据图4，可以得到驻点热流与半径之间的关系如式（18）：

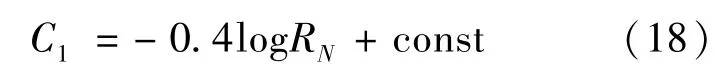
4.4 驻点热流与密度的关系

密度选取表5中的状态3、状态4和状态5的高度进行变化。得到的热流与密度之间的变化关系如图5所示。数据拟合时采用线性回归。其中图5中纵轴为线性回归时拟合到的斜率。

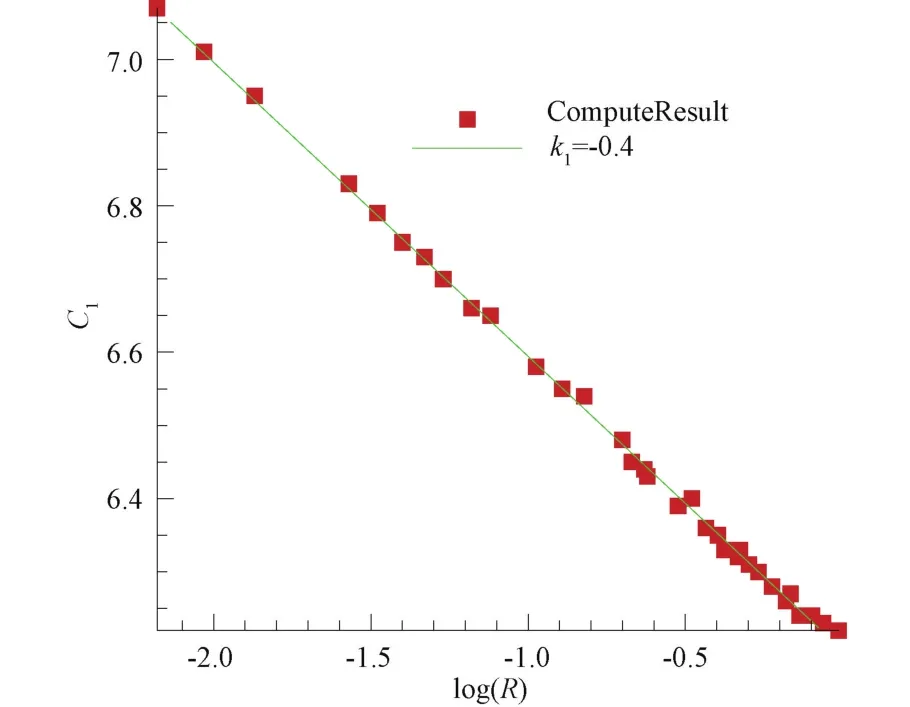
图4 热流-半径变化Fig.4 Relationship between stagnation heat flux＆radius

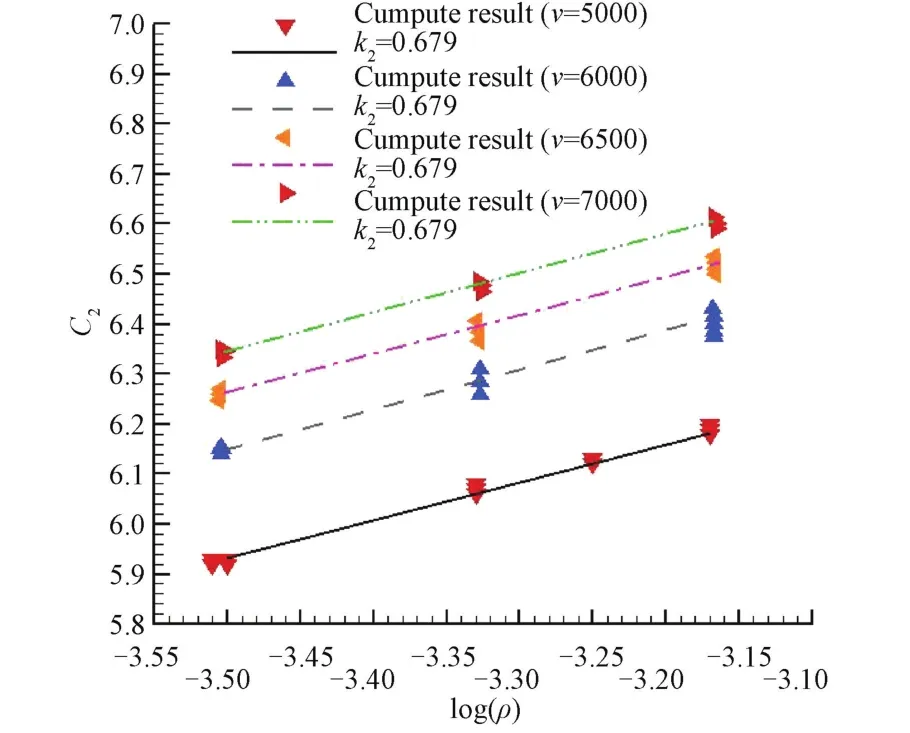
图5 热流-密度关系Fig.5 Relationship between heat flux＆density

根据图5，可以发现驻点热流与密度之间的关系如式（19）所示：

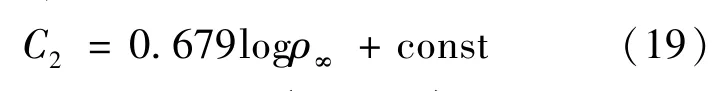
4.5 热力学非平衡下零攻角驻点热流公式

建立热流值与速度、密度和和半径的关系后，进一步采用线性回归进行拟合，如图6所示，可以得到热流的拟合公式。图6中横轴 C3＝纵轴

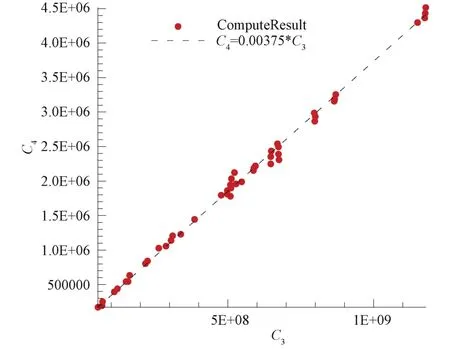
图6 线性关系式Fig.6 Linear formula

根据图6可知，热流密度与来流速度、来流密度和等效半径存在式（20）所示一定关系：

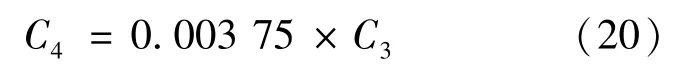
式中：故根据前面计算，得到零攻角驻点热流公式为式（21）：

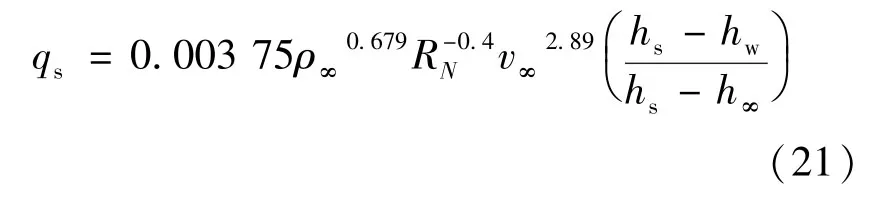
4.6 验证拟合公式的壁温修正

壁温分别取值 1000 K、1500 K、1600 K、2000 K、2100 K、2500 K、3000 K、3500 K、4000 K、4500 K和5000 K，其余参数选取表5中的状态3，验证公式（21）中壁温修正的可行性。得到的热流与密度之间的变化关系如图7所示。图7中qs为驻点热流，单位 MW／m2，横坐标 C5为

进行线性回归求得趋势图，可以得到 qs＝1.8688×C5，而公式（21）在表5中状态3下热流与壁温修正的系数为106＝1.86448，相差2.3%。因此，可以接受公式（21）的壁面修正。

同时也可以发现，壁面温度的取值对于驻点热流的影响也很突出。因此，在驻点热流估算中，也应该考虑到壁面温度对于驻点热流的影响。

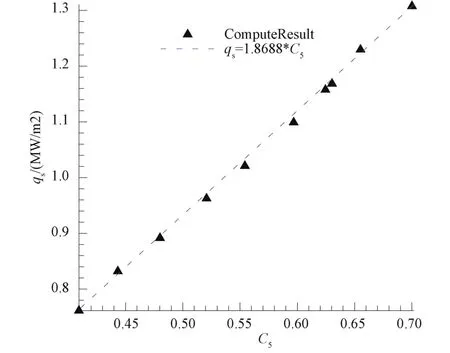
图7 壁面温度修正验证Fig.7 Verification of wall temperature correction

4.7 验证拟合公式

采用拟合得到的计算公式（21）对表1中的工况进行计算，与文献给出的飞行试验数据［14］进行对比，见表6。

表6 拟合公式计算对比结果Table 6 Comparison of fitting formula computation with flight results

从表6可以看出，在双温热力学非平衡高温完全催化壁条件Tw≥1000 K情况下，公式（21）与文献试验数据符合的很好，最大误差为6.25%，可以认为公式（21）能够很好的运用于火星探测器再入过程中的高温完全催化壁面的计算，而且公式（21）的计算高度范围也比Fay-Riddell公式和SuttonGrave公式要宽许多。

5 结论

本文通过数值仿真计算和工程拟合得到的驻点热流公式相对于Fay-Riddell公式，更适合于火星大气条件下的零攻角驻点热流计算：

1）该公式在拟合过程中使用的数据均是在热力学非平衡状态下的数据，比Fay-Riddell公式更适用于火星条件下的热力学非平衡计算过程。

2）该公式采用远场焓作为基准进行壁面修正，比Fay-Riddell的适用高度范围更为宽广。

3）采用Mars Pathfinder的飞行试验数据对比表明，该公式的准确性更高。

4）由于壁面温度对于驻点热流的计算影响很大，因此，需要在驻点热流公式中考虑到壁面温度对于驻点热流的影响。因此，该公式也比Sutton-Grave公式的适用高度范围更宽。

该公式目前仍有不足之处，主要是拟合数据有限，因为目前可查到的有真实飞行试验数据的零攻角再入的火星探测器仅有 Pathfinder。随着后续火星探测器的数据的不断增加，拟合公式还可以进一步验证和细化。