巧设问题串促进学生数学思维发展
□ 文/重庆市江津区四牌坊小学校 金剑 郑华恒
摘要:问题串是训练学生数学思维的“梯子”。巧设问题串,既能使课堂有理有据,逻辑严密,更能促进学生深度反思,提高学生数学思维参与的深度、效度和广度。
关键词:问题串 思维广度 思维深度 思维效度
问题串,即相互联系,逻辑严密的问题系列。问题串能帮助学生步入知识内核,培育学生的问题意识,提高学生思维参与的深度、效度和广度,成为学生思维训练的“梯子”。
本文以几个教学片断为例,探讨教师巧设问题串于学生思维的作用。
一、以“问题”为串,加强思维参与的深度
教师精心预设问题串,引领学生经历有意义的实质性的学习,学生可以在知识的动态形成中,经历思维从外在表面的认识,逐步走向理性的深刻分析。
一个新问题,学生的初始想法往往比较肤浅,思考欠深入,很多时候仅仅是一个大胆的猜测,还需小心地求证。教师适时地以探究性“问题”为串,通过不断的追问、探问,引导学生由表及里,质疑问难。学生在不断地思考、分析中形成递进式思维,对知识经过全面、准确、深刻的理解,真正实现未知变已知,猜测变结论。以片段一为例:
【片段一】
提问1:袋子里共有两个球,任意摸一次,摸到红球的可能性是几分之几?
设计意图:初步感知用分数表示可能性的大小。
提问2:说说你的理由。
设计意图:强化感知,将用分数表示可能性大小的理由抽象出来。
提问3:说得不错,再加一个球,摸到这个球的可能性又是几分之几?
设计意图:引发学生深度思考,发现影响可能性大小的因素。
提问4:为什么?
设计意图:反诘提升,进一步探究影响可能性大小的因素。
设计意图:变化问题,塑造学生思维的可逆性。
设计意图:提升思维难度,将发现的规律总结提升概括出来。
该教学片断中,教师以“说说你的理由。”“为什么?”两次追问确定可能性大小的理由,并通过三个探究性问题为串,三探分母对可能性大小的影响,层层推进,既培养了学生纵向深入思考的习惯和能力,又使学生对教学内容的认识逐渐地清晰明朗;也使教学内容显得有理有据,经得起反思与推敲。
二、以“问题”为串,提高思维参与的效度
“创设问题情境”是数学课堂中常用的一种策略,这可以使原来枯燥、抽象的数学知识变得生动形象、饶有兴趣。难易适度的、有层次的、科学性的“问题”串更能聚焦学生注意力,提高学生思维参与的效度。
设计“问题”串时,应关注教学重难点和学生已有知识经验,考虑好问题的衔接和过渡;把握时机,灵活地、适时地变换问题,引导学生在所创设的问题情境中思考、分析、交流、体悟。以片段二为例:
【片段二】
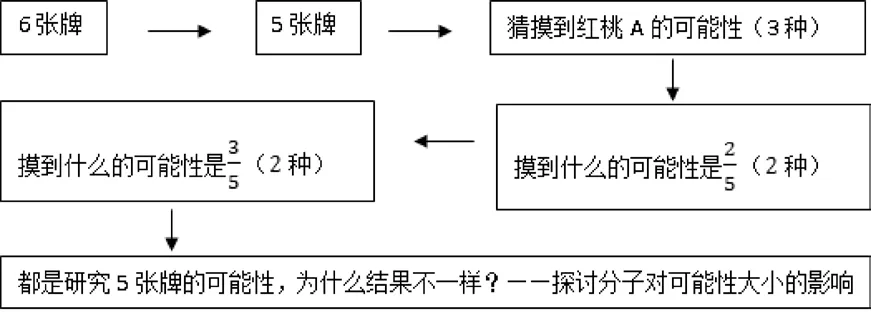
师:我们继续玩牌,(将原来的6张进行变化)这里有五张牌,三张已知(红桃A、2、3),另外两张反扣在桌面上。
师:摸到红桃A的可能性是几分之几?
师:同学们真了不起,(翻开牌面:黑桃4、5)摸到谁的可能性是呢?
生4:黑桃,一共有5张牌,黑桃有两张。
生:因为红桃和单数都有3张,所以摸到红桃或单数的可能性是。
师:都是研究5张牌的可能性,为什么又不一样了呢?
上述教学片断,教师借助“玩牌”创设问题情景,将核心问题进行有目的、多角度、多层次的演变(如下图),促进学生在“新”与“奇”中去理解和掌握此类数学问题的一般规律和本质属性,极大地提升了思维参与的效度。
三、以“问题”为串,拓宽思维的广度
数学是一门严谨的科学,问题串的设计不仅要逻辑严密,还要起到引导学生进行分析、综合、概括、总结、延伸的作用,拓宽学生思维的广度。
“问题串”,应围绕数学知识的有效理解,围绕数学思想方法的有机渗透,尊重学生的已有知识基础,有条不紊,层层铺垫,才能为学生留下可思考、能思考、会思考的空间。否则,“问题”不能为串,“问题引导”将变成机械的“随意问答”,学生思维缺乏连贯性,便无法进行创造与延伸,学生的思维、学习活动也会随着课堂教学的结束戛然而止。那么,如何运用问题串提升学生思维的广度呢?以片段三为例:
【片段三】
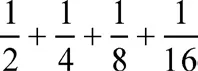
1.常规解法:通分。
2.你能画图来解决这个问题吗?(引导学生分析涂色部分的大小可以用单位“1”减去空白部分的大小,分别是1-,1-,1-1-……)

4.做完这一题,你还能解决像这样的哪些题目,你能试着举出一个例子吗?
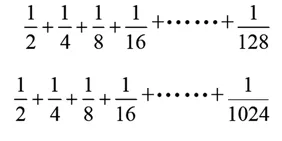
……
学生对一个数学问题的认识,需经过由简单到复杂,由直观到抽象,由表象到本质这样一个循“序”的过程。在该教学片断中,教师将一系列问题为串,帮助学生实现问题的迁移,使学生由此及彼,举一反三,拓宽学生思维的广度.
总之,问题串,是基于解决知识本质,促进学生深度学习的教学策略。作为教师,应把握住核心问题,鼓励学生围绕主题,创造并解决新的问题,引导学生探究知识内核,积淀数学思想方法,提升数学思维品质,发展数学核心素养。◇

