我的数学课程故事
——小课程走进大课堂
□文/重庆市开州区汉丰第一小学 魏大学
由于大班额的困扰,很难让每个孩子都得到充分的展示与发展,我尝试开发“小课程”,即:让孩子们课外收集数学小题,课前轮流上台展讲,然后师生互动交流,及时梳理、整理成册,并有效融入“大课堂”。“大课堂”不仅仅局限于课堂40分钟,更要走出教室、走进生活、融入社会,形成宽广的学习领域。从真正意义上促进以学生为主体的学习模式,促进思想的交融、智慧的碰撞与情感的交流,让学生的思维品质和能力等得到有效的发展。
链接生活 探究真知
记得在三年级时,一个小老师带来了这样一个有趣的问题:同学们用过放大镜吗?有什么感受和发现呢?
一个同学脱口而出:“我爷爷经常用放大镜看报纸!我也用过,那么小的字儿,一下就放大了!”“是的,我也用过放大镜看小蚂蚁,变成大蚂蚁了!那细小的触角就能看得清清楚楚!”……殊不知,大伙儿对这个话题很感兴趣,不由自主地交流起来......
小老师敲敲讲桌,继续追问:“既然大家都知道放大镜,请回答——用放大3倍的放大镜看20度的角,结果是多少度呢?”
全班同学异口同声地回答:“60度”。
小老师笑眯眯地望着我:“有请魏老师点评。”呵呵,好一个小家伙,又把难题抛给我。
由于这个知识点比较生僻,教材上根本就没有正式出现过。仅仅凭借生活中的直接经验,大家都认为是60度。当时,不知咋的,我居然也受到这种氛围的熏陶,被大家的见解所感动。受到这种思维的影响,我一时半会儿也找不到足够的证据来推翻,似乎“少数服从多数”默认了……大伙儿对于这个答案好像也挺满意。
开课了,大家似乎忘记了这个,看似简单却又不一般的小题。而我,却一直在思索着、考究着……突然,直角三角板闪现脑海——灵感来了!如果用这个放大镜去观察直角呢?这不是一个很好的例子吗?我暗暗惊喜,心里就这样盘算着……
快要下课了,我找准了时机,话锋一转:“课前小老师出的问题,用放大3倍的放大镜看20度的角,大家都认为是60度,但是我还有疑问!”话音刚落,教室里一阵骚动,大伙儿都露出惊讶的神情,简直不敢相信“老师居然也反悔了”。
我镇定地说:“请大家想一想,如果用这个放大镜去观察一个直角呢?猜一猜:你看到的会是什么结果呢?请回家做一做实验,明天小组分享,好吗?”
第二天,大伙儿带着放大镜和三角板,争先恐后地上台汇报:“90度!”“90度!”“用放大镜观察直角,面积变大了”“形状没有变化”“角度也没有变化,直角还是直角”“……”
听着大家的汇报,我露出了欣慰的笑脸,不时点头表示同意……我趁热打铁马上追问道:“昨天小老师出的问题,用放大3倍的放大镜看20度的角,大家还认为是60度吗?”
大家齐刷刷地提高了嗓门,自信地回答:“不是60度,应该是20度!”教室里响起了和谐自信的掌声……学生们又一次明白:学习的有趣来自于链接生活,学习的争论来自于大胆猜测,学习的真知来自于操作探究。
当然,类似链接生活的课程小故事还有很多,比如:到超市去发现体验购物中的数学问题、在生活中从不同角度去观察物体等等。正因为我不是把知识直接硬灌给学生,而是巧妙安排,孩子们留下自主探索、独立思考的空间,让他们回归于生活,自己动手实践,在操作中观察,在验证中感悟,在探究中寻得真知,在交流中获得发展。
打破常规 拓展应用
那是在学习圆面积之后,小老师抛出了这样一个问题:怎样求圆的面积?
有的同学说:可以已知圆的半径求出圆的面积,采用公式S=πr2计算;
有的同学说:可以已知圆的直径求出圆的面积,采用公式S=π()2计算;
有的同学说:还可以已知圆的周长求出圆的面积,采用公式S=π()2计算。
小老师评价追问:看来,大家掌握得非常好。求圆的面积一般先要知道什么已知条件?
同学们回答:要知道圆的半径!!
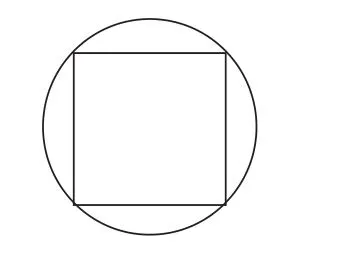
小老师说:是的,这是通常采用的方法。下面这个题就是在圆中
画了一个最大的正方形,就请大家来尝试一下吧。
如图所示: 已知S正方形=36平方米,求出S圆。
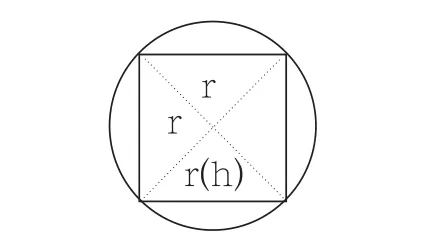
此题中正方形和圆有什么联系呢?怎样求出圆的半径呢?很多同学用以前的老办法固然行不通,有的咬着笔杆冥思苦想,有的低声讨论,也有个别数学小博士露出笑脸……我看在眼里,喜在心里。
终于,开始汇报展示了,如图所示:
画出正方形的两条对角辅助线,也就是正方形
的两条对称轴所在的位置(肯定互相垂直于圆心),那么一条对角线即是该圆的直径(d=r+r),对角线的一半即是该圆的半径(r)。不难看出:
一条对角线将正方形平分为两个等腰直角三角形。
圆的直径(2 r)相当于这个三角形的底(a);
圆的半径(r)相当于这个三角形的高(h)。
则S三角形=(2r)×r÷2=2r2÷2=r2,
所以有S三角形×2=S正方形成立,即:r2×2=36,可以求出r2=18(平方米)。
那么,该圆的面积就能求出来了:S=πr2=3.14×18=56.52(平方米)
此时,教室里一片惊叹与轰动……哇!不求出半径,同样可以求出圆的面积!
在此题的启发下,在后面的展讲中,接二连三地呈现了很多拓展小题。
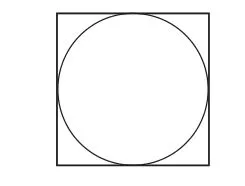
比如:在一个正方形中画一个最大的圆,
如图所示:已知S正方形=40平方厘米,求S圆。
因为正方形的边长和圆的直径相等,即正方形的边长a等于圆的直径d(2 r),因为S正方形=a2=40平方厘米,即S正方形=2r×2r=4r2=40平方厘米,所以,r2=10平方厘米。则该圆的面积是:S=r2=3.14×10=31.4(平方厘米)
在这样的比较特殊的拓展训练中,只要我们善于引导,定会发现有很多数学习题蕴藏着许多巧妙有趣的解法。让学生体验学习和创造的过程,培养学生正确的数学观,引领孩子在巧妙而多彩的数学生活中享受到快乐,思维得到训练与发展。
小课程虽然短小,但它意义非凡,具有积少成多、聚沙成塔的作用。通过尝试,我们班的孩子个个能展示、人人会创新。我相信,在我的坚守研究中,“小课程走进大课堂”会成就更多的大智慧!◇

