常规型抽油机动态仿真与关键部件有限元分析

徐光亿，张 力，贾存千，张立华，韩文洁

(兰州理工大学机电工程学院，甘肃 兰州 730050)

目前油田所用采油设备以自主研制的常规型游梁式抽油机为主[1-2]。近几十年来，随着我国石油钻采行业的快速发展，各油田采油工况日趋复杂化，井深增加，抽油机的负载增大，抽油机的故障率日趋上升。常规型抽油机的运动速度、加速度峰值、扭矩因数峰值、曲柄轴净扭矩峰值都较大，存在负扭矩、能耗大等缺点[3-4]。因此，研究常规型抽油机的运动形式、动态特性以及重要部件的应力应变情况，并以此作为抽油机优化的依据具有一定的现实意义。

1 抽油机运动学分析

为了研究抽油机各个部位的力学特性，分析各部件受载情况，就必须清楚抽油机整机的运动规律。这不仅是后续计算、分析的前提条件，更是抽油机整机动态仿真分析的基础。常规型抽油机机构简图如图1所示。

图中符号说明：A为中心支撑至光杆中心线的距离，即游梁前臂长，mm；C为尾部支撑至中心支撑的距离，即游梁后臂长，mm；P为连杆长，mm；R为曲柄半径，mm；K为中心支撑至曲柄回转中心的距离，即基杆长度，mm；H为中心支撑至底座上平面的高度，mm；G为曲柄回转中心至底座上平面的距离，mm；I为曲柄回转中心至游梁支撑中心线的距离，mm；J为曲柄轴中心线至游梁支撑中心线的距离，mm；θ为曲柄转角，从井口向右侧观察，曲柄

图1 常规型抽油机机构运动简图

顺时针方向旋转时偏离其竖直向上位置的转角，rad；α为连杆与曲柄之间的夹角，rad；β为连杆与尾部支撑和中心支撑连线的夹角，即传动角，rad；χ为尾部支撑和中心支撑连线与曲柄轴中心线和游梁支撑中心线连线的夹角，rad；ψ为尾部支撑和中心支撑连线与中心支撑和曲柄回转中心连线的夹角，rad；ρ为中心支撑和曲柄回转中心连线与曲柄轴中心线和游梁支撑中心线连线的夹角，rad；θK为中心支撑和曲柄回转中心连线与曲柄之间的夹角，由中心支撑和曲柄回转中心连线到曲柄沿曲柄旋转方向度量，rad；φ为中心支撑和曲柄回转中心连线与零度线的夹角，由中心支撑和曲柄回转中心连线到曲柄沿曲柄旋转的方向度量，rad。

由图1可知：

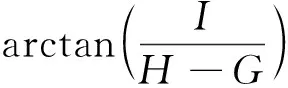
(1)

θK=θ-φ

(2)

式(1)中，正号表示曲柄顺时针旋转，负号表示曲柄逆时针旋转。

由图1几何关系得：

J2=K2+R2-2KRcosθK

(3)

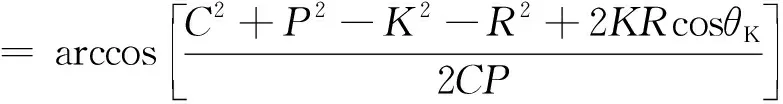
(4)

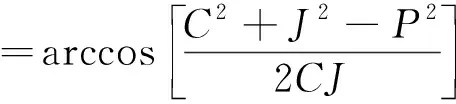
(5)

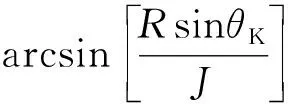
(6)

式(6)中，正号表示曲柄顺时针旋转，负号表示曲柄逆时针旋转。

另外，关于几何结构计算中涉及的间接变化量有如下关系：

(7)

式中：θ0为悬点位于下死点极限位置时连杆与零度线位置的夹角,rad。

(8)

式中：θ1为悬点位于上死点极限位置时连杆与零度线位置的夹角,rad。

θ2=2π-φ+θ

(9)

式中：θ2为曲柄逆时针旋转时与OO′的夹角,rad。

(10)

式中：θ3为连杆与OO′的夹角，rad，逆时针为正。

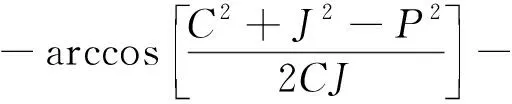
(11)

式中：θ4为OO′与游梁的夹角，rad，逆时针为正。

由图1知，连杆和游梁的角位移分别是：

θG=φ-θ3

(12)

θL=π+φ-θ4

(13)

式中：θG为连杆与零度线的夹角；θL为游梁前臂与零度线位置的夹角。

另外，抽油机机构参数还存在以下关系：

R+P=K+C

(14)

式(14)用复变矢量表示如下：

Reiθ2+Peiθ3=K+Ceiθ4

(15)

式中i为一个虚数单位。

将式(15)两边求导得到：

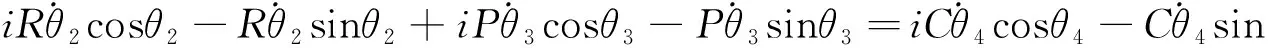
(16)

并且得到：

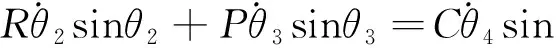
(17)

(18)

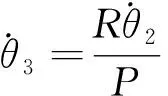
(19)

(20)

(21)

(22)

式中：ω为曲柄角速度，rad/s。

(23)

式中：n为曲柄的转速，r/min。

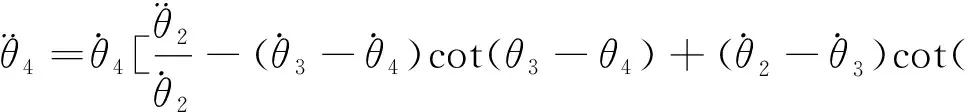
(24)

εL=-ωL[(ω-ωG)cot(θ2-θ3)+(ωG-ωL)cot(θ3-θ4)]

(25)

将上述计算结果代入式(25)，得到游梁的角加速度为：

(26)

2 抽油机的动态仿真

2.1 抽油机虚拟样机的建立

建立抽油机的虚拟样机模型通常有两种方法。第一种是用ADAMS软件自带的建模功能建模，可以自动生成质心坐标、实体质量和质心相对回转半径等参数，这些数据可直接用于分析中。此种建模方法简单，工作量小。第二种是运用其他三维软件进行建模，然后经格式转化后导入ADAMS软件中，再对各个部件添加材料属性和质量等。这种建模方法的优点是建立的实体模型比较精确，能够获得理想的仿真效果[7-8]，因此本文采用第二种方法。

本文以C-456D-305-144抽油机为例，首先在UG软件中画出抽油机的各个部件，然后将各个部件装配完成后转化为Parasolid格式文件，并将其导入ADAMS软件中，经过适当的编辑转变为ADAMS中的刚体。其模型如图2所示。

图2 抽油机的虚拟样机模型

ADAMS仿真分析前需要确定各个构件的运动关系，这就要求根据抽油机的运动情况对所建立的物理模型添加相对应的约束关系，主要包括固定副、旋转副等等，其约束见表1。

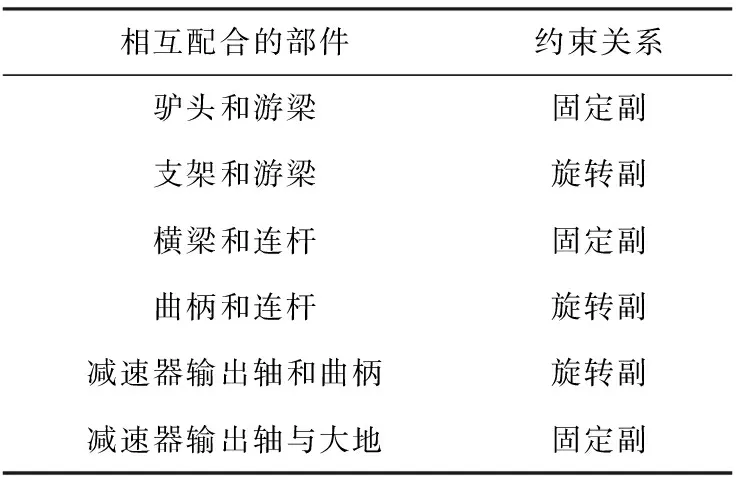
表1 各个部件的约束关系

2.3 施加载荷

C-456D-305-144抽油机冲次为16spm，经过换算得到曲柄转速为96(°)/s，则运动函数表达式为96d/s。载荷施加采用光杆最大载荷138 000N，施加在驴头悬点上面。设置相应的仿真时间和仿真步数，开始仿真分析。

2.4 运动学仿真

运动学仿真的目的是研究抽油机系统构件的位置、速度和加速度的变化规律。图3～图5分别是抽油机驴头悬点的位移、速度、加速度的仿真曲线图。

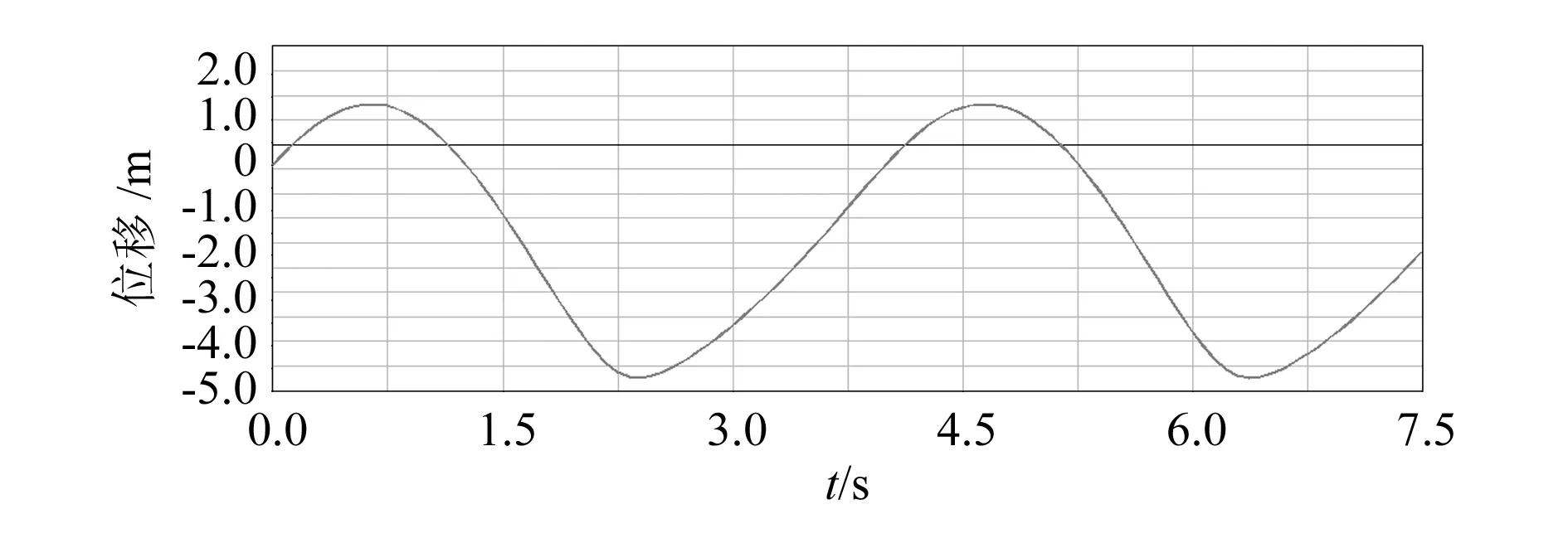
图3 悬点位移仿真曲线图

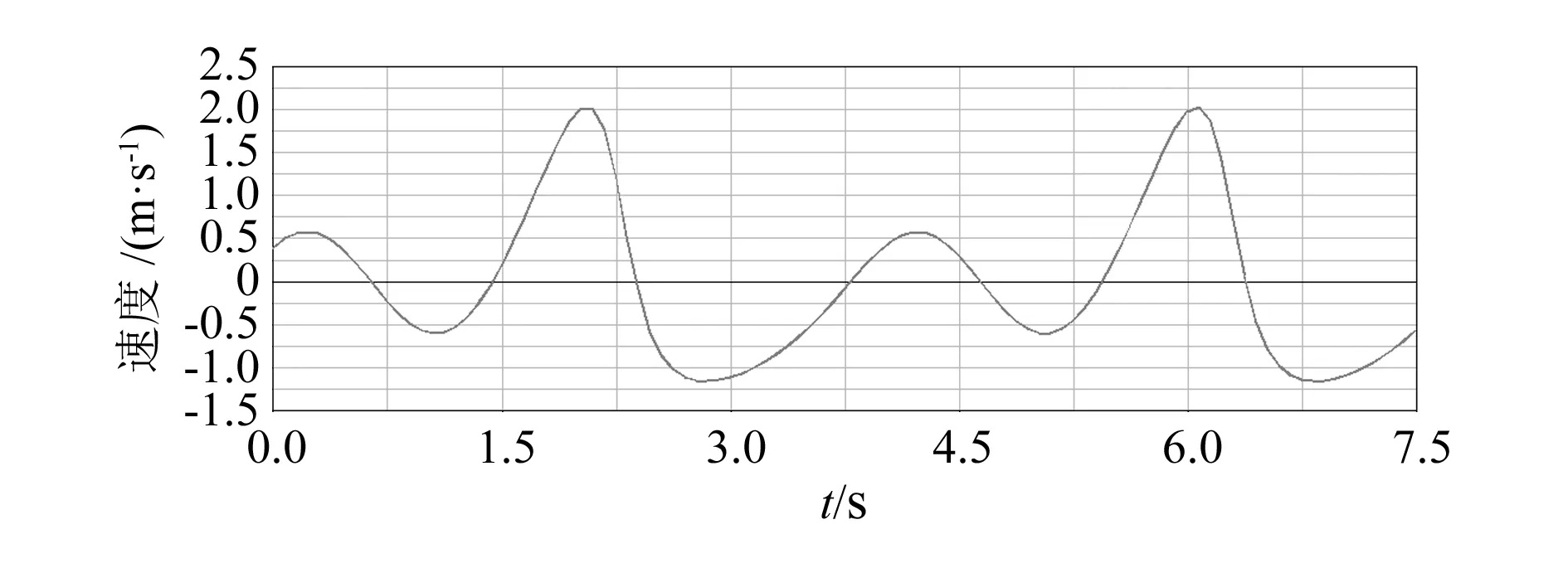
图4 悬点速度仿真曲线图

图5 悬点加速度仿真曲线图

从图中可以看出，悬点位移曲线和速度曲线呈接近正弦变化规律，悬点加速度曲线在上下死点位置时的波动比较大。

2.5 动力学仿真分析

动力学分析就是研究抽油机在载荷作用下的动力学响应。图6和图7分别是抽油机中心支撑处的受力和横梁支撑处的受力随着时间变化的曲线图。

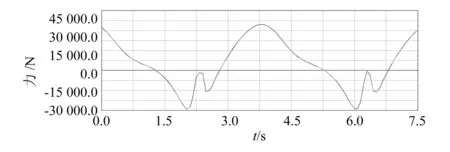
图6 中心支撑处的受力曲线

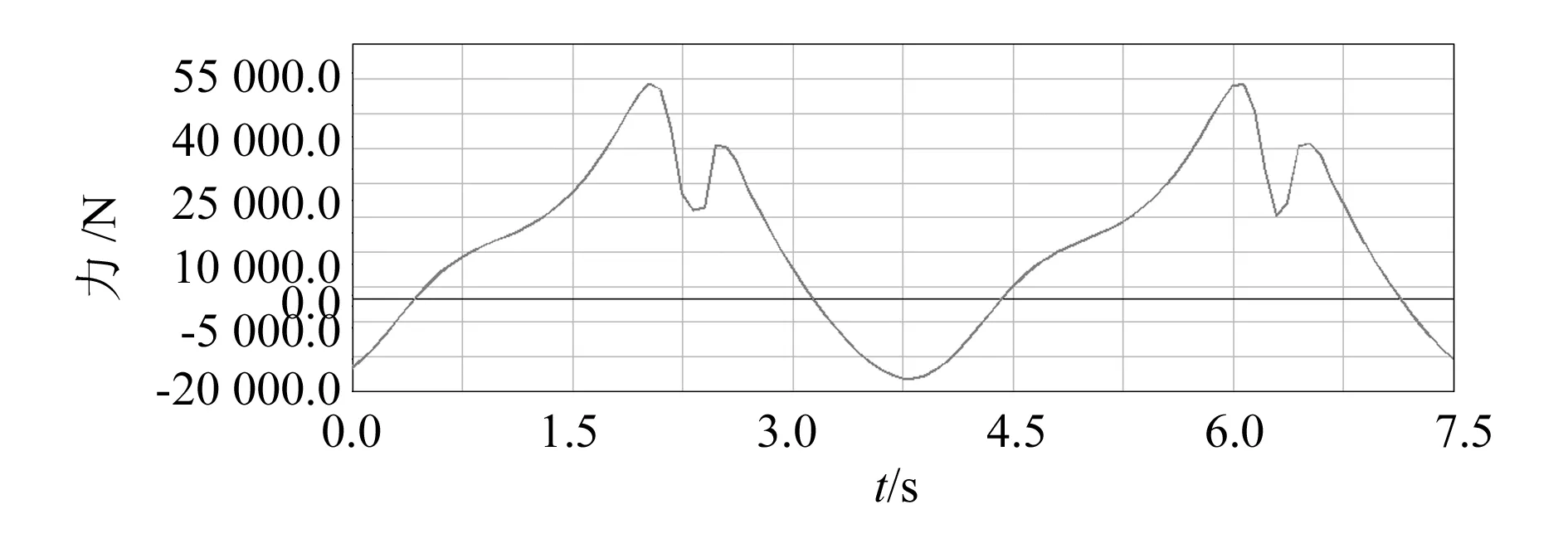
图7 横梁支撑处的受力曲线

3 关键件的有限元分析

3.1 游梁的分析

游梁材料选用Q345-B。ANSYS分析结果如图8～图10所示，分别为游梁的总变形云图和应力、应变云图。

图8 游梁总变形云图

图9 游梁应变云图

图10 游梁应力云图

由图可以看出，游梁的最大变形发生在尾轴承边缘处，最大变形量为6.432 33mm；最小变形发生在中心支撑处；在中心支撑处出现应力集中，应力最大。

3.2 连杆的分析

连杆上下接头材料选用Q235，钢管材料选用20#无缝钢管。图11～图13为连杆的总变形云图和应力、应变云图。

从图中可以看出，连杆最大变形小于0.958 49mm，其变形量很小；连杆受力最大时，连杆整体应变处于0.450E-08与0.949E-04之间；连杆受力最大时，较大的应力集中发生在中间管端部的凹槽与连杆接头的连接处。连杆与接头的焊缝处容易出现应力集中现象。

图11 连杆总变形云图

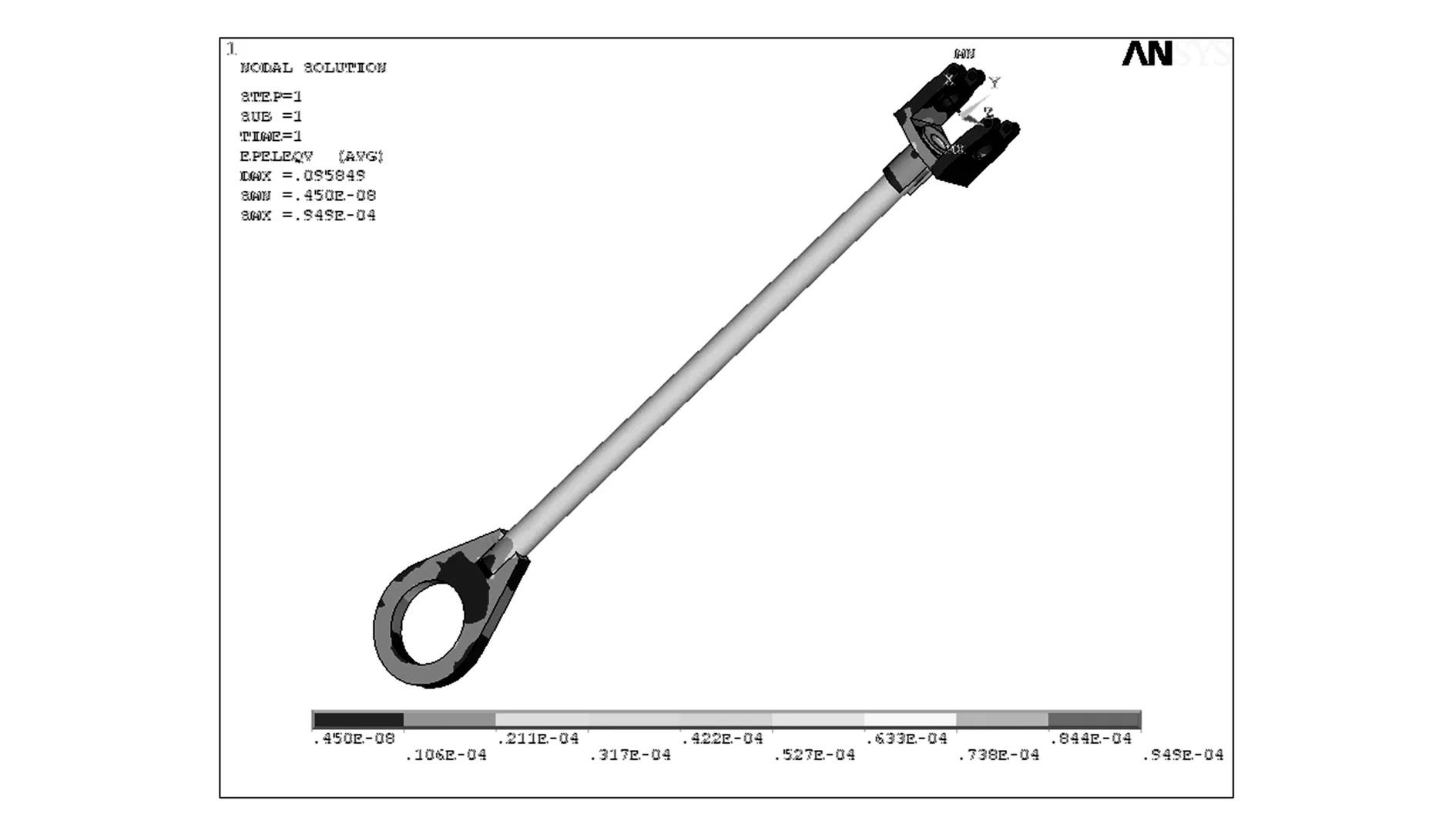
图12 连杆应变云图

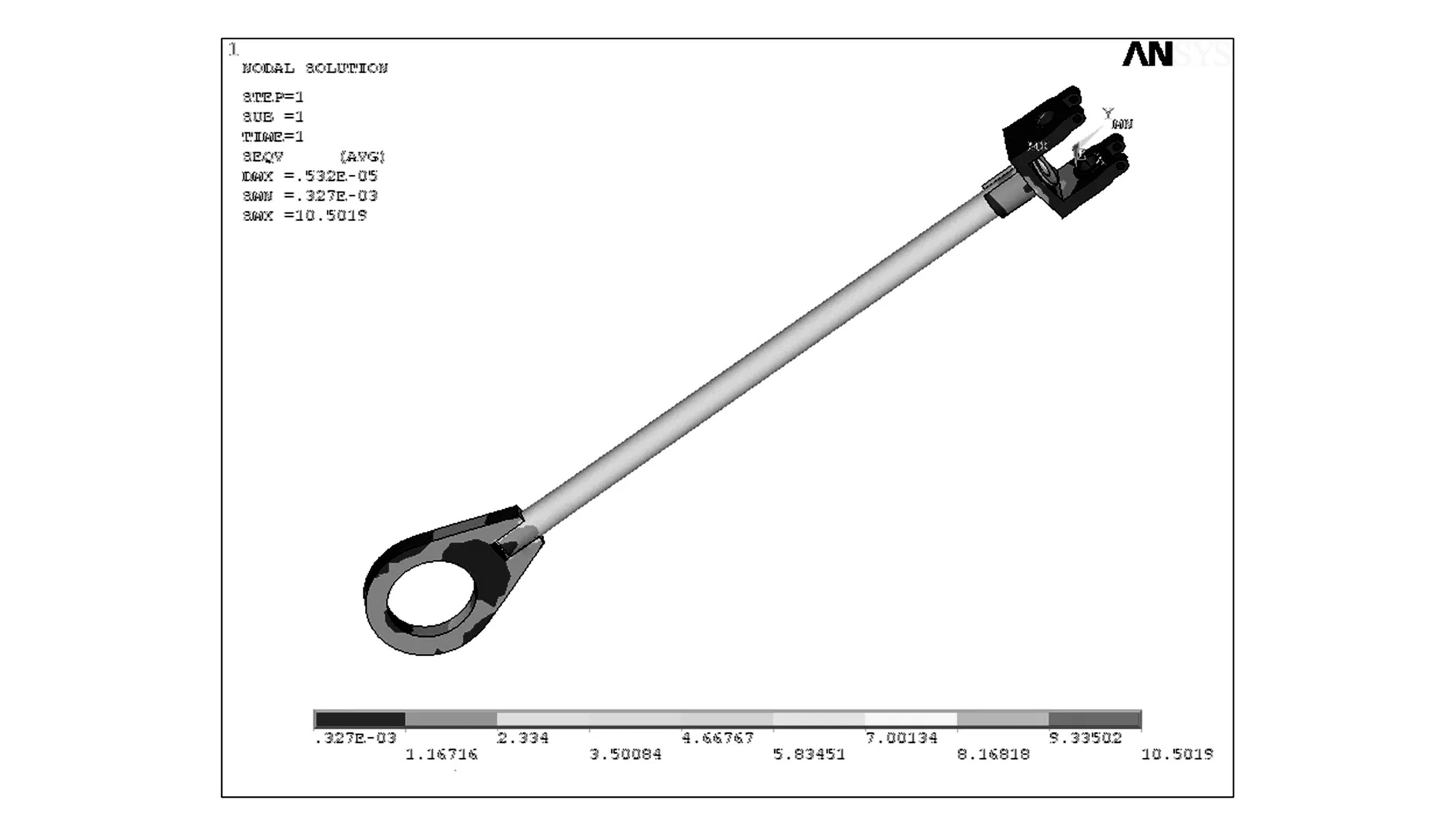
图13 连杆应力云图

4 结束语

本文运用虚拟样机技术与有限元分析相结合的方法，得到了抽油机悬点的运动规律、各构件受力情况的仿真曲线图和游梁、连杆的应力应变云图，分析了仿真曲线并得到了游梁、连杆的变形量和应力集中位置等，为C-456D-305-144抽油机的优化设计打下了一定的基础，也为常规型抽油机的改进和设计提供了理论研究与分析方法。