齿轮抗磨性能参数建模分析与仿真

朱国勇

(南宁职业技术学院机电工程学院，广西 南宁 530008)

在现代机械化生产中，齿轮发挥了非常重要的作用，但在机械运行过程中，齿轮的磨损消耗相当严重。其中最常见的齿面磨粒磨损是由于啮合齿面间的相对滑动，使一些较硬的磨粒进入摩擦表面，从而使齿廓改变、侧隙加大[1]。一般情况下，只有在润滑油中夹杂磨粒时，才会在运行中引起齿面磨粒磨损。齿轮磨损故障导致机械化设备难以良好运行，降低了机械生产的质量和数量。因此在齿轮平面设计和质量检验中，对齿轮的抗磨性能进行分析至关重要。齿轮的抗磨性能分析过程也就是齿轮磨损量的计算过程，齿轮的磨损量计算值越小，表明其抗磨性能越好，反之越差[2]。

文献[3]根据Hertz理论和Archard磨损公式，建立面向真实工况的齿轮磨损有限元模型，并对其齿面磨损特性进行了数值仿真，但该方法存在参数准确性不足的问题，容易使测量结果不准确。文献[4]通过分析渐开线圆柱齿轮的参数化建模关键技术，构建渐开线圆柱齿轮模型，但该方法存在参数计算准确性较低的问题。针对上述存在的不足，本文通过建立新型齿轮磨损量计算模型，对齿轮抗磨性能参数进行分析。

1 齿轮磨损程度参数选取与计算

齿轮的磨损过程可以看作是一个随机离散化过程，齿轮抗磨性可通过磨损量参数计算结果来体现，齿轮磨损受力角度计算简图如图1所示。

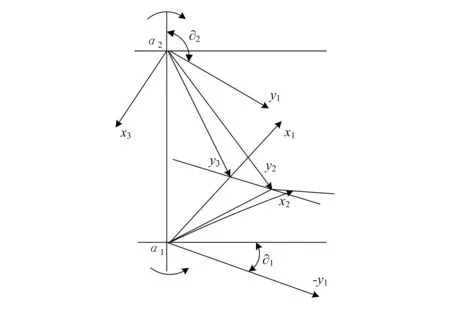
图1 齿轮磨损受力角度计算简图

1.1 齿轮参数选取

齿轮的样式较丰富，不同的齿轮抗磨性能不同，其磨损程度也就不同，这就导致分析起来相当困难。因此本文对该齿轮的12种参数：齿数、模数(mm)、齿顶高系数、顶隙系数、变位系数、齿宽(mm)、中心距(mm)、啮合角(°)、传递功率(kW)、制作材料、强度(HB)和热处理进行加权处理，最后将综合加权参数作为磨损性能分析的对象。

1.2 受力扭矩的计算

由于相关参数是以应力的形式被量化的，应选用合理的实验载荷。本文选取接触应力并对其进行计算，简言之，施加在齿轮上的载荷应无限接近许用应力。

许用接触应力σHP的数学表达式为：

(1)

计算接触应力σH为：

(2)

式中：ZN为载荷分布的最大值；ZL为载荷分布的最小值；F为齿轮的圆周力；SH为屈服极限；u为齿轮受力常用值。

设许用接触应力σHP=X，其中X为未知数，单位为N/mm2。用σHP的值代表计算应力，得到该齿轮的圆周力F=μX，单位为N，其中μ为应力系数。这时应施加在齿轮上的扭矩T为：

(3)

根据扭矩T的计算结果，选用三级载荷作为实验齿轮所要承载的压力。

1.3 分析模型的设计

实验齿轮在载荷的作用下，随着时间的推移，该齿轮的厚度开始磨损变薄。当达到一定程度后，轮齿间的间隙会越来越大，最后极有可能发生轮齿断裂现象，导致该齿轮的功能丧失，影响机械的正常运转[5]。因此在对齿轮磨损程度的分析中，把齿轮厚度作为约束指标，结合12个参数分析齿轮的抗磨性能。

在齿轮的平面设计中，当确定了齿轮的制作材料后，安全系数和载荷等级就成为齿厚参数选取的决定性因素，而安全系数与载荷等级产生的弯曲应力以及齿轮制作材料的弯曲疲劳极限密切相关[6]，关系可用式(4)表示：

(4)

式中：R为安全系数；D1为齿轮的弯曲疲劳极限；D2为弯曲应力；D3为弯曲应力修正系数；D4为齿轮的寿命系数；D5为齿轮尺寸系数。

为方便计算，可以把式(4)转化为：

R=σHPF-1Dnn=1,2,3,4,5

(5)

除了齿轮的制作材料外，齿轮的承载力也是决定齿轮各参数设置的主要因素，因此当齿轮承受三级载荷时，其初始抗载荷系数H1为[7]：

(6)

式中：M为载荷作用下齿轮承受的弯矩。

材料强度决定的齿轮抗弯系数H2为[8]：

(7)

式中：σHP′为许用挤压应力。由于在齿轮的平面设计中，齿轮的宽度是明确的，根据式(5)、(6)、(7)可以将式(4)改写为：

(8)

式中：S1为由载荷决定的齿轮厚度；S2为由制作材料决定的齿轮厚度。

为了保证机械安全运行，机械中的齿轮安全系数必须大于等于1[9]，因此通过式(8)确定其约束条件为：

S1≥S2

(9)

令

S2=S1-ΔS=S-ΔS

(10)

则磨损后的剩余齿厚为：

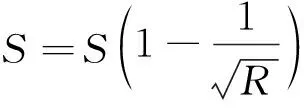
(11)

式中：S为现齿厚；ΔS为磨损后的剩余齿厚，由它可算得齿轮的最大磨损量=齿原始厚度-现齿厚。ΔS值越小，则磨掉的部分越多，也就是磨损程度越高、抗磨性能越差；ΔS值越大，则表明磨损程度越低、抗磨性能越好[10]。

2 案例分析

为验证上述齿轮磨损量计算模型的有效性，对其进行实际案例分析。

以某食品加工厂的生产机械为例，其机械设备中的齿轮已经运行了3a，再加上长时间处在低温、潮湿的环境中，齿轮表面已经出现大面积磨损，并有大量的碎屑堆积，磨损情况严重，具体情况如图2所示。

图2 齿轮磨损图

为验证图2中齿轮的抗磨性能，需要对其进行磨损量计算。首先利用齿厚测量仪对图中的齿轮厚度进行测量[7]。测量得该齿轮的厚度为4mm，较之前减少了2mm，即磨损了2mm，如图3所示。

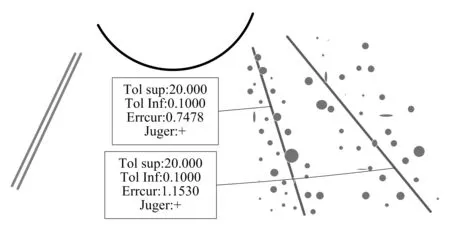
图3 齿面磨损量检测数据拟合图

对比表1的磨损程度标准，可知图中齿轮的磨损程度为严重磨损，即该齿轮的抗磨性能差。

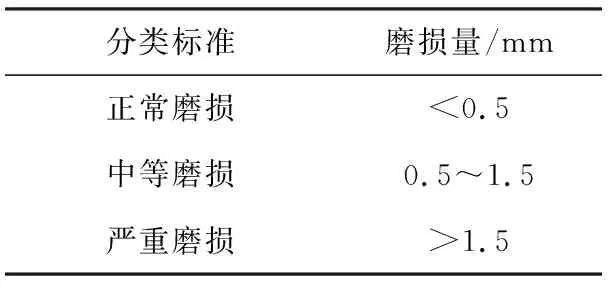
表1 磨损程度标准

利用本文建立的齿轮磨损量计算模型对图2中的齿轮进行磨损量计算。模型所需要的齿轮各参数值见表2。

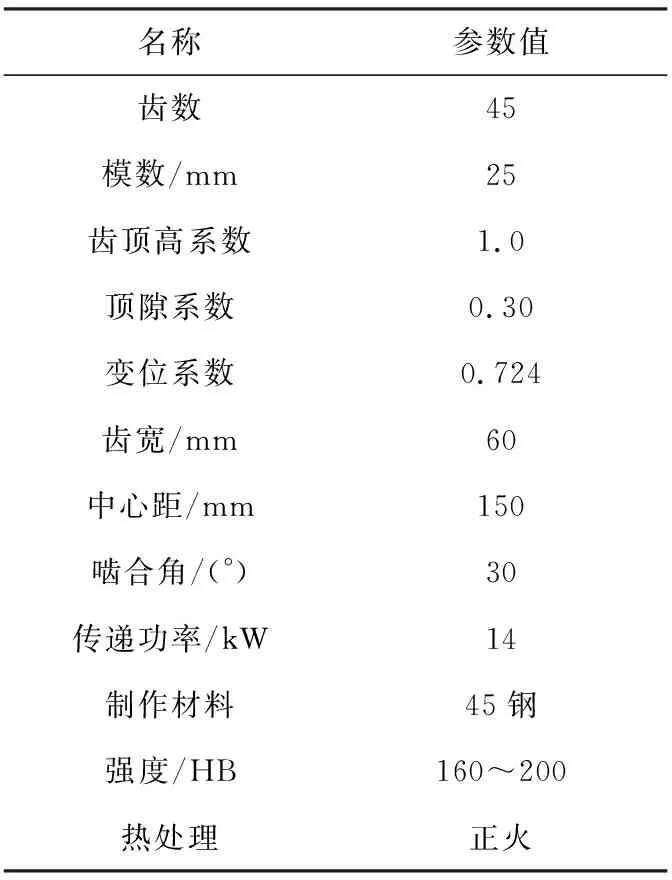
表2 图2中齿轮的参数

把表2中的相关参数值代入式(8)～式(11)中，计算得ΔS=2mm。

上述计算结果与通过齿厚测量仪测试的结果一致，证明了本模型的有效性。

为进一步验证利用该模型进行抗磨性能分析的准确性，现分别利用本文建立的新型模型和有限元模型对图2中的齿轮磨损量进行计算，为保证实验的客观性，分别利用两种模型进行了10组对照实验，对比结果如图4所示。

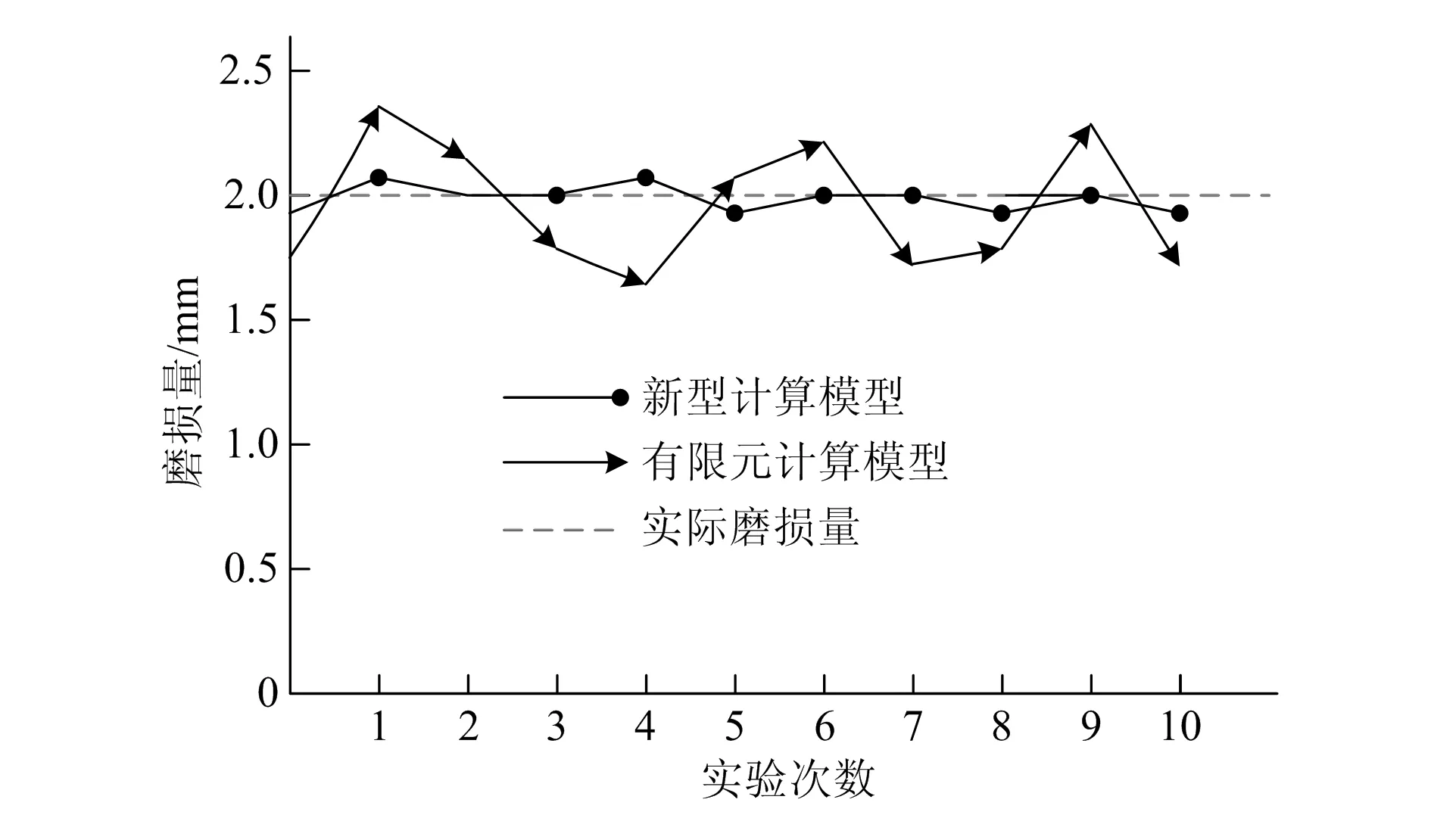
图4 两种模型计算准确性对比图

从图4中可知，本文建立的新型模型计算结果非常接近实际磨损值，平均误差为1.0mm，而有限元模型计算出来的结果与真实结果存在一定的差距，平均误差为2.5mm。这两种模型计算出来的平均误差相差1.5mm，新型模型的准确率比有限元模型提高了25%。由此可知新型模型抗磨性能分析准确性要高于有限元模型。此外，从图中两条曲线的走势上看，新型模型波动较小，计算结果一致性和稳定性好；而有限元分析模型波动较大，一致性和稳定性差。

3 结束语

本文建立的齿轮磨损量计算模型通用性较强，为实现齿轮抗磨性能分析、保证机械正常运行提供了一种新的方法。但因齿轮型号多样，每一种型号的齿轮都具有不同的特征，而本文方法并未考虑所有型号齿轮的特征，因此研究结果存在一定的局限性，还需要后续进一步分析和改进。