矢量过偏心孔中心的多个外周孔加工

田立波，王文静

(1.皖北经济技术学校，安徽 临泉 236400) (2.临泉第四中学，安徽 临泉 236400)

近年来随着各类数控机床的普及，CAD/CAM软件应运而生，许多数控编程人员对CAD/CAM软件运用自如，但对机床自带的宏命令望而生畏，而对于一些复杂的零件利用宏程序[1]加工要比利用CAD/CAM软件编制的程序加工方便快捷[2]。例如一回转体工件，其外圆上有多个孔的中心矢量过偏心孔的中心线。该种工件若使用CAD/CAM编程，工作量较大，因为每个孔的深度、角度位置都不一样，所以每个孔都要进行一次编程操作[3]，导致程序冗滞，不利于机床读取和操作员查阅，工件的装夹也很麻烦，并且每个孔位的坐标都要经过人工测量得到。相比之下利用宏程序加工此种工件则要高效得多。利用宏程序可将工件的加工路径用数学公式进行表达，各加工参数一目了然，便于修改，机床读取程序及计算加工路径更迅速，加工时机床不会出现停顿。为此，本文详细叙述了利用机床工作台旋转功能和工作台回转中心与工件坐标系之间的关系对矢量过偏心孔中心的多个外周孔工件加工的宏程序进行编制(FANUC系统)[4-5]。利用此宏程序，操作人员可以把回转体工件装夹在工作台的各区域内，只需要一个坐标系就能完成对工件外周径向孔的钻削、铣削加工。

1 回转体工件偏心孔中心坐标与工作台回转中心坐标的几何关系

例如要对图1所示工件的外周径向孔进行加工，首先确定工件坐标系与工作台回转中心的关系，然后在工作台旋转后，利用工件和工作台之间的位置关系计算出各外周径向孔的新坐标点。

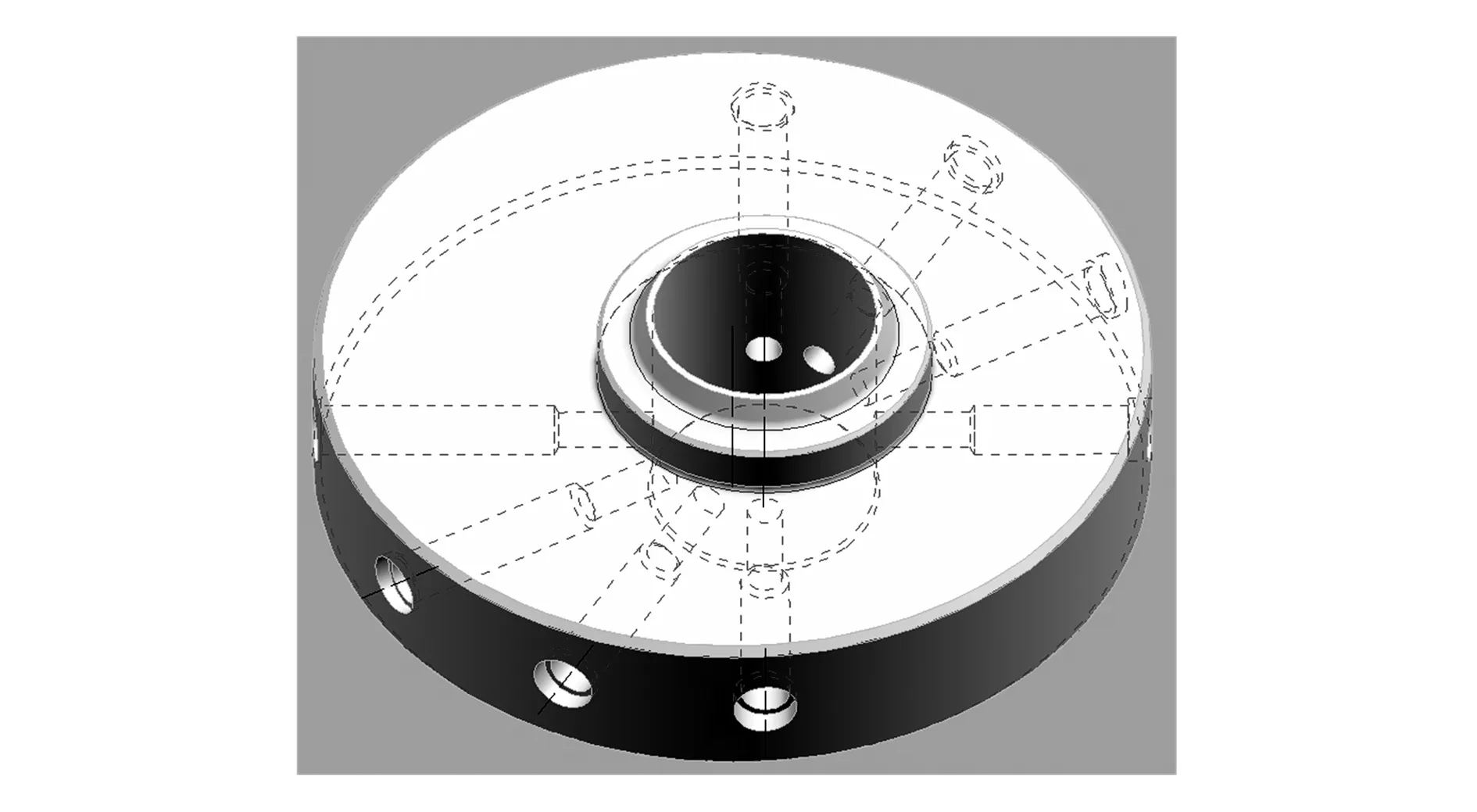
图1 矢量过偏心孔中心线的外周径向孔工件

1.1 工件偏心孔中心与工作台回转中心相对位置的测量

1)转动工作台(B轴)，校正工件的工艺面E，使工艺面E与X轴平行，如图2所示，然后把当前B轴的机械坐标值输入到工作台回转中心的坐标系内，可用不常用到的扩展坐标系G54.1 P48。有些机床工作台回转中心的机械坐标点设置为(0,0,0)，有些机床工作台回转中心的机械坐标点设置是其他数值，比如(500,500,0)。编程员可以查机床参数，也可以自己测量工作台回转中心的X值、Z值，并输入到工件坐标系G54.1 P48内。

2)在机床MDI(manual data input)模式下运行程序(G90 G54.1 P48B0),调出工作台回转中心坐标系G54.1 P48，并使工作台旋转到当前工件坐标系下的B0位置。机床会显示G54.1 P48的绝对坐标系。

图2 工件的工艺面D、E

3)从机床刀库调出分中棒或探头装到主轴上，主轴旋转，在工件坐标系G54.1 P48下工作台B0的位置，对工件偏心孔外壁(如图2所示工艺面D)进行分中，测得工作台B0位置时工件偏心孔中心相对于工作台回转中心的距离a(机床显示器坐标界面绝对坐标的X值，如图3中所示的a)。然后把工作台旋转到工件坐标系G54.1 P48下B270的位置，对工件偏心孔外壁(如图2所示工艺面D)进行分中，测得B270时工件偏心孔中心相对于工作台回转中心的距离b(机床显示器坐标界面绝对坐标的X值)，当工作台在B0位置时，b即是工件偏心孔的中心坐标点相对于工作台回转中心坐标点的Z向差值(如图3中所示的b)。

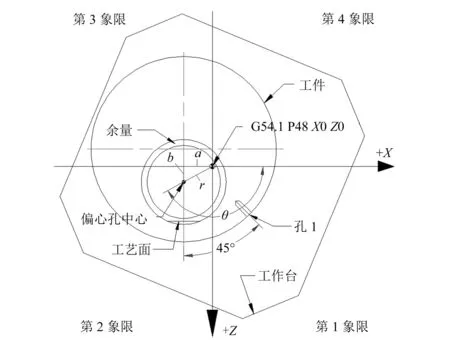
图3 工件坐标系G54.1 P48下工作台B0位置

1.2 工件偏心孔中心相对于工作台回转中心的直角坐标转变为极坐标

根据勾股定理计算工件偏心孔中心相对于工作台回转中心的极坐标半径r：

根据三角函数反函数可以计算出工件偏心孔中心相对于工作台回转中心的极坐标角度值θ：

θ=arctan[b/a]

例1：a=-34.641mm，b=20mm，使用FANUC系统宏程序计算工件偏心孔中心的极坐标。

编写FANUC系统宏程序为：

#101= -34.641； //把公共变量#101赋值a

#102=20； //把公共变量#102赋值b

#104=ATAN[#102]/[#101]； //计算出极坐标角度θ=150°

#105=SQRT[POW[#101,2]+POW[#102,2]]；//计算出极坐标半径r=40mm，在FANUC系统中SQRT是平方函数，POW是次方函数

1.3 工作台B轴旋转后工件偏心孔中心相对于工作台回转中心的直角坐标系

工作台旋转45°后(图4 所示的工作台位置)，r值不变，θ在工作台转动后变为θ1，编程人员可以利用三角函数计算出工作台旋转后工件偏心孔中心相对于工作台回转中心的直角坐标点(a1，b1):a1=rcosθ1,b1=rsinθ1。

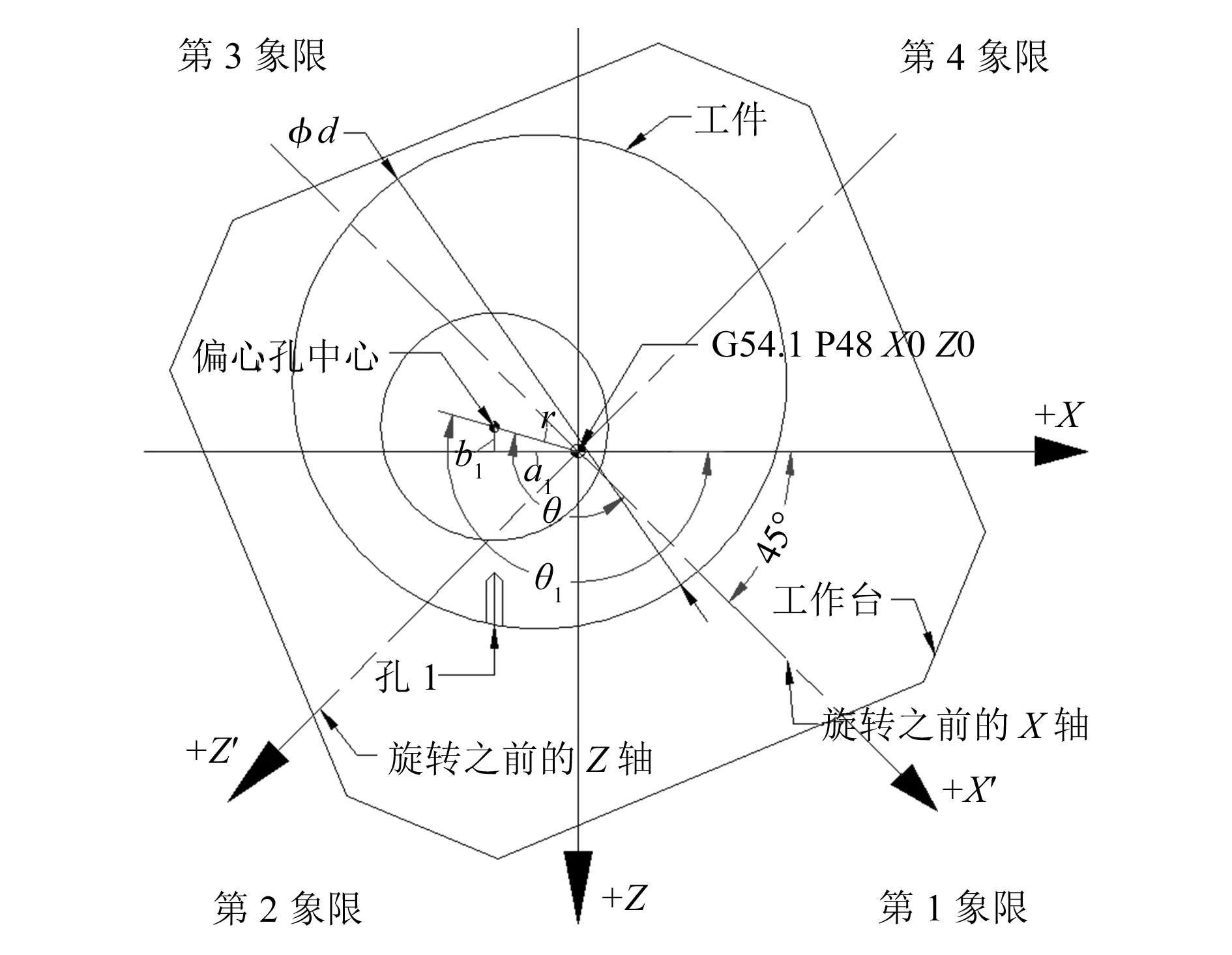
图4 工作台B轴旋转45°后位置

例2：a=-34.641mm，b=20mm ,B轴旋转45°时，使用FANUC系统宏程序求a1，b1。

编写FANUC系统宏程序为：

#4=cos[#104+45]*#105 //#4=a1，θ=#104,θ1=θ+45

#5=sin[#104+45]*#105； //#5=b1

2 孔位的坐标点计算方法

2.1 外周径向孔口中心点到偏心孔中心的距离

如图5所示，在工件的外圆上有孔1，在坐标系G54.1 P48下工作台B0位置时，孔1的孔心矢量与Z轴的夹角为θ2，并且孔的方向矢量过工件偏心孔中心，偏心距为e，工件外圆半径为d/2，求孔1坐标点到偏心孔中心的距离r2(r2随外圆孔角度θ1的变化而变化)。

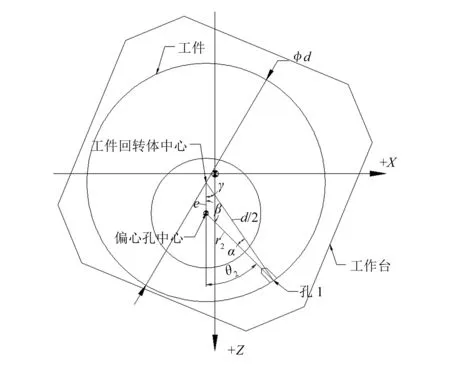
图5 工作台B0位置

在边长为e,d/2,r2的三角形中，与e边所对的角为α，与d/2边所对的角为β，与r2边所对的角为γ。

由补角定理可得：

β=|180°-|θ2|| (-360°≤θ2≤360°)

根据三角形的正弦定理：

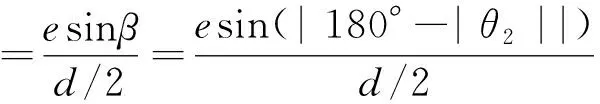
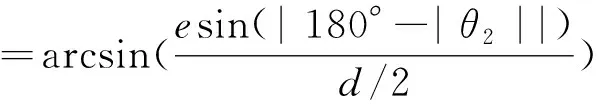
由α+β+γ=180°,得：

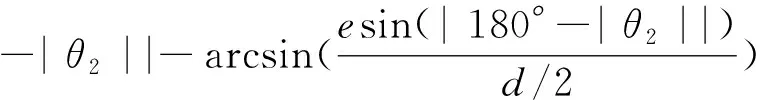
又由三角形余弦定理可得：

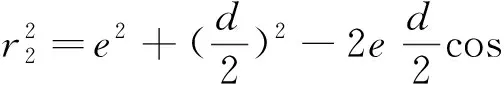
通过以上计算可以得到外周径向孔口中心点到偏心孔中心距离r2的值，用FANUC系统宏程序表示r2值：

#6=180-ABS(180-ABS(#3))-

ASIN( #108*SIN(ABS(180-ABS(#3)))/#103)；

#7=SQRT(POW(#108,2)+POW(#103,2)-2*#108*#103*COS(#6))； //#7=r2，#103为工件半径，#3为孔角度，#108为偏心距e，#6为图5中角γ值，ABS是绝对值函数

在G54.1 P48的坐标系内孔的X轴向坐标为a1，Z轴向坐标为(b1+r2)，即外周径向孔口中心点坐标为(a1，b1+r2)，通过上文示例可知a1=#4,b1=#5,r2=#7，所以外周径向孔口中心点坐标用FANUC系统宏程序参数表示为(#4,#5+#7 )。

例3：如图5所示，工件直径为d，偏心距为e，孔角度为θ2，孔1底部距偏心孔中心距离为100mm，要加工孔1。

编写宏程序为：

#6=180-ABS(180-ABS(#3))-

ASIN( #108*SIN(ABS(180-ABS(#3)))/#103)；

#7=SQRT(POW(#108,2)+POW(#103,2)-2*#108*#103*COS(#6))；

G81 X#4 Y_ Z[#5+100] R[#5+#7+3] F_；

2.2 外周孔坐标用FANUC宏程序格式写法的简化

为了使数控操作者在修改或阅读程序时一目了然，可以把坐标系偏移到孔位上，建立新的坐标系，使用可编程参数输入指令G10进行操作[6]。G10格式如下；

G90 G10 L2 P0 X_Y_Z_；

在FANUC系统中，G90是指绝对偏置，L2是指偏置坐标系，P0是指偏置外部坐标系EXT。

因此例3的宏程序还可以写为：

#6=180-ABS(180-ABS(#3))-ASIN( #108*SIN(ABS(180-ABS(#3)))/#103)；

#7=SQRT(POW(#108,2)+POW(#103,2)-2*#108*#103*COS(#6))；

G90 G10 L2 P0 X#4 Y_ Z[#5+#7]；

G81 X0 Y__ Z[-#7+100 ] R3 F__；

3 应用举例

如图6所示，工件直径为600mm，e为32mm，外圆分布8个过回转体偏心孔中心的台阶孔，工件通过工艺面校正后，偏心孔中心与工作台回转中心在X向的差值是30mm，在Z向的差值是40mm。要加工台阶孔底部距偏心孔中心为150mm的孔。

零件加工宏程序为：

%；

#101=30；

#102=40；

#103=600/2； //#103为工件半径

#104=ATAN[#102]/[#101] ；

#105=SQRT[POW[#101,2]+POW[#102,2]]；

#108=32； //#108为偏心距e

G54.1P48G15G90G00X0Y0S800M03；

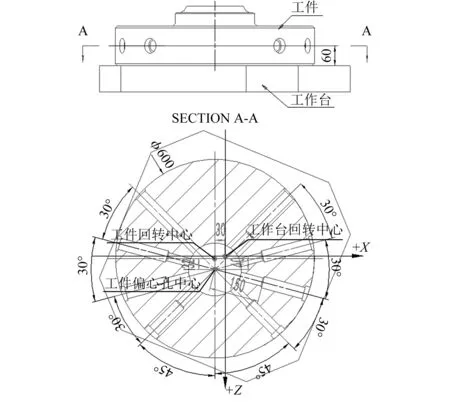
图6 零件图

#3=45； //第一个孔位角度赋值

#2=315； //最后一个孔位角度赋值

WHILE[#3LE#2] DO01；

#4=COS[#3+#104]*#105；

#5=SIN[#3+#104]*#105；

#6=180-ABS(180-ABS(#3))-ASIN( #108*SIN(ABS(180-ABS(#3)))/#103)；

#7=SQRT(POW(#108,2)+POW(#103,2)-2*#108*#103*COS(#6))；

G90B#3；

G90G10L2 P0 X#4 Y150 Z[#5+#7]；

G43H1Z200；

G81X0Y150Z-0.1R2F100；//此段钻孔程序也可换成铣孔程序

G80 G00 Z200；

#3=#3+30； //计算下一个孔的角度

IF[#3EQ165]THEN#3=225；

END01；

；

4 结束语

通过示例可以看出，本文利用工作台的回转中心坐标与工件偏心孔的中心坐标关系，编制宏程序用来加工矢量过偏心孔中心的外圆径向孔是非常方便的，工件装夹不需要定位工装，工件夹紧后，只需要确定工件偏心孔中心和工作台的位置偏差就可以利用程序进行矢量过偏心孔中心的外圆径向孔的孔位坐标计算，进行孔的钻削、铣削加工。此方法还可以扩展到斜孔加工、矢量过回转体中心的外圆均布孔的加工。实践证明，利用此种方法编制的宏程序加工出的零件都符合图样要求，解决了大型工件校正难的问题，减少了工艺员和操作者的工作量，提高了生产效率，加快了生产进程，给企业带来了一定的经济效益。