输气管道泄漏声波衰减模型的理论研究

刘翠伟， 敬华飞， 方丽萍， 徐明海

(1. 中国石油大学 储运与建筑工程学院，山东 青岛 266580； 2. 钦州学院 石油与化工学院，广西 钦州 535011)

目前可以应用于油气管道的泄漏监测方法有许多种，根据所检测的参数不同，主要分为质量/体积平衡法、应用统计法、负压波法、瞬态模型法、分布式光纤法和声波法等。其中，声波法具有诸多优点：灵敏度高、定位精度高、误报率低、检测时间短、适应性强等。根据传感器的不同声波法又可以分为音频法(微型传声器或者麦克风)、振动检测法(加速度计)和动态压力波法(动态压力传感器)。根据目前的研究成果来看，研究主要集中于音频法和振动检测法，二者对短距离管道具有非常好的泄漏检测及定位效果，对长距离管道的应用效果亟需改善，而动态压力波虽然也存在信号衰减，但其幅值大，包含频率范围宽，因此在长距离管道具有较好的效果，基于此提出了基于动态压力波的泄漏监测技术。

国内外学者对声波法泄漏检测与定位技术开展了大量的工作和研究[1-2]。但现行的声波法泄漏检测与定位理论对动态压力波的传播特性研究较少，声波传播特性决定声波传播距离以及传感器采集信号的声波波形，前者决定传感器的安装距离，后者用于计算时间差，进而用于泄漏定位。因此，声波的传播特性对声波法的泄漏检测与定位具有重要的意义，而目前研究的缺乏使得声波法的基础性、通用性、可靠性大大降低，限制了声波法的推广和应用。

声波传播规律的研究可以确定声波的有效传播距离[3]，进而合理布置传感器位置，从而为声波法的工程应用提供支撑。

针对气体管道声波传播规律的研究， Hunaidi等[4]对塑料水管道泄漏信号的声波特征进行了研究。研究包括声波频谱的特征或者作为泄漏类型函数的振动信号，流速，管道压力和时节，衰减率的确定和传播速度的变化；Muggleton等[5-6]针对充液圆管道中泄漏引起的声音和振动波的传播行为进行了机理分析，推导出介质中充液管道的声振耦合系统的频散效应，建立了充液管道中信号的传播模型，并对比分析了检测目标(声波信号)所关注的流体媒质波和壳体波波数的变化情况及衰减特性；刘敬喜等[7]研究了弹性介质中充液管道的波衰减特性，利用壳体基本方程，推导出处于弹性介质中的充液管道在轴对称振动下声振耦合系统的频散方程，利用数值解法得到了频散方程的完全解；孙立瑛等[8]分析了声发射波在液体作用下管道中的声学特性，并对钢管中的几种模态的声发射波在液体管道中的传播和衰减特性进行了测量。Kim等[9]利用时频联合分析的试验方法及边界元法得到了管道系统的声波的截止频率，从而获得管内声波的传播特性。Prek[10]提出了一种利用频域分析的方法来确定弹塑性充液管内声波特性的方法，通过三个压力测量设备之间的传递函数来计算声波波数，计算显示声波波数是复数，且与波速和衰减速率有关，传递函数的实部用于求解波数和相速度，虚部与声波的衰减有关。

Mostafapour等[11]模拟了由于泄漏造成的管道振动所产生的声发射，经管壁传播的压力波可以通过安装在管壁上的传感器记录，研究了声波的传播规律，通过理论与实验分析了声波传播理论对高压天然气管道的泄漏监测效果。潘碧霞等[12]对管道泄漏声发射信号进行传播特性研究，可以为工程上进行传感器布设和采集参数确定提供参考依据。介质类型、压力、流量与泄漏孔径对产生的泄漏声发射信号幅值影响较大，对泄漏声发射信号传播衰减规律无影响。应用傅里叶变换和小波包分解等理论方法，分析泄漏声发射信号在传播过程中经过法兰、阀门时的频率变化特征。Jin等[13]研究了管道泄漏声源特性和传播机理，以天然气管道泄漏时的气动噪声为研究对象，建立了声波在管道内的二维传播模型，通过模拟结果与现场试验的比较分析，表明天然气管道泄漏声波的超低频段可在管道内传播较远距离并能被声波传感器所探测，从理论上验证了声波法在天然气管道泄漏监测领域的良好应用前景。胡杨曼曼等[14]考虑了管道泄漏声发射信号既携带系统结构中的某些特征信息(泄漏孔大小和位置等)，同时又有很大的随机性和不确定性，把次声波传感器接受泄漏次声信号的过程比拟为“听”的动作，来研究在油气管道泄漏监测系统中次声波信号传播的规律。将管壁状况检测的声发射检测方法和基于现代信号处理的检漏方法二者结合进行管道泄漏检测和泄漏点的定位。刘翠伟等[15]提出了一种基于声波传播特性的泄漏定位方法，并对其进行了实验研究，该方法对声波传播规律进行了充分研究，得到了时域、频域和时频域特征的衰减规律，得到了声波传播的理论衰减因子以及实验修正因子，研究结果表明，在输气管道中泄漏声波的衰减遵从指数规律。

针对输气管道泄漏声波传播规律的研究，先建立理想介质中的声波传播公式，然后分析黏滞吸收作用和热传导作用对声波衰减的影响，进一步分析气体流动对声波衰减的影响，并得到湍流对声波衰减的影响，最后建立考虑各种影响因素的声波衰减模型。并采用实验方法对建立的理论模型进行验证，最后得到泄漏声波的传播规律。

1 声波衰减模型的建立

1.1 理想介质中声波传播公式

本文首先推导了输气管道内理想流体介质中的声波传播公式，即一维声波的波动方程

(1)

式中：p为声压;c0为空气中声速。在三维空间内，声波的波动方程为

(2)

按照波阵面的不同，声波可以分为球面波、柱面波和平面波三类。平面波指的是声波沿一个方向传播，在其余方向上所有质点的振幅和相位均相同的声波，它的波动方程即为一维声波方程。

因此式(1)关于平面波的声压解，其表达式为

p(x)=paej(ωt-kx)

(3)

式中：pa为声压振幅;ω为角频率，ω=2πf；k为波数或者传播常数。

在管内可以产生理想的平面波，声压解为

pmm=Ammcos(mθ-φm)Jm(kmnr)ej(ωt-kzz)

(4)

这里的式(4)为方程式(2)的一个特解， 且对应一个m=0，n=0的波，称为(0，0)次波，声压表示为

pmn=Amnej(ωt-kz)

(5)

表1 波数取值表Tab.1 Value of wave number

通过表1可得圆管中平面波的截止频率为

(6)

根据式(6)，对于实际天然气管线，分别计算其平面波的截止频率，得到表2。

表2 天然气管线平面波截止频率Tab.2 Cut-off frequency of plane wave in natural gas pipelines

通过表2可以得出，对于实际管线，当管径达到 1 219 mm时，频率小于163.4 Hz时声波在管内传播模式为一维平面波，在泄漏声波信号传播规律的分析中，典型感兴趣的是可以远传的0～20 Hz甚至是更低频段的信号，因此，在有用信号频段内，输气管道内传播的声波均为一维平面波，其传播模式可以通过式(5)来描述。

通过以上分析明确了在静止无黏的管道流体内，小振幅声波是以一维平面波形式传播的，且在考虑反射波的前提下，其传播方程(1)的解的形式满足

p(x,t)=[C1e-jkx+C2e+jkx]ejωt

(7)

式中： 等式右边第一项为前行波，第二项为反射波，k=ω/a0=2π/λ，λ为波长。 常数C1和C2由声源边界条件和介质特征共同决定。

1.2 黏性静止流体中的平面波衰减

同时考虑黏滞吸收和热传导吸收，得到黏热吸收造成的声波衰减公式，则波动方程的解(7)变为

p(x,t)=[C1e-jkx-αx+C2e+jkx+αx]ejωt

(8)

得到了考虑切变黏滞吸收、容变黏滞吸收和热传导吸收的黏热衰减系数，表达式为

(9)

式中：r代表管径；c0为传播速度；ω为角频率，ω=2πf，f为频率；η为动力黏滞系数；η′为切变黏滞系数；η″为容变黏滞系数；χ为热传导系数；Cv为定容比热；Cp为定压比热。η、χ，Cv，Cp为气体本身的物性参数，主要受温度的影响较大，而随着压力的变化关系较小，因此主要考虑温度对各个量的影响。

1.3 无黏流动流体中的平面波衰减

声波传播是介质惯性和弹性联合作用的结果，因此声波传播是相对于介质而言的。当介质本身以均匀流速U运动时，声波的传播速度相对于介质为a，则相对于静止的坐标系，前行波将以绝对速度U+a传播，反射波将以绝对速度U-a传播，称之为声波被均匀流携带。在短管内，当气体流速的马赫数小于0.3时，可以不考虑气体流动对声波传播的影响，但随着声波传播距离的增加，流动气体对声波衰减的作用累积，不可忽视，很明显的体现为：气体流向与声波传播方向一致时，气流对声波有“携带作用”；当气体流向与声波传播方向相反时，气流对声波有“阻碍作用”。

声波波动方程的广义解为

p(x,t)=[C1e-jω/(a0+U)x+C2e+jω/(a0-U)x]ejωt=
[C1e-jk0x/(1+M)+C2e+jk0x/(1-M)]ejωt

(10)

方程(10)表明，均匀流的携带效应作用于波动方程的两个部分，即前行波和反射波。

1.4 黏性均匀流动介质中的平面波衰减

考虑流体黏度的管中声波波阵面并不是完全的平面波，而是准平面波。同时，气流在管道中的流动速度并不均匀，就同一截面而言，管道中央流速最高，离开中心位置越远，速度越低，到接近管壁时，流速为0。顺流时，管道中央声速高，周壁声速低，逆流时正好相反。根据声折射原理，顺流时，声波要向管道弯曲；逆流时，声波总是要向管道中心弯曲。

根据以上分析，为了解释湍流摩擦造成的额外气动声损失以及均匀流动导致的携带效应，可以将准平面波方程进行拓展，推导等价的一维平面波方程，得到了所需要的在黏性流动气体中的一维声波传播方程。

用下标0表示均匀状态， T代表总状态(扰乱态)，能够写出

ρT=ρ0+ρ;pT=p0+p;uT=U+u

(11)

对小振幅情况

(12)

因此，声波动参数p，ρ和u中包含二次项的项都可以忽略。将这些关系式代入质量连续性方程得到

(13)

从这个方程减去不存在扰动的稳态流动方程，得到

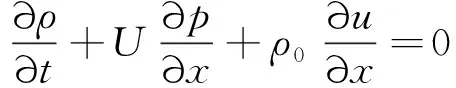
(14)

因此考虑黏热扩散和湍流摩擦的一维动量方程可以表达如下

(15)

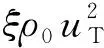
对流体介质中的小振幅波传播，得到声波波动方程

(16)

这个方程与加入了均匀流的携带效应项和流声之间的摩擦项。假设解的形式如下

p(x,t)=Cejωteβx

(17)

将式(17)代入方程式(16)，考虑以下的数量级

M2α2<α2≪k2,ξ2M4<ξ2M2≪k2,
2ξM2α<2ξMα≪k2

(18)

经过代数处理，可以得到

(19)

因此，方程式(16)的解为

(20)

方程式(20)清楚地显示：

(1) 在黏性流动介质中的声波衰减是黏热效应和湍流摩擦共同作用的结果；

(2) 代表均匀流动携带效应的因子1±M作用于衰减系数和波数。

衰减系数表达为

(21)

(22)

式中：α(M)=α+ξM，k=k0+α。α(M)在声波传播的两个方向保持一致，代表流动介质中声波衰减系数的真实值。 1±M在中α±仅代表均匀流产生的多普勒效应。

值得一提的是，为了得到该声波衰减常数，对上述分析做了相当程度的简化，但是从工程应用的角度，都是有意义的。

1.5 理论衰减模型的建立

由以上分析，建立了考虑气体流动、湍流效应和黏热效应的声波幅值的衰减模型，具体如下：

顺向传播

(23)

逆向传播

(24)

对短管道，可以将式(23)和式(24)中的衰减系数简化为

(25)

式中：M越大，代表气体流动对声波衰减的影响越厉害；气流方向与声波传播方向一致时，取“+”，气流方向与声波传播方向相反时，取“-”。

2 声波衰减模型的实验验证

通过10 mm内径管线实验装置进行验证。实验分为两部分：第一部分研究顺流对声波传播和衰减的影响，此时泄漏点1开启，位于下游的传感器2、3、4、5采集信号，且传感器距离泄漏点1的距离分别为0.1 m，48.3 m，109.1 m，160.49 m；第二部分研究逆流对声波传播和衰减的影响，此时泄漏点3开启，传感器4、3、2、1采集信号，传感器4位于泄漏点3下游，其余三个位于泄漏点上游，且传感器距离泄漏点3的距离分别为-0.1 m，60.7 m，108.9 m，151.11 m。每个部分都进行五个压力等级的实验，分别为：1.3 MPa，2 MPa，3 MPa，4 MPa，5 MPa，其中前两个压力等级采样频率为1 000 Hz；后三个压力等级采样频率为3 000 Hz。然后对实验数据进行处理，对顺流和逆流下的衰减因子进行拟合。

通过对实验数据的处理得到了拟合衰减因子，同时采用建立的理论衰减因子公式计算衰减因子，根据式(9)得到了理论黏热衰减因子，根据式(23)得到顺流衰减因子，根据式(24)得到逆流衰减因子。其中采用理论公式计算衰减因子时分别采用原始信号和小波特征进行，原始信号的能量集中于0～50 Hz，因此中心频率为25 Hz，将理论衰减因子与实验拟合的衰减因子相减并除以实验拟合的衰减因子得到误差。原始信号处理结果具体见表3。

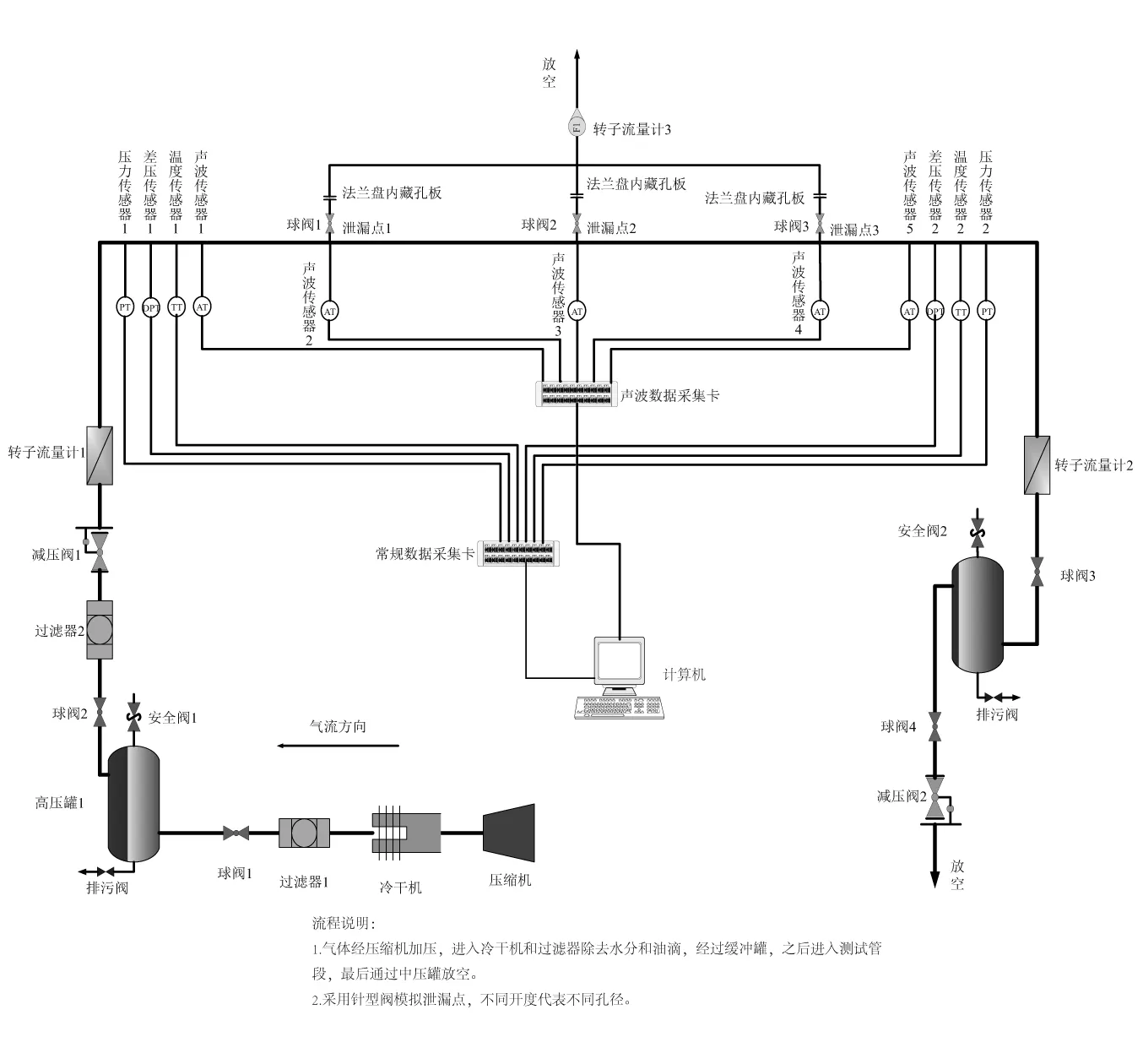
图1 高压输气管道声波泄漏检测与定位装置Fig.1 High pressure gas pipeline leak detection and location device based on acoustic method

由表3可知：

(1) 与实验拟合值相比，顺流时误差都较小，都在6.0%以内，且实验拟合衰减因子基本都大于理论衰减因子。

(2) 与实验拟合值相比，逆流时误差随压力增大而增大，且实验得到的拟合衰减因子基本都大于理论衰减因子，且误差较大。

(3) 这主要是由于实验时气体流速并不是单一值，而理论计算时采用的平均值，若实验中变化的气体流速产生的总作用大于平均流速下的气体流动产生的总作用，就会出现实验拟合衰减因子大于理论衰减因子的情况。为减小误差，需对管道中的气体流速进行布点准确测量。

同时对小波特征进行了处理，得到了基于小波特征的声波传播衰减因子，其中采样频率为1 000 Hz的信号选定A4子带，中心频率为15.625 Hz；采样频率为3 000 Hz的信号选定A5子带，中心频率为23.437 5 Hz，计算结果见表4。

表3 原始信号理论衰减因子与实验拟合衰减因子误差Tab.3 The attenuation factors errors of the original signals in the same direction

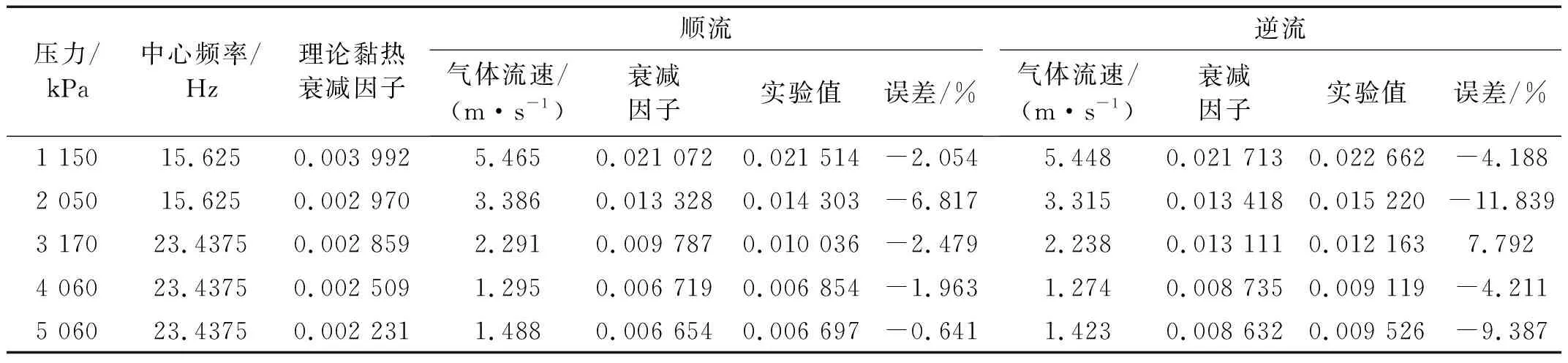
表4 小波特征顺流理论衰减因子与实验拟合衰减因子误差Tab.4 The attenuation factors errors of the WT signals in the same direction

由表4可知，采用小波特征计算得到的衰减因子的变化规律为：①与实验拟合值相比，顺流时误差都较小，都在7.0%以内，且实验拟合衰减因子都大于理论衰减因子；②与实验拟合值相比，逆流时误差也都在12%以内，且实验得到的拟合衰减因子基本都大于理论衰减因子。原因与原始信号基本一致。

误差来源于：①管道中存在弯管、阀门等附件，使得声波产生发射和散射，从而使得声波幅值的衰减规律并不完全服从指数规律；②所提取的声波幅值的不准确性，主要由原始信号采集的不准确性和信号处理的限制造成，同时原始信号采集的不准确性来源于传感器的精度和采样频率的限制。为解决这一问题，可以选择精度更高的传感器同时设置较高的采样率，传感器精度越高，采样频率越高，传感器所采集的信号的准确性越高，但是由于采样率越高，所需要的中控计算机的内存越多，方法实施所需要的成本越高，因此需要选择适当的传感器同时设置适当的采样频率。信号处理的误差主要来源于小波变换在提取声波幅值的过程中造成的幅值损失，为解决这个问题需对信号处理方法进行进一步改进。③定位误差还来源于实验操作，实验中泄漏是通过阀门开启实现的，虽然操作过程中尽量模拟实际中的泄漏工况，但误差难免存在，造成产生信号数据的浮动。同时在实验衰减因子的拟合过程中也存在误差。

通过实验结果验证了所建立的理论衰减模型的准确性。

3 结 论

为研究泄漏声波在输气管道中的传播规律和衰减模型，从理论研究出发建立了声波幅值衰减模型，且从实验研究出发对声波幅值衰减因子进行了拟合，验证了声波幅值衰减模型，得到主要结论如下：

(1) 从理论上建立了黏性均匀流动介质中考虑气体流动、湍流效应和黏热效应的声波幅值衰减模型，尤其是顺流情况和逆流情况下的衰减因子表达式。

(2) 通过实验和理论计算得到了10 mm气体管线顺流和逆流情况下的衰减因子。采用原始信号计算得到的衰减因子的变化规律为：与实验拟合值相比，顺流时误差都较小，都在6.0%以内，且实验拟合衰减因子基本都大于理论衰减因子；逆流时误差随压力增大而增大，且实验得到的拟合衰减因子基本都大于理论衰减因子，且误差较大；采用小波特征计算得到的衰减因子的变化规律为：顺流时误差都较小，都在7.0%以内，且实验拟合衰减因子都大于理论衰减因子；逆流时误差也都在12%以内，且实验得到的拟合衰减因子基本都大于理论衰减因子。