循环载荷下煤样不同方向渗透特性试验研究*
贾立锋,董 擎,梁 冰,孙维吉
(1.辽宁工程技术大学,矿业学院,辽宁 阜新 123000;2. 安阳工学院,机械工程学院,河南 安阳 455000;3. 辽宁工程技术大学,力学与工程学院,辽宁 阜新 123000)
0 引言
在煤层开采过程中,部分煤体受到采动应力的反复作用,例如分层开采的下伏煤层,起支撑和隔离作用的煤柱、反复水力压裂的煤体等。煤体内含有大量的孔隙裂隙,循环载荷作用下煤体内部结构会发生变化,影响煤体的渗透特性。煤是一种典型的沉积岩,具有各向异性的特征[1-3],循环载荷作用下煤体不同方向的渗透情况均会发生变化。
目前循环载荷作用下煤体渗透的研究有很多[4-7]。潘荣锟等[5]对含层理原煤开展了渗透实验,结果表明随着有效应力的增大,渗透率降低,加载过程中煤体层理裂隙变形对裂隙面造成永久性损伤;魏建平等[6]开展了不同含水率条件下2次卸载围压的三轴渗流实验,第2次加载过程中渗透率较第1次平缓,2次卸载过程中,渗透率有一定程度升高,但恢复不到初始值;郭军杰等[7]以原煤为研究对象,进行等幅循环加卸载的渗透率测试,得到在渗透率降低阶段,渗透率与循环次数呈幂指数函数关系,在渗透率升高阶段,渗透率与循环次数呈指数函数关系。在煤渗透各向异性的研究方面[8-11],王登科等[8]开展了含瓦斯煤的各向异性渗流规律的研究,结果表明,煤体瓦斯流动具有非常明显的各向异性特征,其渗透率与有效应力之间符合负指数函数变化规律;田坤云等[9]对加卸载过程平行、斜交及垂直层理方向的原煤试件进行了渗透实验,研究表明,加载过程中煤样的渗透率与有效应力成正比,卸载过程中渗透率与有效应力之间成反比;赵宇等[11]在不同围压和气体压力下对煤样的面割理、端割理、垂直层理方向上的渗透率进行测试分析,研究认为不同气体压力下渗透率随着围压增大而减小,气体压力对端割理方向和垂直层理方向渗透率影响不大。
上述研究仅考虑了煤的各向异性渗透特征或者循环加载条件下单个方向的渗透特征,未将二者结合起来。本文以平顶山十二矿己15煤层煤样为研究对象,利用自行研制的应力-渗流-解吸煤体变形试验装置,研究了循环围压加载下煤样不同方向渗透特征。
1 试验方法
1.1 试样的制备
煤样取自于河南省平顶山十二矿己15煤层,取样地点在31030工作面进风巷,屈服强度2.44~ 2.62 MPa,抗压强度为4.86~6.37 MPa。将煤样采集回来后,判断煤的层理方向和裂隙发育情况,用岩石切割机制作尺寸为50 mm×50 mm×50 mm的层理方向正方体试样,如图1所示。尽可能避免试样内含有裂隙,最后用ZDM-200磨石机进一步加工煤块,保证试样的边长为50±1 mm。

图1 试样及其层理结构特征Fig.1 Specimens and bedding structure characteristics
本试验共加工出2块试样,分别编号为PDS-1B和PDS-2,2块试样的层理面平行于面3,垂直于面1和面2,表面无明显裂纹,而PDS-2试样面1和面2交叉处下方有缺角。
1.2 试验装置
试验使用的是自行研制的应力-渗流-解吸煤体变形试验装置(见图2),该装置详细介绍见文献[12-13],本试验未使用装置中的变形测量系统。为了能够测试试样不同方向的渗透率,给煤样夹持器添加了1个正方体压头。改进前只能测试尺寸为50 mm×50 mm×100 mm的长方体试样,改进后可以对截面积50 mm×50 mm×50 mm的试样进行测试(见图3)。渗透试验采用的气体为纯度99.99%的N2。
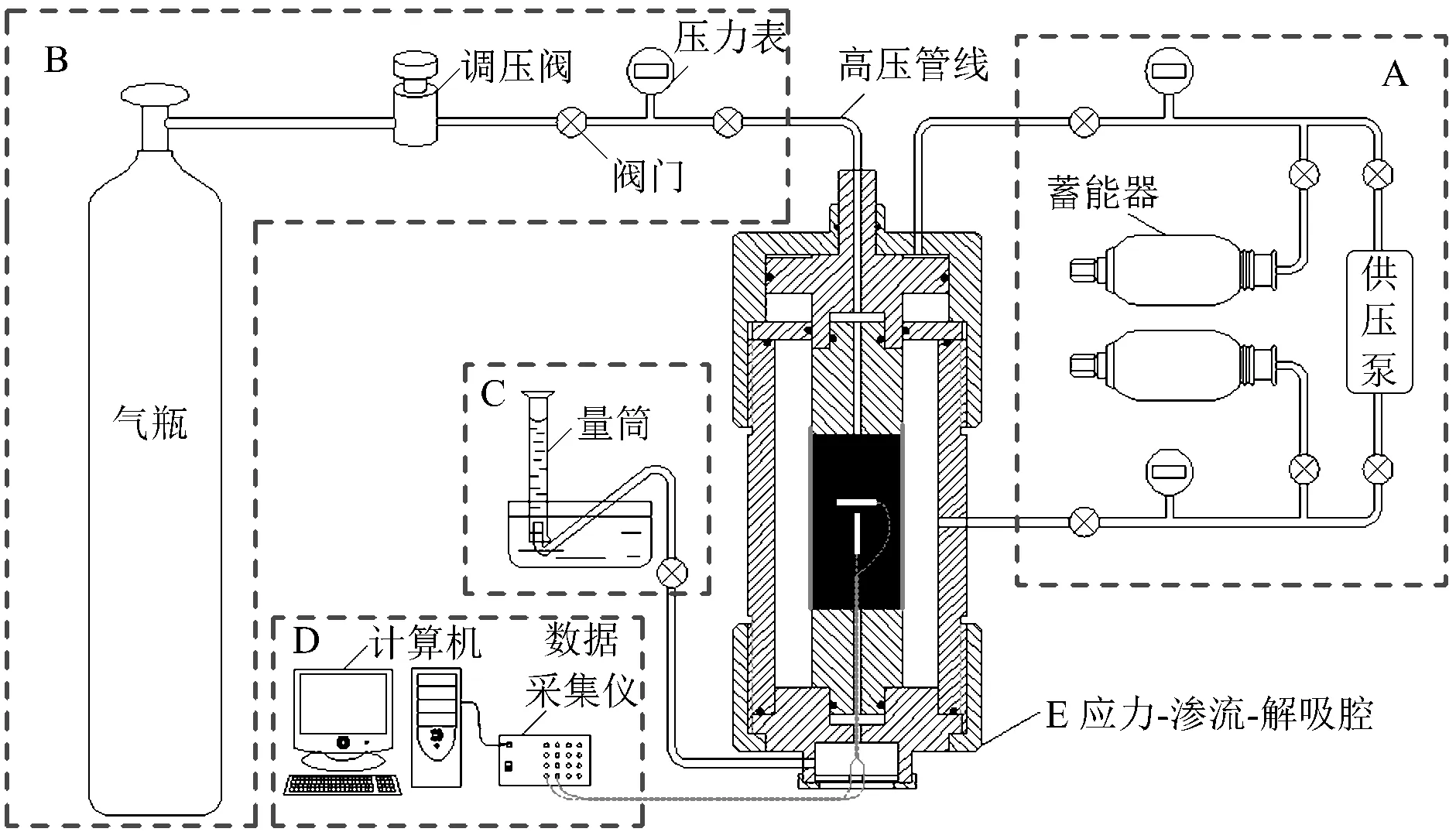
图2 应力-渗流-解吸煤体变形试验装置Fig.2 Experimental device of coal matrix deformation caused by stress-seepage-desorption

图3 夹具中的试样Fig.3 A specimen in the gripper
1.3 试验原理及步骤
渗透率是表征多孔介质渗透特性的重要参数。根据稳态法测试煤岩样渗透率原理,渗透率可以通过公式(1)计算:
(1)
式中:k为煤体的渗透率,m2;pout为煤体出口压力,Pa;pin为煤体进气口压力,Pa;Qout为试样出口稳定流量,m3/s;A为流体通过的截面积,m2;L为煤样的长度,m;μ为氮气的动力黏度,17.58×10-6Pa·s。
试验研究循环载荷作用下煤样不同方向上渗透特性,需要对试样的3个面进行测试,测试顺序为垂直于面1方向、垂直于面2方向、垂直于面3方向,每个面测试完毕后依次需要卸载轴压和围压、拆卸试件更换测试面、封装试件、施加轴压、围压。
用PDS-1B试样测试了不同方向渗透的初始值,为了避免围压和轴压对渗透率造成干扰,围压和轴压取值为2 MPa,小于煤体的屈服强度。进气口压力以0.3 MPa为初始值,以0.3 MPa/次的增量加载至1.5 MPa结束。依次测试垂直于面1、面2、面3方向的渗透率。
用PDS-2试样开展循环载荷下煤体不同方向渗透率试验。具体试验步骤如下:1)将试验装置按图2连接,检查试验装置的气密性;2)将PDS-2煤试样依图3方式安装,安装时保证垂直于面1的方向为渗透方向;3)将轴压加载至3 MPa,围压加载至4 MPa,待轴压和围压稳定后加载孔隙压力。进气口压力(相对压力值)以0.5 MPa为初始值,以0.5 MPa/次的增量加载至3 MPa,测试渗流稳定时单位时间内排出气体的体积;4)将围压以1 MPa/次的增量由4 MPa加载至8 MPa,每个围压下均重复步骤3)中进气口压力的加载路径,并测渗流稳定时单位时间内排出气体的体积;5)面1测试完毕后,重复步骤3)~5)对试样的垂直于面2和面3方向的渗透率进行测试。
2 试验结果分析
假设气体压力在试样内均匀分布,试样沿渗透方向的孔隙压力是不断变化的,可以采用进口压力和出口压力之和的平均值来压计算孔隙压力[14],本文以平均孔隙压力pm为指标,分析其与渗透率的关系,如式(2)所示:
(2)
2.1 层理特征对煤体渗透率的影响
对PDS-1B不同方向渗透率测试结果分析可以得到平均孔隙压力与渗透率的关系,如图4所示。
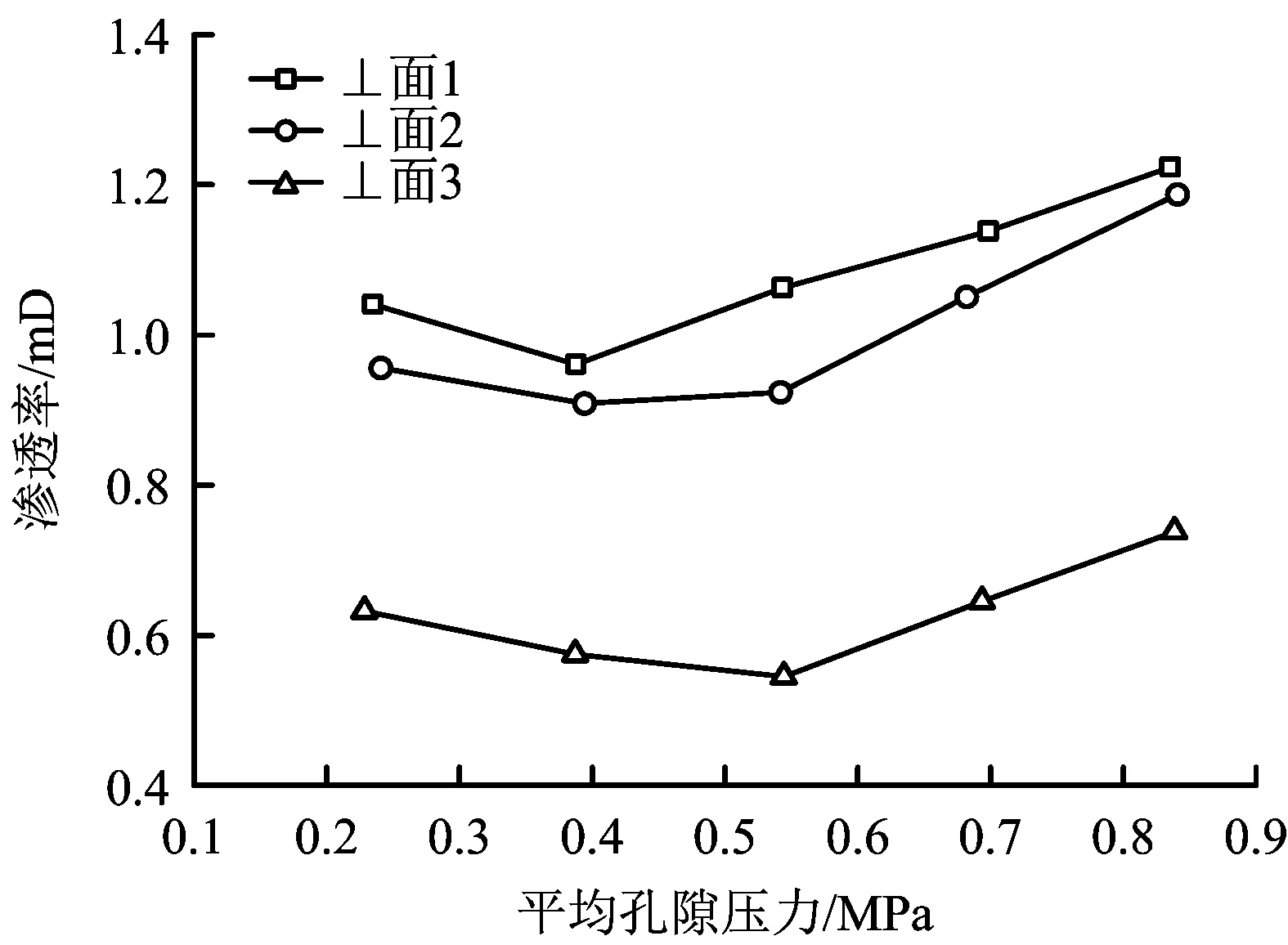
图4 PDS-1B不同方向渗透率随平均孔隙压力变化Fig.4 Variation of permeability in different directions with average pore pressure
由图4可以看出,垂直于面1方向渗透率的范围为0.96~1.22 mD,垂直于面2方向渗透率范围为0.91~1.19 mD,垂直于面1和面2渗透方向为平行于层理面方向,在平均孔隙压力相同时渗透率相差不大。垂直于面3渗透的方向为垂直于层理面方向,渗透率范围为0.54~0.74 mD,小于平行层理面的渗透率。在相同的轴压、围压和平均孔隙压力下,煤在垂直层理面方向的渗透率大于平行层理面,平行层理面内的渗透率相差不大。
2.2 循环载荷下渗透压差与流量的关系
渗透压差是试样进气口和出气口的压力差Δp,由于压力表的读数为相对压力值,出口压力为大气压,因此渗透压差数值上等于进口压力表值。渗透压力与流量的关系如图5所示。

图5 流量与渗透压差之间的关系Fig.5 Relationship between rate of flow and osmotic pressure difference
由图5可以看出,随着渗透压差的增大,通过煤样的流量增加,且二者之间的关系可以用函数Q=D1(Δp2+0.2Δp)表示,其中D1为拟合系数,二次函数拟合出的相关性系数R2均大于0.999。如图5(a)所示,垂直于面1渗透时,围压为4 MPa,渗透压差为3 MPa时流量为26.49 mL/s;围压为5,6,7和8 MPa,渗透压差为3 MPa时流量分别为12.41,8.35,5.30和4.11 mL/s,在相同渗透压差下,通过试样的流量随着围压的增大而减小。如图5(b)所示,垂直于面2渗透时,该方向流量随压差的变化规律与垂直于面1方向相同,但在相同围压和渗透压差下,垂直于面2方向上通过试样的流量大于垂于面1方向。垂直于面3渗透时,在相同渗透压差下,围压对透过试样流量影响比较复杂,在渗透压差为1 MPa时,Qσ3=6 MPa>Qσ3=8 MPa>Qσ3=4 MPa;渗透压差为2 MPa时,Qσ3=6 MPa>Qσ3=4 MPa>Qσ3=8 MPa。其原因可能是围压为6 MPa时,试样内有新裂隙产生,流量增大,而围压由6 MPa增加至8 MPa时裂隙闭合。
2.3 循环载荷下平均孔隙压力与渗透率的关系
渗透率与平均孔隙压力之间的关系如图6所示。

图6 渗透率与平均孔隙压力之间的关系Fig.6 Relationship between permeability and average pore pressure
由图6(a)可以看出,垂直于面1渗透时,围压为4 MPa时煤样的渗透率随着平均孔隙压力的增加呈现先减小后增加的趋势,平均孔隙压力为1.6 MPa时的渗透率达到最大值0.196 mD,而围压为5,6,7和8 MPa时煤样的渗透率随平均孔隙压力变化不大;从图6(b)可以看出,垂直于面2渗透时,渗透率随着平均孔隙压力的增大而上下波动,随着围压的增大渗透率逐渐减小,但在相同的平均孔隙压力和围压下,垂直于面2方向的渗透率明显高于垂直于面1方向上的渗透率。垂直于面1和面2方向上渗透率随平均孔隙压力变化不大,渗透率只与多孔介质本身的结构特征有关,与流体特征无关[15]。
从图6(c)可以看出,垂直于面3渗透时的变化规律与垂直于面1和面2时不同,首先渗透率随平均孔隙压力的增大而减小,其规律可以用考虑克林伯格效应的渗透率公式表示:
(3)
式中:k0为试样的绝对渗透率, mD;b为克林伯格系数。围压为4,6,8 MPa时的曲线拟合相关性系数分别为0.864,0.945,0.964,拟合度较高。说明垂直于面3渗透时,渗透率受克林伯格效应的影响。其次,相同渗透压差下,随着围压的增加,渗透率变化规律复杂,和围压对透过试样流量的影响类似。
2.4 循环载荷对不同方向渗透率的影响
将同一围压不同平均孔隙压力下的渗透率视为1组数据,求出其算数平均值。将PDS-1B在围压2 MPa时的算术平均值作为渗透率初始值,其垂直于面1,面2,面3方向的初始渗透率分别为1.085,1.005和0.627 mD。将PDS-2垂直于面1,面2,面3方向的不同围压下渗透率的算术平均值与初始渗透率值比值(下文简称渗透率比值)作为分析指标,建立其与围压的关系,如图7所示。虽然垂直于面3方向渗透率随平均孔隙压力变化很大,为了分析循环围压加载对渗透率的影响,也对其求算术平均值。

图7 不同方向渗透率比值与围压之间的关系Fig.7 Relationship between confining pressure and permeability ratio in different directions
由图7可知,垂直于面1和面2方向为平行于层理方向,初始渗透率在1 mD左右,第1次加载和第2次加载时渗透率比值均小于0.3,这是因为围压增加,导致煤体内裂隙闭合,渗透率变小。在相同的围压下垂直于面3的渗透率比值大于垂直于面2同时也大于垂直于面1的渗透率比值,这是因为循环围压大于煤样的最大屈服强度和单轴抗压强度,煤样内部垂直于面2经历了1次加载,面3经历了2次加载,裂隙得到扩展。说明渗透率比值随循环加载次数的增加而增大。煤的初始渗透率为垂直于面1,面2,面3时的初始渗透率,分别为1.085,1.005和0.627 mD,大小顺序垂直于面1大于垂直于面2,大于垂直于面3,经历3次循环加载后,渗透率比值垂直于面3方向大于垂直于面2,大于垂直于面1。
随着围压的增加,垂直于面1和面2方向的渗透率比值逐渐减小,这是因为围压增加,孔隙裂隙逐渐闭合。垂直于面3方向渗透率比值在围压6 MPa时较大,这可能是由于在围压6 MPa时煤体破坏,较4 MPa时平均渗透率增加,围压为8 MPa时裂隙较6 MPa时闭合,渗透率比值减小。
3 结论
1)在相同的轴压、围压和平均孔隙压力下,平行层理面方向的渗透率大于垂直层理,平行层理面内的渗透率相差不大。
2)通过煤样的流量随着渗透压差的增大而增加,且二者之间的关系可以用Q=D1(Δp2+0.2Δp)表示。
3)PDS-2垂直于面1和面2渗透时,随着平均孔隙压力的增加,渗透率变化幅度不大。垂直于面3渗透时,渗透率随平均孔隙压力的增大而减小,渗透率与平均孔隙压力之间的关系可以考虑用克林伯格效应的渗透率公式描述。
4)围压增加,导致裂隙闭合,渗透率减小,当循环围压大于煤屈服强度和抗压强度时,裂隙扩展,渗透率增加。循环围压加载可以改变煤样原有不同方向的渗透率大小顺序,渗透率与原初始渗透率比值随循环加载次数的增加而增大。

