湍流模型和壁面函数对有障碍半开口空间氢气燃烧模拟的影响*

李丹丹，李 敏，刘松林，罗广南

(1.中国科学院等离子体物理研究所，安徽 合肥 230031；2. 中国科学技术大学，安徽 合肥 230026)

0 引言

氢气是一种重要的清洁能源和化工原料，应用非常广泛，在工业生产中(如核能发电)也可能产生大量氢气。由于氢气易燃易爆，在瞬间产生超压，可能会造成严重的人员伤亡和财产损失，因此，对氢气燃烧过程做出尽可能准确地预测对提高氢气安全性具有重要意义。氢气燃烧可能处于含有设备、管道、支架等类似障碍物结构的非密闭环境中，障碍物对氢气燃烧能量释放[1]和火焰传播[2]具有重要影响，且开口处的泄压使氢气燃烧行为变得复杂[3]。

目前，在有障碍物半开口空间内氢气燃烧方面，Lyu等[4]实验研究了障碍物位置和氢气浓度对氢气-空气混合气体爆炸压力的影响；Porowski等[5]测量了不同障碍物阻塞率、间距和气体组分浓度下的氢气-甲烷-空气混合气体的燃烧压力和速度；Alekseev等[6]在有障碍物开口管道内开展了氢气-空气火焰加速和爆燃爆轰转变(Deflagration to Detonation Transition，DDT )实验；余立新等[7]开展了氢气-空气预混火焰在半开口有障碍物管道中的火焰传播实验研究；Gaathaug等[8]开展了氢气-空气混合气体DDT实验和数值模拟研究；Vyazmina等[9]基于2个不同点火位置的氢气燃烧实验进行了FLACS CFD软件数值模拟验证；Gamezo等[10]利用数值模拟研究了障碍物间距对预混氢气燃烧火焰加速和DDT的影响；Li等[11]评估了不同障碍物位置、数量和间距对氢气燃烧压力的影响；温小健等[12]模拟了不同的障碍物阻塞率和形状等因素下的氢气燃烧火焰传播速度和压力。综上所述，国内外已开展的相关实验和数值模拟研究，主要是为了考察了不同条件下氢气燃烧压力和火焰传播速度，其中数值模拟验证尚不充分，缺少湍流模型和壁面函数对数值模拟准确性影响的研究。

本文基于文献中的实验，利用FLUENT软件研究湍流模型和壁面函数对有障碍物的半开口空间内氢气-空气预混气体燃烧过程数值模拟结果的影响。采用了动态自适应网格加密技术，进行了网格和时间敏感性分析，确定合适的网格尺寸和时间步长，在此基础上采用不同湍流模型和壁面函数，预测了氢气燃烧压力和火焰传播行为，并将数值模拟结果与实验结果进行了对比。

1 实验装置

将有燃烧压力测量数据和火焰传播图像的实验[4]作为对比，从燃烧压力变化和火焰传播行为2个方面考察数值模拟结果的准确性。实验段的基本结构如图1所示，实验段为方形管道，尺寸为100 mm×100 mm×500 mm，底端封闭，顶端用聚氯乙烯薄膜密封。管壁为玻璃材质，以便利用高速相机拍摄火焰图像。点火位置位于底部中心，压力传感器距点火位置20 mm(见图2)。障碍物尺寸为100 mm×50 mm×10 mm，阻塞率为0.5，障碍物距离实验段底部100 mm。

图1 实验段基本结构Fig.1 Schematicdiagram of experiment section

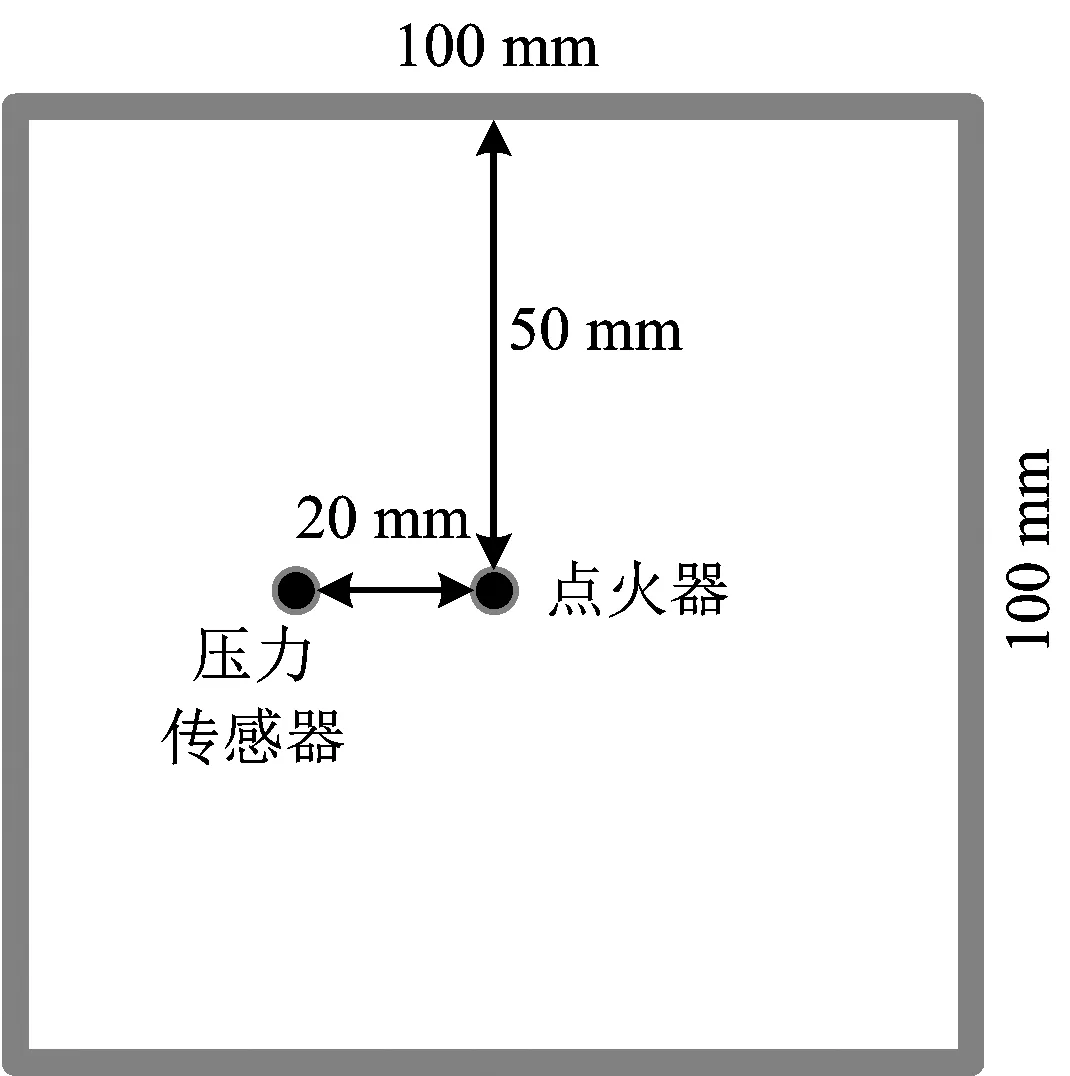
图2 压力传感器位置Fig.2 Position of the pressure sensor

2 数值模拟模型及方法

2.1 几何模型、初始及边界条件

由于实验段具有几何对称性，因此取实验段剖面的1/2建立二维几何模型。几何模型被划分成2 mm的四边形网格，在此基础上采用自适应网格加密技术，在数值计算过程中根据温度梯度变化自动调整网格尺寸，以提高计算精度和效率。实验管段中的气体混合物由氢气和空气组成，其中氢气的体积分数为29.6%。压力监测点位置与文献实验中压力传感器位置一致。氢气和空气在被点燃之前混合均匀并保持静止，初始压力和温度分别为0.1 MPa和298 K。由于燃烧时间很短，实验段的所有壁面被视为绝热，开口端被设置为无反射压力出口边界条件。

2.2 数值模拟方法

采用有限速率/涡耗散燃烧模型，考虑化学反应动力学与湍流混合速率对燃烧化学反应速率的影响[13-14]。压力速度耦合采用SIMPLE算法。忽略燃烧过程中从管内燃烧产物到管壁的热量损失。由理想气体定律确定燃烧过程气体混合物的密度。气体的比热、热导率和粘度被定义为温度的多项式函数。根据文献[15]中的公式计算层流火焰燃烧速度。通过火花点火模型点燃氢气-空气预混气体，假设火花初始半径为5 mm，火花能量为0.1 J，点火持续时间为5倍时间步长。在进行网格和时间步长敏感性分析中，采用标准k-ε湍流模型和标准壁面函数。确定合适的网格尺寸和时间步长之后，考察标准、RNG和可实现k-ε湍流模型对数值模拟结果的影响。在此基础上，选取其中最合适的湍流模型，分析标准、可伸缩和非平衡壁面函数对数值模拟结果的影响。

2.3 网格与时间步长敏感性分析

在网格自适应方案中分别设置网格加密级数为2，3和4，最小网格尺寸分别达到1，0.5和0.25 mm。图3为网格加密级数为2时的火焰面网格，火焰面网格明显比非火焰面区域的更密。

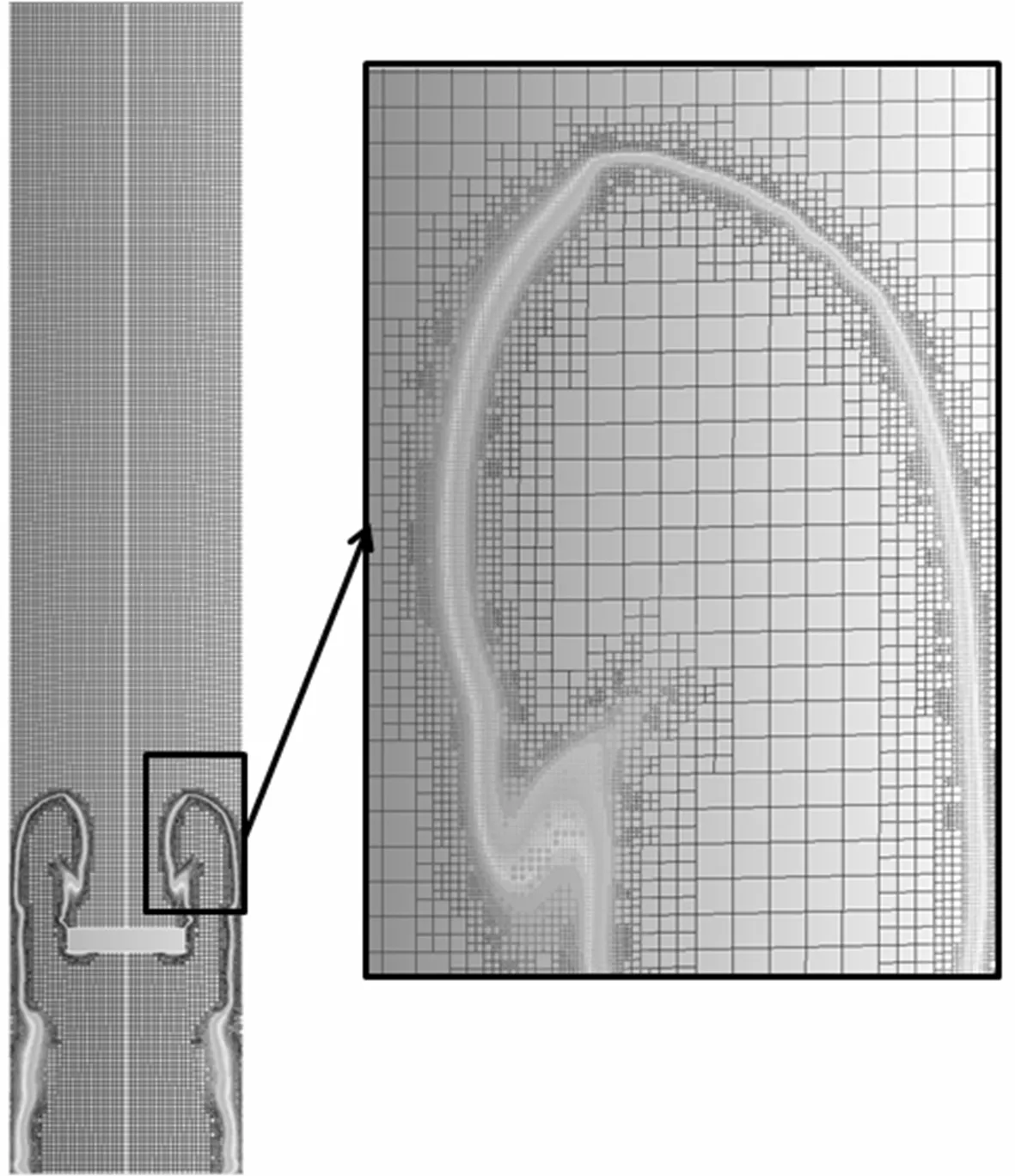
图3 火焰面自适应网格Fig.3 Adaptive mesh of flame front

图4为网格敏感性分析结果，与实验值比较，通过数值模拟得到的压力变化趋势与测量结果都很相似，但压力峰值出现的时间都提前了2 ms左右。数值模拟与实验结果相比存在时间迁移现象，这在相关数值模拟[16-17]中是存在的，可能由在数值模拟中采用的点火半径和初始湍流参数与实际值存在偏差所导致，但并不影响对压力变化趋势和火焰传播行为预测结果准确性的评估。由图4可知，当网格加密级数为2时，能够比较准确地预测出压力变化；当网格加密级数为3和4时，压力峰值均增加，压力曲线接近，说明当网格加密级数大于3时，网格尺寸对数值模拟结果的影响很小。因此，以下采用网格自适应加密级数为3。

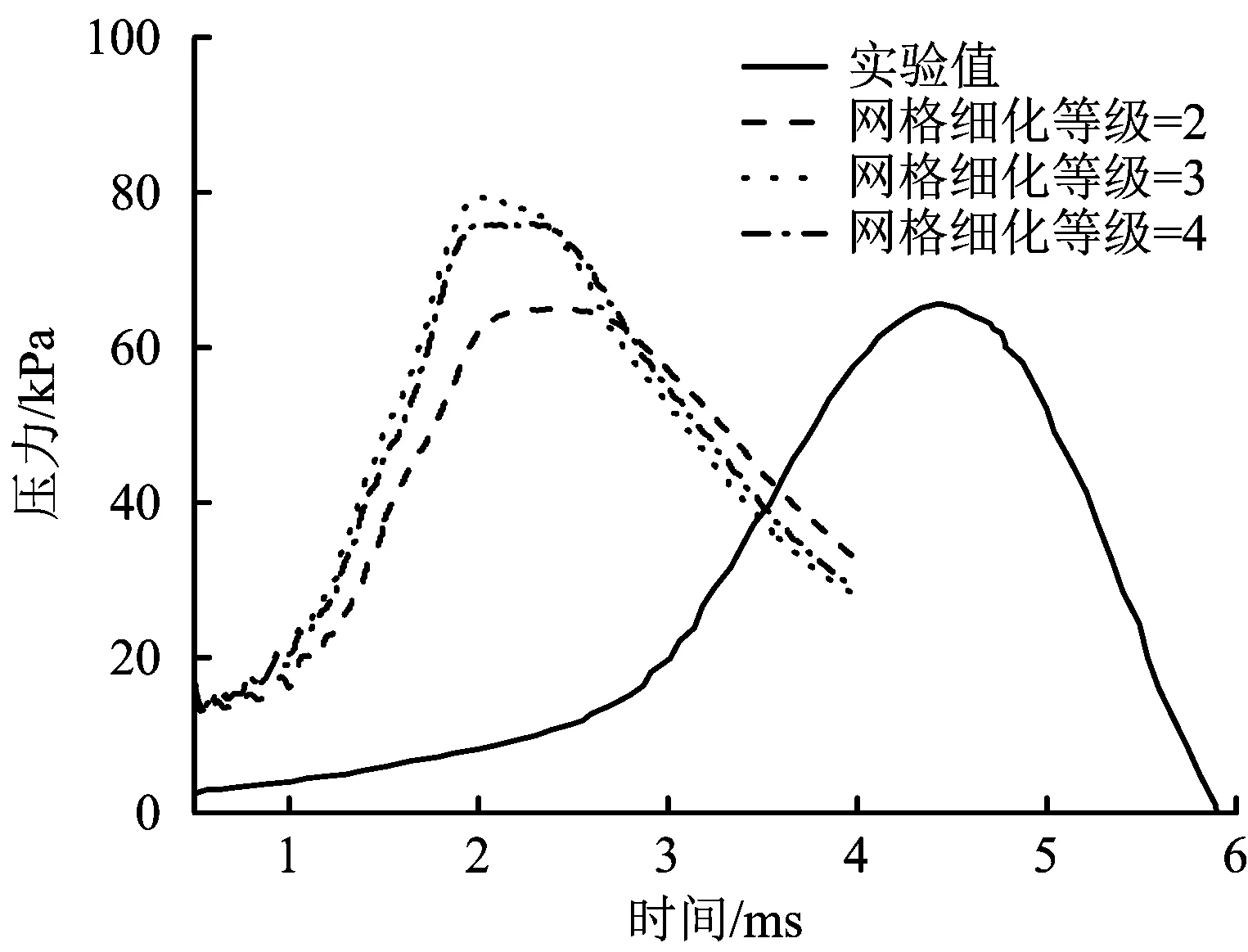
图4 网格敏感性分析Fig.4 Grid sensitivity analysis

在时间步长敏感性分析中，时间步长Δt的范围是4×10-7～5×10-6s，图5为时间步长敏感性变化。由图5可知，当时间步长为5×10-6s和3×10-6s时，压力变化趋势和压力峰值与实验值相差较大，压力峰值比实验测量到的压力值分别小30.2%和10.8%，说明如果时间步长过大，数值模拟结果不准确。当将时间步长设为5×10-7s和4×10-7s时，得到的压力变化趋势很接近，压力峰值仅相差2.4%，因此在以下数值模拟中时间步长都设为5×10-7s。

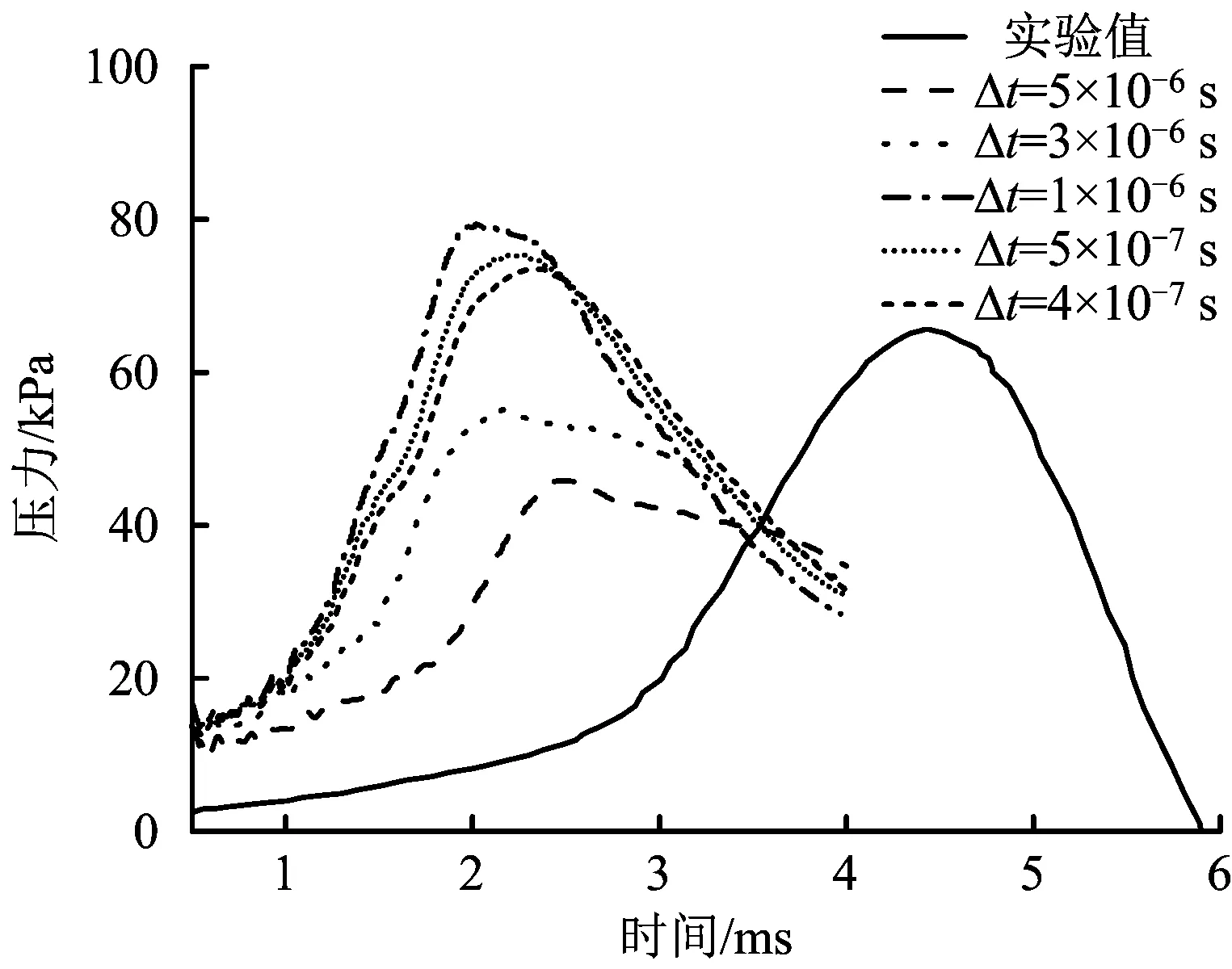
图5 时间步长敏感性分析Fig.5 Time step sensitivity analysis

3 数值模拟结果及分析

3.1 湍流模型对数值模拟的影响

图6为不同k-ε模型对燃烧压力数值模拟结果的影响。其中，可实现k-ε模型对应的压力变化趋势与实验结果偏离程度最大，压力上升速度最快，压力峰值比测量值大51.2%。标准和RNGk-ε模型对应的计算结果比较接近，压力峰值与测量值相比相对偏差分别为14.9%和7.9%，表明由RNGk-ε模型获得的压力峰值与实验值最吻合。并且，采用 RNGk-ε模型所得到压力上升速度与实验值最接近。

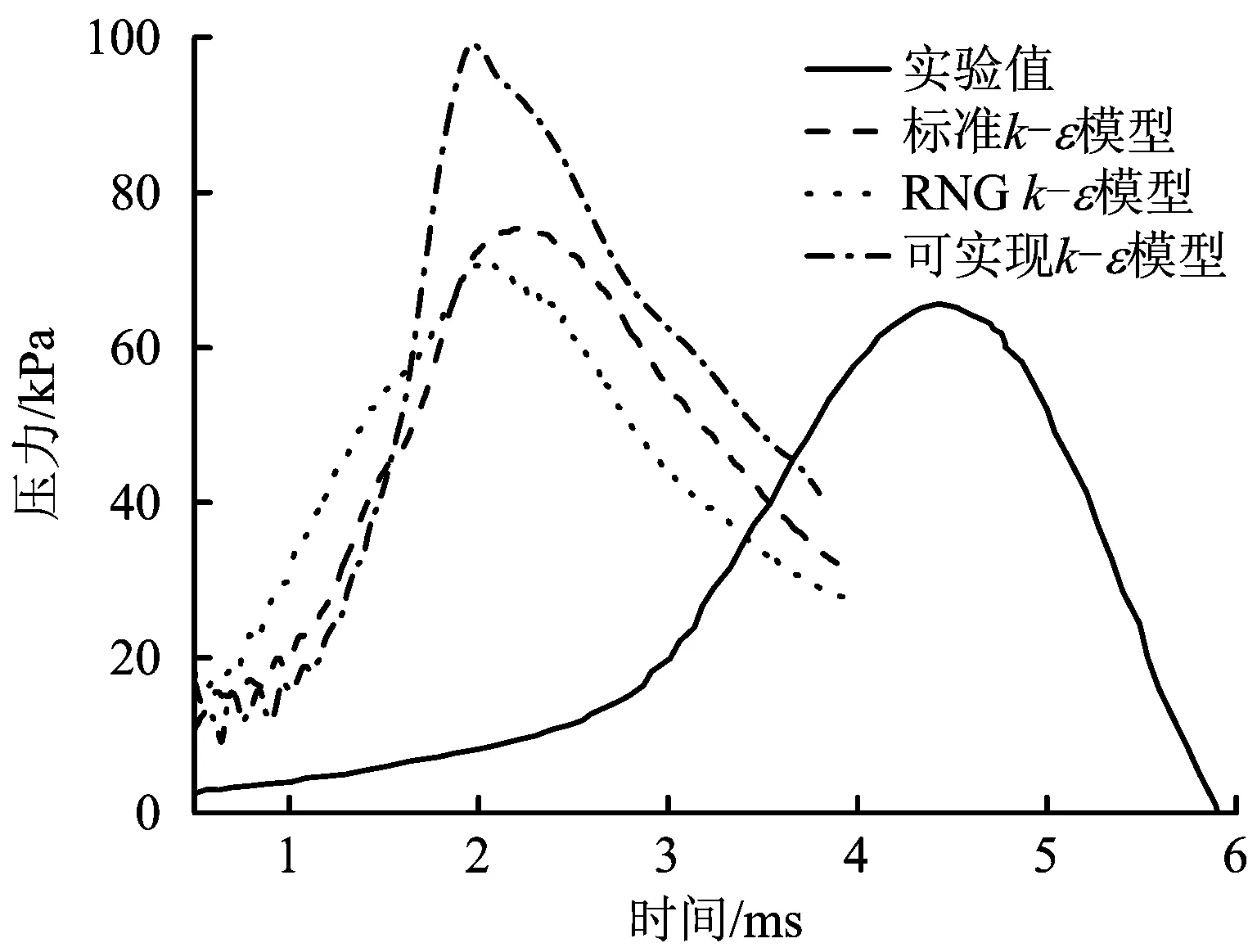
图6 不同k-ε湍流模型对应的燃烧压力变化Fig.6 Combustion pressure changes corresponding to different k-ε turbulent models

图7(a)为文献[4]给出的利用高速相机拍摄的在不同时刻下的火焰图片，氢气被点燃后形成半球形火焰，当火焰逐渐靠近障碍物时火焰锋面开始变得扁平，随后火焰从障碍物与管壁之间的空隙越过障碍物，翻越障碍物后两侧火焰锋面开始向管中心轴卷曲，直至相互融合。图7(b)～(d)为采用不同湍流模型进行数值模拟获得的火焰行为。由图7可知，与压力变化趋势相对应，利用数值模拟获得的火焰行为比实验结果提前2 ms左右。与实验拍摄到的火焰图像进行对比，发现如果采用可实现k-ε模型，当火焰通过障碍物与管壁之间的空隙时，火焰面很不清晰，且障碍物前的火焰区面积太小，与实验结果差别较大；与可实现k-ε模型相比，采用标准k-ε模型计算得到火焰从障碍物两侧通过以后，火焰面向管中心传播过程缓慢，在2 ms时，障碍物两侧火焰面的距离仍然比较大；RNGk-ε模型对应的火焰传播行为与实验结果吻合最好，更准确地反映了火焰受障碍物作用产生的变形和加速过程。

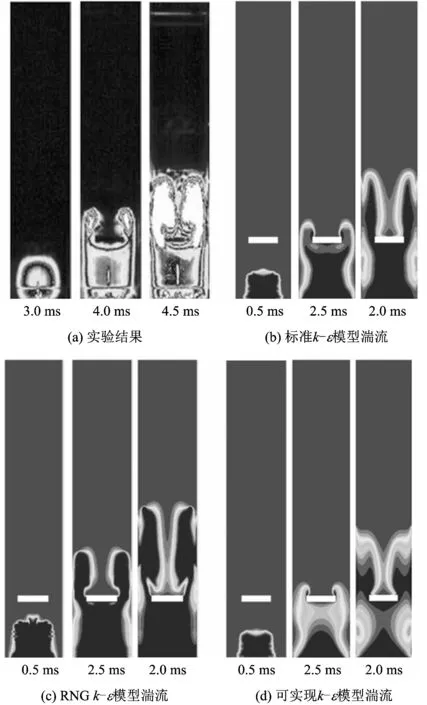
图7 不同湍流模型下的火焰行为与实验结果比较Fig.7 Comparison between the experimental results and the flame behaviors with different turbulence models

3.2 壁面函数对数值模拟的影响

根据湍流模型对数值模拟的影响分析结果，在分析壁面函数对数值模拟的影响时，湍流模型采用RNGk-ε模型。图8为采用不同壁面函数进行数值模拟所获得的燃烧压力与时间的关系，可以看出，标准和可伸缩壁面函数对应的结果很接近，如果采用非平衡壁面函数，在压力上升阶段压力值稍微变大。可伸缩、标准和非平衡3种壁面函数对应的压力峰值逐渐增加，与实验值相比较，压力峰值相对偏差分别为1.7%，7.9%和13.4%，可伸缩壁面函数的压力峰值与实验值最接近。图9为不同的壁面函数下的火焰行为与实验结果对比，对于火焰传播过程，如果采用非平衡壁面函数，火焰翻越障碍物后的传播速度比标准和可伸缩壁面函数的更快，使火焰形状显得更加细长。标准和可伸缩壁面函数对应的火焰行为基本一致，也与实验拍摄到的火焰行为较为吻合。

图8 不同壁面函数对应的燃烧压力变化Fig.8 Combustion pressure changes corresponding to different wall function

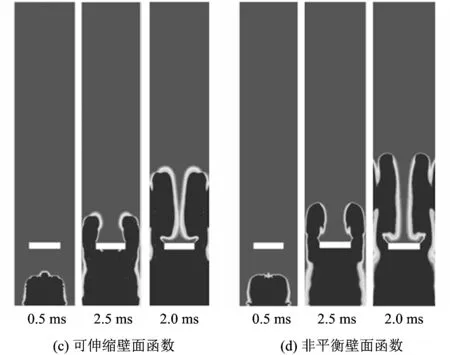
图9 不同的壁面函数下的火焰行为与实验结果对比Fig.9 Comparison between the experimental results and the flame behaviors with different wall functions

4 结论

1) 标准k-ε模型基本可以比较准确地预测出火焰燃烧压力变化和火焰传播行为。RNGk-ε模型考虑了湍流旋涡，数值模拟结果更准确。可实现k-ε模型使燃烧压力值和火焰形状与实际情况相比偏差较大。

2)利用标准壁面函数和可伸缩壁面函数预测出的火焰行为与实验结果都很吻合，但非平衡壁面函数对被障碍物扰动的火焰有比较明显的加速，使火焰形状与实际情况不符。从燃烧压力上看，可伸缩壁面函数的压力峰值与实验值最接近，非平衡壁面函数的压力峰值与实验值相比偏差最大。