减振器阀片尺寸对阻尼力影响仿真及试验研究

周安江，杨礼康，杜嘉鑫，徐云奎

(1.浙江科技学院 机械与能源工程学院，杭州 310023；2.浙江华昌液压机械有限公司，杭州 310021)

伴随着中国经济的平稳快速增长，铁路行业在中国也得到了迅猛发展。2017年国家发展改革委、交通运输部、国家铁路局、中国铁路总公司印发《铁路“十三五”发展规划》，规划提出，到2020年，全国铁路营业里程达到15万公里，其中高速铁路3万公里[1]。在此背景下，轨道车辆的研究与发展显得尤为重要。在轨道车辆的研究中，对行驶平顺性和操纵稳定性有着直接影响的轨道车辆减振器始终是研究的重点，减振器性能的好坏直接影响到乘坐舒适性和安全性[2-5]。轨道车辆减振器内部节流阀片中的复原阀片、压缩阀片与活塞结构尺寸之间的合理设计，对减振器阻尼力输出性能有着直接影响[6]。周长城等针对不同当量厚度和相同当量厚度的叠加阀片对减振器阻尼特性的影响进行了试验[7]，但缺少对不同直径节流阀片对减振器阻尼特性影响的研究。杨成龙等对减振器复原阀和压缩阀的不等外径多阀片结构弯曲变形进行了分析，求得了不等外径多阀片结构变形解析理论公式并通过ANSYS仿真结果进行了对比[8]，但缺乏试验验证。因此，笔者针对以上问题开展了轨道车辆减振器节流阀片对其性能影响的试验研究及仿真分析。

1 轨道车辆减振器阻尼特性

1.1 轨道车辆液压减振器活塞结构与工作原理

图1 活塞总成 Fig.1 Piston assembly 1—压紧螺母；2—复原垫片； 3—活塞部件；4—复原阀片； 5—活塞；6—压缩阀片； 7—压缩垫片；8—凸台。

某型轨道车辆液压减振器主要部件有活塞缸单元和储油缸单元两部分。活塞缸内有配备活塞杆和活塞总成，活塞杆上部有防尘盖、活塞杆导向套、O形圈和往复油封。活塞缸下端有底阀总成。活塞上部为压缩阀，下部为复原阀，包含压缩阀片和复原阀片、压缩垫片及复原垫片、压紧螺母、凸台、活塞和活塞部件等，如图1所示。储油缸内上部是空气，下部减振器油液通过底阀与活塞缸连通，当减振器活塞杆往复运动或因温度变化使油液体积变化时，储油缸对活塞缸油液进行接收或补偿。当油液流经节流阀系时，发生节流作用，产生阻尼力，从而减弱车身与轨道间的相对运动，起到减振作用[9-11]。

1.2 活塞节流阀片工作特性

阀片是影响减振器阻尼特性的关键零件[12-13]，其中，阀片厚度与常通节流孔面积是减振器阻尼特性的重要影响因素[14]。实际结构中，液压减振器节流通常采用多片阀片叠加的形式[15]。

当减振器处于复原行程时，工作缸上腔的油液经过复原阀流入下腔，同时储油筒内的部分油液通过补偿阀进入工作缸下腔，此时通过复原阀和补偿阀产生复原节流压力。当减振器运行速度高于复原阀开阀开启速度时，复原阀开阀，油液通过常通节流孔及复原阀片变形所形成的节流缝隙产生节流压力。当减振器运行速度低于复原阀开启速度时，复原阀闭合，只产生油液经过常通节流孔的节流压力。

当减振器处于压缩行程时，活塞缸筒下腔中的部分油液经过流通阀流入缸筒上腔，余下部分油液则经过底阀流入储油缸筒内，油液通过压缩阀和流通阀产生压缩节流压力。当减振器运行速度大于压缩阀开阀速度时，压缩阀开启，油液通过常通节流孔及压缩阀片变形所形成的节流缝隙产生节流压力。当减振器运行速度低于压缩阀开启速度时，压缩阀不开启，只产生油液经过常通节流孔的节流压力[16]。

2 数学模型

2.1 复原行程

复原行程中，设底阀阀系流量为Q1，流经活塞的流量为Q2。试验用底阀及活塞常通孔的长径比均小于0.5，属于薄壁小孔，所以底阀及活塞阀系的常通节流孔压差[16]111：

(1)

式(1)中：A1,2为底阀及活塞阀系常通孔有效面积；N1,2为常通孔数量；Q11,21为流经底阀常通孔和活塞常通孔的流量。

A1,2=l1,2h1,2。

(2)

式(2)中：l1,2为底阀及活塞阀系常通孔宽度；h1,2为底阀及活塞阀系常通孔高度。

底阀及活塞阀系节流缝隙压差：

(3)

式(3)中：rbf为节流阀片外半径；rkf为节流阀片阀口位置半径；Q12,22为流经底阀缝隙和活塞缝隙的流量。

试验用活塞孔的长径比为2.4，属于短孔，所以活塞孔压差：

(4)

式(4)中：Q23为流经活塞孔的流量；A23为活塞孔面积；N23为活塞孔个数。

复原行程中，活塞阀片和底阀阀片开阀前，油液仅经流常通孔，此时Q1=Q11，Q2=Q21。当减振器运行速度达到活塞阀片开阀点，即此速度下经活塞部分流向工作缸下腔时，油压克服活塞复原阀片的弹性力，将复原阀片推开形成弯曲，使活塞阀片和底阀阀片开阀产生圆环盘缝隙，工作缸内油液通过活塞常通孔、活塞孔及活塞开阀节流阀片缝隙流通，储油缸内油液经由底阀常通孔和底阀开阀节流阀片流通。活塞端常通孔与活塞孔及活塞复原阀系，底阀端常通孔与复原阀系，均为并联关系，此时Q1=Q11=Q12，Q2=Q21+Q22，Q22=Q23。

底阀阀系开阀前后总压差分别为：p1=p11,p1=p11+p12。

活塞阀系开阀前后总压差分别为：p2=p21,p2=p21+p22+p23。

则复原阻尼力：

F1=p2(Ah-Ag)+p1Ah。

(5)

式(5)中：Ah为活塞端面积；Ag为活塞杆面积。

2.2 压缩行程

在压缩行程中，设底阀阀系流量为Q3，流经活塞的流量为Q4。底阀及活塞阀系的常通节流孔压差p31和p41由式(1)～(2)得出。

底阀及活塞阀系节流缝隙压差：

(6)

式(6)中：f为节流阀片变形量，μ为动力黏度。

压缩行程活塞孔两侧压差：

(7)

式(7)中：Q43为压缩行程中流经活塞孔的流量；A43为活塞孔面积；N43为活塞孔个数。

压缩行程中活塞端及底阀端压缩阀系节流阀片开阀前压差为：p3=p31，p4=p41。

当减振器运行速度达到压缩阀片开阀点，即此速度下油液经活塞部分流向工作缸上腔时，油压克服活塞压缩阀片的弹性力，将压缩阀片推开形成弯曲，使压缩阀片和底阀阀片开阀产生圆环盘缝隙，此时压缩行程中活塞端及底阀端压缩阀系节流阀片开阀后压差：p3=p31+p32。

活塞阀系总压差：p4=p41+p42+p43。

压缩行程减振器阻尼力：F2=p4(Ah-Ag)-p3Ah。

2.3 阀片弯曲变形

根据弹性力学原理，得到圆形薄板弹性阀片弯曲变形面微分方程[17]：

(8)

(9)

式(8)～(9)中：D为常数；E为阀片弹性模量；ε为阀片泊松比；r为阀片半径；δ为阀片等效厚度；q为载荷。

式(8)的通解：

f=C1lnr+C2r2lnr+C3r2+C4+f*，

(10)

(11)

式(10)中：C1～C4为任意常数，取决于边界条件。

该弹性阀片内圆为固定约束，外圆为自由约束，内圆外圆边界条件分别为：

(12)

M|r=rb=0；Q|r=rb=0。

(13)

式(12)中：ra为阀片内圆有效半径。式(13)中：rb为阀片外圆有效半径。

根据边界条件可以得到:

(14)

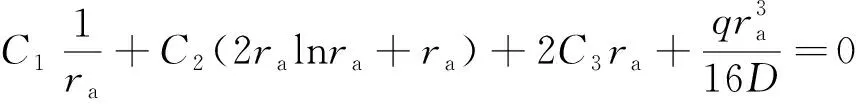
(15)

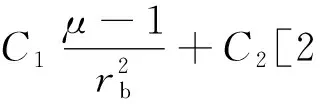
(16)

(17)

根据式(14)～(17)，可以求得C1～C4，再将其代入式(10)即可求得阀片在半径r处的变形量。

2.4 阀片叠加

液压减振器节流阀片通常采用多片阀片相互叠加的形式，通过不同的叠加组合以满足减振器不同阻尼特性的要求。采用多片节流阀片叠加的形式时，为了保证减振器阻尼特性设计值与实际值一致，则必须保证在相同载荷下，减振器叠加节流阀片等效厚度he与设计厚度相同。根据节流阀片受力情况，节流阀片相互叠加时，各阀片受力不相等，但所受力之和等于总载荷，即：

p=p1+p2+…+pn。

根据节流阀片变形情况，节流阀片叠加时各阀片变形量相等，等于总变形量，即：

(18)

式(18)中：Gr为节流阀片位置半径r处的阀片变形系数，也叫“长城系数”[15]。

2.5 MATLAB/Simulink仿真

对减振器的复原和压缩行程进行分析后，在MATLAB/Simulink中分别对减振器复原、压缩行程及其开阀前后进行仿真。Smulink仿真模型如图2。其中，减振器运行频率以及振幅大小通过Sine Wave模块进行调节，该模块输出值为减振器位移，通过将Sine Wave模块连接Derivative模块来对减振器位移进行求一阶导数，得到减振器运行速度。然后减振器复原行程、压缩行程通过Saturation模块对减振器运行速度进行正负值限定加以区分，活塞节流阀片开阀与否以及底阀节流阀片开阀与否，同样也是通过Saturation模块设定开阀速度点来对活塞节流阀片以及压缩节流阀片开阀与否来进行区分。底阀常通孔模型与活塞常通孔模型建立方法相同。

图2 减振器Simulink模型Fig.2 Simulink model of shock absorber

3 减振器性能试验及对比

3.1 试验设备及试验方案

试验设备包括PC端及控制软件、电液伺服控制器、某型液压减振器以及减振器试验台。为分析节流阀片直径对减振器阻尼力的精确影响，采用不同直径节流阀片进行试验，使用的活塞部分节流阀片直径为37.5、38.5、43、44.5 mm 4种。为分析底阀部分节流阀片厚度对减振器阻尼力的影响，利用不同叠加片数的直径15 mm的节流阀片进行试验。

3.2 压缩阀片阻尼性能对比及模型仿真

选取直径为43 mm与44.5 mm的压缩阀片进行对比，试验结果如图3～4所示，其中低速段显示为压缩阀片开阀前力-位移曲线，高速段为压缩阀片开阀后力-位移曲线。

图3 直径43 mm压缩阀片力-位移图Fig.3 43 mm compression disc force-displacement

图4 直径44.5 mm压缩阀片力-位移图Fig.4 44.5 mm compression disc force-displacement

图5 压缩阀片开阀后力-位移仿真图Fig.5 Compression disc front force-simulation

针对不同直径及压缩阀片开阀前后4种情况，运用Simulink进行仿真。因为低速段节流阀片未开阀，减振器油液只通过活塞及底阀常通孔进行流通，所以节流阀片直径变化对减振器低速段的阻尼性能影响有限，故只针对高速段节流阀片完全开阀的情况进行仿真。其中，43 mm直径压缩阀片和44.5 mm压缩阀片开阀后的示功图如图5所示。

由图5可知，在压缩行程高速开阀段，直径43 mm压缩阀片阻尼力为5 462 N，仿真结果为5 387 N，相对误差1.3%；直径44.5 mm压缩阀片阻尼力为5 926 N，仿真结果为5 886 N，相对误差0.6%。

3.3 复原阀片阻尼性能对比及模型仿真

选取直径为37.5 mm与38.5 mm的复原阀片进行对比，试验结果如图6～7所示，其中低速段显示为复原阀片开阀前力-位移曲线，高速段为复原阀片开阀后力-位移曲线。

图6 直径37.5 mm复原阀片力-位移图Fig.6 37.5 mm rebound disc force-displacement

图7 直径38.5 mm复原阀片力-位移图Fig.7 38.5 mm rebound disc force-displacement

由图8可知，在复原行程高速开阀段，直径37.5 mm复原阀片阻尼力为5 836 N，仿真结果为5 747 N，相对误差1.5%；直径38.5 mm复原阀片阻尼力为6 448 N，仿真结果为6 472 N，相对误差-0.3%。

3.4 底阀节流阀片阻尼性能对比及模型仿真

底阀部分采用直径15 mm，厚度0.3 mm节流阀片，叠加形式为3片叠加和4片叠加，试验结果如图9～10所示。节流阀片未开阀时阻尼力表现如图中低速段显示，当节流阀片开阀时，阻尼力表现如图中高速段所示。

图9 3片节流阀片叠加力-位移图Fig.9 Superposition force of three discs-displacement

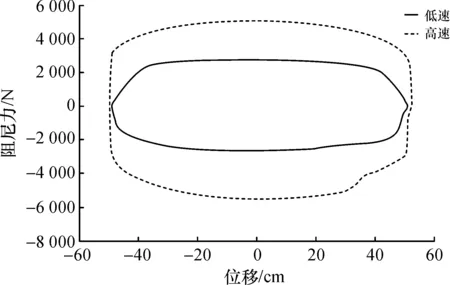
图10 4片节流阀片叠加力-位移图Fig.10 Superposition force of four discs-displacement

针对两种叠加厚度节流阀片组，根据叠加节流阀片等效厚度理论，模型中相应的等效厚度分别为0.433 mm和0.476 mm。减振器低速运行，节流阀片开阀前阻尼力仿真结果如图11。减振器高速运行，节流阀片开阀后阻尼力仿真结果如图12。

图11 叠加节流阀片开阀前力-位移图Fig.11 Superimposed throttle discfront force-displacement

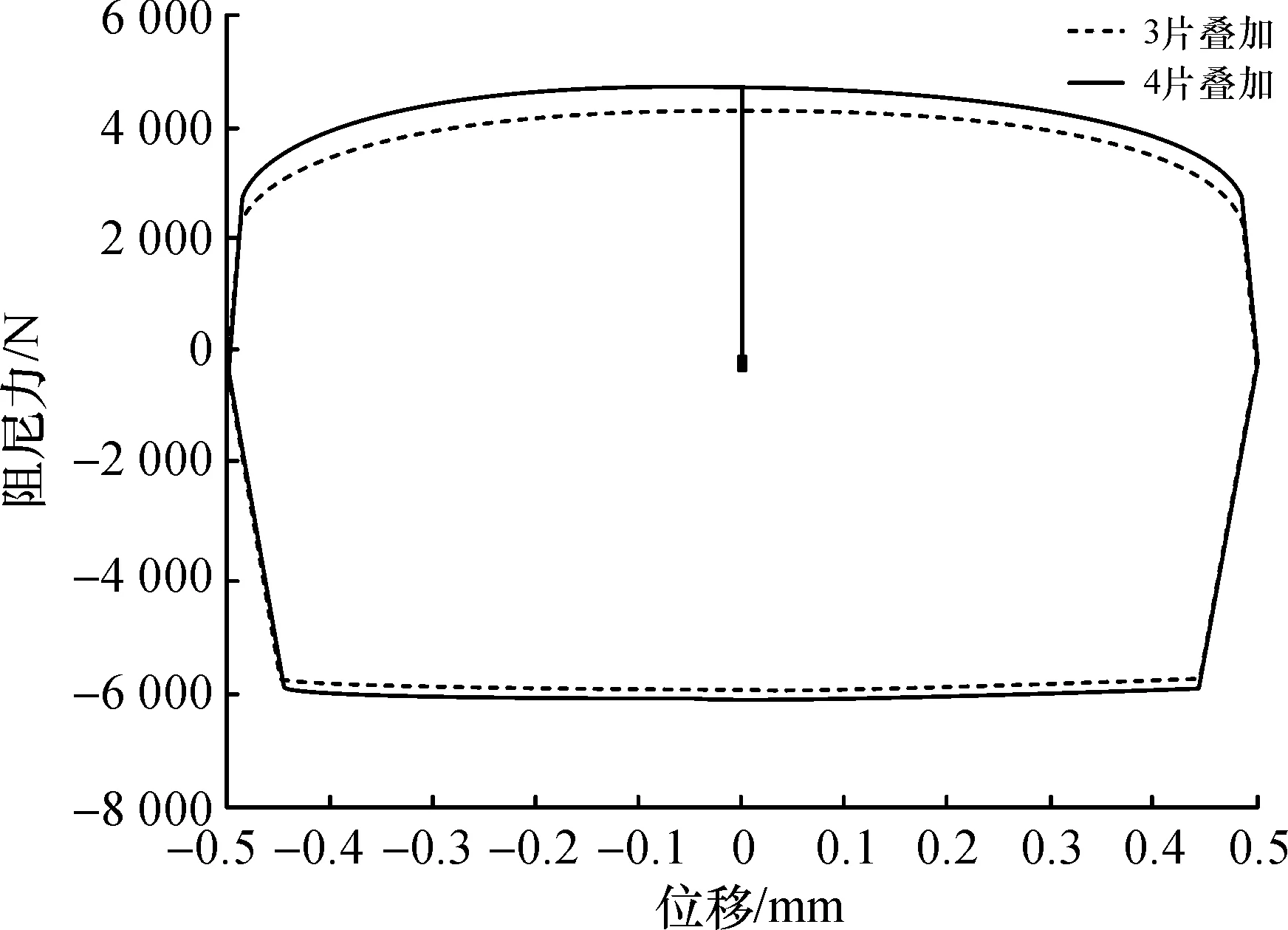
图12 叠加节流阀片开阀后力-位移图Fig.12 Superimposed throttle disc rearforce-displacement

由表3可知，底阀叠加节流阀片增加1片时，减振器低速和高速复原力变化较为明显，试验得到复原阻尼力低速差值为1 016 N，而高速差值为997 N。同时，由表4可知，底阀叠加节流阀片对压缩阻尼力的影响较小，试验得到压缩阻尼力低速差值为228 N，而高速差值为77 N。阻尼力仿真数值在复原行程低速段及压缩行程高速段符合较好。

表3 底阀叠加节流阀片复原阻尼力表现Table 3 Rebound damping force performance of bottom valve superimposed throttle discs

表4 底阀叠加节流阀片压缩阻尼力表现Table 4 Compression damping force performance of bottom valve superimposed throttle discs

4 结 论

本文对采用“均布载荷作用的环形薄板挠曲变形”理论的减振器数学模型进行了 MATLAB/Simulink仿真，仿真结果和试验结果基本上一致，具体结论如下：

1)对于不同直径节流阀片，阀片直径增加，减振器在节流阀片开阀后的阻尼力也会增加。

2)对于相同规格叠加节流阀片，叠加的片数越多，等效厚度越大，相应的阻尼力也会随之增加。

该试验结果及仿真模型在阀片规格变化时减振器阻尼力变化情况的试验结果，可为减振器的设计开发提供参考。