带违约风险分数维随机利率欧式看涨期权定价

王 伟，胡俊娟

(浙江科技学院 理学院，杭州 310023)

20世纪70年代，Black等[1]和Merton[2]的两篇开创性论文，突破性地给出了期权定价的Black-Scholes-Merton公式(以下简称BS公式)，作为期权定价研究的里程碑，该公式自问世以来就得到了学术界的一致好评。在假定股票的价格服从几何布朗运动，无市场交易成本，且股票价格的波动率σ、红利率q和无风险利率r均为常数的前提下，他们应用无套利原理给出了期权定价公式。但是，实证研究的结果表明，股票价格在绝大多数情形下并不符合几何布朗运动的特征，而是与几何分数维布朗运动的特性相符合。因此，很多研究者提出用分数维布朗运动来替代布朗运动的观点。Elliot等[3]研究了分数白噪声的一般理论及其在金融中的应用；Biagini等[4]系统介绍了分数维布朗运动的随机积分的一系列结果及其应用。另外，国内一些研究者也相继展开了基于分数维布朗运动这一假定的金融衍生品定价的研究，如文献[5-8]。在以上研究中，无论是BS公式，还是分数维BS公式，在基本假定上都有一个共同点，即在期权有效期内利率r是常数。然而利率的不确定性也成为实证研究中的一个越来越明显的特征，因此国内外研究者做了关于利率非常数情形下期权定价的广泛探讨，例如，假定在期权有效期内利率r是时间的确定性函数，推导并给出了相应的BS公式。但是，利率r是随机变量似乎更加贴近现实。对此，国外早期的研究，如：Merton[2]假设不支付红利，公司价值遵循几何布朗运动，利率随机，推导出了零息票债券的定价公式；Baxter等[9]在等价鞅测度下研究了利率波动的金融资产的定价公式；Kung等[10]假定短期利率服从Merton模型，股票价格模型仍然由几何布朗运动驱动，研究了欧式期权定价。近些年来，国内也有对此开展研究的，如文献[11-13]，但目前国内基于这一条件下的研究成果尚显不足。另外，违约风险已成为当今世界金融市场所面临的重大挑战。美国次贷危机以来，国内外屡屡出现公司破产现象，特别是2008年美国第四大投行雷曼兄弟递交了破产保护申请，人们才终于醒悟并认识到没有绝对安全的金融产品，从而大部分的金融衍生品都被戴上了“违约风险”的帽子。事实上，在期权定价中考虑违约风险的影响这一研究早就展开了，文献[14-16]在期权定价时考虑违约风险，并将该种期权称为脆弱期权，推导出脆弱期权的定价公式，并运用数值方法将脆弱欧式期权、美式期权与标准期权的定价进行对比，特别地，假设公司的信用风险与其基础资产价值相关，得到了脆弱期权的定价公式。就中国金融市场而言，如何防范信用风险是目前金融界面临的重大问题之一。国内也有研究在期权定价中考虑了违约风险的影响，并得到了一些结论，如文献[17-19]，但该研究仍然存在着很大的探索空间。因此，在分数维布朗运动环境中开展对期权定价的研究，同时考虑利率的随机性对定价的影响，已逐渐成为研究的热点。另外，对带有违约风险的期权定价的研究有助于为中国金融业管理和控制信用风险提供理论上的指导。针对分数维Ho-Lee利率模型下的具有违约风险的欧式看涨期权定价公式，笔者在文献[17]中对其简化模型进行推导证明，在本文中，则进一步对更为一般的Vasicek模型进行研究。

1 基本模型

1.1 分数布朗运动环境中的常数利率的公司资产价值模型

Xd(T)=X(T)IV(T)>D+δ(T)X(T)IV(T)≤D。

(1)

式(1)中：欧式看涨期权的损益为X(T)=maxS(T)-K,0，其中T为到期日，S(T)为T时刻的标的资产价格，K为欧式看涨期权的执行价格；IA为集合A的示性函数。

假设公司资产价值V(t)和标的资产价格S(t)在等价鞅测度下分别满足如下随机微分方程：

(2)

(3)

式(2)～(3)中：μs,μv,σsj>0,σvj>0均为常数；WHj(t),0≤t≤T(j=1,2,…,m)是参数为Hj(j=1,2,…,m)的定义在完备概率空间上的分数布朗运动，且它们是相互独立的。

引理1[4]式(2)～(3)的解分别为

假定无风险资产价格B(t)满足

dB(t)=rB(t)dt，B(0)=1，0≤t≤T，

则B(t)=exprt，其中r为常数。

定义1[17]标的资产价格S(t),t≥0在0,T上的期望回报率β(t)定义为

引理2[17]S(t),t≥0在0,T上的βs(t)和V(t),t≥0在0,T上的βv(t)分别满足如下：

βs(t)=μs，t∈0,T，

βv(t)=μv，t∈0,T。

显而易见，有ES(T)=μs，EV(T)=μv，t∈0,T。

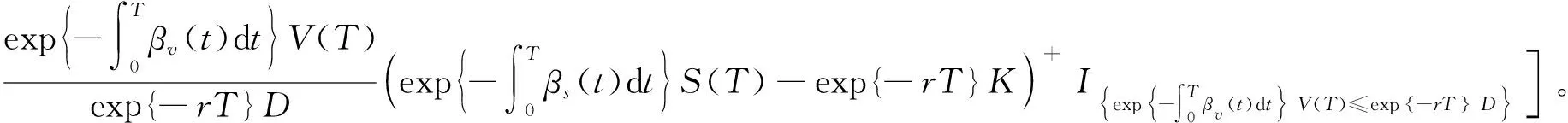
(4)

式(4)中：S(t)可由期望回报率βs(t)贴现；V(t)可由期望回报率βv(t)贴现；D可由无风险利率r贴现。

1.2 分数布朗运动环境中的随机利率模型

假设利率随机运动，在前面的等价鞅测度下，其运动满足如下随机微分方程：

dr(t)=h(t,r(t))dt+g(t,r(t))dω(t)。

(5)

式(5)中：h(t,x),g(t,x)均为时间的函数，赋予其不同的假设会导致不同的利率模型，如Ho-Lee、Vasicek、Cox-Ingersoll-Ross(CIR)、Hull-White等。本研究仅假定利率服从Vasicek随机利率模型，并将其推广为分数维Vasicek随机利率模型，对欧式看涨期权的定价进行研究。

Vasicek模型的一般形式为

dr(t)=a(b-r(t))dt+σrdω(t)。

(6)

式(6)中：a,b和σr均为非负的常数。将其推广为分数布朗运动下的随机利率，即满足拟鞅测度Q下的随机微分方程

dr(t)=a(b-r(t))dt+σrdωH(t)。

积分变换后可得一Ornstein-Uhlenbeck过程：

由文献[11]的定理2.1知，r(t)仍旧服从正态分布，且有

(7)

1.3 带违约风险的分数随机利率下的公司资产价值模型

假定无风险资产价格B(t)满足

dB(t)=r(t)B(t)dt，B(0)=1，0≤t≤T。

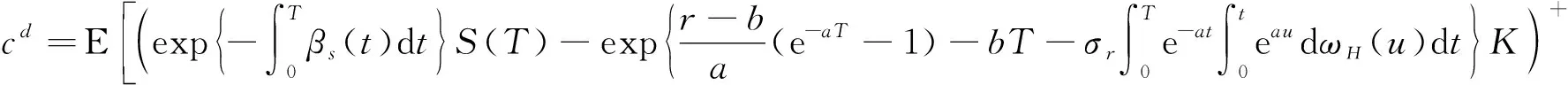
(8)

式(8)中：S(t)可由期望回报率βs(t)贴现；V(t)可由期望回报率βv(t)贴现；D可由分数维Vasicek随机利率r(t)贴现。

2 带违约风险的欧式看涨期权定价

借助BS模型的基本假设条件，给出了以下假设：1)公司资产价值和标的资产价格服从分数布朗运动；2)利率遵循分数维Vasicek随机利率模型；3)无税收、无摩擦；4)不支付红利q；5)无套利机会。

令

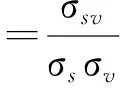
从而-Zs,-Zv服从参数为ρ的二维正态分布，其密度函数为

再令

对A1中不等式两边取对数，再由定义1，有

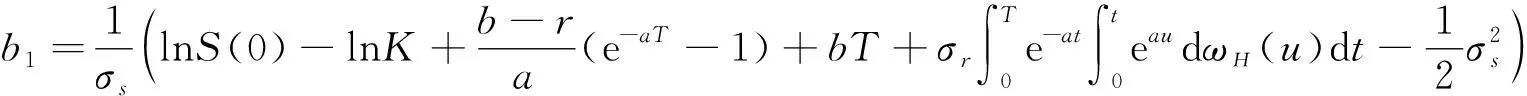
A1=b1>-Zs。

(9)

同理可得

A2=b2>-Zv。

(10)

式(10)中，

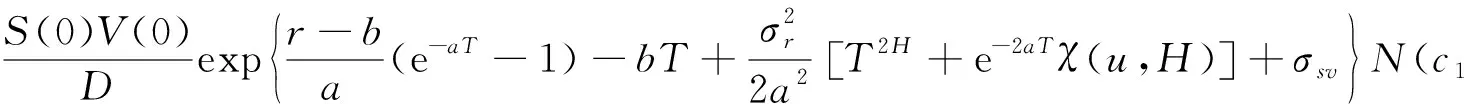
(11)

证明：

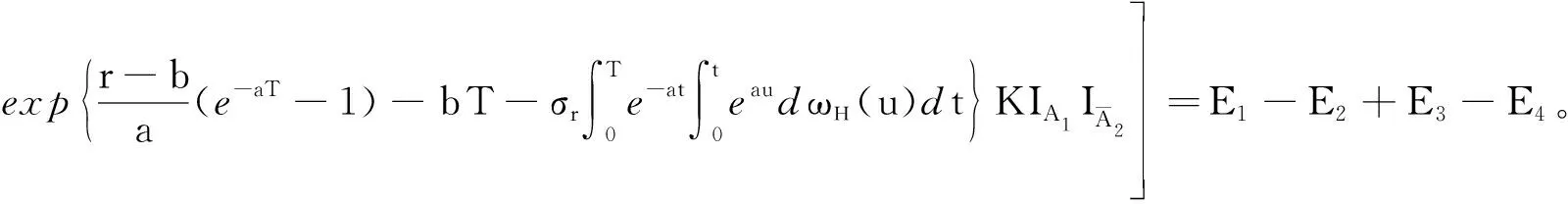
(12)

式(12)中，

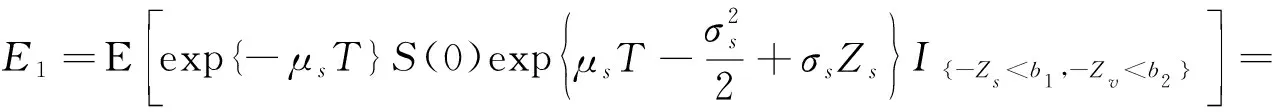
(13)

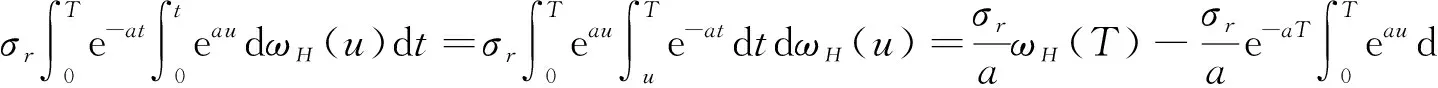
则

(14)

从而

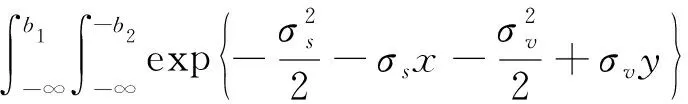
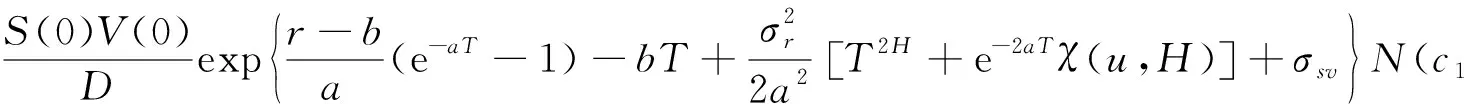
3 结 论

本研究在分数维布朗运动环境中，综合考虑了违约风险和利率随机性对欧式看涨期权定价的影响，从而更接近现实。采用了分数布朗运动随机微分方程理论及期权定价的保险精算方法，考虑了违约风险的影响，选取了Vasicek随机利率模型，并将之与分数布朗运动相结合，拓展了其内涵，推导出了欧式看涨期权定价公式的解析式。下一步，还可同时考虑波动率为随机的情形来进行更深入的探讨。