基于BDS的数字轨道辅助列车定位方法研究
王鹏飞,李卫东,初宪武,王新屏
(1.大连交通大学 电气信息学院,辽宁 大连 1160282; 2.河南工学院 机械工程系,河南 新乡 453003)*
0 引言
铁路运输具有不同于公路运输的特点,其运输的货物多样,适合运输重载货物,其中部分高附加值货物关系到国家政治、军事以及企业、百姓等广泛利益.提高铁路系统运输安全和能力,有效管理铁路高附加值货物运输成为我国经济和社会发展中日趋紧迫的任务.欧美国家一直在用卫星定位跟踪技术为重要货物运输提供有力保障,并在高附加值货物押运上形成了一系列专用的工具,如安全运载箱、押运车辆定位终端等.
利用国外卫星导航系统资源对我国许多领域具有很大的风险性,不能满足我国对信息、交通安全的要求.经过多年发展,北斗卫星导航系统(BDS)已经能够为我国军用和民用领域以及经济和社会发展的各领域提供自主安全、高质量的卫星通信服务.
现有水平的铁路物流跟踪手段是通过对列车的定位跟踪来实现的.常用的定位方法一般是利用轨边设备进行定位[1].应答查询定位是一种常见的列车定位方法,可实现高精度定位,但是需沿途铺设定位设备,且只能进行定点跟踪定位.测速定位通过测量运行速度并根据时间推算距离,从而计算出列车位置,但此方法存在定位误差积分的影响.因此,现在使用的定位跟踪方法不仅无法实现对列车实时、高精度跟踪定位,更重要的是缺乏对具体货物的实时跟踪定位.
BDS作为一种全球卫星导航系统可以全天候、连续对列车定位,具有实时定位精度高、成本低、体积小、维护方便等优势.同时,准确的位置信息对列车安全可靠地运行也至关重要,铁路货运及调度需要更为优化的列车定位技术[2].因此,对基于BDS的列车定位方法进行深入研究,对于推动铁路运输业的发展具有重要意义.
1 列车定位问题描述
基于列车位置的空间从属性,数字轨道线路为地理坐标与一维轨道坐标体系的映射提供了有效途径.根据线路图信息在定位处理逻辑中的耦合深度不同,可以将其划分为不同层次,其中松耦合模式由于对设备性能要求不高,实现方法相对方便,所以更适用于列车经济性定位.目前,地图辅助定位已形成了基于线路拓扑分析、相似度、概率描述等多种不同类别的计算方法[3].
基于BDS进行货运列车定位时,可以首先计算列车(定位天线)到卫星的伪距,进而可以得到其他的列车运行状态参量,包括位置、速度等[4].式(1)即为对列车运行状态的描述.
xi=f(xi-1)+wi+ci
(1)
式中,xi为列车运行状态向量;f(*)为系统方程;wi为系统噪声;ci为修正向量.
列车定位可以根据需求选择不同的定位方法,如采用卫星导航系统单独定位或者采用惯性、航位推算系统与卫星导航系统组合定位[5].无论哪种方法,测量向量最终都需要利用地图匹配使其受约束至铁路轨道线路.本文以BDS的非差精密观测定位与数字轨道线路约束为研究对象.
BDS的非差精密定位观测方程为:
Φij(tr)=Φri(tr)-Φsj(tr)+N+εij(tr)
(2)
式中,tr为列车定位采样时刻;Φri(tr)为振荡相位;Φsj(tr)、N是卫星j的载波相位和整周模糊度;Φri(tr)是系统观测噪声.
2 数字轨道线路
常规轨道线路图由沿轨道测量的离散测点及相关信息组成.铁路轨道的测点根据精度可分为低精度(<10 m)和高精度(<1 m),低精度的测点可以生成近似轨道线路,线路图由单线构成.而高精度测点生成的轨道线路可以区分双线轨道及道岔.
轨道线路生成一般采用直线逐个连接离散点的方法近似轨道曲线.线路生成时需要由BDS的CGCS2000坐标系转换到地图中的笛卡尔坐标系.一般采用常用的高斯-克吕格投影方法进行坐标转换.坐标系转换公式为:
(3)
式中,x,y分别为高斯平面纵坐标与横坐标;X为子午线弧长;
为中央子午线经度.B和L分别为纬度和经度,a和b分别为地球椭球体的长短半轴.
2.1 轨道信息
铁路的轨道主要由三类线型构成,分别是直线、圆曲线以及缓和曲线,不同的线路其组合方式不同.其中缓和曲线用于连接直线与圆曲线.在我国,铁路一般采用三次曲线作为缓和曲线的首选线型[6].而且圆曲线和缓和曲线均为曲线.所以一般来说轨道线路是由直线、曲线组合而成[7].
铁路线路网络可以用由节点构成的拓扑结构和几何形状模型表示,其中线段的端点(节点)由纬度、经度定义,形状由节点限定[8].节点设置在线路的分支处或轨道末端.铁路片段用两个节点之间的线段表示,则线路图的精度取决于线路中节点的间距大小.
2.2 线路拟合方法
轨道线路的测点为低精度测点时,测点数据存在较大测量误差,轨道线路可采用曲线拟合的方法生成.考虑到铁路轨道线路的曲线段特点,选用三次样条曲线进行拟合.
为了保证曲线拟合效果,需要坐标X单调.铁路轨道线路总体是由始发站到终点站的曲线,一般可以通过坐标旋转保证X单调.坐标旋转矩阵方程为:
(4)
式中,θ为旋转角度;x0,y0为原坐标值.
2.3 线路插值方法
高精度数字轨道线路对列车的准确定位、轨道区分等具有重要的意义,其需要高精度的测点.高精度测点可以在卫星信号条件良好的情况下通过精密测量得到,其水平精度优于0.5 m(CEP).此时,轨道原始数据可视为真值点,在生成轨道线路时,线路曲线经过测点.
由于高精度数字轨道线路绘制时,测点数量相对较多,为减少运算量,而三次B样条曲线不需要X单调,所以不需要进行坐标旋转.本文采用反求控制点的非均匀三次B样条插值方法生成轨道线路,其中,反求曲线控制点是算法重点.
反求三次B样条曲线控制点的问题即:找到一组与型值点Qi(xi,yi)对应的特征多边形顶点Pi,使得三次B样条曲线Pi(t)以Qi(xi,yi)为节点.由于积累弦长参数法可以反映点集按弦长的分布情况.所以采用积累弦长参数法估算每个测点所对应的参数值t可以解决点集分布不均匀问题.三次B样条曲线需要C2级连续,可使用端点插值法反求曲线的控制点[9].设第i段曲线为:
(5)
式中,Pi,i=1,2,…,n+1为控制点;Ni,4(t)为三次B样条基函数.
由三次B样条曲线性质可得[7]:
Pi-1+4Pi+Pi+1=6Qi,i=1,2,…,n
(6)
方程组需要补充边界条件才能求解.利用端点切矢补充2个边界条件:
(7)
联立式(6)和式(7),利用追赶法可求得控制点.最后根据控制点和已知型值点,通过De Boor递推完成三次B样条插值.所得曲线随插值点间隔的缩小,逐渐接近实际曲线,具有良好的保形性和光滑性,理论上可满足高精度轨道线路需求.
3 轨道定位修正
铁路运行具有自身的特点,列车只能行驶在铁路轨道上.数字轨道线路辅助列车定位的基本思路是通过卫星导航系统追踪列车运行的轨迹与数字轨道线路图进行匹配,寻找列车当前的行驶位置,并将列车当前定位点修正到铁路线上.
3.1 直线段投射修正法
列车在直线段行驶时,可以通过投射法修正定位点的位置,提高定位精度.曲线段可以近似成由较短的直线段连接而成.当曲率半径为800 m时,测点间隔50 m时,近似误差为0.39 m,如图1所示.对于不同的曲率半径,依据不同的精度要求选取近似直线段的长度.
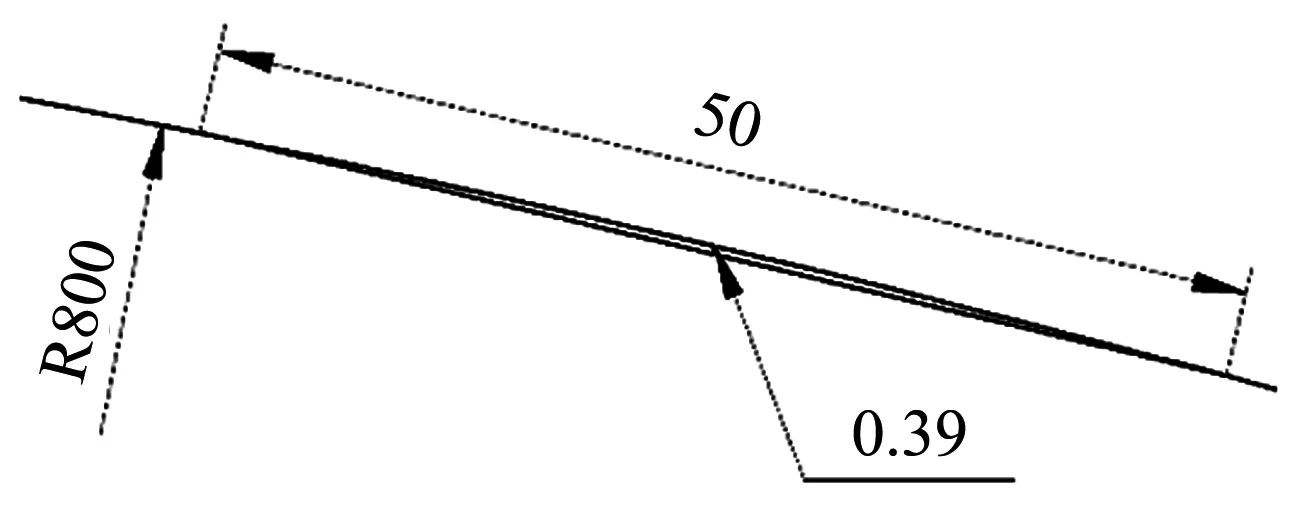
图1 近似误差图
当列车实际运行到P点时,此时列车位于直线AB之间,如图2所示,由于系统定位误差的存在,接收机计算获得的列车定位点为P0点,不在轨道直线上.根据定位点的误差圆,通过在线路表中搜索得到线段AB,卫星定位点P0到AB距离最小为P0P1,垂直于轨道航向AB,以P1点来评估列车的当前位置可适当减小定位误差.
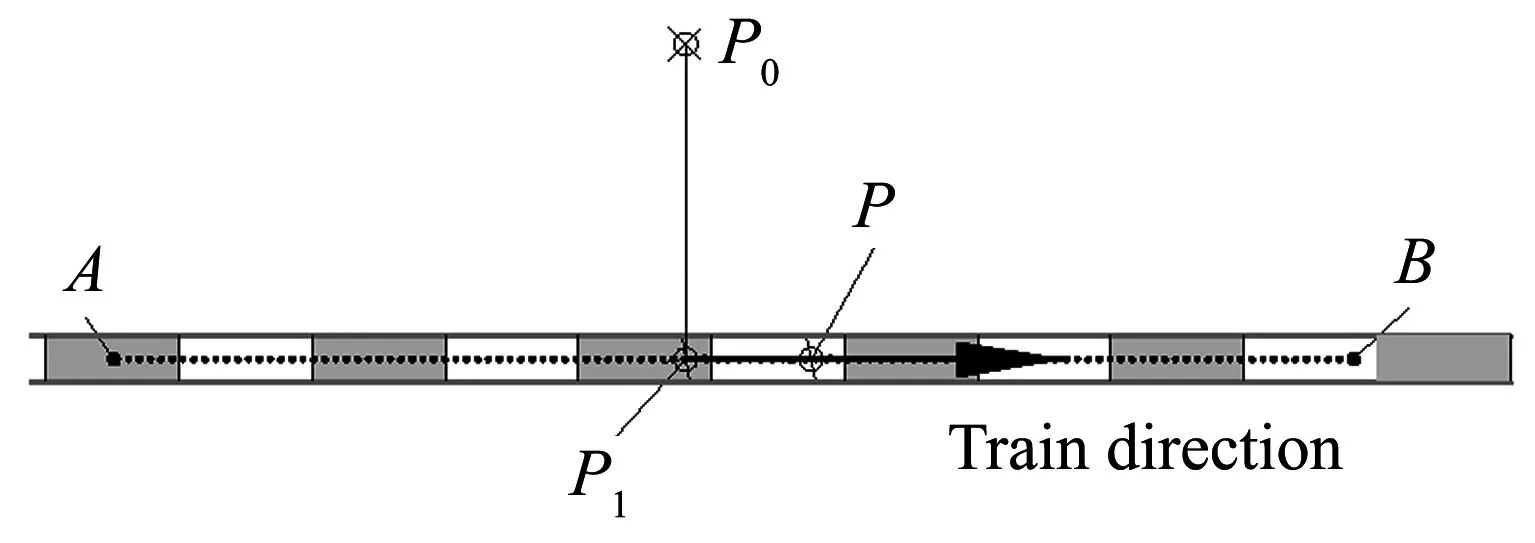
图2 卫星定位点修正示意图
3.2 多线并行轨道分辨法
轨道线路一般是多线并行情况,此时,纯几何的轨道线路分辨方法容易出错,可能出现列车在不同线路之间摇摆,所以需要采用不同的方法来判定此时的列车行驶轨道.
卫星定位点到轨道的距离越小,列车在该线路上行驶的可能性越大[10],如果距离小于一定的值,则可判定列车行驶在该线路上.为保证判定的有效性,设卫星定位点P0到线路T1的距离为D1,到线路T2的距离是D2,则当D1 通常铁路正线间距不小于4 m,所以如果要准确求出正确轨道线路,导航系统的定位误差须小于2 m,如图3所示. 图3 最短距离法 系统定位误差主要由卫星定位误差、线路修正残差、线路误差组成.卫星定位误差受周围环境状况的影响,也受大气层延迟、星钟误差、卫星轨道偏差和传播多径效应等多因素影响.线路自身的误差与测量点的精度及线路的生成方法有关. 本文以哈大线的某段货运铁路线为研究实例,实测数据点为非均匀点集,将点集P分为Pa,Pb两个子集,使用Pa子集进行拟合和插值运算,使用全集合P进行效果验证,从而仿真低、高两种不同精度的情况. 仿真时采用点集Pa进行三次样条拟合和三次B样条拟合,结果如图4所示. 图4(a)为线路总体拟合图,图4(b)为4(a)中圆圈部分的局部放大图.采用点集P进行拟合残差对比,如图5所示.通过图5可直观地发现三次样条曲线拟合残差较小. (a)总体拟合图 (b)局部图 图5 拟合残差对比 通过计算可得,三次样条拟合的SSE(残差平方和)为4.5×10-7,三次B样条拟合的SSE为2.7×10-6,所以三次样条用于线路拟合效果更好,更符合轨道线路实际情况. 图6为线路插值局部图.采用点集P进行插值效果对比,如图7所示,可直观发现三次B样条插值的误差更小. 通过对插值效果的分析与计算可得:三次样条插值方法的SSE为4.9×10-7,三次B样条插值方法的SSE为1.3×10-7,所以三次B样条插值效果优于三次样条插值. 图6 线路插值局部图 图7 插值效果验证 从图4~图7中可以看出,无论拟合还是插值,较大误差均出现在曲线段,而增加采样点集数量可以提高拟合和插值的精度.所以要保证轨道线路的自身精度需要适当增加曲线段的采样频率,从而提高线路的精度. 北斗卫星导航系统的安全性对于提高我国铁路系统运输安全和能力,以及有效管理铁路高附加值货物运输方面具有重要作用.本文根据测量数据精度的不同分别采用拟合和插值的方法构建数字轨道线路,然后采用投射修正法和多线并行轨道分辨法修正定位点,减小了定位误差.根据哈尔滨至长春货运铁路的部分轨道数据,分别建立了基于三次样条曲线、三次B样条曲线的拟合和插值模型.仿真结果表明,在低精度下,三次样条曲线拟合法优于三次B样条曲线拟合;在高精度下,基于反求控制点的三次B样条曲线插值更符合线路实际情况. 本文所用方法可以有效创建铁路轨道线路图,并修正列车定位位置,辅助北斗卫星导航系统提高列车的定位精度,对货运列车提高可靠性和安全性具有一定的实际意义.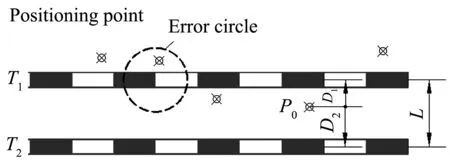
4 轨道线路仿真
4.1 拟合仿真
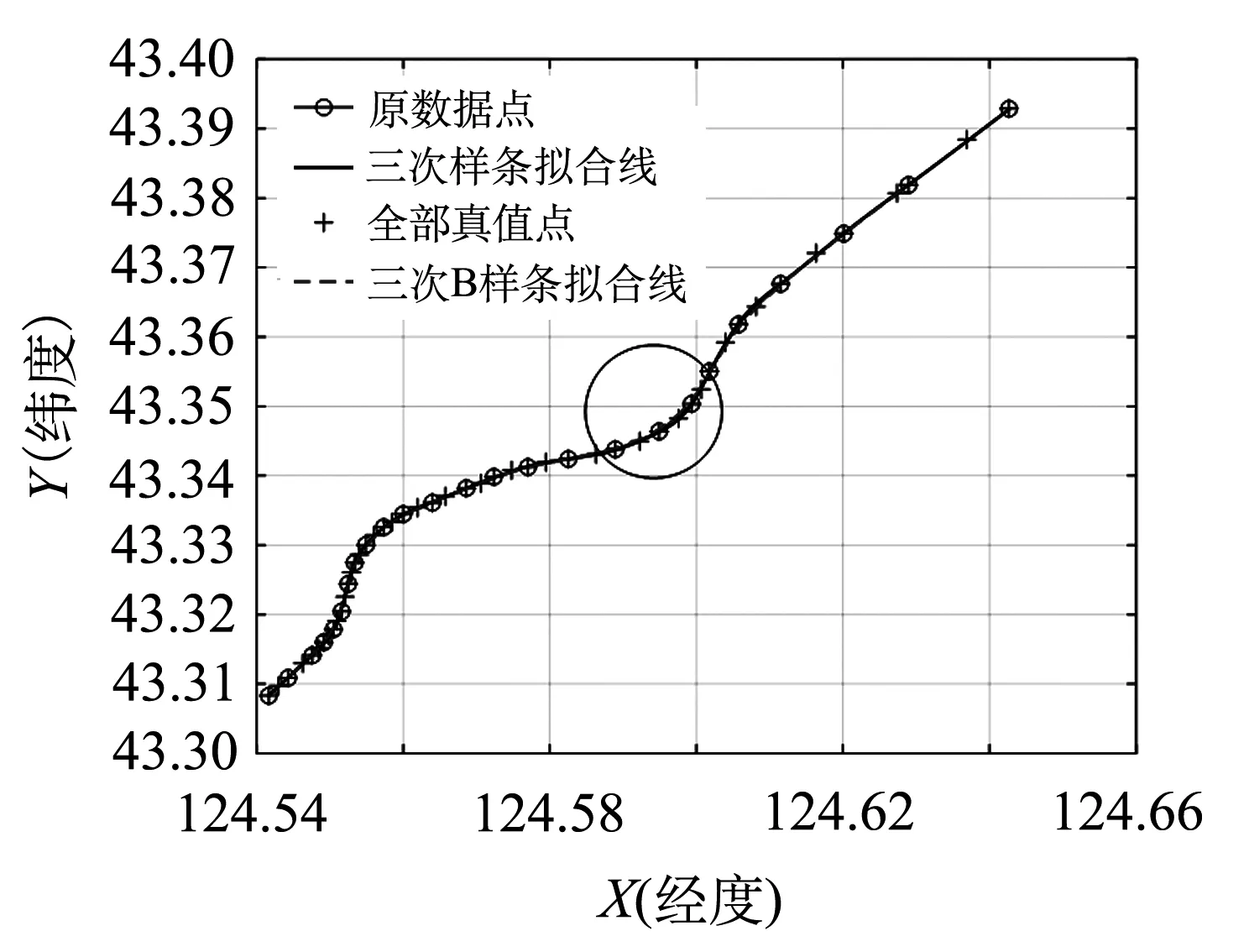
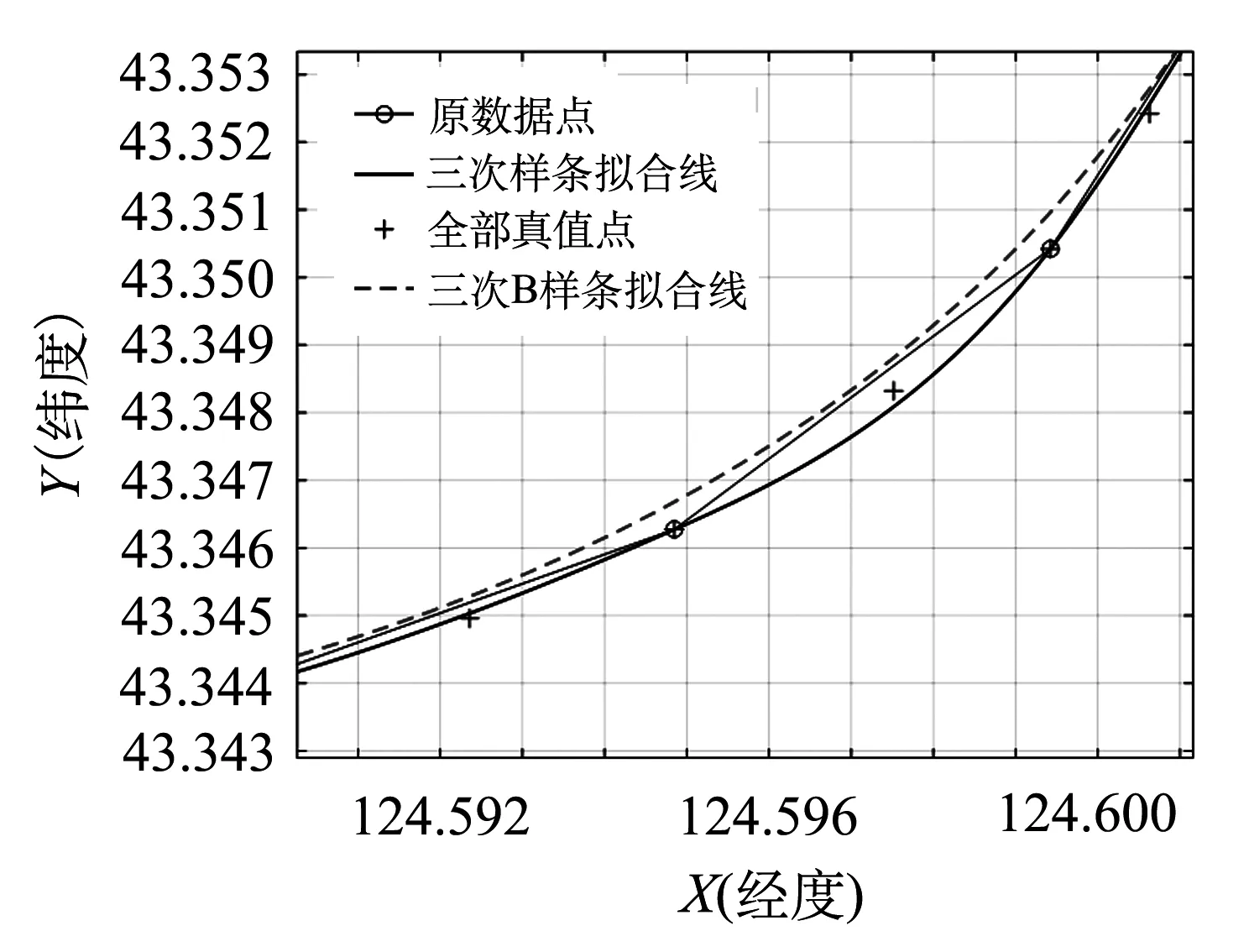
4.2 插值仿真
5 结论

