基于改进CART算法的M-learning过程中知识掌握程度预测
唐 立,李六杏
(安徽经济管理学院 信息工程系,安徽 合肥 230031)
M-learning是moblie learing的简称,通常被译成移动学习,它是指利用智能终端设备 (如手机、PDA等)进行的远程学习[1].随着移动计算机技术不断地发展,移动智能终端设备几乎是每个人必有的设备,M-learning的学习方式是现代教育发展新的阶段,它越来越多地受到国家和教育界的重视.在《国家中长期教育改革和发展规划纲要(2010-2020年)》的指导下,M-learning作为教学辅助越来越多地被应用在高校的教学系统平台上,如翻转课堂,基于M-learning实验平台,基于MOOC的M-learning平台等[2].M-learning的出现,试图把传统的“教-学”模式改变成“学-教”模式,目的是为了提倡个性化教学,把教学精确服务到个人,使得教学效果大幅提高.而使用数据挖掘技术对M-learning进行挖掘分析,试图通过数据挖掘发现一些规律,预测学习效果,为个性化教学提供可靠的依据,采用先学后教即“学-教”模式,精准地把教学服务落实在每一个受教育者的身上[3].
数据挖掘技术在教学中的应用相当广泛,有很多专家和学者发表过相关的学术论文,如:攀妍妍将ID3决策树算法用于对学生在线学习信息的挖掘,找出影响学生学习效果的分类规则[4];范洁把C4.5算法应用更在在线学习行为评估系统中[5];谢修娟运用Fayyad和数学等价无穷小改进C4.5,提高运算速度,应用于E-learning教学辅助系统中[6];赵强利提出基于选择性集成的增量学习的在线学习模型,针对监督学习和分类问题,提出处理集成问题的相关算法[7];董彩云在教学系统中用关联规则挖掘算法,找出影响学生学习兴趣因素[8].
在学习和参考了多位学者研究成果前提之下,根据M-learning实际情况,把CART算法进行改进,构建一个以M-learning过程数据预测知识掌握程度的分类决策树模型,用于对学生知识掌握程度的预测,目的是为个性化教学提供依据,把更有针对性的教学服务于学生.
1 CART算法的概述
CART(Classification And Regression Tree)是一种二叉树形式的决策树算法,二叉树算法只把每个非叶节点引申为两个分支,它的结构比ID3和C4.5算法结构更简洁,易于理解.CART构树原理,先对样本数据进行二元分割成两个子集,对子集再分割,自顶向下不断递归生成树,直至分支差异结果不再显著下降,分支没有意义了,则树建成.由此可以看出决策树生长的核心是确定分枝标准,对于CART算法来说,它的分枝标准是从众多分组变量中找到最佳分割点,其方式就是用Gini指标来表示数据纯度.
1.1 Gini指标
Gini指标是样本杂质度量方法,假设一个样本共有G个类,那么节点L的Gini不纯度可以定义为:

其中pg为样本点属于第g类的概率.直观来看,Gini指标反映了数据集中随机抽取两个样本,其类别标记不一样的概率,也就是Gini越小,当前数据纯度就越高.
假设集合L在A条件下分成L1和L2,那么集合L的Gini指标定义为:

在划分属性时,选择使得划分后Gini指标最小的属性为最优属性,并以此为分支准则建树.
1.2 连续属性与离散属性处理方法
(1)对于离散属性.CART算法对离散属性分各值的不同组合,按不同组合将其分到树的左右两枝,对所产生的树进行Gini指标判定,从而找出最优组合项.如果只有两个值,那么就只有一种组合;如果是多属性(X1,X2,X3),则会产生(X1,X2)和 X3、(X1,X3)和 X2、(X3,X2)和 X1的 3 种组合.这是因为 CART 遵循着二元分割特性.对于n个属性,可以分出(2n-2)/2种组合情况.
(2)对于连续属性.CART算法对连续属性,先进行属性按值排序,分别取相邻两个值的平均值作为分割点,二分成左右两树,计算Gini指标,判定最佳分割点.对于连续属性分割一般运算量都比较大,本文后面章节将进一步介绍.
1.3 分类决策树建立步骤
S1:计算已有样本L的Gini指标值,利用公式(1)选择最小Gini指标作为决策树的根节点.
S2:整理样本集合的所有的子集组合,对于离散属性,计算所有子集得出最小Gini指数,对于连续属性,进行最佳分割阀值离散化.
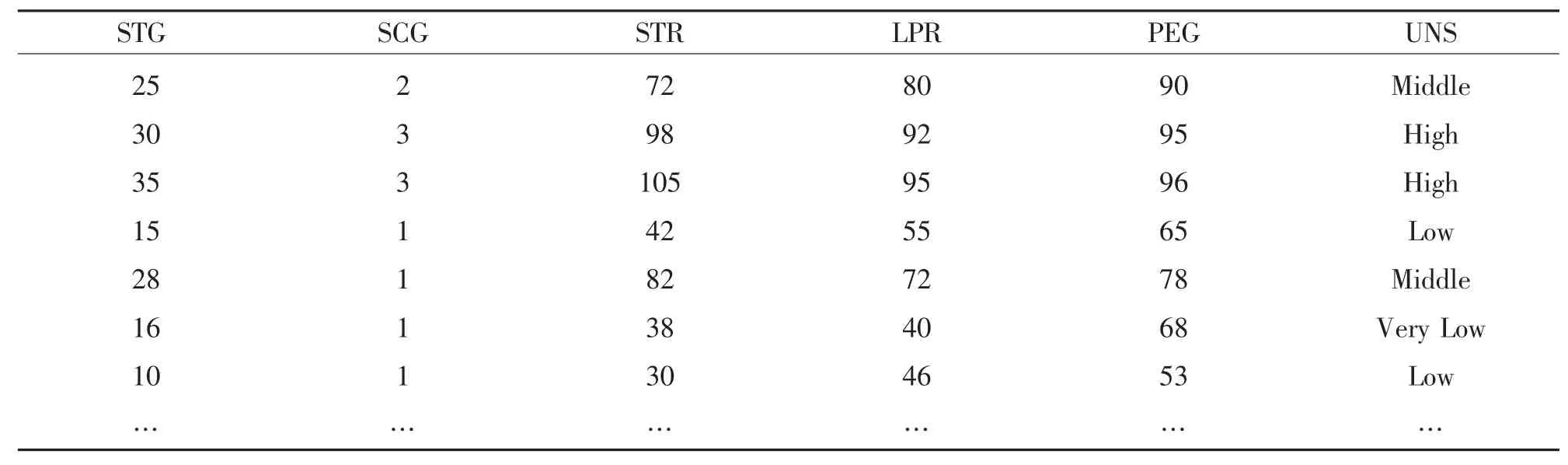
S3:对连续属性每一特征A,对它可能取值a,可以划分A≥a与A S4:找出对应Gini指标最小Gini(L,A)的最优切分特征及取值,并判断是否切分停止条件,否,则输出最优切分点. S5:递归调用S1-S4. S6:生成CART决策树. S7:防止模型过拟合,利用损失矩阵剪枝法进行剪枝,简化决策树. 传统CART算法在处理连续属性离散划分过程比较复杂,运算量比较大,同时对小量样本数据的预测精度比较低.为了弥补这些不足,本文提出首先利用Fayyad边界点判定定理减少CART算法对连续属性最优阀值运算量,然后用GB算法把弱预测器迭代成强预测器,提高小量样本数据预测准确度. 传统CART算法在对连续属性离散化时,先样本L所有的属性按值要进行排序,如得到L1,L2,L3,…,Ln,然后对每个相连的属性值的平均数进行分割,这样就对L的N个属性值产生了N-1个分割点,最后对每个分割点进行计算Gini指标值,得到最小的Gini值的属性就是L的最佳分割点.经常遇到连续数据值的个数是非常大的,会产生大量的分割点,使得运算量变大,减低了决策树生成的效率.利用Fayyad边界点判定优化连续数据值分割次数,提高对连续属性离散化的效率. Fayyad边界定理[9],首先将样本集L按照连续属性值X进行升序排序,假设存在相邻的数据L1,L2,只要满足 X(L1) 边界定理表明,对于连续属性划分分割阀值点,是找出两个相邻且不容类别的边界点上,然后计算出前后两个相邻点的属性平均值.例如对样本数据L按X属性升序排序{L1,L2,L3,…,L10},进行Fayyad边界划分分割阀值点,只需要5次分割值点运算Gini值.而传统CART算法的连续属性处理方法,则需要对数据L进行9次分割值点运算Gini值.可以看出利用Fayyad减少分割值点运算次数. 传统的CART算法本身就是一种大样本统计方法,对异常数据抗干扰性强,泛化能力强,但是遇到一些样本量相对比较小时,模型就显得不稳定,容易忽视一些小量数据,形成弱预测器,造成预测错误.本文提出GB算法,能够使CART算法重复利用小量样本数据,集成多个弱预测器生成强预测器,建立更为稳定的预测,从而提高了CART预测精确度. GB算法是一种解决分类问题的机器学习算法,它是属于Booting算法的一个分支.其原理是,首先对每组样本赋予相同的权重,通过对一组样本训练建立一个弱预测器;其次利用弱预测器进行预测,对预测结果进行样本权重调整.如果预测精度较高,降低样本权重,如果预测精度低了,则增加样本权重.最后,把不断训练和权重调整过程中的一系列预测器和权重值集成形成强预测器,从而提高预测精确度[10]. 算法具体如下: 间划分为迭代次数为k的不同区域为S1t,S2t,S3t,…,Skt,其中T为迭代次数,CART叶子数为K. 首先对模型初始化: 然后计算伪残差: 计算 Zt(a)的系数 γkt: 最后更新模型: 从GB集成CART算法中看出,GB算法就是建立的每一个弱预测器都在上一个弱预测器损失函数 L(b,F(a))的梯度方向,这样使得模型不断更新和改进[11]. M-learning过程是学生对基础知识认识和掌握的过程,从学生用户进入系统,相关数据就会产生,系统后台收集学生学习数据,存储在用户信息库中,然后再从信息库中提取学生学习数据进行预测分析.本文数据来源是通过M-learning对《Flash设计》课程中第五章节遮罩层的学习行为数据,因为条件有限,只对一个班级68位学生进行数据采集,所以只能对共计68条少数据量用以建立决策树模型和预测测试.目的是预测通过M-learning学生对相关知识点掌握程度,数据通过5个维度来衡量知识的掌握程度[12-13],分别是:STG:学习当前章节知识的学习时长;SCG:对当前章节知识的重复学习次数;STR:储备知识的学习时长,即之前章节学习时长;LPR:储备知识的学习在线测试成绩;PEG:当前章节知识的考试成绩.最后我们通过课堂测试和完成项目程度综合测评知识的掌握程度UNS,它有4个水平,即Very Low、Low、Middle、High.数据见表 1. 表1 预处理后的部分数据 为了保证数据的完整和一致性,对数据进行如下处理: (1)时间数据是比较复杂的,而实际得到的数据大多数以秒为单位,导致运算数据量增大.通过测试,在不影响精确度的前提下,我归化时间为分钟.因为时间太精细对于构建知识掌握程序模型并没有意义,同时这样大大降低数据复杂度. (2)对于在线成绩数据缺失问题,为了保证精确度,将其数据过滤掉. (3)学生在操作学习平台软件时可能出现异常操作,对重复学习次数设定阀值,出现学习次数超过阀值,或者单位时间内出现的学习次数过多等异常情况,进行及时筛除,排除数据异常. 对表2中46组数据建立Fayyad-GB-CART模型,对其余22组数据进行模型验证.使用Python程序进行实验,首先对表2连续属性Fayyad分割,以STG,SCG,STR,LPR,PEG为条件属性,UNS为决策属性,建立GB-CART模型决策树模型.在此同时依据混淆矩阵法剪枝,修剪一些干扰枝,防止过于拟合,得到更简单的决策树.决策树的建立运用if-then形式表示分类规则,其形式如同: (1)If STG<19&&SCG<2&&… then UNS=Very Low (2)If 20= (3)If STG>=30&&STR>=91&&PEG>=92&&… then UNS=High ……. 为了方便分析,利用改进的CART建立好模型后,和传统的CART建立好模型,在本实验中对其余22组数据进行预测测试,获取预测的UNS等级,与实际情况的准确率比照见表2.改进的CART算法每类预测明显精确度比传统的CART算法要高很多. 表2 传统CART与改进CART预测准确率比较 Fayyad-GB-CART模型建立中,对模型迭代次数设定为46,通过不断迭代更新模型的精确度.对UNS等级为Middle分类的迭代次数与精确度的关系见图1. 图1 Middle等级的迭代次数与精确度 随着迭代次数提升,精确度也随之缓慢提高.对于小样本数据通过Fayyad-GB-CART迭代是可以提升其精确度的.改进的CART算法建立的模型具有有效性,可靠性和准确性. 把决策树算法运用到M-learning教学辅助中,可以根据学生M-learning过程中的学习行为和成绩数据,较为准确地预测学生对知识点掌握程度,首先可以及时预警告学生,让他做出自我调整.其次教师依据统计整个班级预测情况及时准确地更正课堂教学计划.例如整个班级知识点掌握预测普遍LOW等级,这时课堂上教师就要把原计划项目化制作修改为知识点巩固教学.最后教师可以针对个别学生情况,线上或课堂进行个性化辅导. Fayyad边界法减少CART算法分割阀值点运算次数,GB算法提高了小量样本数据的精确度,本文集合Fayyad边界和GB算法,改进了CART算法在连续属性和小样本数据特殊情况下的使用,并使之运用在M-learning教学辅助中,以《FLASH设计》中遮罩层知识掌握程度做实验,对采集的68条数据进行建模并预测,实验证明改进的CART算法不仅速度有所提高,精确度也提高很多,但是依然还存在一些不足. (1)GB算法下CART模型建立提高了预测精确度,但模型计算量随着迭代次数而增加,迭代次数的权重设置是一个需要进一步研究的点. (2)改进的CART算法大多针对小样本数据量给建立带来不稳定性而提出的,遇到的情况是属于特殊情况下采用的方法,只针对小数据效果明显.如何改进大数据量的运算精确度将是下一步需要研究.2 改进的CART算法
2.1 改进运算速度
2.2 改进CART预测精度


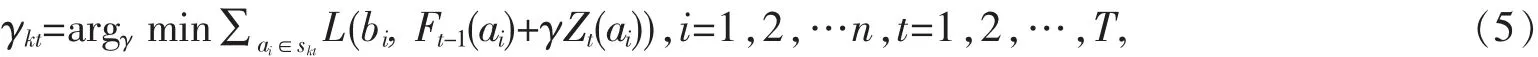
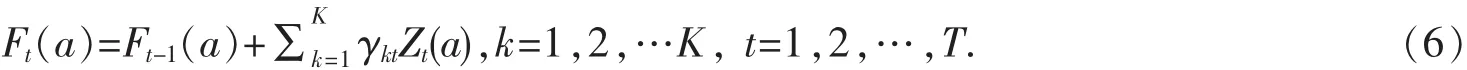
3 基于改进CART算法的M-learning
3.1 样本数据
3.2 建立CART决策树模型
3.3 改进算法的有效评估


3.4 系统中知识点掌握程度预测
4 结语

