关于正测度集上无界发散的Fourier级数

罗仕乐，郭星东

（韶关学院 数学与统计学院，广东 韶关512005）

Fourier级数［1-2］在分析学中有着重要的地位，Fourier变换［3-5］在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用［6-7］.Fourier级数展开的主要思想是用相互正交的正弦函数和余弦函数作为基函数去表示具有周期性的一般函数.对于Fourier级数中Fourier系数的表示形式，一般是在Riemann积分［8］和Lebesgue积分［1］两种不同意义下给出的，由于积分意义的不同，会导致所得到Fourier展开的相关性质有所不同，和Riemann积分对比，Lebesgue积分定义的Fourier级数有着更好的性质以及更广泛的应用.

对于Lebesgue可积函数的Fourier级数收敛判别，已经有了很多已知的结果，比如经典的Jordan判别法、Dini判别法、Young判别法等［4-6］.根据这些判别法，满足一定条件下的函数的Fourier级数是收敛的.为了更好地探索Fourier级数的收敛行为，笔者考虑另一个极端也就是发散情形，探索正测度集上几乎处处无界的Fourier级数存在性，丰富Fourier级数收敛性的相关研究.

在后续讨论中，用L(E)表示E上的Lebesgue可积函数空间，U(x,δ)表示以x为心、δ为半径的开区间，表示集合E的闭包，m(E)表示集合E的Lebesgue测度，O(α)表示与α的同阶无穷大，其中α→∞.

引理［1］（Riemann-Lebesgue）设 f(x)∈L［a,b］，则：

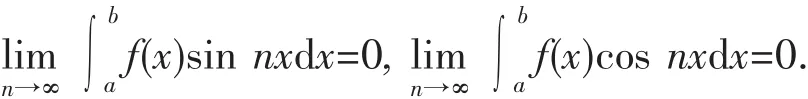
定理 设E是有界闭集，且mE>0，则存在函数f∈L(E)，使得f的Fourier级数在E上几乎处处无界并且发散.

证 为了以下Fourier级数叙述的便利，不失一般性，可设E=［0，2π］.p2,p3,…,pn是奇数，记：

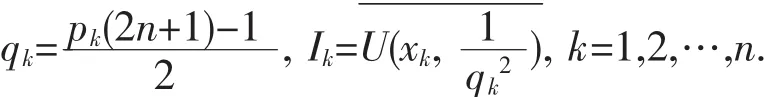
定义函数：

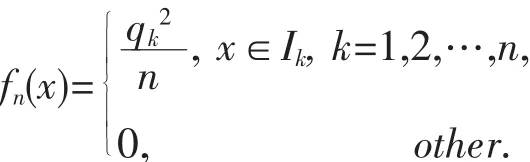
显然，fn(x)是E上的非负有界变差函数，并且有

这表明f(x)的Fourier级数在［0,2π］上几乎处处无界并且发散.证毕.

本文构造了一个正测度集上几乎处处无界并且发散的Fourier级数，从新的角度讨论了Fourier级数的收敛行为，得到的结果丰富了Lebesgue可积函数的Fourier级数收敛结果.