基于协差阵向量半范数的典型相关分析及其在量化投资中的应用
杨玉锋,林伟城
(韶关学院 数学与统计学院,广东 韶关512005)
随着金融行业的高速发展,各类证券和期权类产品种类增多,交易量大增,很多模型已经不适合当今市场行情,随之而来对量化投资[1-2]的研究变得越来越重要.量化投资是指借助现代统计学、数学的方法,从海量的历史数据中寻找能够带来超额收益的多种“大概率”策略,并纪律严明地按照这些交易策略所构建的数量化模型来指导投资,以减少投资者情绪波动的影响,力求取得稳定的、可持续的、高于平均的超额回报.资金流向能够帮助投资者透过指数(价格)涨跌预测到其他投资者的投资行为,并对此做出相应的应对策略.在金融交易系统中,一般能获取收盘价、最高价、最低价、开盘价、持仓量、时间、成交金额以及成交量等数据,如果能通过统计分析找出这些数据之间的相关性,将对制订有效的量化投资策略有着重要的指导意义.典型相关分析[3-4]是研究两组变量之间相关关系的一种多元统计方法,能有效地揭示两组变量之间的相互线性依赖关系.
在多元统计分析中,协差阵[3]扮演着重要的角色.笔者利用协差阵的对称半正定性质,引入向量半范数[5]推导典型相关分析,并把结果应用到量化投资的回归模型中.在后续讨论中,用‖·‖2表示向量2范数.
1 基于向量半范数的典型相关分析
定义[5]设 p(x)是定义在 Rn上的一个非负函数,满足:(i)p(αx)=|α|p(x),∀x∈Rn,α∈R;(ii)p(x+y)≤p(x)+p(x),∀x,y∈Rn,那么称p(x)是Rn上的一个半范数.
定理 设A∈Rm×n是对称半正定矩阵,那么定义了一个Rn上的半范数.
证 首先,当∀x∈Rn,α∈R时,有:
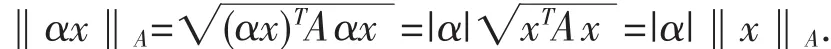
由于A是对称半正定矩阵,因此存在正交矩阵Q以及对角元非负的对角矩阵D,使得:
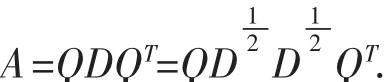
则当∀x,y∈Rn时,有:

因此有:

基于定理结果,可以利用该半范数给出随机向量的典型相关分析理论.
设x,y是两个n维随机向量,a,b∈Rn,典型相关分析需要讨论x,y线性组合aTx,bTy的相关性,即计算相关系数:

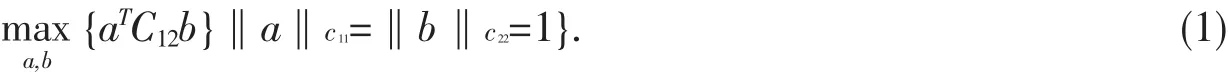
注1 (1)式定义的最优化问题形式比文献[3]的形式更简单,并且约束条件的意义更为直观.
2 量化投资的回归模型
量化投资问题中,能获取收盘价、最高价、最低价、开盘价、持仓量、时间、成交金额以及成交量等交易数据,在对交易数据进行回归分析[6]的过程中,关键在于选择相关性较大的变量进行组合,进而结合典型相关分析完成回归分析.接下来对(1)式的目标函数进行推导.
由 Cauchy不等式和谱分解定理[7],有:
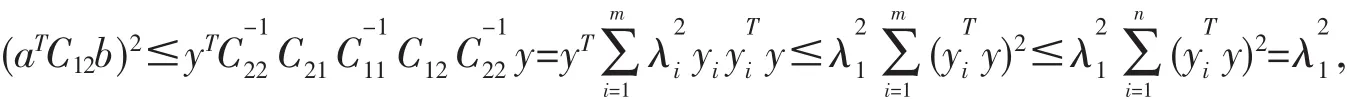
其中y∈Rn是矩阵的m个正特征值λ1≥λ2≥…≥λm>0对应的单位特征向量.另一方面,令:

其中a1,b1∈Rn分别由以下两个线性方程组求解得到:

简单计算可得:
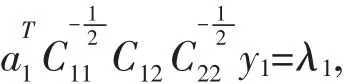
这表明由(2)式给出的a1,b1可作为典型相关向量的线性组合系数.因此由约束最优化问题(1)可得到的第一对典型相关变量为:

注2 由于C11,C22是C的主子阵,因此均为半正定矩阵,从而(2)式中两个线性方程组可采用MINRES方法[8]进行求解.另一方面,由于对称性,计算主特征向量,可利用幂法结合Rayleigh商加速技巧进行[9].
根据上述讨论,可以给出基于半范数典型相关分析的量化投资回归模型:
①对收盘价、最高价、最低价、开盘价、持仓量、时间、成交金额以及成交量的数据进行规范化;
②按定义计算上述变量的样本协差阵C;
④用MINRES方法求解(3)式中的两个线性方程组得到a1,b1;
⑤按(4)式计算第一对典型相关变量u1,v1;
⑥按u1,v1的系数比例分配进行回归分析,并做检验;
⑦对回归分析结果进行背景解释.
3 结语
本文利用样本协差阵的对称半正定性质,结合向量半范数理论建立了典型相关分析的约束最优化问题,并通过推导得到第一对典型相关变量,最后结合回归分析给出了量化投资的数学模型.
半范数的引入得到了简化的约束最优化问题,使得后续典型相关变量的推导更为直观,类似的推导思路可以根据实际需求推广到更深层次的典型相关变量的求解中.

