一种改进的SPRINT算法

白玲玲，韩天鹏

（1.中共阜阳市委党校 教务处，安徽 阜阳 236034；2.阜阳师范学院 计算机与信息工程学院，安徽 阜阳 236037）

共享在互联网和无线网络上的微博、个人博客、基于Web 2.0的图片和视频产生了大量的数据；其中存储在半结构化XML文档、HTML文档和非结构化的照片、音频和视频中的数据也日益丰富.同样网络搜索、商业销售、生物医学、自然观察和科学计算等领域也都有大量的数据［1］.这些数据类型多样，具有规模大，变化速度快、分布式存储、异构性、半结构化或非结构化等相同特征.基于数据流的离群挖掘算法并不能完全满足满足获取、管理、分析和理解大量快速变化数据的需要，数据密集型计算就是在这样的背景下营运而生［2-3］.

聚类是数据挖掘中最重要的技术之一，它旨在将物理或抽象主体与相似主题相关联.Jiang等人提出了在 MapReduce中使用 k-means聚类算法，并通过 MapReduce［4］实现了 k-means［5］算法的转换.Hong 等人提出了DRICA（动态粗糙增量聚类算法）作为解决数据更新问题的一种方法，确保了算法的稳定性并克服了在所有数据上实现算法的低效率［6-7］.

频繁项目集挖掘是关联规则挖掘，序列模式挖掘，关联挖掘和多层次挖掘的最基本和重要的过程［8-9］.Apriori挖掘算法基于云计算，在事务集和基于MapReduce模型的项目集上实现双重二进制编码，该算法只需要布尔AND和OR运算，效率较高［10］.Li等人提出了基于闭项目集挖掘算法的CMFS算法，该算法使用约束最大频繁项集深度优先策略和修剪算法［11］.Hong等人提出了FIMDS算法，该算法可以从分布式数据中挖掘频繁项集，使用频繁模式树结构来存储数据，有助于从每个部分模式树（FP-tree）根获取项目组频率［12］.

离群数据挖掘是数据挖掘中使用的主要方法之一.异常值是一个与其他数据对象不同的数据对象，由不同的机制产生的［13］.数据密集型计算中的大多数离群挖掘算法涉及扩展和改进经典离群值挖掘算法.最近，提出了许多基于数据流的传统异常值检测算法.由于时间复杂度高，责任响应速度尚未达到，结果误差较大，准确性不理想.异常值检测算法应用于数据的研究仍处于初级阶段.对数据密集型计算环境中异常值检测的研究具有重要意义.Pan利用基于Hadoop平台的SPRINT算法，采用并行方法构建决策树，然后解决Hadoop平台中的并行问题.

1 基本算法分析

Shafer等人在1996年提出了基于SLIQ的SPRINT决策树算法［20］.SPRINT算法结合了属性列表和类别列表.属性列表用于存储属性值，直方图用于记录指定节点前后部分的分类分布，并使用散列表代替SLIQ来记录属性子节点的属性值，训练元组的形成.属性列表和组织图数据结构不需要存储或存储器，这消除了存储能力的大小限制.SPRINT算法不仅简单，准确，快速，还改善了数据结构，这使挖掘问题更容易解决.

SPRINT算法使用属性列表和直方图来帮助计算最佳分割点和分割属性.属性列表的每个元组都由数据记录索引，属性值和类别ID组成.在SPRINT算法的初始化中，为每个属性创建一个属性列表，连续属性的属性列表需要根据其属性值进行预先排序.

随着节点被分成子属性列表中的子节点，当前节点维护的属性列表将被扩展.每个节点都维护一个直方图，计数矩阵，散列表等.直方图用于描述所选连续属性划分的分类分布信息.计数矩阵用于确定分类的数量和属性值的离散属性的节点选择的属性列表的关系.直方图和标记矩阵用于支持基尼指数的计算.哈希表记录拆分后的最佳拆分属性和可用子节点信息；然后，用于帮助分割其他属性列表.

对于特定节点，在确定最佳分裂属性及其分裂节点之后，可以直接在子节点之间划分与该属性相对应的属性列表.由于不同特性列表的序列不同，不能直接划分.相反，在划分其他属性列表之前，应该从节点的最佳分割属性及其分割点信息生成散列表.哈希表用于记录节点所在的子节点，还用于分割其他属性列表.

2 算法的改进

2.1 改进算法的数据结构

属性列表具有与SPRINT算法相同的功能：它用于记录分配信息.训练数据集根据初始化期间的属性分解为独立的属性列表.每个属性列表由属性值，类别值和索引值组成.属性列表的数量取决于属性的数量.最初，根节点用于维护整个属性列表.与连续属性对应的每个属性列表都已预先排列，并且随着节点数量的增加，属性列表将被拆分.分割属性列表属于相应的子节点.

直方图用于描述类分布，并对应于SPRINT算法中决策树中的树节点；它的结构与M-BCBT算法中的直方图不同.直方图用于计算属于树节点的最佳拆分属性及其拆分节点.为了利用MapReduce编程框架，对直方图结构进行了一些更改.数据被分成几个块并存储在群集环境中，以便与MapReduce进行数据处理.直方图用于记录属于每个数据块扫描节点的属性值分布.对于连续属性，每个数据块都有两个对应的直方图，即Cbelow和Cabove，它们取决于当前数据块的属性列表中的扫描位置.Cbelow表示a≤R的类分布条件的所有记录，而Cabove表示a>R的类分布条件的所有记录，其中参数a是扫描值的连续属性，R表示最佳分割值.每个直方图记录由数据块索引和所有类记录组成.

2.2 M-BCBT算法描述

Master Server中构建分类器的核心程序包括启动，规划和控制整个决策树模型.一系列在Slaves上运行的MapReduce任务用于计算拆分属性和属性列表的拆分.核心流程是维护一个全局决策树.全局决策树用于保存已建立的部分.Build Classifier程序流程如下：

Require：NodeQueue NQ，TreeModel TM，Training record

（x，y）∈D， Attribute set Att

Troot=new Node

Initiate（Troot， D，Att）

TM=Troot

NQ.push_back（Troot）

BuildTree（NQ）.

在最初阶段，核心程序根据预处理属性列表中的信息建立根节点.然后，将根节点添加到全局节点队列中，并调用构建树功能以创建队列节点的子树.BuildTree的程序流程如下：

Require：NodeQueue NQ， TreeModel TM， Training record

（x，y） ∈D

For each Tcurr∈NQ do

If JudgeLeaf（Tcurr） is false then

bestSplit=FindBestSplit（Tcurr）

Tcurr→splitAtt=bestSplit→splitAtt

If bestSplit→splitAtt is category then

Tcurr→leftAttSet=bestSplit→leftAttSet

Tcurr→rightAttSet=bestSplit→rightAttSet

Else Tcurr→splitValue=bestSplit→splitValue

parationTrainingSet（Tcurr→D， leftD， rightD）

remove（Tcurr→splitAtt）

Create new nodes Tleft，Tright

Initiate（Tleft， leftD，Att）

nitiate（Tright， rightD，Att）Tcurr→left=Tleft

Tcurr→right=Tright

NQ.push_back（Tleft）

NQ.push_back（Tright）

Else Tcurr→isLeaf=true

Tcurr→label=y.

每个非叶子节点只有两个分支，在决策树模型中只执行二分裂.在构建决策树的过程中，Tcurr表示从全局节点队列中提取并按顺序处理的树节点.首先，需要检查Tcurr是否是叶节点.如果训练数据元组Tcurr是“纯”（全部3个组件属于同一个类别）或者训练数据元组的数量达到用户定义的阈值，则Tcurr标记为叶节点.在第一种情况下，每个节点根据它所属的类别进行标记.在第二种情况下，每个节点所属类别的数量被用作标签.其次，核心计算拆分节点并选择最佳拆分属性.Tcurr根据最佳分割信息和分割属性进行标记.训练集用于将Tcurr的属性列表分成左侧和右侧，用于生成子树Tleft和Tright.然后，Tleft和Tright被添加到全局节点队列中.队列NQ中的节点被迭代删除.当队列为空时，程序结束并且决策树模型完成.

2.3 计算最佳分割点

计算最佳分割点的算法与SPRINT算法类似，并涉及扫描连续属性计算分割点或离散属性技术矩阵的属性列表.该算法采用MapReduce技术实现了最佳分割点的并行处理，提高了算法的效率.假设N个Mapper任务用于处理扫描统计信息，以便每个Mapper任务只处理训练数据集的1/N.信息汇总和分割点计算通过Reducer执行，它返回最佳分割信息和分割属性.

算法的主要优点是它只需要计算每个数据块的类别分布.该算法执行一系列MapReduce任务来构建当前树节点的直方图和块直方图.然后，它计算基尼指数以确定每个最佳分割点.FindBestSplit算法的Mapper部分和Reducer部分的描述分别如下：

Mapper算法：

Require：Current node Tcurr，Attribute set Att，Class set Y

For each A∈Att do

Class Count array countY for Y

Index=firstreCord（Tcurr→D）

For all（x，y）∈（Tcurr→D，Attribute list of A） do

county［findY（Y，y）］++

Output（（findA（A）），（Index， countY））.

Reducer（ ）算法：

Require：Key k， Value Set V， Attribute set Att， Class set Y

For All k do

If Att［k］is continuous then

For all distinct values∈V do

If sameBlock（value ［i］） then

Output（（k），（value ［i］， sumCount（value ［i］）））.

上面的伪代码在FindBestSplit的Map阶段描述了Mapper任务.每个映射器独立收集每个数据块的类别分布信息，并输出一个密钥表，其中密钥为属性索引的属性下标索引，其值由数据块序号和类别关键值组成.

3 结果分析

3.1 实验环境的构建

实验在Hadoop 0.20.2分布式平台上进行，该平台由9台PC机组成，具有2.93 GHz的CPU，2 GB内存，200 GB硬盘和Red Hat Linux操作系统.Eclipse3.3.2是一个开发工具，其中一个是服务器节点，另外八个是数据.

UCI数据库是数据挖掘的主要数据源之一.本实验使用UCI数据库中的KDD Cup 1999数据集，该数据由4 000 000条记录和40个属性组成，其中34个是连续属性，5个是离散属性，1个是类标记属性（离散属性）.

3.2 实验结果及分析

为了分析M-BCBT算法的性能，笔者评估了时间效率，可扩展性，并行性和准确性.实验数据是重复实验的平均值.操作时间由算法运行时间，I/O通讯时间和数据预处理时间组成.

在实验1中，比较了SPRINT和M-BCBT的计算时间，以评估时间性能并测试M-BCBT算法的可扩展性.通过使用相同的训练数据集和增加训练集的大小来比较SPRINT和M-BCBT的运行时间的趋势.对于每个实验，参数保持不变，操作时间见图1.

随着训练数据集的大小增加，M-BCBT的操作效率逐渐优于SPRINT的操作效率.当只有少量数据时，HDFS需要分割训练数据并将分布存储在数据节点中；M-BCBT的预处理时间远高于算法的运行时间，导致M-BCBT的总时间效率低于SPRINT.在数据集达到一定大小后，并行化使M-BCBT的决策树建立更高效，缩短了计算时间.与此同时，对于大型数据集，SPRINT算法的运行时间迅速增加.SPRINT算法对于大数据具有良好的可扩展性，但仍有许多限制，例如数据结构限制以及存储器中散列表和直方图存储的限制.M-BCBT算法使用MapReduce框架和HDFS分布式文件系统来提高算法的可伸缩性.

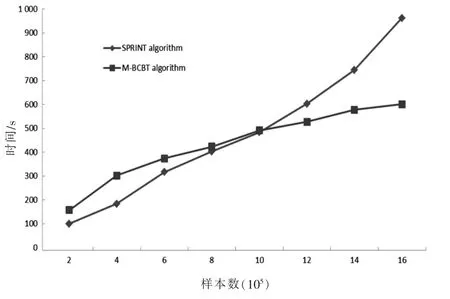
图1 训练不同大小数据集的操作时间

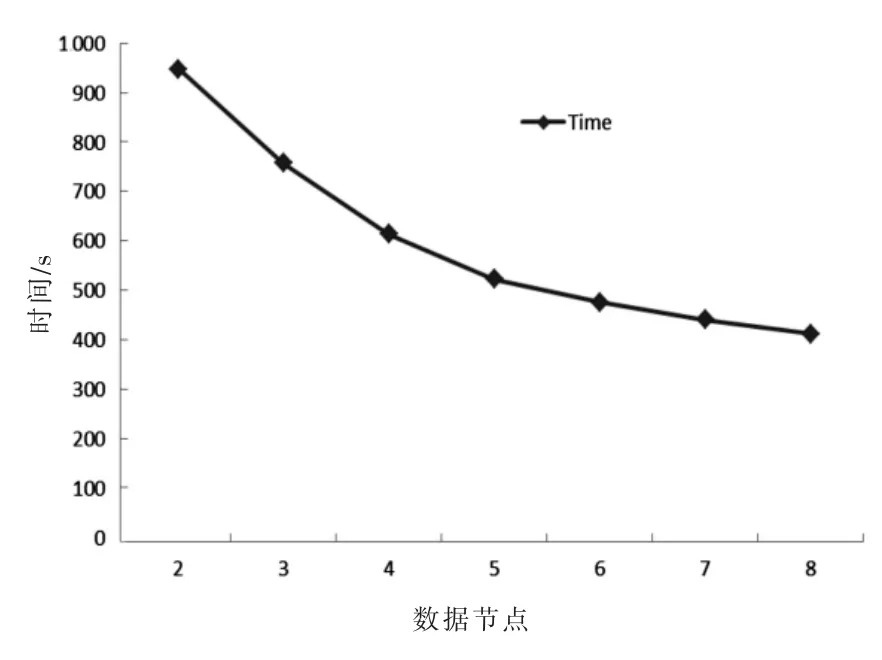
图2 算法运算时间随数据节点数的变化趋势

在实验2中，研究M-BCBT算法在并行总操作时间特性.在使用相同的训练数据集情况下，其会随着Hadoop聚类数据节点数量的增加而减少.算法的其他参数对于每个实验都保持不变.图2列出了多个观测值的平均值.随着聚类节点数量的增加，M-BCBT的工作时间呈指数下降.

在实验3中，考察了测试算法分裂点计算时间和属性表分裂的趋势.使用相同的训练数据集并保持其大小不变，Hadoop聚类数据节点的数量增加，并检查M-BCBT算法的MapReduce任务分割点计算时间和属性表分割时间的趋势.算法的其他参数保持不变.结果的平均值显示见图3.随着节点数量的增加，分割点计算时间线性下降，属性表分割时间线性增加.随着节点数量的增加，分叉点计算优化过程得到改善，算法的效率得到提高.然而，属性表拆分方法限制了算法在效率方面的改进.

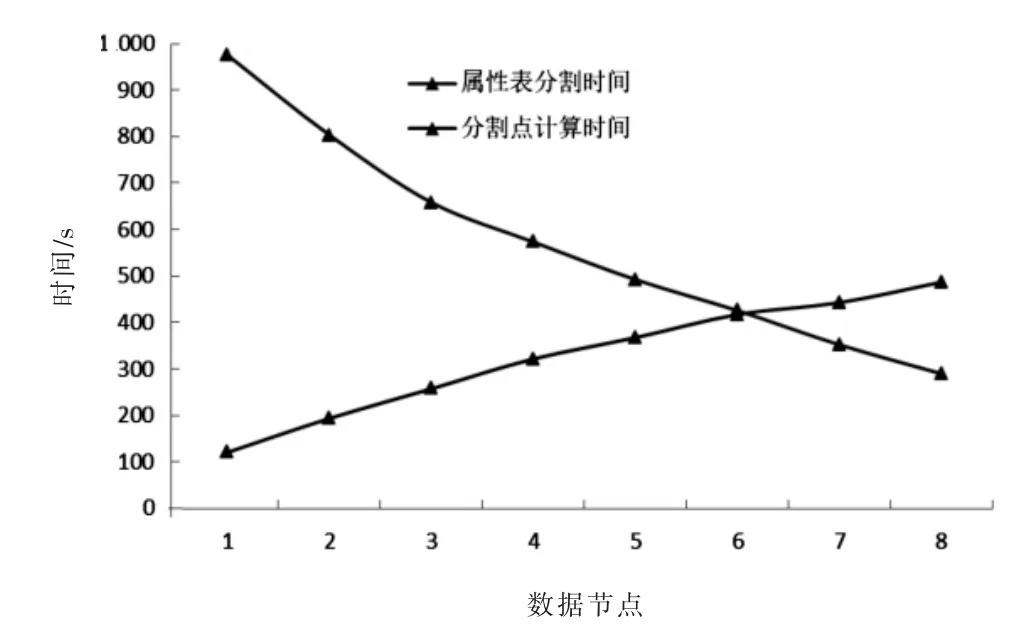
图3 属性表分割时间和分割点计算时间

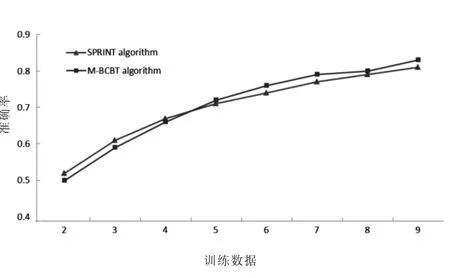
图4 M-BCBT算法的准确率趋势

实验4是M-BCBT算法和SPRINT算法的测试和精度比较.在这个实验中，Hadoop集群数据节点的数量保持不变，并使用相同的训练数据集.改变数据集大小，观察和比较M-BCBT算和SPRINT算法之间的准确度.对于每个实验，所有其他参数保持不变.观察结果的平均值见图4.与SPRINT算法相比，M-BCBT算法的准确度没有明显变化，并且随着数据集的增加，这两种算法获得相似的准确度，因为在M-BCBT算法中仍然采用精确查找技术，准确度不会受到算法框架变化的影响.

从结果来看，相同的M-BCBT精度会提高算法的时间效率.该算法具有良好的可扩展性，可满足海量数据的需求.但该算法的结构复杂，复杂性受到性能限制.

4 结语

随着大数据的发展，挖掘有用的信息已成为人们关注的主题.数据密集型环境只能在大数据挖掘研究的背景下考虑.目前对数据密集型计算环境中的数据挖掘算法的研究集中在改进传统的大规模聚类算法上.在本文中，引入了一种称为M-BCBT的决策树分类算法，该算法基于SPRINT算法和MapRe-duce计算框架，适用于数据密集型计算.通过实验测试了M-BCBT算法的性能.结果表明，M-BCBT算法具有良好的可扩展性和高水平的数据可用性.当大量数据时，大规模聚类的运行时间会减少.