基于Lagrange方程的长钢轨扣件回收机构动力学分析

陈水胜，吴博，鄢建明，胡伟明

基于Lagrange方程的长钢轨扣件回收机构动力学分析

陈水胜1，吴博1，鄢建明2，胡伟明2

(1. 湖北工业大学 机械工程学院，湖北 武汉 430068； 2. 上海铁路局 上海工务大修段，上海 200040)

针对一种长钢轨扣件回收机构的驱动特性研究，通过对其运动过程的势能变化分析，结合机构结构与驱动参数的关系，运用Lagrange方程求出驱动参数的显式解。结合机构的运动特性，应用Matlab对该机构进行动力学仿真，得出机构的动力特性曲线。为进一步研究在一定牵引功率下等效驱动连杆最佳的动力输出情况，分析不同结构下驱动力、驱动转矩的变化差异，得到结构变化对于机构动力的影响规律。研究结果表明：得到的动力变化曲线与实际作业工况相近。对类似机构动力特性的深入分析和结构优化设计具有重要的参考价值。

机构；驱动；Lagrange方程；动力特性；结构优化

目前，铁路轨道普遍采用钢轨扣件连接钢轨和轨枕，确保钢轨紧固定在轨枕上，并控制保持两股钢轨间距、钢轨轨面高差，阻止钢轨相对于轨枕的纵横向移动。据行业统计分析，铁路轨道每1 km下道的旧扣件至少有7 000 kg，传统采用人工回收装运的方式，劳动强度非常大，作业效率低，不适应铁路线路间密集空间，且存在重大安全隐患[1]。为解决上述问题，提出了一种铁路长钢轨换轨扣件收集装置的新型结构[2]，为进一步优化该装置的结构及驱动电机参数，以整个机构的力学系统为研究对象[3−9]，通过广义坐标系来描述机构运动，从而建立动力学数学模型，并分析在不同结构参数下机构驱动力与驱动力矩的变化。

1 机构运动描述及运动分析

该扣件收集装置由驱动电机、减速器、动平台和静平台组成。如图1，静平台主要由轨道平板车上安装的导向槽(11)，滚筒(6)，链轮A(5)，链轮B(12)和张紧轮(7)等组成。动平台(4)上装有轨轮(2)，料斗(3)，导向轮(9)及连杆(8)等结构件。传动链条(10)的一端通过转销连接在连杆(8)上，经链轮B(12)，张紧轮(7)和链轮A(5)后，另一端也用转销连接到连杆(8)上。在长钢轨(1)，滚筒(6)，导向槽(11)和导向轮(9)的约束下，通过链条(10)的拉力作用，实现动平台(4)的伸放和复位动作。当电机动力经减速器驱动链轮(12)顺时针转动时，在链条(10)的拉力作用下，可使动平台(4)收回到静平台上使其复位。当驱动链轮(12)逆时针转动时，可使动平台(4)伸出并使装有轨轮(2)的一端最终搁置到长钢轨(1)上面，从而进行物料回收作业。在实际应用中，结合铁路结构和功能要求，实际使用的回收装置可采用双排链传动结构，两组链轮传动机构布置于动平台的两侧，增加动平台的稳定性和可靠性。

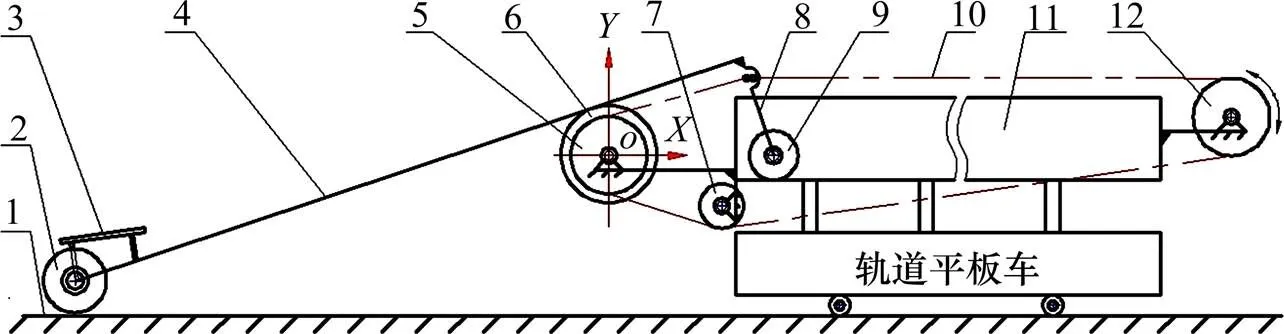
1—长钢轨；2—轨轮；3—料斗；4—动平台；5—链轮A；6—滚筒；7—张紧轮；8—连杆； 9—导向轮；10—链条；11—导向槽；12—链轮B

由于该装置动平台的伸放与复位过程的动力学特性是可逆的，本文选取该机构的复位过程进行动力学特性分析。假设扣件回收作业完成后，机构位置处于图2所示状态，在链条牵引作用下，复位过程完成可分成4个运动阶段，各阶段运动的结构特征见表1。为方便整个机构复位过程的描述，文中选取导向轮的运动轨迹作为机构复位各阶段的路线示意参考，如图2中轨迹路线1→2→3→4→5。在文中设定的位置坐标参考系中，以x轴正向为向右方向，其中动平台与刚性连杆刚性固连，在链条的牵引作用下动平台构件沿着切点跟随导向轮向右侧移动并有转动。

图2 机构复位动作阶段示意图

表1 机构各阶段的运动特征

为清楚表示复杂运动过程的动力学模型，便于系统动力学模拟[10−12]，和相应动力学控制研究[13]，以及清楚的表达出各构件之间的耦合特性[14−15]，基于该结构中系统动能与势能变化明显的特征，因而本文采取Lagrange方程法进行动力学分析。

2 拉格朗日动力学模型建立

2.1 广义坐标

为便于该收料装置机构动力学建模，综合考虑整个机构结构参数、各个部件的质量、质心分布和体积等因素，对机构的实际结构进行简化，各部件的简化说明方法说明如下。

1) 动平台主体钢梁和刚性连杆均视为矩形截面的钢梁；

2) 料斗视为集中作用于动平台身末端载荷，作为轨轮上的负载；

3) 动平台与链轮A内侧滚筒、导向轮与导向槽间无相对滑动，忽略其他接触阻力、阻尼；

以该机构静平台上的链轮A及其内侧滚筒转动中心建立平面坐标系，如图3所示，简化后的动平台部件用杆表示、连杆用表示。由于该机构实现复位的每个阶段的运动可视为移动、转动的合成运动，文中以整体机构的移动、转动的运动姿态来求解驱动力、驱动力矩的变化情况。链条直接带动连杆，因而视连杆为等效驱动件，当该驱动连杆的位置及姿态角确定之后，整个机构的运动也就确定了，因此取驱动连杆底部导向轮心点的水平位置，杆与垂直方向上的姿态角为广义坐标，即广义坐标q=()T(=1,2)。

2.2 机构动能分析

根据以上的简化分析，参照图3，设滚筒转动中心为坐标原点，即(0,0)，，和分别为轨轮、驱动连杆、滚筒与动平台的连接结点，为导向轮与驱动连杆的连接结点，其他符号标记如下：导向槽宽，导向轮半径，滚筒半径，轨轮半径1，动平台长，驱动连杆长1。则由各部分的几何关系可知各坐标点：(1sincos，1cossin+)，(1sin,1cos+)，(sin,cos)和(,)。因而由模型假设可知，驱动连杆的质心的坐标为(1sin2,1cos/2+y)，动平台的质心的坐标为(1sincos/2,1cos+sin/2)。

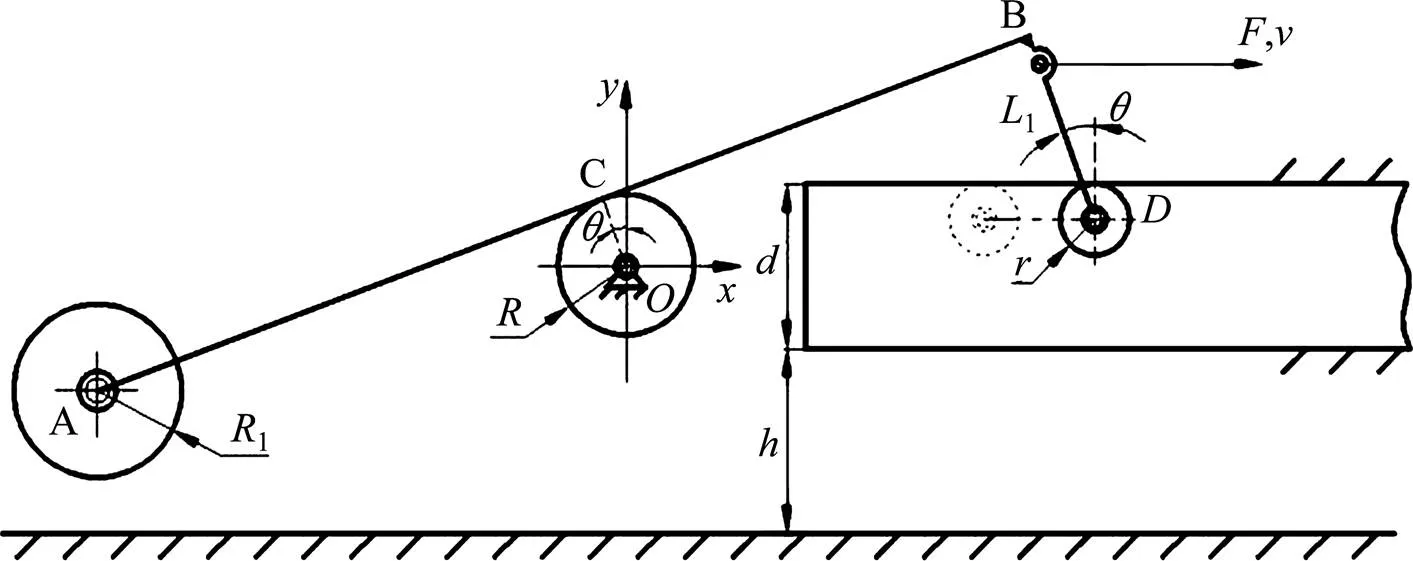
图3 机构的位置姿态图

由上述各坐标点，可分别求得扣件回收机构任意时刻各部分的运动速度，

导向轮的移动速度和绕轮心转动角速度分 别为

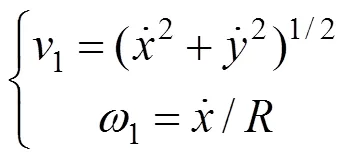
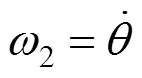
滚筒绕其转动中心的转动角速度

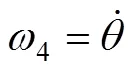
动平台的质量与截面宽分别是0和′，其等效转动惯量

导向轮的质量与等效半径分别是1和其等效转动惯量

1=12/2 (7)

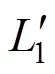
轨轮的质量与等效半径分别是3和1其等效转动惯量

3=312/2 (9)

滚筒的质量与等效半径分别是4和，链轮1的转动惯量

4=42/2 (10)

综合式(10)，该铁路扣件回收机构的动能E由动平台动能0，导向轮动能1，驱动连杆动能2，轨轮动能3和滚筒动能4之和组成，即：

式中：0为动平台的质量，kg；0为动平台的转动惯量，kg·m2；1为导向轮的质量，kg；1为导向轮的转动惯量，kg·m2；2为驱动连杆的质量，kg；2为驱动连杆的转动惯量，kg·m2；3为轨轮总质量和，kg；3为轨轮的转动惯量，kg·m2；4为链轮1的转动惯量，kg·m2。

2.3 机构势能分析

该铁路扣件回收机构的势能为导向轮的势能、驱动连杆的势能、动平台的势能、轨轮势能之和,以=0为零势能面，滚筒质心正位于零势面，取导向轮的轴坐标1，驱动连杆质心的轴坐标2，动平台质心的轴坐标0，轨轮的质心的轴坐 标3。

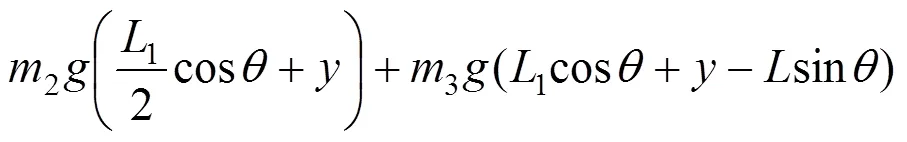
式中：为导向槽宽，m；为导向轮半径，m；1为驱动连杆长，m；为动平台长，m。

2.4 动力学模型的建立

采用拉格朗日方法求解机构上的各个广义分力，该扣件回收机构系统的拉格朗日函数为：

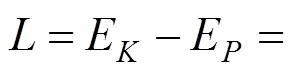
链条牵引机构复位提升时，主要表现为机构的重力势能的提升，并且机构中各构件运动接触均为滚动方式,暂不考虑摩擦因素的阻尼影响。然后根据拉格朗日方程可以得到机构的动力学方程组：

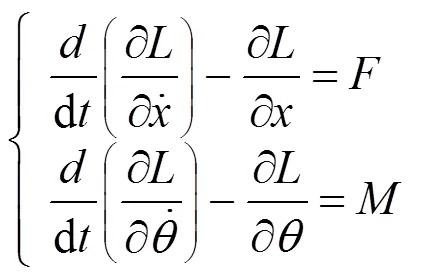
综合上式可以得到：

这样就完成了机构Lagrange动力学方程的建立，式(15)为方程的显示解。当给定机构的运动参数时，通过式(15)可得到等效驱动连杆的驱动力以及驱动力矩，从而可以对机构进行动态特性分析。

3 动力学特性仿真研究

依据文献2中所提及的长钢轨扣件收集装置，设定图3中机构结构参数。转动惯量0=1.09 kg·m2，1=0.089 kg·m2，2=3 633 kg·m2，3=4.98 kg·m2，4=0.28 kg·m2，质量为0=360 kg，1=28 kg，2=21 kg，3=249 kg，4=29 kg，机构的其他结构尺寸如表2所示。

为了分析机构的结构参数对驱动力及驱动力矩的影响规律，结合图3所示的机构位置姿态图，采用Matlab软件对上述计算公式进行计算机仿真，暂且不考虑动平台上扣件负载的施加。设定电机在恒转速条件下，链条驱使动平台复位提升，将动平台的复位过程可视为动平台水平匀速运动与绕滚筒做渐开线形式运动的叠加，因而动平台质心的运动轨迹参数方程为：

表2 扣件回收装置结构尺寸

在上述给定条件下，通过仿真计算，得到机构复位过程的4个阶段的动力参数曲线，机构等效驱动连杆输出的驱动力仿真曲线如图4所示，驱动转矩仿真曲线如图5所示。运动阶段Ⅰ时间范围为0~6 s，在滚筒的约束下，随着机构沿长钢轨面移动，驱动力缓慢增大，驱动转矩逐渐减小，具体表现为该阶段链条牵引机构沿钢轨面移动，整体结构重心上移，动平台与钢轨面之间的倾斜角度变大，作用于滚轮中心的力臂减小，整体重力矩减小，相应驱动转矩减小。运动阶段Ⅱ处于6~58 s内，驱动力平缓增大，驱动转矩显著减小，该阶段导向轮接触导向槽上沿，随着机构整体右移，滚轮脱离钢轨面，此时为平衡机构重力矩的增大，驱动转矩突变至最大值，之后机构位于滚筒转动中心右侧部分的重力矩逐渐变大，而其左侧部分的重力矩则逐渐变小，整体机构的重力矩逐渐减小，因而驱动转矩也将逐渐减小。运动阶段Ⅲ处于58~63 s内，驱动力逐渐增大至最大值，驱动转矩反向增大，该阶段中导向轮脱离导向槽上沿，逐渐落于导向槽下沿，并将加速运动产生很大的冲击。为避免产生冲击，保证机构运动平稳，因而电机会产生反向制动转矩，等效于向驱动连杆提供反向转矩。运动阶段Ⅳ处于63~73 s内,该阶段导向轮落于导向槽下沿，整体机构的重心趋于稳定，驱动力逐渐减小，驱动转矩突变为正向，并逐渐减小。

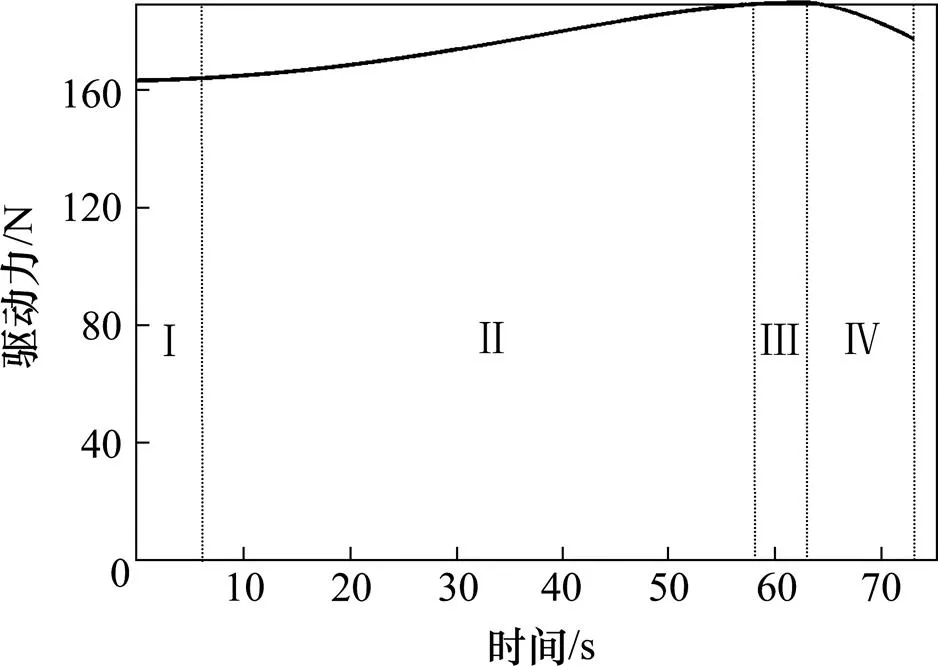
图4 驱动力的变化曲线

图5 驱动转矩的变化曲线

在工程实际中，依据图2所示机构复位动作阶段，结合图4中复位运动的4个阶段中驱动力的变化趋势，运动阶段Ⅰ，Ⅱ和Ⅲ中，动平台复位提升过程中驱动力缓慢增长，与实际作业中收料机构复位动作逐渐增快的运动特性相符。在复位过程的Ⅲ和Ⅳ阶段，由于机构重心右移，在机构重力矩的作用下，驱动源勿需提供过多的动力，并通过减少导向槽宽的值来避免冲击。

根据上述机构复位过程中各阶段的运动特性分析，结合图5中驱动转矩的变化趋势，在由阶段Ⅰ至Ⅱ时，电机恒转速输出，带动链条驱使滚轮脱离长钢轨面，此时机构左端悬空(如图3所示)，为平衡机构整体重力矩的变化，电机的输出转矩必然增加，以满足此时机构动作所需驱动转矩的突变要求。此时电机的功耗可以给电机额定功率的选取提供直接参考，为避免驱动电机超载运行，可以在运动阶段Ⅰ末端位置设置限位并控制电机在更低速度下运行。在阶段Ⅱ至Ⅲ时，动平台在滚筒支撑下，其右边的重力矩大于左边，由于机构重心右移，在机构重力矩的作用下，使电机处于负负载运行，为避免电机超速，可在阶段Ⅲ设置限位并使电机短时制动。在阶段Ⅲ至Ⅳ时，导向轮接触导向槽下沿，机构重心趋于稳定，无需电机再提供反向制动转矩维持机构运转的平稳，此时所需的驱动转矩较小，可以适当设置限位并控制电机以较高的速度运行。针对所需驱动转矩的三次突变，对于电机的容量及控制需提出更高的速度控制要求。实际上，我们用功率3 kW的三相异步交流电机作驱动源(额定转速1 430 r/min，最大输出扭矩为20 N·m)，采用变频调速的方法，驱动减速比为=80的减速器，再由减速器通过链条驱动机构运动，满足所需最大驱动转矩1 400 N·m的驱动要求。

结合整个运动阶段中机构运动规律分析表明，驱动转矩的变化与机构的重力矩的变化趋势对应相符，仿真运动特性满足实际作业时的安全性及稳定性，同时也最大程度保证整体机构复位动作的时效性要求。

为了探究在一定牵引功率下等效驱动连杆最佳的动力输出，需要分析机构结构参数对于动平台复位动作的动力影响。本文中链条带动连杆，作用给连杆构件的牵引力效果可分为驱动力矩和驱动力，结合图2中运动阶段Ⅰ姿态角度变化规律可知，导向槽宽与连杆沿竖直方向倾角的范围极值成线性关系，因而导向槽宽度与等效驱动连杆的动力输出有直接关系。首先保证结构复位提升动作的顺利完成，同时考虑到到铁路线上的安全限高2.6 m，从而确定导向槽的宽度范围。分析导向槽宽度对于运动阶段Ⅱ动平台达到的最大高度的影响，结合机构运动阶段Ⅰ中运动规律的几何关系=sin，=sin−(+)−cos(sin−−)/cos(取= 20°)，其影响关系如图6所示。可以看出导向槽宽度与最大高度成线性对应关系。由此可知在，导向槽宽与倾角也成线性对应关系。为保证机构动平台的复位提升动作无干涉，因而槽宽应不小于2倍的导向轮直径即＞4，其次保证动平台所达到的最大高度不超过铁路安全高度，可知导向槽宽度介于200~400 mm。

图6 导向槽宽度对最大高度值的影响

该机构导向槽宽参数对驱动力及驱动力矩的影响分别如图7和8所示。由导向槽宽与运动阶段Ⅱ中的起始倾斜角的线性对应关系，结合图7和8可知在一定范围内导向槽宽对驱动力、驱动力矩的影响规律：增大导向槽宽，有利于增大等效驱动力及驱动转矩。然而考虑到运动阶段Ⅲ中导向轮落于导向槽下沿，存在冲击载荷，不利于铁路运输安全，因而导向轮不宜匹配过宽的导向槽，必须保证整体装置复位提升动作安全平缓。

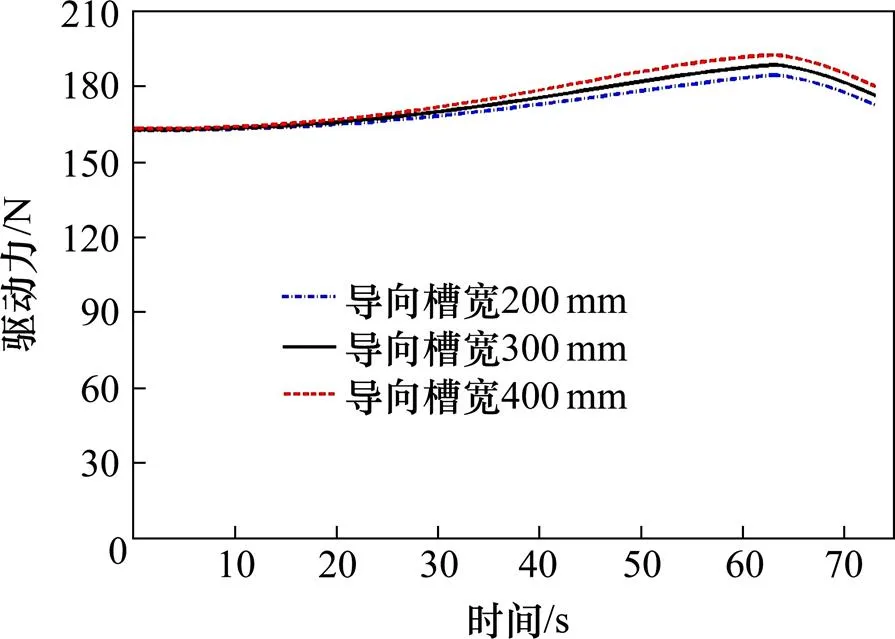
图7 导向槽宽度对驱动力的影响

图8 导向槽宽度对驱动力矩的影响

4 结论

1) 用Lagrange方程对一种长钢轨换轨扣件回收机构进行动力学分析，得到了机构驱动力、驱动转矩的显示解，采用Matlab对机构动力学仿真，得到的动力变化曲线满足实际工况要求，并且分析了不同结构下驱动力、驱动转矩的变化差异，对机构结构优化设计提供了参考。

2) 长钢轨换轨扣件回收机构延伸下放作业是复位提升作业的逆向动作，分析可知机构延伸下放过程中机构反向驱动力与反向驱动转矩，分别为图4和5中驱动力与驱动转矩曲线的逆向，这对于驱动电机的选型具有重要的参考价值。

3) 根据该长钢轨扣件回收机构的动力分析结果，研制的工务钢轨扣件回收装置，目前已在淮南、京沪、新长等线路大修换轨施工中，已安全试运行200 km以上，且运行快捷稳定，实践证明该分析模型及结论可为类似机构的动力学特性的深入分析和机构优化设计提供了理论依据。

[1] 卢祖文. 我国铁路的钢轨扣件[J]. 中国铁路, 2005(7): 25−27, 10. LU Zuwen. Rail fastener of China railways[J]. China Railway, 2005(7): 25−27, 10.

[2] 陈水胜, 吴博, 孔加超, 等. 一种长钢轨换轨扣件收集装置:中国: CN106743782A[P]. 2017−05−31. CHEN Shuisheng, WU Bo, KONG Jiachao, et al. A long rail fastener collection device: China: CN106743782A[P]. 2017−05−31.

[3] 陈树勋, 应鸿烈, 王海波. 拉臂式压缩垃圾车车厢结构的载荷表达与优化设计[J]. 机械设计, 2010, 27(3): 62−67. CHEN Shuxun, YING Honglie, WANG Haibo. Load expression and optimization of compartment structure of hook-lift compressed rubbish truck[J]. Journal of Machine Design, 2010, 27(3): 62−67.

[4] 武力, 关天民, 张雪涛, 等. 垃圾转运车翻转车架结构优化设计[J]. 机械设计, 2013, 30(5): 41−44. WU Li, GUAN Tianmin, ZHANG Xuetao, et al. Structure optimization design of turning frame of garbage transfer vehicle[J]. Journal of Machine Design, 2013, 30(5): 41−44.

[5] Takanos, Nagai Taniguchi T. Study on a vehical dynamics model for improving roll stability[J]. JSAE Review, 2003, 24(6): 149−156.

[6] Slavic J, Boltezar M. Simulating multibody dynamics with rough contact surfaces and run-in wear[J]. Nonlinear Dynamics, 2006, 45(12): 353−365.

[7] 宁永芳, 高广军. 矿用载人快速轨道车设计及动力学分析[J]. 铁道科学与工程学报, 2014,11(2): 121−124. NING Yongfang, GAO Guangjun. Structure design and dynamic analysis of passenger car[J]. Journal of Railway Science and Engineering, 2014, 11(2): 121−124.

[8] 丁华锋, 刘征, 刘帅, 等. 一种新型正铲液压挖掘装置的运动学和动力学分析[J]. 机械工程学报, 2015, 51(1): 60−68. DING Huafeng, LIU Zheng, LIU Shuai, et al. Kinematics and dynamics analysis of an innovative face-shovel hydraulic excavator in mining[J]. Journal of Mechanical Engineering, 2015, 51(1): 60−68.

[9] 陈亚, 尤伟, 章易程, 等. 生命探测履带车过沟性能的仿真分析[J]. 铁道科学与工程学报, 2016, 13(10): 2051 −2055. CHEN Ya, YOU Wei, ZHANG Yichen, et al. Simulation and analysis of pit-crossing performance of life detection tracked vehicle[J]. Journal of Railway Science and Engineering, 2016, 13(10): 2051−2055.

[10] 张军, 谢志江. 基于Lagrange方程的3-PPR并联机构动力学分析与仿真[J]. 组合机床与自动化加工技术, 2016, 18(8): 57−60. ZHANG Jun, XIE Zhijiang. Dynamics analysis and simulation of 3-PPR parallel mechanism based on Lagrange[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016, 18(8): 57−60.

[11] ZHAI W M. Two simple fast integration methods for large scale dynamic problem in engineering[J]. International Journal for Numerical Methods in Engineering, 1996, 39(24): 199−214.

[12] CHEN Shuxun, YE Shanghui. A guide-weight criterion method for the optimal design of an tenna structures[J]. Engineering Optimization, 1986, 10(3): 199−216.

[13] 沈惠川, 李书民. 经典力学[M]. 合肥: 中国科学技术大学出版社, 2006: 95−130. SHEN Huichuan, LI Shumin. Classical mechanics[M]. Hefei: University of Science and Technology of China Press, 2006: 95−130.

[14] Zienkiewicz O C, Campbell J S. Shape optimization and sequencial linear program[J]. Optimization Structural Design London: John Wiley & Sons, 2005, 12(5): 216− 221.

[15] 宋志安, 张鑫, 宋玉凤, 等. MATLAB/Simulink机电系统建模与仿真[M]. 北京: 国防工业出 版社, 2015: 74− 79. SONG Zhian, ZHANG Xin, SONG Yufeng, et al. Modeling and simulation of electromechanical system based on MATLAB/Simulink[M]. Beijing: National Defense Industry Press, 2015: 74−79.

(编辑 蒋学东)

Dynamics analysis of long railway fastener recovery mechanism based on Lagrange’s equation

CHEN Shuisheng1, WU Bo1, YAN Jianming2, HU Weiming2

(1. School of Mechanical Engineering, Hubei University of Technology, Wuhan 430068, China; 2. Shanghai Railway Administration, Shanghai Major Repair Work Section of Railway, Shanghai 200040, China)

By analyzing the change of potential energy in the movement process, combining the relations between the mechanism structure and drive parameters, the driving parameters were given based on Lagrange’s equation, for the study of the drive characteristics of a long rail fastener recovery mechanism. With the kinematics characteristics of the mechanism, dynamic simulation analyses by Matlab were performed to investigate the dynamics characteristic curves. To further study the optimal power output of equivalent drive linkage under certain tractive power, the differentials of driving force and driving torque with different structures were analyzed, and the interaction laws of the influence of changing structures on the effect of dynamics were obtained. The results prove the dynamic curves by simulation are close to the actual working condition. Therefore, the results provide references for detailed research on dynamic characteristic and optimal design of the similar mechanism.

mechanism; drive; Lagrange’s equation; dynamic characteristics; structure optimization

10.19713/j.cnki.43−1423/u.2018.10.030

U215.6

A

1672 − 7029(2018)10 − 2677 − 08

2017−10−13

上海铁路局基金资助项目(2016083)

陈水胜(1969−)，男，湖北武汉人，副教授，从事机械设计制造及其自动化研究；E−mail：cssg@163.com