时速250 km/h铁路双线箱梁的扭转效应研究

马俊军，蔺鹏臻



时速250 km/h铁路双线箱梁的扭转效应研究

马俊军1，蔺鹏臻2

(1. 兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070； 2. 兰州交通大学 土木工程学院，甘肃 兰州 730070)

为了准确分析时速250 km/h客运专线32 m标准双线简支箱梁的约束扭转效应，基于箱梁约束扭转时截面变形和约束扭转微分方程，建立能够准确模拟实际边界条件的有限元数值模型。分别采用有限元法和解析法，对比分析仅在单线活载作用下箱梁约束扭转翘曲应力的大小以及变化规律。通过定义扭转翘曲系数，研究结构设计参数高跨比、高宽比和宽厚比对箱梁约束约束扭转的影响。研究结果表明：按本文方式建立的有限元方法能够有效地模拟箱梁约束扭转效应；在单线活载作用下，跨中截面翘曲系数很大，顶板与腹板交点处翘曲系数为8.94%，悬臂板端部翘曲系数最大，可达10.24%，而1/4截面翘曲系数却很小，几乎接近于0；箱梁的结构设计参数对箱梁约束扭转效应均有一定影响，总体规律是双线铁路箱梁约束扭转效应随着高跨比、高宽比和厚高比的增加而增大。

双线铁路；箱梁；约束扭转；翘曲应力；有限元分析

与高速公路桥梁相比，高速铁路具有速度高、活荷载大和线路要求高等特点，往往要求其桥跨结构具有更大的抗弯和抗扭刚度。与其他截面形式相比，箱形截面具有抗弯刚度大、抗扭刚度大、结构自重轻和外形美观等优点，因此，在国内外高速铁路桥梁建设中一直被广泛采用[1]。但是箱梁在不对称荷载作用下，除了发生纵向弯曲外，还会发生扭转和畸变，从而使截面产生一定的翘曲应力。对于双线高速铁路桥而言，当仅有单线列车运行时，列车活载相当于作用在箱梁纵向的竖向偏心荷载，将引起桥梁很大程度的扭转和畸变[2−3]。因此，在双线高速铁路设计时应充分考虑箱梁约束扭转的影响。对于箱梁约束扭转分析，目前，国内外采用的分析方法主要有解析法[4, 6]和有限元法[7−11]。解析法主要是基于梁理论的一维分析方法，主要是采用初参数法，通过已知的刚性扭转荷载和边界条件来求解箱梁约束扭转控制微分方程，从而获得截面约束扭转翘曲应力。由于约束扭转微分方程是高次微分方程，往往在求解时比较繁琐，不容易求解。有限元法是把组成箱梁的各个板件离散成为三维的壳体和块体，从而建立计算精度高、适用性强的三维有限元精细化模型，能够比较真实地模拟箱梁在荷载作用下的空间受力特性，求解速度快、精度高、求解过程简便，但是对于边界条件的处理往往比较复杂。本文以时速250 km/h客运专线32 m标准跨度双线简支箱梁为研究对象，通过采用板壳单元有限元数值模拟来研究箱梁在单线活荷载作用下的约束扭转效应，并和传统理论解进行对比分析。同时研究在单线活荷载作用下双线铁路箱梁的结构参数对箱梁约束扭转的影响。

1 约束扭转效应分析模型

1.1 箱梁的基本参数

以时速250 km/h客运专线32 m标准跨度双线简支箱梁为例，跨中截面如图1所示。桥梁设计标准为双线，线间距为4.6 m。轨道结构采用双块式无砟轨道，桥面板上直接铺设无砟轨道底座板。列车活荷载纵向采用标准活荷载。梁体采用C50混凝土，弹性模量按规范[13]取值为=3.55×104MPa，材料泊松比按规范取值为=0.2。

单位：m

1.2 荷载施加

当双线铁路桥上只有单线列车运行时，整个列车活荷载相当于作用在桥上的偏心荷载，扭转会使得桥梁产生一定的约束扭转翘曲应力。因此对双线铁路桥梁在单线列车行驶时的约束扭转效应分析是很有必要的。根据现有的铁路桥梁设计规范[14]，列车荷载采用标准活载，其冲击系数取为1.08，荷载布置如图2所示。

图2 加载示意图

对图3(a)所示的承受偏心外荷载的箱梁，根据静力平衡条件[6]，如图3(b)所示可将偏心荷载向箱梁中心平移，进一步经过图3(c)~3(f)分解后，获得了最基本的弯曲荷载模式如图3(d)，刚性扭曲荷载模式如图3(e)，畸变荷载模式如图3(f)。

根据图3可以计算得到图2所示荷载作用下箱梁约束扭转荷载分别为：

图3 偏心荷载的分解

1.3 有限元模型

本文将组成箱梁的各个构件离散成板，利用ANSYS有限元分析shell63板壳单元建立混凝土箱梁的实体模型。主要分析箱梁在刚性扭转荷载作用下箱梁各个截面翘曲应力的变化规律。将上述扭转荷载分别平均作用在箱梁对应截面的各个结点上，建立有限元分析模型，建立的模型如图4所示。

(a) 横截面；(b) 空间透视

1.4 边界条件

箱梁约束扭转分析时，力学模型和有限元模型的等效是非常有必要的。因此，不仅仅要对结构的受力进行等效外，还应对边界条件也进行等效。

基于一维梁理论的箱梁约束扭转的基本方 程[6]为：

式中：为材料弹性模量；I为广义扇形静矩；为截面扭转角；为材料的剪切模量；为截面约束系数；I为截面抗扭惯性矩；为约束扭转荷载。

对应的边界条件为：

1) 简支梁：

=0；σ=0 (5)

式中：为截面扭转角；σ为约束扭转翘曲正应力。

2) 固定端：

=0；′=0 (6)

式中：含义同上；′为广义翘曲，反应翘曲程度。

3) 悬臂梁：

式中：σ含义同上；为计算参数，具体参照文 献[6]。

由前述分析可知，约束扭转是箱梁在偏心运营荷载下组合受力模式之一，在一维梁的解析法中可容易确定约束扭转效应的边界条件。但对于空间板壳单元有限元模型，必须基于约束扭转的传力机理，确定处于边界处的结点约束条件。

结合式(4)~(5)，简支箱梁约束扭转时梁端部扭转角(=0)和翘曲正应力(=0)，即箱梁在横截面内不发生位移，只有沿桥梁纵向发生位移。因此，对于图5所示箱梁端部结点布置，符合式(5)的边界约束如表1所示。

图5 结点示意图

表1 结点约束信息

注：1表示相应的位移受到约束，0表示不受约束

2 双线铁路箱梁约束扭转翘曲应力对比

2.1 双线铁路箱梁跨中截面约束扭转效应分析

对上述建立的有限元模型，施加按照图2所示的刚性扭转荷载，求解得到双线铁路箱梁在单线列车活载下的约束扭转翘曲应力。同时，采用基于式(4)的一维梁理论计算箱梁在约束扭转作用下的翘曲正应力，与采用shell63板壳单元的有限元结果进行对比，对比结果如图6所示。

从图6可以看出，按照shell63单元计算的有限元解和按照一维梁理论计算的理论解的分布规律一致，但传统的理论解由于公式推导中简化较多，计算结果偏大，最大相差发生在底板与腹板交接处，最大相对误差为41%。说明按照本文方式建立的有限元方法可以更好地模拟箱梁的约束扭转 效应。

单位：kPa

注：括号中的为有限元解

应力计算结果表明，双线铁路箱梁在单线列车活荷载作用下，跨中悬臂板端部的翘曲应力值比截面其他部位的应力值要大，说明双线铁路桥梁在单线列车行驶的情况下，箱梁跨中截面悬臂板端部扭转翘曲正应力最突出。

2.2 双线铁路箱梁跨中截面约束扭转翘曲应力分析

为了能够更好地反应双线铁路箱梁在单线列车活荷载作用下的约束扭转效应，引入约束扭转翘曲系数反应箱梁约束扭转翘曲程度，其表达 式为：

式中：σ为约束扭转翘曲应力；为截面的纵向弯曲应力。约束扭转翘曲系数反应双线铁路箱梁在单线列车活载作用下约束扭转翘曲应力占弯曲应力的百分比。

为了能够反应箱梁在活荷载作用下的翘曲程度，本文将跨中截面顶板、底板和悬臂板部分分成10份，分别计算截面各个部分约束扭转翘曲系数，结果如图7所示。通过跨中截面各个部分的翘曲系数可以反映截面在活载作用下翘曲正应力在跨中截面的翘曲程度，反应跨中截面翘曲程度的变化规律。

图7 跨中截面翘曲比例系数ξ

从图7计算的翘曲系数可以看出，在单线活载作用下，跨中截面顶板及底板的翘曲比例系数离截面中心越远，翘曲比例系数越大，顶板翘曲比例系数远大于底板。跨中截面悬臂板端部翘曲系数数值大于截面其他部位，表明双线铁路箱梁在单线荷载作用下，箱梁悬臂端部翘曲程度最明显，这和2.1中得到的结论一致。除此之外，从数值结果可以看出，在单线活载作用下，跨中截面的顶板、腹板和底板中心处翘曲系数几乎为0；跨中截面悬臂端部扭转翘曲系数最大值为10.24%；顶板与腹板连接处最大翘曲系数为8.94%；底板与腹板连接处最大翘曲系数为3.82%。

3 结构参数对约束扭转效应的影响

3.1 高跨比对约束扭转效应的影响

为了便于描述和分析结构设计参数对双线铁路箱梁约束扭转效应的影响，取截面翘曲应力较大的3个点作为控制点，分别为：

1) 左侧腹板与底板连接处，简记为：底板与腹板交点；

2) 左侧顶板与腹板连接处，简记为：顶板与腹板交点；

3) 右侧悬臂板端部，简记为：悬臂端点。

高跨比(/)是桥梁结构设计的重要参数。为了更好地反映双线高速铁路在单线偏心列车活载作用下截面约束扭转翘曲应力的变化规律，本文在图1所示的客运专线32 m标准跨度双线简支箱梁的基础上，通过改变桥梁跨度来实现高跨比的改变。不同的高跨比下，跨中截面和1/4截面处的约束扭转翘曲系数分别如图8(a)和8(b)所示。

(a) 跨中截面；(b) 1/4截面

从图8(a)可以看出，随着结构设计参数高跨比的增加，跨中截面底板与腹板交点、顶板与腹板交点和悬臂端部处的翘曲系数逐渐增加。悬臂端部的翘曲系数明显大于底板与腹板交点以及顶板与腹板交点处的翘曲系数。除此之外，悬臂端部曲线的斜率随着高跨比的增加逐渐增加，这说明跨中截面悬臂端部纵向翘曲应力所占的比例同样也是逐渐增大的，而且变化的幅值是单调递增的。

从图8(b)可以看出，1/4截面上3点处的翘曲系数的变化规律和跨中一致，也是随着高跨比的增加，各个点的翘曲系数也是逐渐增加的。不同的是，在高跨比较小时，各个点翘曲系数数值接近0，主要是由于简支梁在集中荷载作用处，截面翘曲双力矩虽然非常大，但衰减很快，在1/4截面处，翘曲双力矩几乎为0，意味着翘曲正应力非常小，表明1/4截面产生的约束扭转翘曲应力所占比例非常小。

综上所述，本文研究的时速250 km/h客运专线32 m标准跨度双线箱梁的高跨比为0.079 7，翘曲程度最为明显的跨中截面底板与腹板交点、顶板与腹板交点和悬臂端部所对应的翘曲系数为3.82%，8.94%和10.24%。

3.2 宽高比

同高跨比一样，桥梁结构设计参数宽高比(/)，也对箱梁约束扭转有一定的影响。为了研究不同的宽高比对箱梁约束扭转的变化规律，在图1所示的箱梁截面的基础上，通过改变截面的高度来实现截面宽高比的变化。计算跨径取为24和32 m，分别研究不同截面高度下跨中截面各个控制点约束扭转翘曲系数的变化规律，结果如图9所示。

(a) 计算跨径24 m；(b) 计算跨径32 m

图9揭示了不同跨径下跨中截面各个控制点在不同宽高比下的翘曲系数的变化规律。从曲线数值的变化来看，悬臂端部的翘曲系数随着宽高比的增加而逐渐减小，底板与腹板交点、顶板与腹板交点处翘曲系数随着宽高比的增大而增大，但增加值不到5%。从曲线的斜率来看，悬臂端部翘曲系数变化曲线的斜率随着宽高比的增加逐渐减小，而底板与腹板交点、顶板与腹板交点翘曲系数变化曲线的斜率基本保持不变，表明双线铁路箱梁在单线列车活载作用下，跨中截面约束扭转效应最明显的部位是悬臂板部分。

图9(a)和9(b)对比可知，跨径为32 m时截面各个控制点的翘曲系数数值明显小于跨径24 m时的翘曲系数，表明随着跨度的减小，箱梁约束扭转的效应变的更加明显，这和3.1中得到结论相一致。

除此之外，从图中数据可以看出，底板与腹板交点和顶板与腹板交点的翘曲系数数值明显小于悬臂端部的翘曲系数，故随着截面宽高比的增加，箱梁约束扭转翘曲系数总体上是逐渐减小的，说明采用较小高度的箱梁有助于抑制箱梁约束扭转 效应。

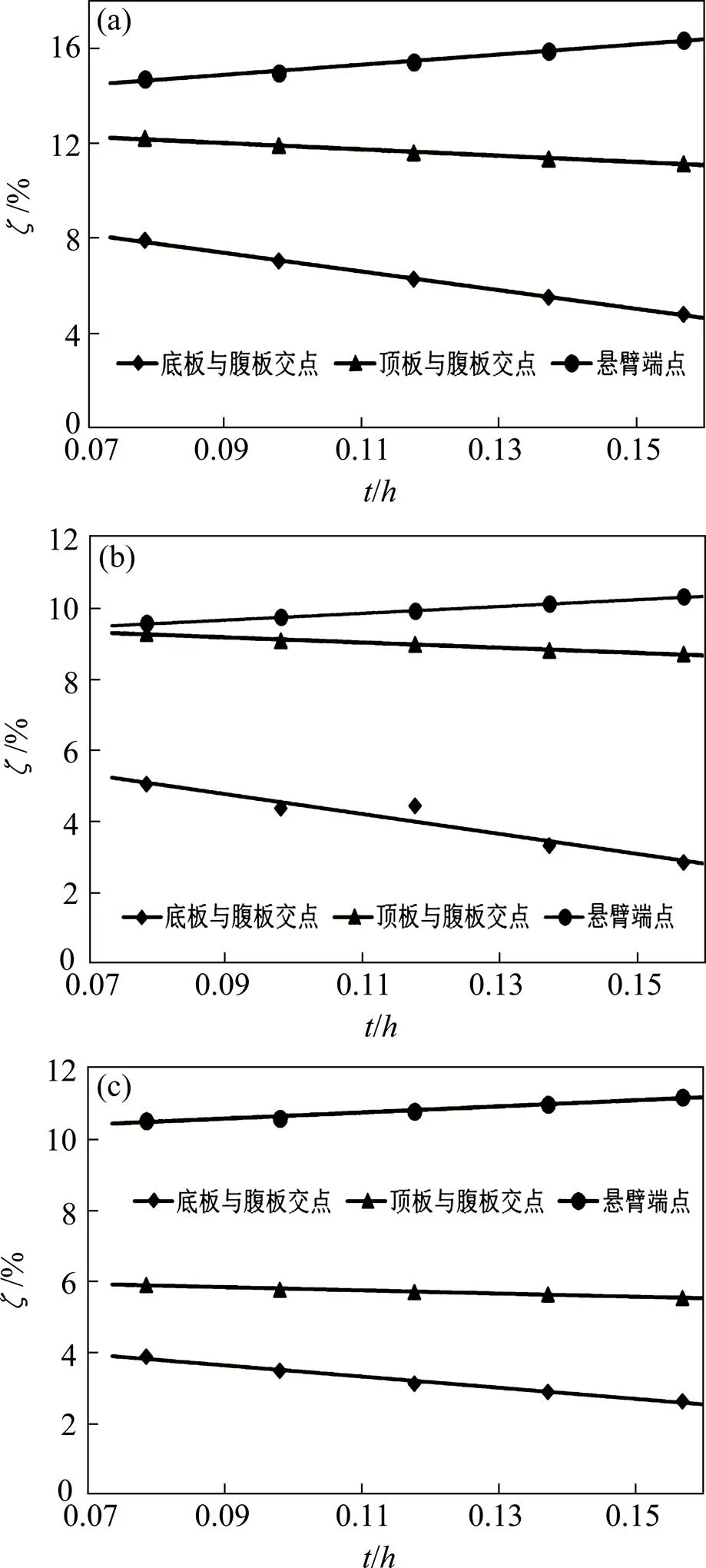
3.3 厚高比

在高跨比和宽高比的基础上，还研究了厚高比(/)对双线铁路箱梁约束扭转翘曲系数的影响。因为箱梁纵向应力最大部位位于截面的顶板和底板，故本文只通过改变箱梁顶板和底板的厚度来实现截面厚高比的变化。计算跨径分别取为24，32和40 m，研究不同跨径下跨中截面各个控制点翘曲系数随厚高比的变化规律，计算结果如图10所示。

图10揭示了不同跨度下，跨中截面各个控制点翘曲系数随参数厚高比的变化规律。悬臂端部翘曲系数随着厚高比的增加而增加，底板与腹板交点、顶板与腹板交点随参数厚高比的增加而减小。

从图10(a)，10(b)和10(c)的对比来看，结构在任意厚高比下，跨中截面各个控制点的翘曲系数随着跨度的增加而减小。除此之外，从曲线的斜率来看，随着跨度的增加，各控制点翘曲系数随厚高比变化的趋势逐渐减小。

从控制点翘曲系数的数值来看，悬臂端部的翘曲系数数值大于其他控制点的。因此，从总体上来看，随着截面厚高比的增加，双线铁路箱梁约束扭转效应越明显，意味着适当增加顶板和底板的厚度，可以有效地减小箱梁的约束扭转效应。

(a) 计算跨径24 m；(b) 计算跨径32 m；(c) 计算跨径40 m

4 结论

1) 按照本文建立的有限元解与传统解析解相比，翘曲应力的变化趋势相一致，但由于传统解析解是在一维梁理论的基础上建立的，在分析计算中存在很大的简化，计算结果往往偏大。与解析法相比，本文建立的有限元方法能够有效地模拟箱梁的约束扭转效应，能够更加真实地反应箱梁在约束扭转时的空间受力特性。

2) 双线铁路简支箱梁仅在单线最不利活荷载作用下，跨中截面约束扭转翘曲效应最明显，其中截面悬臂板端部、顶板与腹板连接处以及腹板与底板连接处为翘曲应力最大的点。在标准活载作用下，截面悬臂板端部翘曲效应最明显，其翘曲应力占活载弯曲总应力的10.24%。

3) 通过对双线铁路箱梁约束扭转翘曲应力分析，结果表明，在标准活载作用处，约束扭转翘曲系数最大，但衰减很快；远离活载作用处，翘曲系数几乎为0。

4) 客运专线双线铁路桥梁的结构设计参数对箱梁约束扭转效应均有一定的影响，总体规律是双线铁路箱梁约束扭转效应随着高跨比、高宽比和厚高比的增加而增大。

[1] 贾卫华. 武广高速铁路双线整孔简支箱梁预制技术[J]. 铁道科学与工程学报, 2010,17(2): 74−78. JIA Weihua. Prefabricating technology of double line whole-span simply supported box girder in Wuguang high speed railway[J]. Journal of Railway Science and Engineering, 2010, 17(2): 74−78.

[2] 黄剑源. 薄壁结构的扭转分析[M]. 北京: 中国铁道出版社, 1983. HUANG Jianyuan. Torsional analysis of thin-walled structures[M]. Beijing: China Railway Press, 1983.

[3] 项海帆. 高等桥梁结构理论[M]. 2版. 北京: 人民交通出版社, 2013.XIANG Haifan. The higher bridge structure theory[M]. 2nd ed. Beijing: China Communications Press, 2013.

[4] 张元海, 李乔. 考虑剪滞变形及约束扭转二次剪切变形影响时薄壁曲线箱梁的挠曲扭转分析[J]. 土木工程学报, 2009, 42(3): 93−98. ZHANG Yuanhai, LI Qiao. Flexural-torsional analysis of thin-walled curved box girders with shear lag and secondary shear deformation in restraint torsion[J]. China Civil Engineering Journal, 2009, 42(3): 93−98.

[5] 徐勋, 叶华文, 强士中. 带悬臂板薄壁箱梁的扭转和畸变分析[J]. 铁道学报, 2015, 37(10): 860−866. XU Xun, YE Huawen, QIANG Shizhong. Torsion and distortion analasis of thin-walked bok girder with cantilever flangers[J]. Journal of the China Railway Society, 2015, 37(10): 860−866.

[6] 郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 2版. 北京: 人民交通出版社, 2008. GUO Jinqiong, FANG Zhenzheng, ZHENG Zhen. Design theory of box girder[M]. 2nd ed. Beijing: China Communications Press, 2008.

[7] 聂国隽, 钱若军. 考虑约束扭转的薄壁梁单元刚度矩阵[J]. 计算结构力学及其应用, 2002, 19(3): 344−348. NIE Guojun, QIAN Ruojun. Element stiffness matrix of thin-walled beam considering restrained torsion[J]. Chinese Journal of Computational Mechanics, 2002, 19(3): 344−348.

[8] 金声, 李开禧, 熊晓莉. 开口薄壁构件弯扭屈曲的单肢解析化分析方法[J]. 工程力学, 2009, 26(6): 16−20. JIN Sheng, LI Kaixi, XIONG Xiaoli. Slabs-disassembled method of flexural-torsional bucking of thin-walled open-profile members[J]. Engineering Mechanics, 2009, 26(6): 16−20.

[9] 王晓峰, 杨庆山. 考虑横向和扭转剪切变形的空间薄壁梁单元[J]. 力学学报, 2013, 45(2): 293−296. WANG Xiaofeng, YANG Qingshan. A new spatial thin-walled beam element including transverse and torsional shear deformation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2): 293− 296.

[10] 卢彭真, 魏召兰, 占玉林, 等. 基于位移场的薄壁箱梁结构约束扭转和畸变效应分析[J]. 四川大学学报(工程科学版), 2009, 41(1): 74−79. LU Pengzhen, WEI Zhaolan, ZHAN Yulin, et al. Analysis of restrained torsion and distortion effect for thin-walled box girder structure based on displacement field[J]. Journal of Sichuan University (Engineering Science Edition), 2009, 41(1): 74−79.

[11] 王增荣, 李之榕, 李仰训. 箱梁扭转畸变的分析[J]. 铁道学报, 1985, 7(4): 87−98. WANG Zengrong, LI Zhirong, LI Yangxun. Analysis on torsion and distortion of box girders[J]. Journal of the China Railway Society, 1985, 7(4): 87−98.

[12] 蔺鹏臻, 孙理想, 冀伟, 等. 时速 250 km /h 铁路双线箱梁的畸变效应研究[J]. 铁道科学与工程学报, 2016, 13(4): 595−599. LIN Pengzhen, SUN Lixiang, JI Wei, et al. Distortion effect of double track railway box girders with speed of 250 km/h[J]. Journal of Railway Science and Engineering, 2016, 13(4): 595−599.

[13] TB10002.3—2005, 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S]. TB10002.3—2005, Code for design on reinforced and prestressed concrete structure of railway bridge and culvert[S].

[14] TB 10020—2009, 高速铁路设计规范(试行)[S]. TB 10020—2009, Code for design of high speed railway [S].

(编辑 阳丽霞)

Restrained torsion effect of double track railway box girders with speed of 250 km/h

MA Junjun1, LIN Pengzhen2

(1. Key Laboratory of Road & Bridge and Underground Engineering of Gansu Province, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

In order to calculate the restrained torsion effect of double track railway box girders with speed of 250 km/h, a finite element model that simulates the actual boundary conditions is established based on the differential equations and sectional deformation of restrained torsion of box girder. Using finite element method and the traditional analytical method, restrained torsion stress is calculated and analyzed only under single-track live load. By defining parameters of warping ratio, the rules of warping stress influenced by the design parameters of high span ratio, width high ratio and thickness to height ratio are analyzed. The results show that the finite element method can effectively simulate the restrained torsion effect of box girder. Under eccentric live load of single track, the cross section has a great warping ratio, the value of warping ratio on flange edge of top plate is 8.94%, the value of warping ratio on end of cantilever plate is 10.24%, while the warping ratio on section of 1/4 is nearly 0. The design parameters of high span ratio, width span ratio and wall thickness can all influence the restrained torsion effect of box girder. The general rule is that the torsion effect of box girder is increased with the increase of high span ratio, high width ratio and high thickness ratio.

double track railway; box girder; restrained torsion; warping stress; finite element analysis

10.19713/j.cnki.43−1423/u.2018.10.002

U441+.5

A

1672 − 7029(2018)10 − 2463 − 08

2017−08−29

国家自然科学基金重大资助项目(11790281)；国家自然科学基金资助项目(51878323)；中国铁路总公司科技研究开发计划项目(2017G010-C)

蔺鹏臻(1977−)，男，甘肃甘谷人，教授，博士，从事桥梁设计理论研究；E−mail：pzhlin@mail.lzjtu.cn