路基不均匀沉降对车辆-CRTSⅢ型轨道系统动力特性影响

唐进锋，刘文峰，王浩，秦志

路基不均匀沉降对车辆-CRTSⅢ型轨道系统动力特性影响

唐进锋，刘文峰，王浩，秦志

(中南大学 土木工程学院，湖南 长沙 410075)

为研究路基不均匀沉降对车辆—CRTSⅢ型板式轨道系统动力特性的影响，以多体动力学和有限元方法分别计算车辆和轨道系统的动力响应，2个子系统通过轮轨关系实现耦合。建立考虑重力作用的车辆—CRTS Ⅲ型板式轨道空间耦合动力分析模型，利用该模型研究不同行车速度、路基不均匀沉降幅值和波长对系统动力响应的影响。研究结果表明：系统动力响应随行车速度和路基不均匀沉降幅值增加而相应增加，影响行车的路基不均匀沉降幅值限值应由舒适度指标控制，数值应控制在20 mm/20 m以下；系统的动力响应随路基不均匀沉降波长的增加呈先增大后减小的趋势，制定路基不均匀沉降标准时，应将沉降波长与幅值进行综合考虑。

CRTS III板式轨道；路基不均匀沉降；联合仿真；动力响应

CRTS Ⅲ型板式无砟轨道[1]是国家为适应中国高铁“走出去”战略而自主研发的轨道板形式。其继承了CRTS I和CRTS II型板[2]的优点，同时也拥有自己独特的创新点：底座板采用凹槽的限位方式、填充层采用刚度较大的自密实混凝土材料、轨道板结构采用门型钢筋进行优化。路基上铺设板式无砟轨道的核心问题是沉降控制，沉降过大势必使得列车、钢轨、轨道板振动加速度增大，从而造成行车舒适度降低，严重时甚至威胁行车安全性。故研究路基不均匀沉降对车辆和CRTS Ⅲ型板式无砟轨道系统动力特性的影响有重要意义。徐庆元等[3]将动车组考虑为多刚体系统，轨道部分采用三维有限元单元建立，并考虑温度梯度荷载，研究20 m路基不均匀沉降波长下轨道板的应力响应，并提出路基不均匀沉降幅值限值标准；张小会等[4]推导板式无砟轨道的振动方程，提出用非线性弹簧模拟不均匀沉降的方法，分别对不同沉降幅值和沉降波长进行分析，得出8~10 m为CRTSⅠ型板式轨道的不均匀沉降敏感波长；肖威[5]用有限元方法建立CRTS Ⅲ型板式轨道模型，分别分析沉降幅值和波长对轨道静力学性能的影响，然后用移动荷载模拟轮轨力，探讨路基不均匀沉降波长为20 m、沉降幅值20 mm时，无砟轨道结构的动力学特征；韩义涛等[6]建立车辆—轨道垂向动力模型，考虑路基不均匀沉降完全转化为轨面沉降，研究20 m路基不均匀沉降波长下系统的动力响应，提出考虑车速的路基不均匀沉降幅值限值。以往对CRTS Ⅲ型板式轨道路基不均匀沉降下的系统动力响应研究较少，且现有研究多着眼于某一特定不均匀沉降波长下沉降幅值对系统动力特性影响，对不同沉降波长下系统动力响应研究较少；此外，传统分析方法并未考虑板式轨道在重力作用下产生的跟随性沉降，这与实际情况存在差别，并使计算得到的系统动力响应偏小。在计算方法上，目前研究车辆—轨道耦合振动的方法一般为独立编制耦合振动分析程序，但程序通用性不强，一旦结构形式发生变化，就需要重新建立大量复杂的运动方程，并对程序进行大量修改，而且一般其只考虑了垂向振动，对同时研究车辆蛇形运动和线路横向不平顺引起的横向振动[7]也较为困难。而本文利用多体动力学软件Simpack[9]计算车辆的动力响应，其采用相对坐标系建立运动方程，一旦模型建立，系统的运动方程则自动形成；利用有限元方法分析轨道的动力响应，其运用则已十分便捷。然后以轮轨关系实现2个子系统间的数据交换，从而实现车辆—轨道耦合振动分析。因此，本文在吸收国内外研究成果[3−8]的基础上，利用上述方法建立考虑重力影响的车辆—CRTS Ⅲ板式轨道空间耦合动力学模型，通过算例分析对本模型正确性进行验证，并对不同行车速度、路基不均匀沉降幅值和波长工况下车辆—CRTS Ⅲ板式轨道系统的动力响应进行研究。

1 车辆-CRTS Ⅲ型轨道耦合动力学模型

1.1 车辆动力学模型

以CRH-2型高速动车组作为一多刚体系统[10]建立车辆模型。其按悬挂系统分为：轮对、转向架和车体。轮对与转向架通过一系悬挂连接，车体与转向架通过二系悬挂连接。其中轮对考虑沉浮、横移、摇头和侧滚4个自由度，车体和转向架考虑沉浮、横移、摇头、侧滚和点头5个自由度，故每辆客车共有31个自由度。

1.2 CRTS III型板式无砟轨道动力学模型

CRTS III板式轨道模型采用结构动力分析的子结构方法建立，其中无砟轨道板采用实体单元模拟，钢轨用空间梁单元模拟，扣件用弹簧阻尼单元模拟。由于SIMPACK对弹性体变形的计算是通过数量相对较小的模态坐标进行描述的，故必须缩减轨道有限元模型自由度。因此建立模型时，采用Guyan缩减方法[11]，选择弹性轨道模型中“有动力学特征”的部分，使得其描述模态的节点数较少的同时，保证计算结果的精确性。为准确描述轮轨中的高频振动，需要合理选取轨道的模态阶数。根据文献[13]的研究成果，当钢轨模态阶数≥60时，数值结果已趋于稳定，因此，本文钢轨和板式轨道的模态阶数分别取为60。图1为建立的车辆—CRTS III板式轨道耦合动力学模型。

1.3 轮轨关系

采用SIMPACK轮轨模块建立考虑蠕滑和轮轨分离的轮轨关系，利用赫兹非线性弹簧接触理论计算接触力，Kalker简化理论(FASTSIM)计算蠕滑力。

图1 车辆—CRTS III 型板式轨道耦合动力学模型

1.4 不平顺激励

1.4.1 随机不平顺

我国的无砟轨道高速不平顺谱[12]采用分段幂函数拟合，谱的空间频率为0.005~0.5(1/m)，对应的轨道不平顺波长为2~200 m，各段轨道谱的表达式如式(1)所示：

式中：()为轨道不平顺功率谱密度，mm2/(1/m)；𝑓是空间频率，1/m；和为拟合系数，我国高速铁路无砟轨道不平顺谱拟合系数如表1所示，对应各分段点的空间频率及对应波长如表2所示。

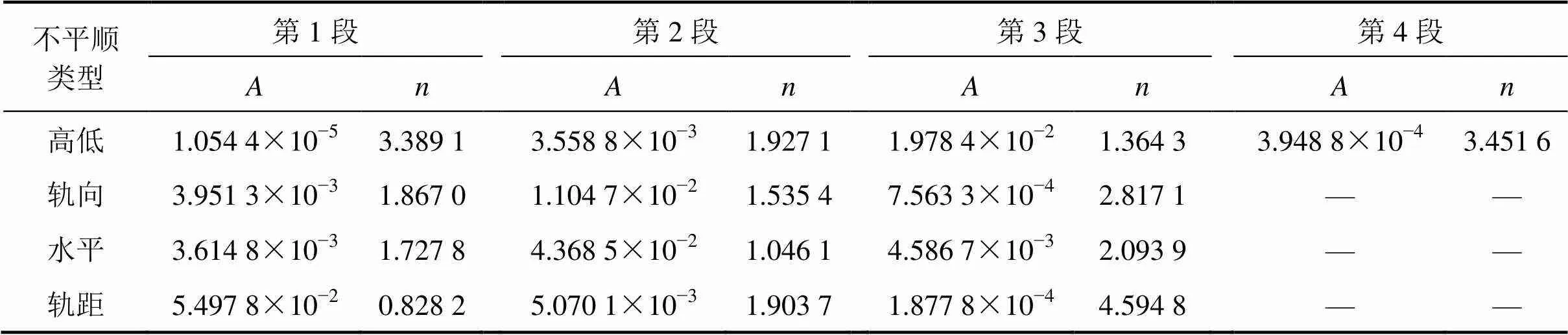
表1 中国高速铁路无砟轨道不平顺谱拟合系数

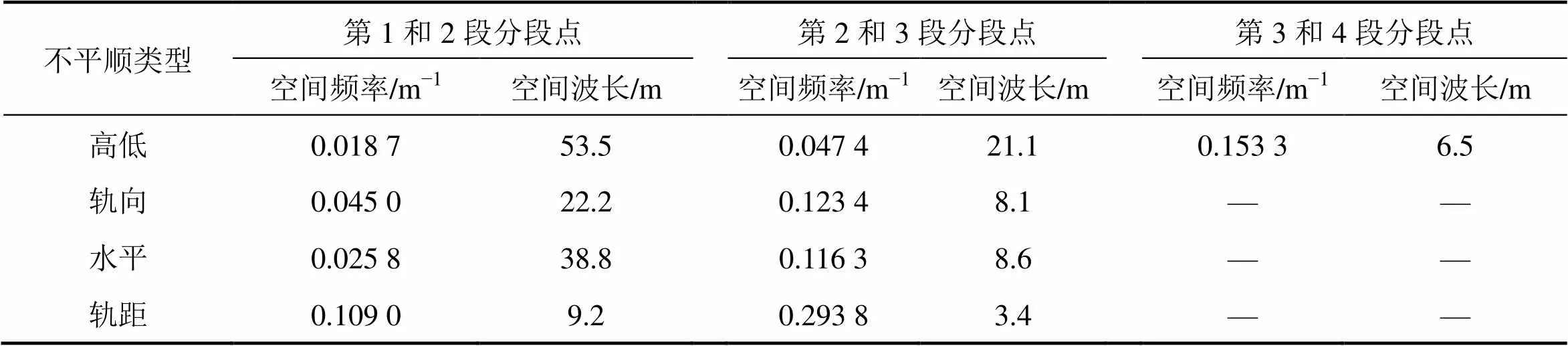
表2 中国高速铁路无砟轨道不平顺谱分段点频率

1.4.2 路基不均匀沉降模拟

目前，国内进行路基不均匀沉降分析时多采用余弦型不平顺[3−6]，表达式如式(2)所示：

式中：是路基不均匀沉降波长，m；为路基不均匀沉降幅值，mm。轨道高低不平顺样本与路基不均匀沉降反射至轨面的沉降叠加的垂向激励时域波形如图2所示。

1.4.3 自重荷载

路基发生不均匀沉降后，无砟轨道结构会发生跟随性沉降(如图3(b))，相当于一长波不平顺。但以往的动力学计算过程中没有考虑由于轨道自重作用产生的变形(如图3(a))。现取车速为300 km/h，路基不均匀沉降波长为20 m，沉降幅值为20 mm，分别对这2种模型进行动力学计算，计算结果对比见表3。由表3可知，考虑无砟轨道重力作用的计算结果较不考虑时偏大，分别大18%，9%和18%，可见有必要考虑轨道因自重产生的挠度，因此本文在无砟轨道承受各部件自重荷载变形完成后，再进行车辆—轨道耦合动力学计算。

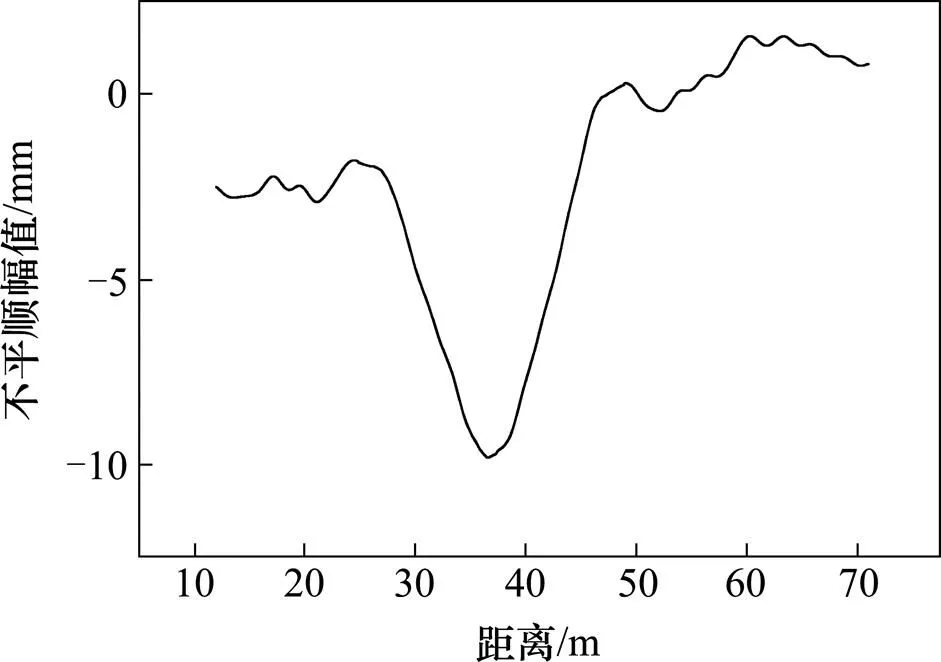
图2 叠加的垂向不平顺时域波形

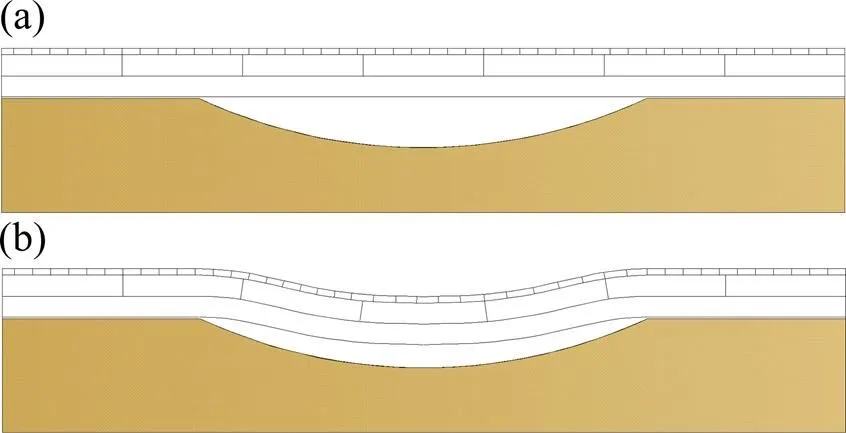
(a) 传统路基不均匀沉降下无砟轨道动力学模型；(b) 路基不均匀沉降下无砟轨道实际情况

表3 2种模型计算结果对比

2 动力响应评价标准

车体垂向振动加速度：根据文献[13]，对于高速铁路客车，车体垂向振动加速度标准为0.13 g。

轮重减载率：根据《高速试验列车客车强度及动力学规范》，轮重减载率应小于0.60。

Sperling平稳性指标：由《铁道车辆动力学性能评定和试验鉴定规范》，Sperling指标小于2.5时平稳性等级为优；在2.5~2.75之间时为良；在2.75~3.0之间时为合格。

3 模型验证

取车速为200 km/h，利用本文建立的车辆-CRTS III型板式轨道耦合动力学模型进行计算，得出钢轨、轨道板垂向位移和垂向振动加速度时程曲线如图4~7所示。与文献[14]和遂渝线上板式无砟轨道动力响应的测试结果[15]进行对比，结果见表4。

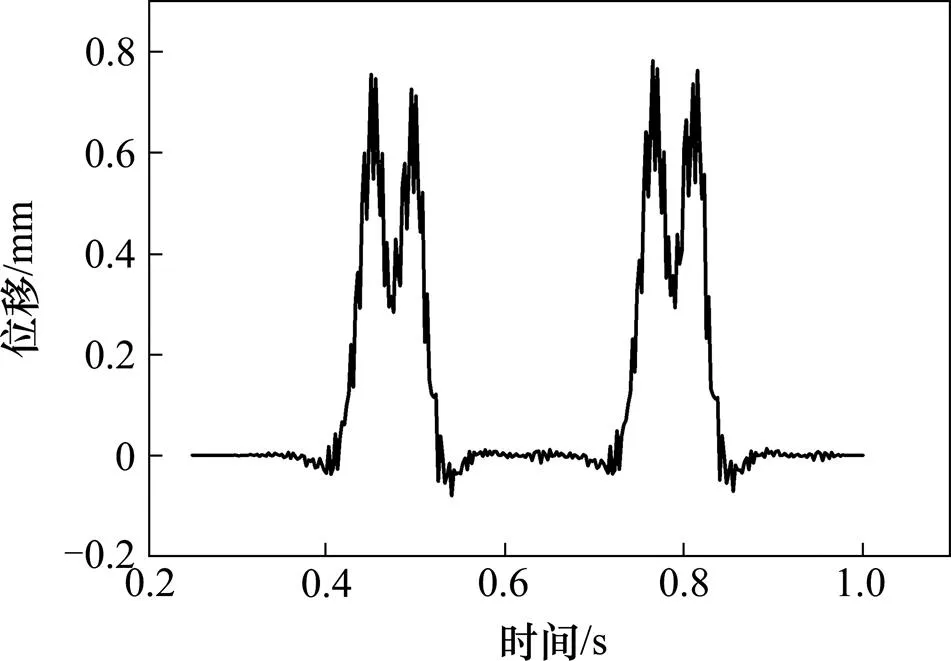
图4 最大钢轨垂向位移时程曲线

图5 最大钢轨垂向加速度时程曲线

由图4~7及表4可知，本模型得出的动力时程曲线与遂渝线动力测试结果基本相符，计算结果与遂渝线测试和参考文献计算结果比较接近。由于本文采用的轨道不平顺功率谱和文献[14]不同，且不平顺功率谱生成的样本、动力测试的结果具有随机性和偶然性，因而本文的计算结果与文献[14]和遂渝线测试结果有一定的差异是正常的。因此本文的耦合动力学模型可用于研究路基不均匀沉降对系统动力特性的影响。

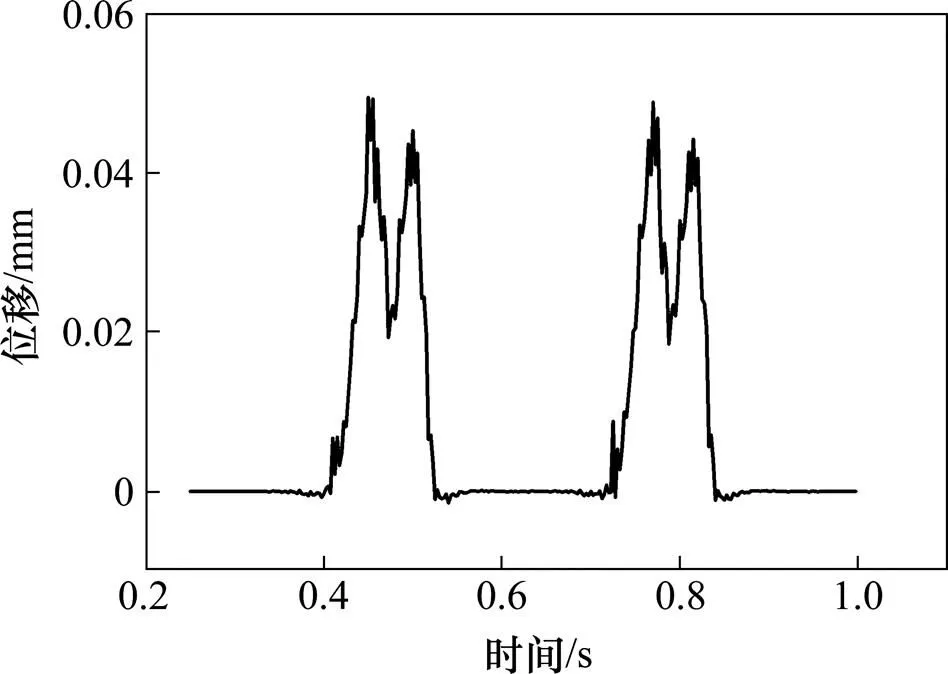
图6 最大轨道板垂向位移时程曲线

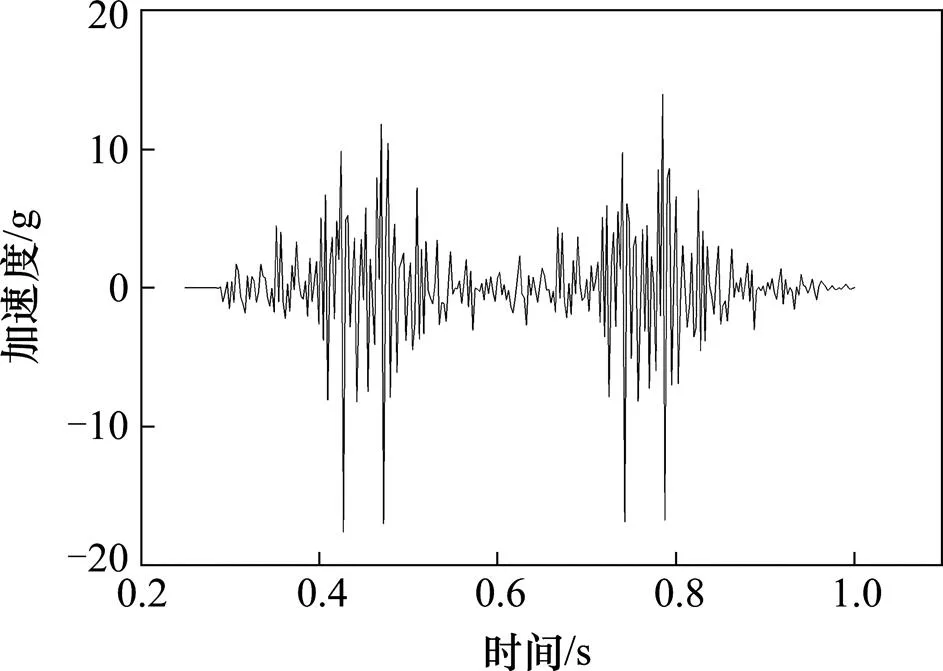
图7 最大轨道板垂向加速度时程曲线

表4 计算结果最大值比较表

4 车辆-CRTS III型轨道系统动力分析

4.1 路基不均匀沉降幅值影响分析

为研究路基不均匀沉降幅值对系统动力学指标的影响，选取代表性沉降波长为20 m，沉降幅值分别为10，20，30和40 mm4种工况，对行车速度为100，200和300 km/h时分别进行动力学计算。计算结果见图8~10。

图8 不同路基不均匀沉降幅值下车体振动加速度最大值

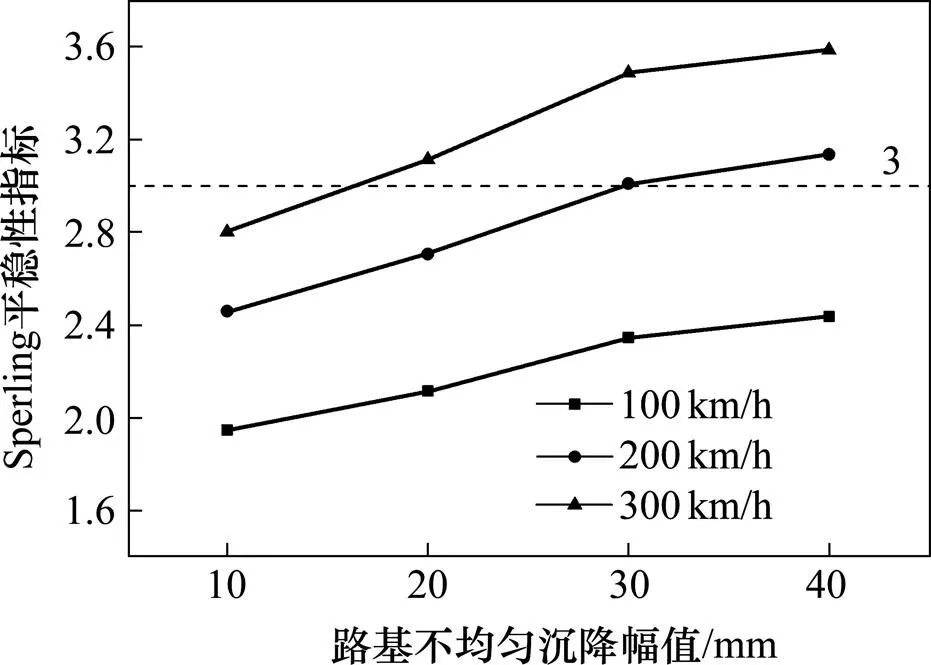
图9 不同路基不均匀沉降幅值下Sperling指标

图8为不同行车速度下，车体垂向振动加速度最大值随路基不均匀沉降幅值变化情况。由图8可知：车体垂向振动加速度随路基不均匀沉降幅值和行车速度的增加而增加，其中路基不均匀沉降幅值超过30 mm时，增加幅度有所降低，而行车速度增加时其对不均匀沉降幅值的敏感性增强。其中行车速度为100 km/h时，车体振动加速度在10~40 mm沉降幅值范围内均未超过限值0.13 g，行车速度为200 km/h时，仅在40 mm时，车体振动加速度超过限值，行车速度为300 km/h时，则在30~40 mm时超过限值。

图9为根据车体垂向振动加速度时程计算得出的Sperling平稳性指标随不均匀沉降幅值变化的情况。由图9可知：Sperling平稳性指标随路基不均匀沉降幅值和行车速度的增加而增加，沉降幅值为10~30 mm时，Sperling指标均随着沉降幅值的增加呈线性增大的趋势，大于30 mm以后，其增大的趋势变缓。其中行车速度为100 km/h时，其在10~40 mm沉降幅值范围内均未超过规范限值3，行车速度200 km/h时，仅在30 mm和40 mm时，Sperling指标超过限值，行车速度为300 km/h时，则在20~40 mm时超过限值。

图10为通过轮轨力结果计算得出的不同路基不均匀沉降幅值下轮重减载率最大值的变化情况。由图10可知：轮重减载率随路基不均匀沉降幅值和行车速度的增加相应增加，沉降幅值在10~30 mm范围内时，减载率均呈线性增大的趋势，超过30 mm以后，其对沉降幅值的敏感性增强。总体而言，轮重减载率均低于规范的要求，因而路基不均匀沉降幅值对行车的控制指标应以舒适度指标为主、安全性指标为辅。

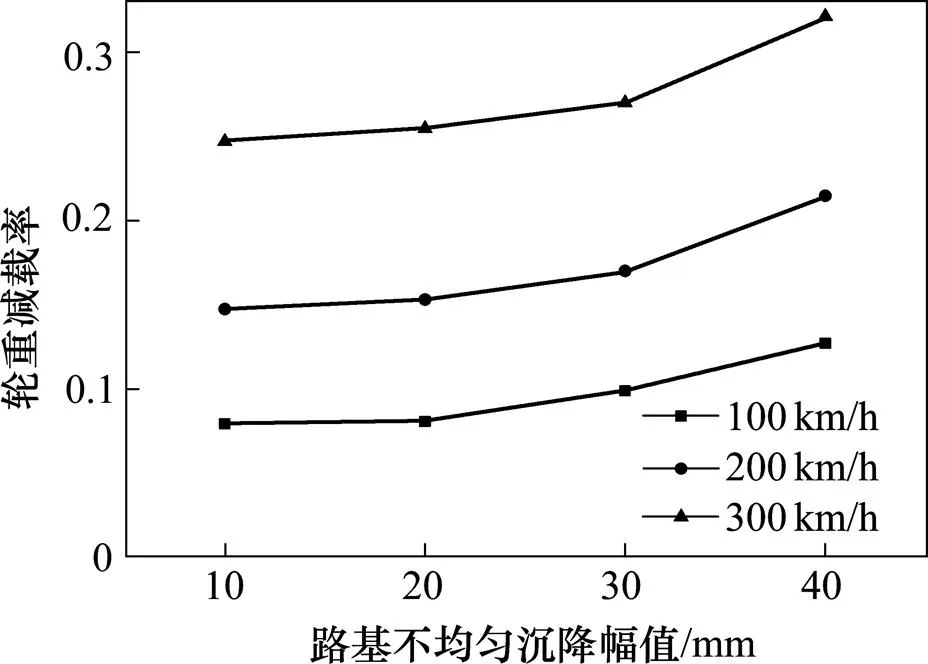
图10 不同路基不均匀沉降幅值下轮重减载率最大值

4.2 路基不均匀沉降波长影响分析

为探究CRTS Ⅲ型板式轨道路基不均匀沉降波长对系统动力响应的影响，本文考虑路基不均匀沉降波长分别为8，10，12，14，16，18，20，25，30，35和40 m共11种工况，计算在300 km/h行车速度和20 mm沉降幅值下的各项动力学指标，计算结果见图11~13。

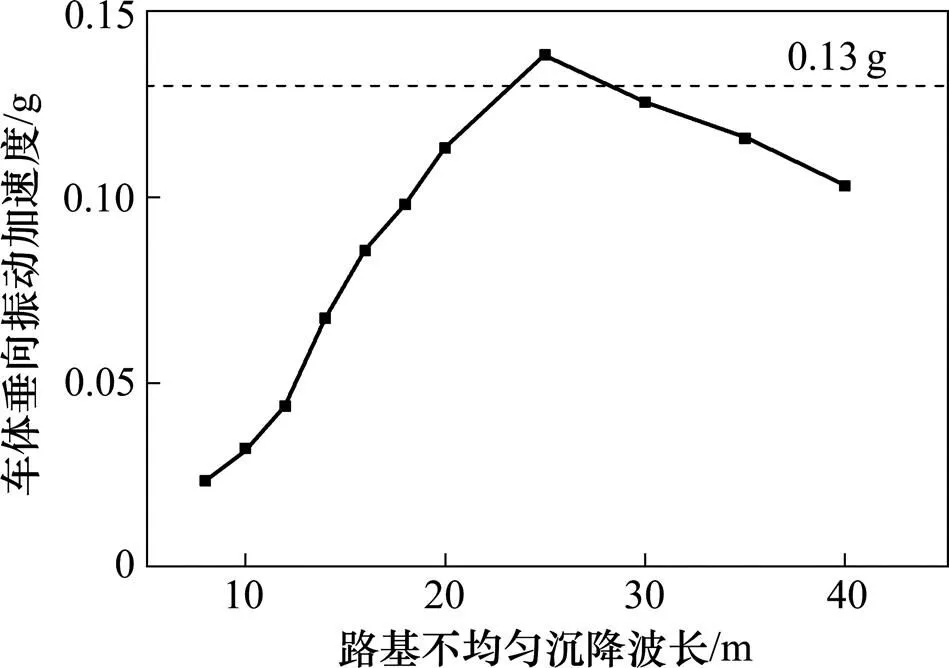
图11 不同路基不均匀沉降波长下车体振动加速度最大值

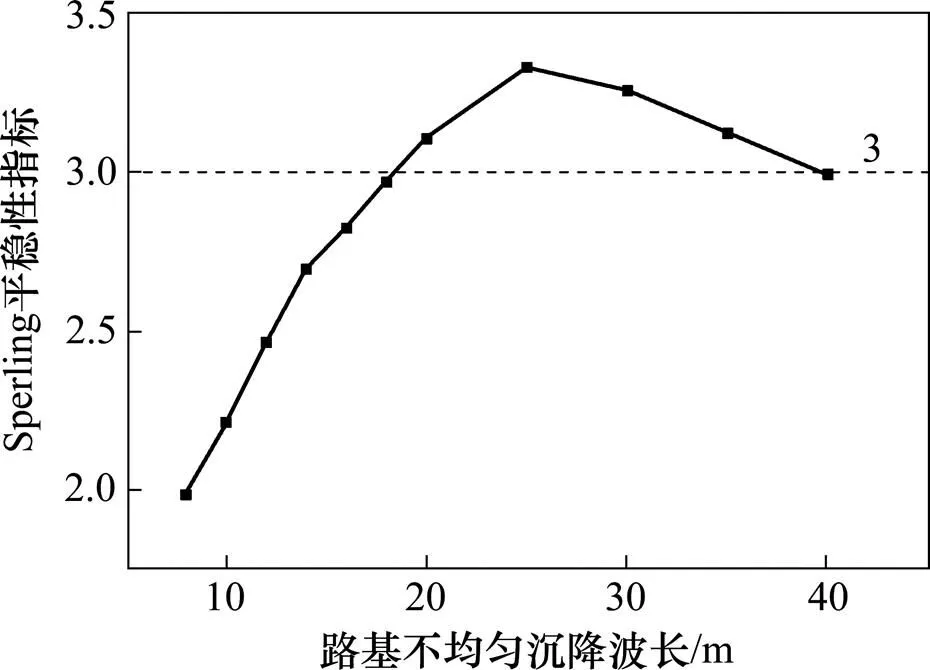
图12 不同路基不均匀沉降波长下车体Sperling指标

由图11~13可知，车体垂向振动加速度、Sperling平稳性指标和轮重减载率随波长的增加呈先增大后减小趋势，并在25 m时出现最大值。其中，车体垂向振动加速度在波长为25 m时超过规范限值；Sperling平稳性指标在波长为20~40 m时超过规范要求，在波长为20 m以下、40 m以上时合格；轮重减载率在波长超过12 m后对波长的敏感性增强，其在各种路基不均匀沉降波长下均低于规范限值的要求；所以路基不均匀沉降波长对行车的控制指标应以舒适度指标为主、安全性指标 为辅。

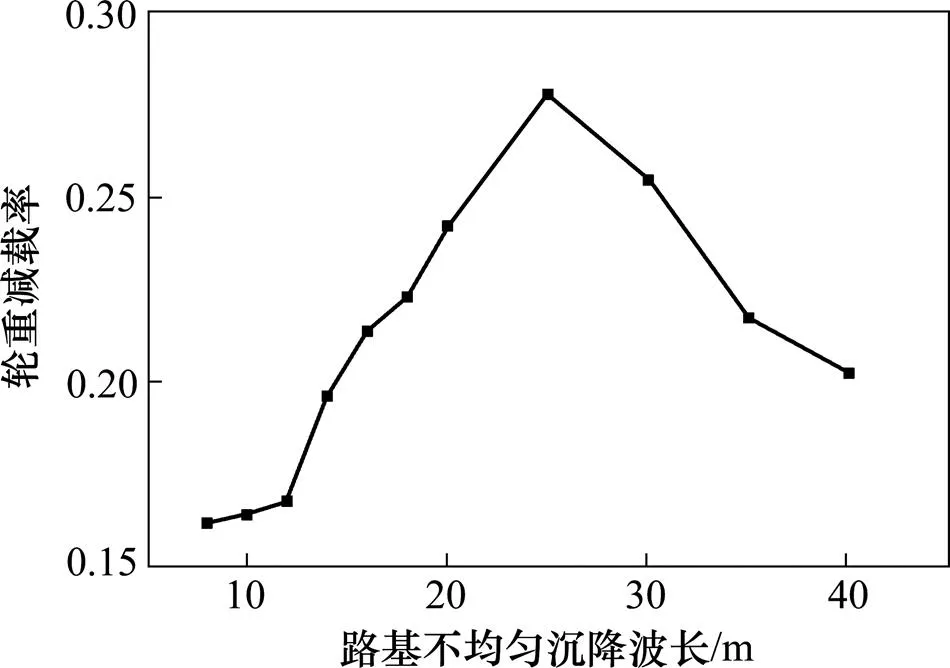
图13 不同路基不均匀沉降波长下轮重减载率最大值

总体而言，各项动力学指标均随路基不均匀沉降波长的增大呈先增大后减小的趋势。其主要原因是，波长为8~25 m时，随着波长的增大，混凝土底座板脱空范围增大，底座板抵抗变形的能力逐渐降低，轨面沉降逐渐增大并接近路基不均匀沉降幅值，表现为各项动力学指标随路基沉降波长的增加而增加；波长超过25 m后，随着波长的增加，轨面沉降不再继续增加，而轨面沉降的变坡率逐渐减小，因而表现为各项动力学指标随不均匀沉降波长的增加呈减小的趋势。

5 结论

1) 系统动力响应均随路基不均匀沉降幅值的增加而增加，行车速度增加时车体振动加速度对沉降幅值的敏感性增强，沉降幅值为20 mm，速度为300 km/h时，相关动力学指标接近或超过标准，因而不均匀沉降幅值限值应控制在20 mm/20 m以下。

2) 系统动力响应均随路基不均匀沉降波长增加呈先增大后减小的趋势，路基不均匀沉降波长对行车的控制指标应以舒适度指标为主、安全性指标为辅，在制定路基不均匀沉降限值标准时，应将波长与幅值进行综合考虑。

3) 本研究成果对CRTS Ⅲ板式轨道下路基不均匀沉降控制标准具有参考价值，采用的多体动力学和有限元联合仿真的方法实现简单，结果精确，为铁路车辆—轨道耦合振动分析提供了一种新的思路和途径。

[1] 李阳春. 武汉至咸宁城际铁路CRTSⅢ型板式无砟轨道技术[J]. 铁道工程学报, 2013, 30(4): 51−55. LI Yangchun. CRTS Ⅲ slab track technology applied in Wuhan to Xianning intercity railway[J]. Journal of Railway Engineering Society, 2013, 30(4): 51−55.

[2] 李中华. CRTSⅠ型与CRTSⅡ型板式无砟轨道结构特点分析[J]. 华东交通大学学报, 2010, 27(1): 22−28. LI Zhonghua. An analysis on structural characteristics of CRTSⅠand CRTSⅡslab ballastless track[J]. Journal of East China Jiaotong University, 2010, 27(1): 22−28.

[3] 徐庆元, 范浩, 李斌, 等. CRTS-II型板式无砟轨道线路路基不均匀沉降限值研究[J]. 中南大学学报(自然科学版), 2013, 44(12): 5038−5044. XU Qingyuan, FAN Hao, LI Bin, et al. Limited value for uneven settlement of subgrade under CRTS-II type slab track[J]. Journal of Central South University (Science and Technology), 2013, 44(12): 5038−5044.

[4] 张小会, 周顺华, 宫全美, 等. 路基不均匀沉降对车辆和轨道动力响应的影响[J]. 同济大学学报(自然科学版), 2015, 43(8): 1187−1193. ZHANG Xiaohui, ZHOU Shunhua, GONG Quanmei, et al. Effect of subgrade differential settlement on dy­namic response of vehicle and slab track vertical coupled system[J]. Journal of Tongji University (Natural Science), 2015, 43(8): 1187−1193.

[5] 肖威. 路基不均匀沉降对CRTS Ⅲ型板式无砟轨道力学特性的影响[D]. 成都: 西南交通大学, 2015. XIAO Wei. Effect of uneven subgrade settlement on mechanic characteristics of CRTS Ⅲ slab track in high-speed railway[D]. Chengdu: Southwest Jiaotong University, 2015.

[6] 韩义涛, 姚力. 基础沉降对土路基上板式轨道动力性能影响分析[J]. 铁道工程学报, 2007, 24(10): 28−31. HAN Yitao, YAO Li. Analysis of the dynamic performance for slab track settlement on embankment[J]. Journal of Railway Engineering Society, 2006, 24(10): 28−31.

[7] Gong C, Iwnicki S, Bezin Y. The effect of railway vehicle dynamics on the lateral alignment of track[J]. Journal of Rail & Rapid Transit, 2016, 230(1): 258−270.

[8] Steenbergen M J M M, Metrikine A V, Esveld C. Assessment of design parameters of a slab track railway system from a dynamic viewpoint[J]. Journal of Sound & Vibration, 2007, 306(1): 361−371.

[9] 缪炳荣, 罗仁, 王哲, 等. SIMPACK动力学分析高级教程[M]. 成都: 西南交通大学出版社, 2008. MIAO Bingrong, LUO Ren, WANG Zhe, et al. Advanced tutorial of dynamic analysis[M]. Chengdu: Journal of Southwest Jiaotong University, 2008.

[10] Rathod C, Shabana A A. Modeling structural flexibility in railroad vehicle systems[C]// Joint Rail Conference, Urbana, Illinois, USA, April 27−29, 2010: 179−189.

[11] 殷学纲, 陈淮, 赛开林. 结构振动分析的子结构方法[M]. 北京: 中国铁道出版社, 1991. YIN Xuegang, CHEN Huai, SAI Kailin. Substructure method of structural vibration analysis[M]. Beijing: China Railway Press, 1991.

[12] 高建敏. 高速铁路无砟轨道不平顺谱的比较分析[J]. 铁道科学与工程学报, 2015(4): 715−723. GAO Jianmin. Comparative analysis of power spectrum density of ballastless track irregularities of Chinese high-speed railway[J]. Journal of Railway Science and Engineering, 2015(4): 715−723.

[13] 翟婉明. 车辆—轨道耦合动力学[M]. 3版. 北京: 科学出版社, 2007. ZHAI Wanming. Vehicle-track coupling dynamics[M]. 3rd ed. Beijing: Science Press, 2007.

[14] 罗震. 高速铁路无砟轨道结构受力及轮轨动力作用分析[D]. 成都: 西南交通大学列车与线路研究所, 2008: 68−79. LUO Zhen. Analysis of structure mechanics and wheel/rail dynamic interaction of ballastless track in high-speed railway[D]. Chengdu: Train & Track Research Institute, Southwest Jiaotong University, 2008: 68−79.

[15] 西南交通大学列车与线路研究所. 遂渝线路基地段无砟轨道动力性能测试研究报告[R]. 成都: 西南交通大学, 2007: 11−18. Train & Track Research Institute of Southwest Jiaotong University. Experiment report of dynamic characteristic of ballastless on subgrade of Sui-Yu test section[R]. Chengdu: Southwest Jiaotong University, 2007: 11−18.

(编辑 阳丽霞)

Influence of subgrade uneven settlement on dynamic characteristic of vehicle-CRTSⅢ slab track system

TANG Jinfeng, LIU Wenfeng, WANG Hao, QIN Zhi

(School of Civil Engineering, Central South University, Changsha 410075, China)

In order to study the dynamic influence of subgrade uneven settlement on vehicle-CRTS Ⅲ slab track system, the response of vehicle and slab track system is calculated with multi-body dynamics and FEM respectively, and the two subsystems are coupled with wheel-rail relationship. A vehicle-CRTS Ⅲ slab track 3-D coupled dynamic model that the gravity is considered was established later. Then, the factors that affect the dynamic respond including speed, magnitude and wavelength of the settlement were researched. Results indicate that the response increases with the increasing of speed and the magnitude of subgrade uneven settlement, the limit value of the uneven settlement magnitude affecting driving is controlled by the comfort index, and it should be controlled less than 20 mm/20 m. The dynamic response increases first and then decreases with the increasing of the uneven settlement wavelength. The magnitude and wavelength of the uneven settlement should be considered together when setting the standard for the subgrade uneven settlement.

CRTS III slab track; subgrade uneven settlement; co-simulation; dynamic response

10.19713/j.cnki.43−1423/u.2018.10.001

U211.5；U213

A

1672 − 7029(2018)10 − 2455 − 08

2017−09−08

国家自然科学基金资助项目(51578552)

唐进锋(1965−)，男，湖南常德人，副教授，从事列车—轨道耦合动力学研究；E−mail：csutjf@csu.edu.cn