基于TMD的自锚式人行悬索桥人致振动控制研究

邹卓，宋旭明，李璋, 2，唐冕，贺锃



基于TMD的自锚式人行悬索桥人致振动控制研究

邹卓1，宋旭明1，李璋1, 2，唐冕1，贺锃1

(1. 中南大学 土木工程学院，湖南 长沙 410075； 2. 天津市市政工程设计研究院，天津 300051)

现代大跨轻型人行桥很难满足我国现行《城市人行天桥与人行地道技术规范》(CIJ69-95)对人行桥基频不小于3 Hz的要求。对比分析其他国家人行桥舒适度评价标准和规范发现，限制动力响应值法相比频率调整法更适合现代大跨轻型人行桥设计。为了给我国制定人行桥振动舒适度评价标准提供依据，以一座双塔三跨自锚式钢箱梁人行悬索桥为工程背景，建立有限元模型，计算结构动力特性，依据EN03-2007和ISO10137规范确定人行荷载模式，并进行加速度响应分析和舒适度评价。以无阻尼结构调谐质量阻尼器(TMD)最优参数为初始值，优化TMD与主体结构的质量比和频率比，确定合理的减振控制方案。计算结果表明，自锚式人行悬索桥在附加与主梁质量比为1.5%的TMD后人致振动减振率为70.9%~81.7%，可达到相关规范最好舒适度要求。

自锚式人行悬索桥；步行荷载；人致振动；舒适度评价；减振设计

自锚式悬索桥造型优美，适应性强，在城市桥梁尤其是人行桥中应用日益广泛。自锚式人行悬索桥具有自振周期长、振型密集的特点，自振频率容易与行人的步频相接近，引起共振现象，给桥上行人带来不适，甚至危及桥梁的安全。目前，国内外均有相应的标准和规范来评价人行桥舒适度。英国BS5400规范、瑞典Bro2004规范、德国人行桥设计指南(EN03-2007)及国际标准化组织ISO10137规范均采用加速度峰值或者均方值作为舒适度评价的指标，但是各国规范规定的荷载模式和加速度限值都有所差异。我国《城市人行天桥与人行地道技术规范》(CIJ69-95)要求人行桥基频不小于3 Hz，这对于现代大跨轻型的人行桥很难实现。依据动力学基本原理，人行桥在步行荷载下的反应受激励条件、结构的刚度、质量和阻尼等多种因素控制[1]。规范仅从自振频率对结构提出了要求，无法保证设计的合理性与有效性[2]。一些学者对人行桥的人致振动及其减振方法进行了大量的研究。1956年，Den Hartog最早研究了无阻尼和有阻尼的减震器理论，并提出了减震器的基本原理和最优参数的确定方法。Brownjohn等[4]对新加坡某座人行桥进行实测，研究桥上的静止(或行走)人群对结构频率和阻尼的影响。法永生等[5]建立适合于评估人行桥振动烦恼率的舒适度量化指标，提出考虑人行桥竖向与侧向耦合振动时的综合评价方法。陈政清等[6]研究人行桥的人致振动理论及动力设计方法，阐述了人行桥横向振动分析的主要理论。Pedersen等[7]研究人行桥对随机荷载模型参数的振动敏感性，并提出单人竖向步行力动载系数。钱骥等[8]提出大跨径人行桥人致振动舒适性评估指标，并对某人行桥进行基于调频质量阻尼器的减振措施预案设计。李红利等[9]基于响应谱方法对人行桥的人致振动响应进行了较系统的研究。朱俊朋等[10]采用调谐质量阻尼器(MTMD)对人行悬索桥进行振动控制。目前的文献资料显示，虽然国内外研究人员对人致振动进行了大量研究，但针对自锚式人行悬索桥的人致振动及其振动控制的研究很少。本文计算一座双塔三跨自锚式钢箱梁人行悬索桥的结构动力特性，根据不同规范进行加速度响应分析和舒适度评价，并优化TMD参数，确定合理的减振控制方案。研究结果可为我国制定人行桥振动舒适度评价标准提供依据，也对类似桥梁的减振控制分析具有重要参考价值。

1 人致振动及振动控制理论

人行桥的人致振动计算即应用动力学方法计算人行桥在行人荷载激励下的动力响应，以此评价行人的舒适度。因此，首先需确定人行荷载模式及舒适度评价标准。

1.1 人行荷载模式及舒适度评价标准

一些学者提出了不同的人行荷载模型，主要有周期荷载模型、Dallard荷载模型[11]、Nakamura荷载模型[12]和孙利民—袁旭斌模型[13]等。其中，周期荷载模型为最简单的荷载模式，被诸多国家广泛运用于人行桥的设计中。有别于我国规范对人行桥振动控制采用的频率调整法，国外规范大多采用限值动力响应值法来控制结构的振动响应。

英国BS5400规范只考虑单人荷载模式下行人匀速通过桥梁时的人行桥振动响应，采用Blanchard提出的人行桥竖向振动舒适度限值函数，将峰值加速度作为舒适度评价指标。瑞典Bro2004规范用一个幅值和频率不变的正弦荷载来表示人群对桥梁的荷载激励作用，再将荷载模式计算的等效人群荷载施加于结构最大加速度响应位置处，分析所选控制截面在各荷载工况下的动力响应，用均方根加速度作为人行桥振动舒适度评价指标。在德国人行桥设计指南(EN03-2007)中，每个横向或竖向振型逐个计算，得到在规定行人密度或者行人数下的加速度最大响应。该规范的行人舒适度评价指标是由人行桥的加速度来表示，根据人体对加速度的感觉强度，将舒适度分为4个舒适级别。国际化标准组织ISO10137规范分单个行人的荷载标准与人群荷载标准2个类别，基于振动舒适度基准曲线，给出了行人以不同步频行走时人行桥振动舒适度的临界曲线，考虑的因素有振动方向、有效加速度、振动持续时间和振动频率等，对舒适度的评价比较 全面。

对比以上规范可以发现，各规范对人行荷载标准及舒适度指标的规定均存在差异。BS5400规范仅考虑了单个行人在桥上行走时的竖向荷载；Bro2004仅考虑人群非一致步伐行走下的竖向荷载模式；德国EN03(2007)不仅考虑了竖向荷载和侧向荷载，而且根据不同人群密度选取了不同的荷载模式；ISO10137标准既考虑单人作用和人群作用，也考虑了行人竖向荷载和侧向荷载。由于人体对横向加速度的感知比对竖向加速度的感知敏感得多，故BS5400规范和Bro2004规范考虑得还不够全面，而EN03和ISO10137对竖向及横向上都有具体的荷载模式和舒适度指标，本文选用这2种规范进行舒适度评价。

1.2 人致振动控制

改善桥梁动力特性有2种方法：第1种方法是增大桥梁的刚度，使固有频率偏离行人步行力的基频范围。增加刚度往往伴随着质量的增大，自振频率的提高有限。第2种方法是提高桥梁的阻尼以减少共振效应，主要措施有调谐质量阻尼器(TMD)、调谐液体阻尼器(TLD)和黏滞阻尼器等。

TMD为附加在主结构上的阻尼装置，由固体质量块、弹簧和阻尼组成。单自由度结构附加TMD的减振控制模型如图1所示。

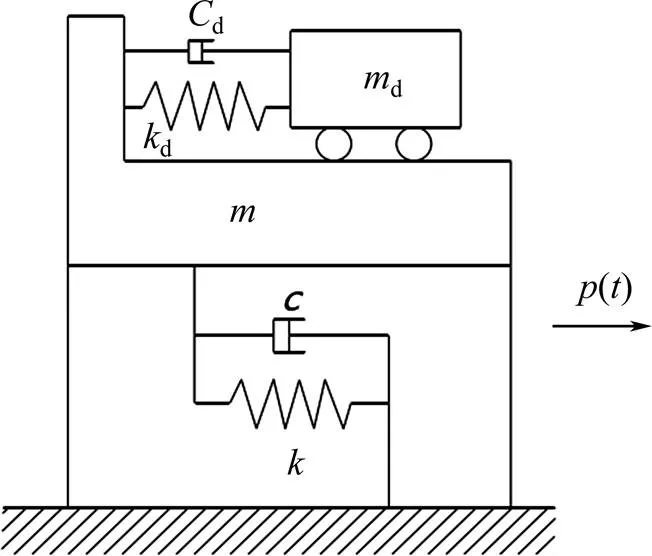
图1 主结构-TMD计算模型

图1所示附加TMD的结构的运动方程为：

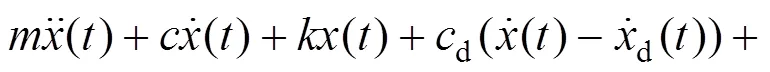
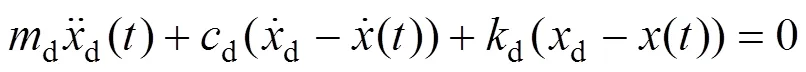
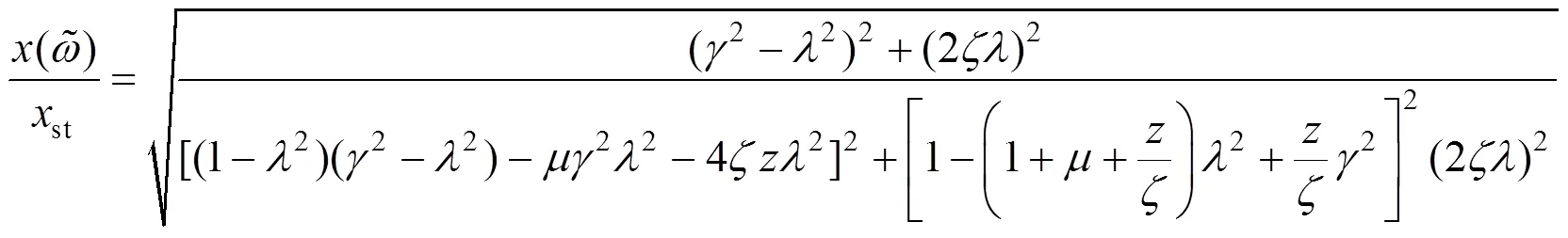
由式(2)可知，将阻尼器系统的自振频率调至与主结构的振动的频率相近时，在外荷载激励作用下，TMD系统将随着主结构的振动而振动，同时作用一个反向力于主结构上，实现能量从主结构向调谐质量阻尼器系统的转移，达到减少主结构振动响应的目的。

选取合适TMD参数对TMD的减振效果起着决定性的作用，TMD参数包括与广义质量的质量比、频率比和阻尼比。Den Hartog在1956年首次提出无阻尼结构的TMD参数优化方法[1]，该方法以主结构受到简谐荷载激励时的稳定状态为目标来确定TMD的最优参数：

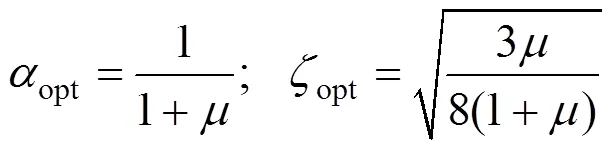
引入阻尼后，一般通过数值方法确定TMD的最优频率比和阻尼比。对于小阻尼结构，可将无阻尼结构最优参数为初始值，通过优化计算得到该结构的TMD合理参数。

2 自锚式人行悬索桥动力特性及人致振动分析

2.1 工程概况及计算模型

本文工程背景为一座双塔三跨自锚式钢箱梁人行悬索桥，全长220 m，加劲梁跨径组合为(50+120+50) m。钢箱梁宽4 m，两侧设置0.5 m宽的风嘴，梁高1.3 m，为单箱单室闭合截面，主缆及吊索中心距为3.4 m，主缆计算矢跨比为1/5。

主梁采用Q345钢；主缆采用塑料护套平行钢丝索PES7-139，标准强度1 670 MPa，LM7型冷铸墩头锚；吊杆采用PES5-13，标准强度1 670 MPa，聚乙烯护套，热铸Ⅰ型锚具。主塔为C35混凝土。各构件材料及截面特性如表1所示。

采用midas civil建立自锚式钢箱梁人行悬索桥有限元模型，全桥共353个节点，216个梁单元，138个索单元。桥塔基础为固结，约束主梁梁端竖向自由度，主梁与主塔间为竖向弹性支撑。全桥有限元模型如图2所示。

2.2 结构动力特性

结构的自振频率及各阶振型可通过模态分析获得，该桥前58阶振动频率均在5 Hz以内，振动模态有纵向、竖向、横向、扭转和缆索振动。由于各国规范所规定的行人荷载模式为横向和竖向，故选取第2，3，17，20和31阶模态计算主梁的竖向和横向加速度响应，并进行舒适度评价。结构的主要振型如表2所示，部分振动模态如图3所示。

表1 材料及截面特性

图2 自锚式人行悬索桥有限元模型

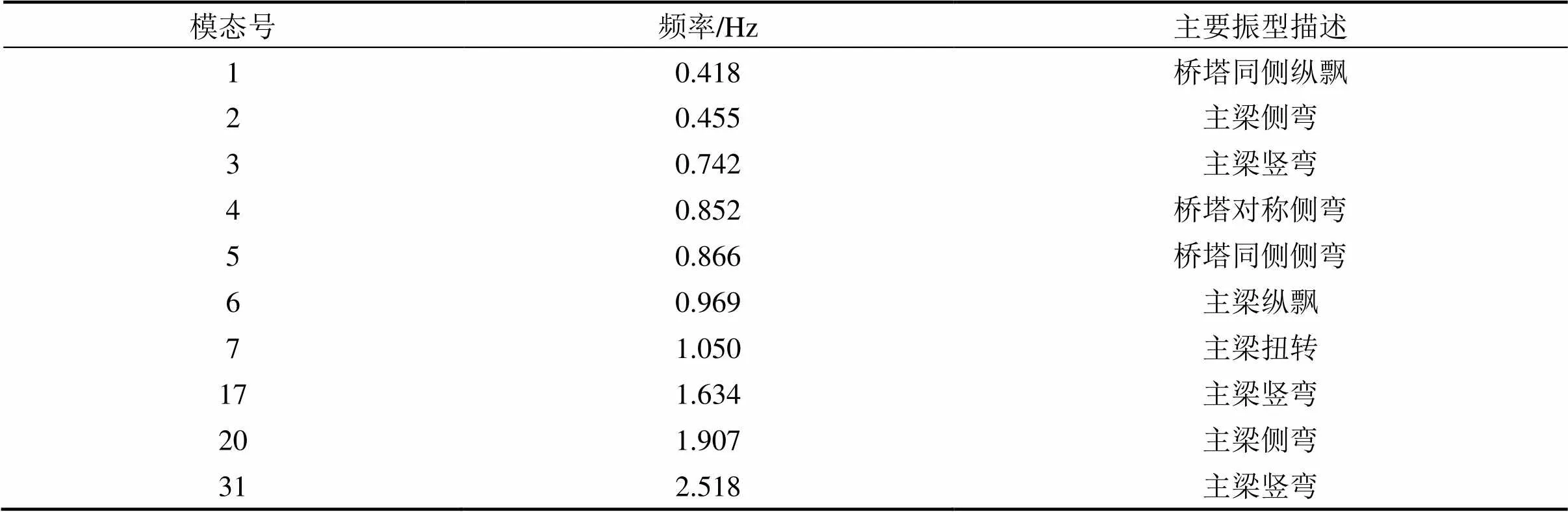
表2 主要振型描述

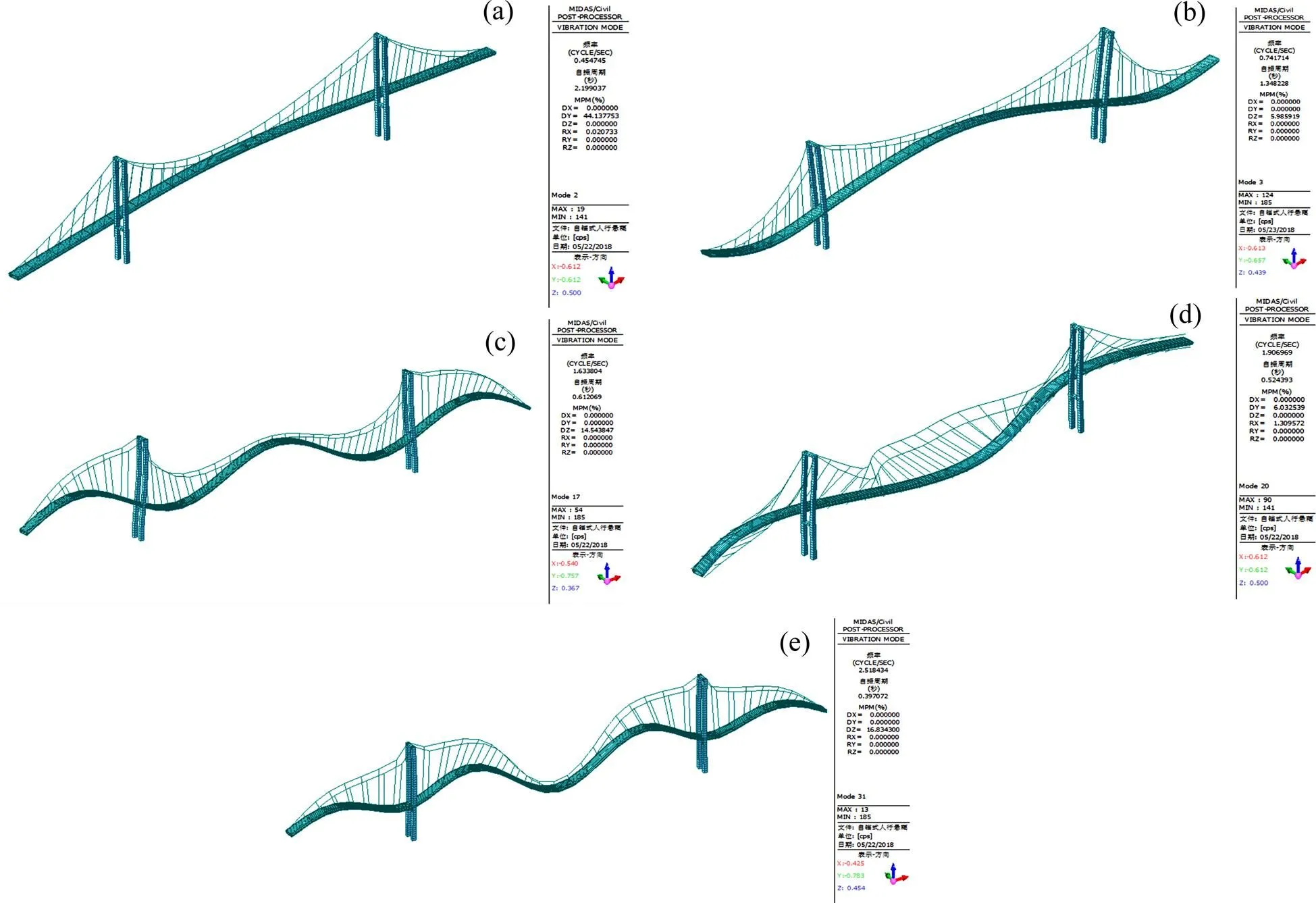
(a) 第2阶模态振型；(b) 第3阶模态振型；(c) 第17阶模态振型；(d) 第20阶模态振型；(e) 第31阶模态振型

2.3 舒适度评价

从表2可以看出，第17和31阶模态的频率分别为1.634 Hz和2.518 Hz。依据EN03-2007，在人行步频范围内共振可能性非常大，故取第17和31阶模态计算竖向共振下的最大加速度响应。第2和20阶模态的频率分别为0.455 Hz和1.907 Hz，离横向敏感频率很近，取这2阶模态计算横向共振下的最大加速度响应。

EN03-2007规定在一定人行密度下，产生最大加速度的等效均布荷载为：

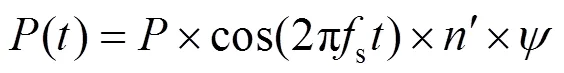
式中：s为步频，等于所考虑的人行桥的自振频率；是步频为s时，单人行人产生的荷载幅值；′为等效行人密度；为考虑到步频接近基频变化范围临界值的概率而引入的折减系数。

将依据式(4)求得的各模态下的等效均布荷载施加在该人行桥上，再选取主跨有代表性的1/8截面、1/4截面、3/8截面以及跨中截面作为控制截面，计算振动加速度响应，并进行舒适度评价，结果如表3所示。

由表3可知，第20阶模态下各截面位置舒适度指标较好，只需针对第17阶模态、第31阶模态和第2阶模态采取减振措施。

根据ISO10137规范，人群荷载等效为周期性运动的均布荷载，一致步伐行走时采用的荷载模式为：

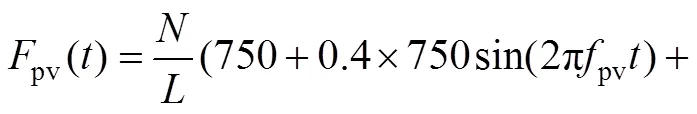
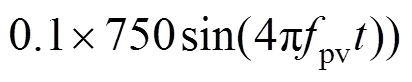
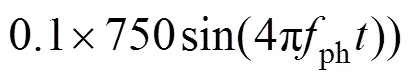
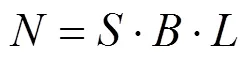
利用上述荷载模式得到的部分模态加速度响应如图4所示。

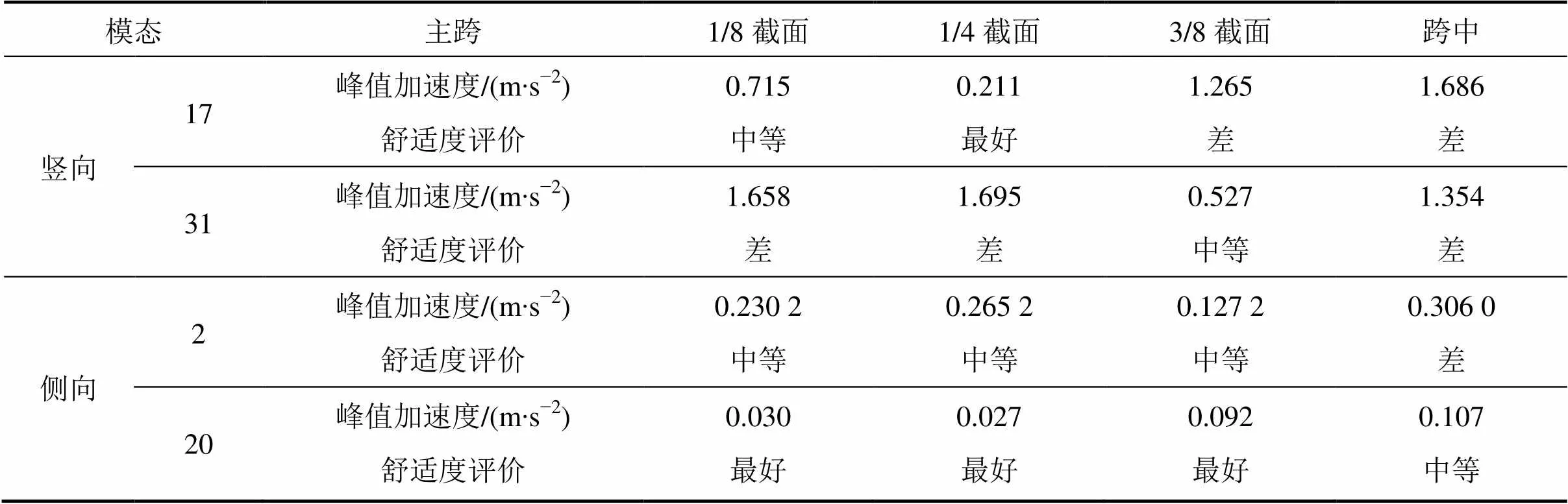
表3 基于EN03-2007的加速度分析结果及舒适度评价

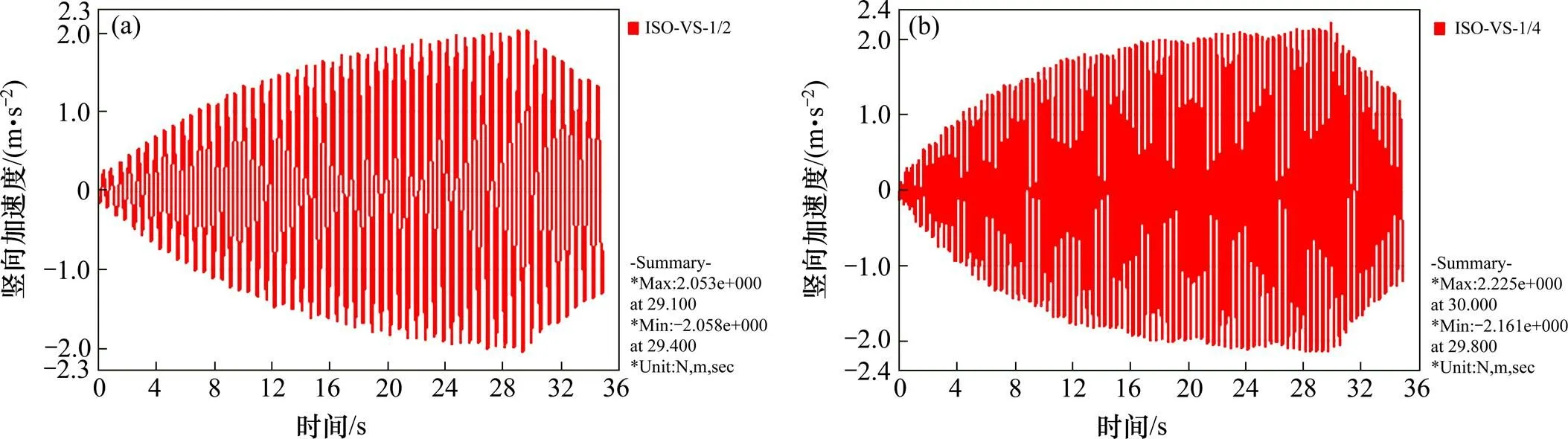
(a) 模态17跨中截面的竖向加速度；(b) 模态31下1/4截面的竖向加速度

依据ISO10137计算人群荷载下该桥舒适度，可知第17阶模态的均方加速度为0.120~2.503 m⁄s2，第31阶模态下的均方加速度为0.258~2.225 m⁄s2，均不能满足舒适度要求，需采取相应的减振措施。

3 基于TMD的自锚式人行悬索桥振动控制及参数分析

3.1 TMD参数分析

以无阻尼结构TMD最优参数为初始值，针对不同模态下TMD参数进行敏感性分析并确定有阻尼结构TMD最优参数。由于第2阶、第17阶和第31阶模态在跨中部位均有较大的模态位移，为简化起见，在进行参数分析时，将TMD设置在中跨跨中部位，待确定TMD最优参数之后再进行TMD数量及位置的设计。

3.1.1 质量比

第2阶模态振型为侧弯曲，模态质量为522.45 t，依据Den Hartog提出的最优参数的计算方法，计算得各最优参数见表4。

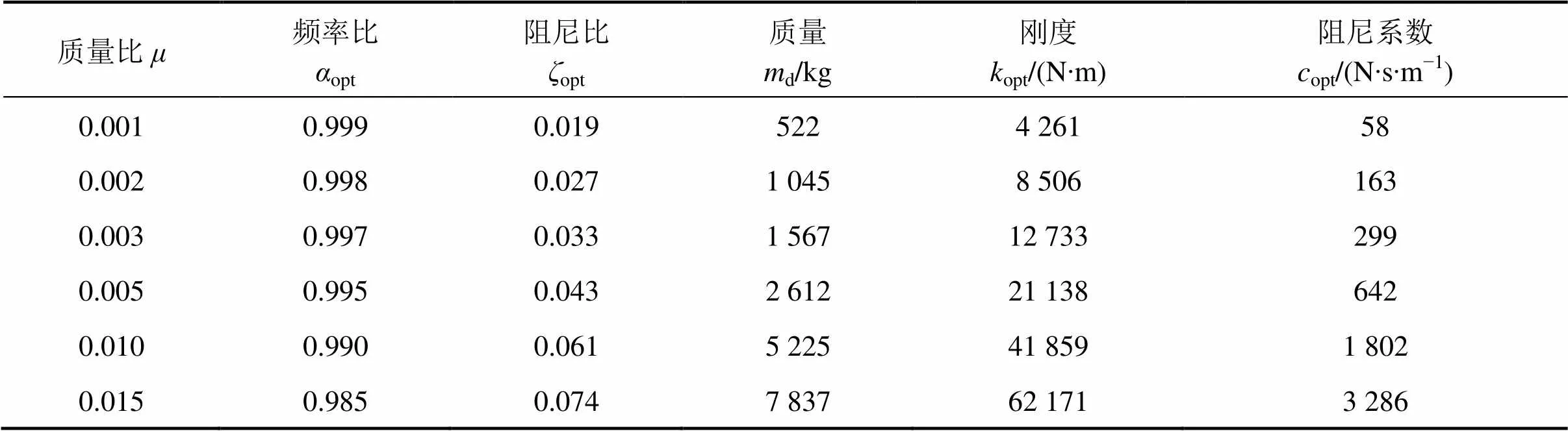
表4 结构无阻尼时第2阶模态TMD最优参数

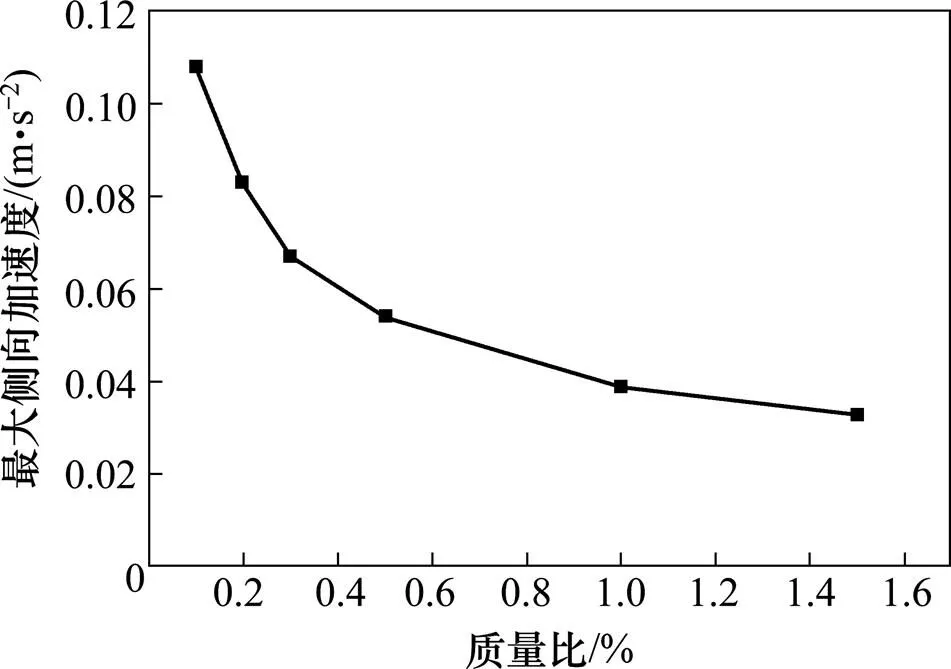
图5 不同质量比下最大加速度

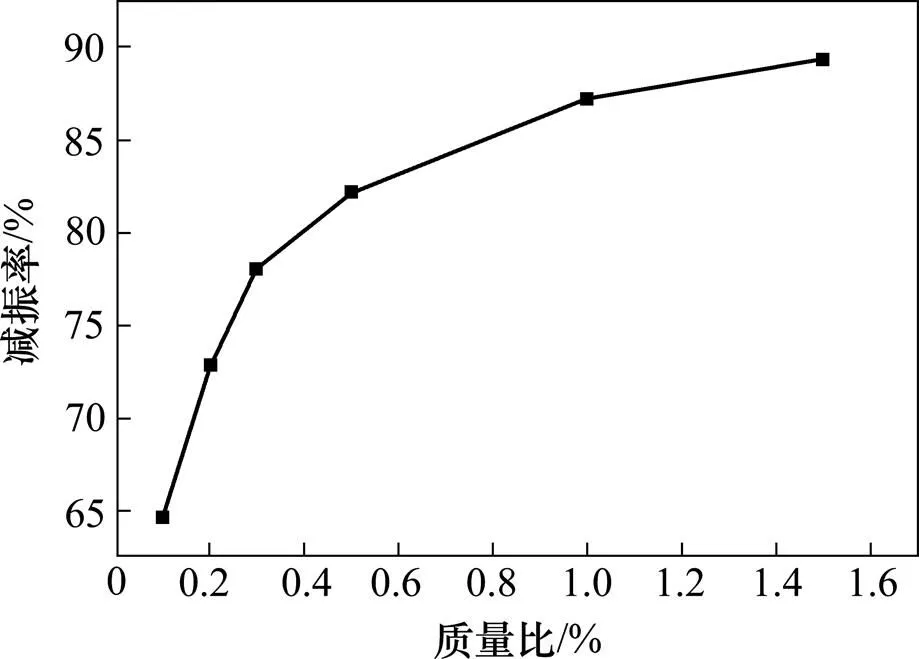
图6 不同质量比下TMD减振率

不同TMD质量比下的最大加速度及减振率见图5和图6。

从图6可知，质量比越大减振效果越好，但随着质量比的增大减振率并非线性增加，而是随着质量比的增大趋于平缓，过大的质量比将增加TMD的安装难度、对结构的承载力不利而且也不经济。从图5可知，当TMD质量比为0.2%时，结构最大侧向加速度为0.081 m/s2，已经到达规范舒适度最好的级别，故选取第2阶模态TMD质量为1 045 kg(0.2%质量比)。同理，可选取第17和31阶模态TMD质量为1 721 kg(1%质量比)和1 992 kg(1%质量比)。

3.1.2 频率比

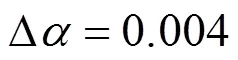
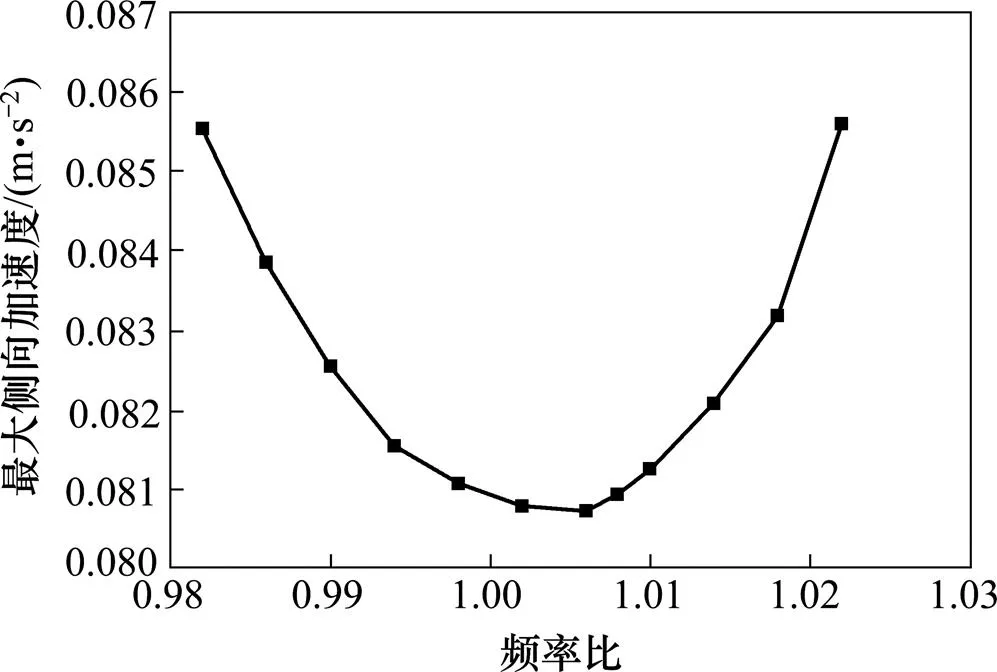
图7 频率比与最大侧向加速度关系图

由图7可知，在频率比变化时，侧向加速度变化幅度相对较小，在TMD频率比为1.006时，最大侧向加速度达到最小值，因此，选取第2阶模态TMD频率比为1.006。计算表明，在频率比变化时，竖向加速度变化幅度也相对较小，在第17和第31阶竖弯模态下TMD的最优频率比分别为1.005和0.980。

3.2 TMD设置方案

TMD一般都安装在各模态振型位移最大处，以获得最佳的减振效果。第2阶模态为侧弯，该模态位移只有主跨跨中处1个极值点，故将TMD置于中跨跨中位置。第17阶模态为竖弯，振型位移有5个极值点，分别位于两边跨跨中、主跨两1/8跨和主跨跨中处。根据各极值点的分布，在TMD总质量(1 721 kg)，总刚度(183 222 N/m)和总阻尼(2 120 N∙s/m)不变的情况下，设计如表5所示4种方案，并计算各工况下最大竖向加速度响应及减震率。

由表5可知，虽然方案2，3和4的TMD质量在桥上分布更为均匀，但是减振效果比方案一稍差。采用相同的计算方法，可确定第31阶模态下TMD的合理设置方案为2个阻尼器(总质量为1 992 kg，总刚度为478 865 N/m，总阻尼为3 782 N∙s/m)分别置于中跨1/4跨。

安装TMD前后基于EN03和ISO10137的人行荷载作用下桥梁不同位置加速度响应如图8~9 所示。

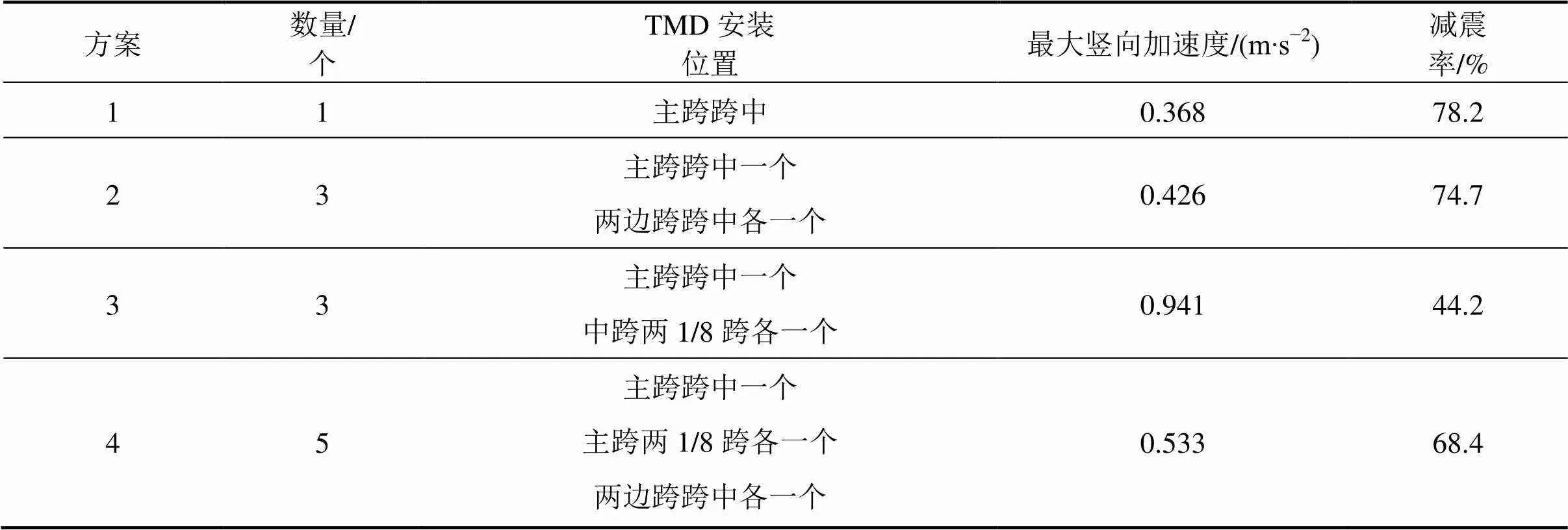
表5 第17阶模态TMD安装方案

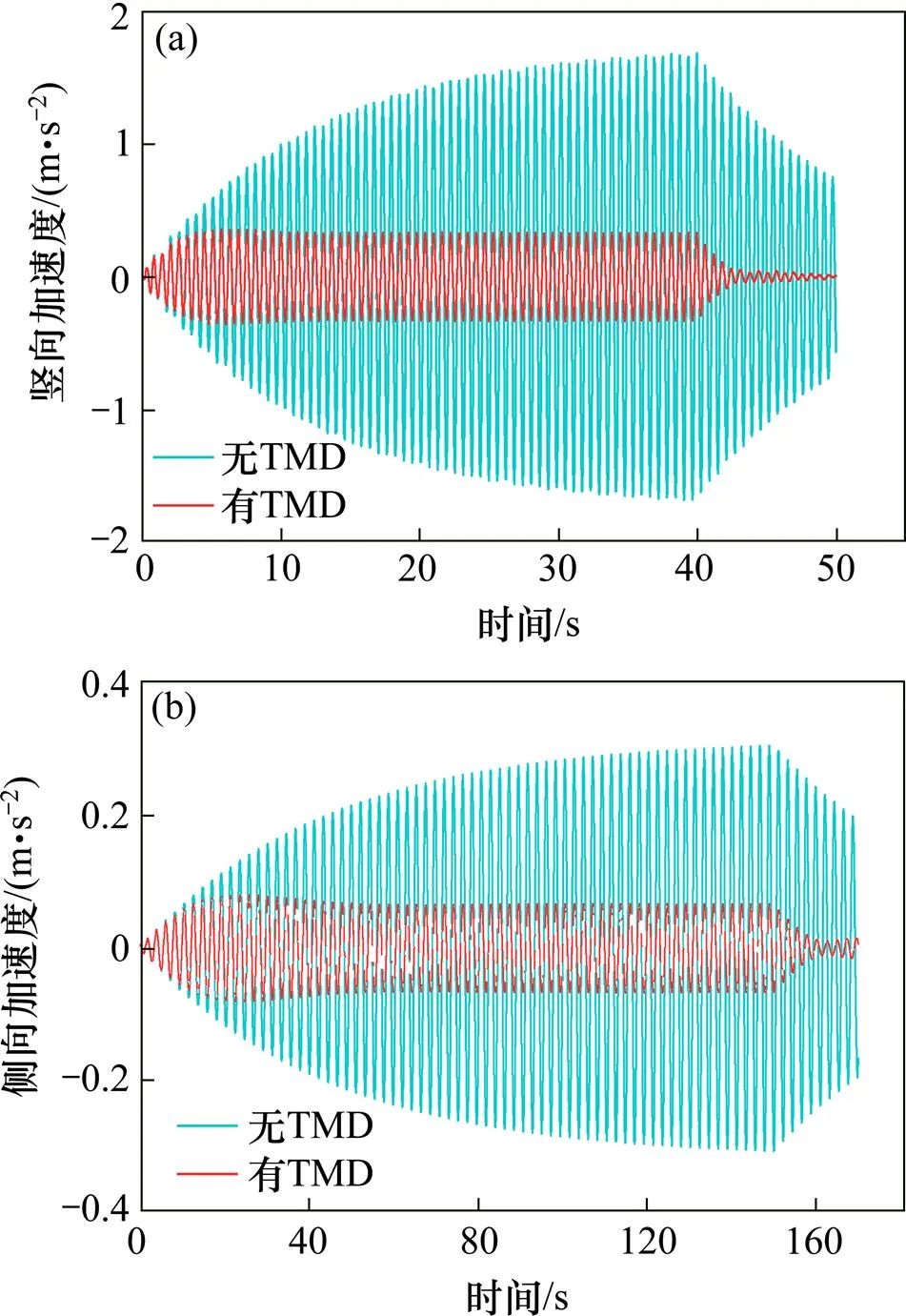
(a) 模态17跨中截面的竖向加速度； (b) 模态2跨中截面的侧向加速度

由图8~9可知，安装TMD后各工况加速度均大幅度降低，减振率达70.9%~81.7%，各工况均能满足舒适度要求。在人行荷载激励时间段，各工况加速度由原来趋于发散状态很快就进入稳定状态；取消激励荷载后，结构加速度也能更快衰减，可见调谐质量阻尼器对控制振动有很好的效果。总TMD质量仅为主梁质量(307.2 t)的1.5%，可置于箱梁内部，不影响桥梁的美观及承载力。

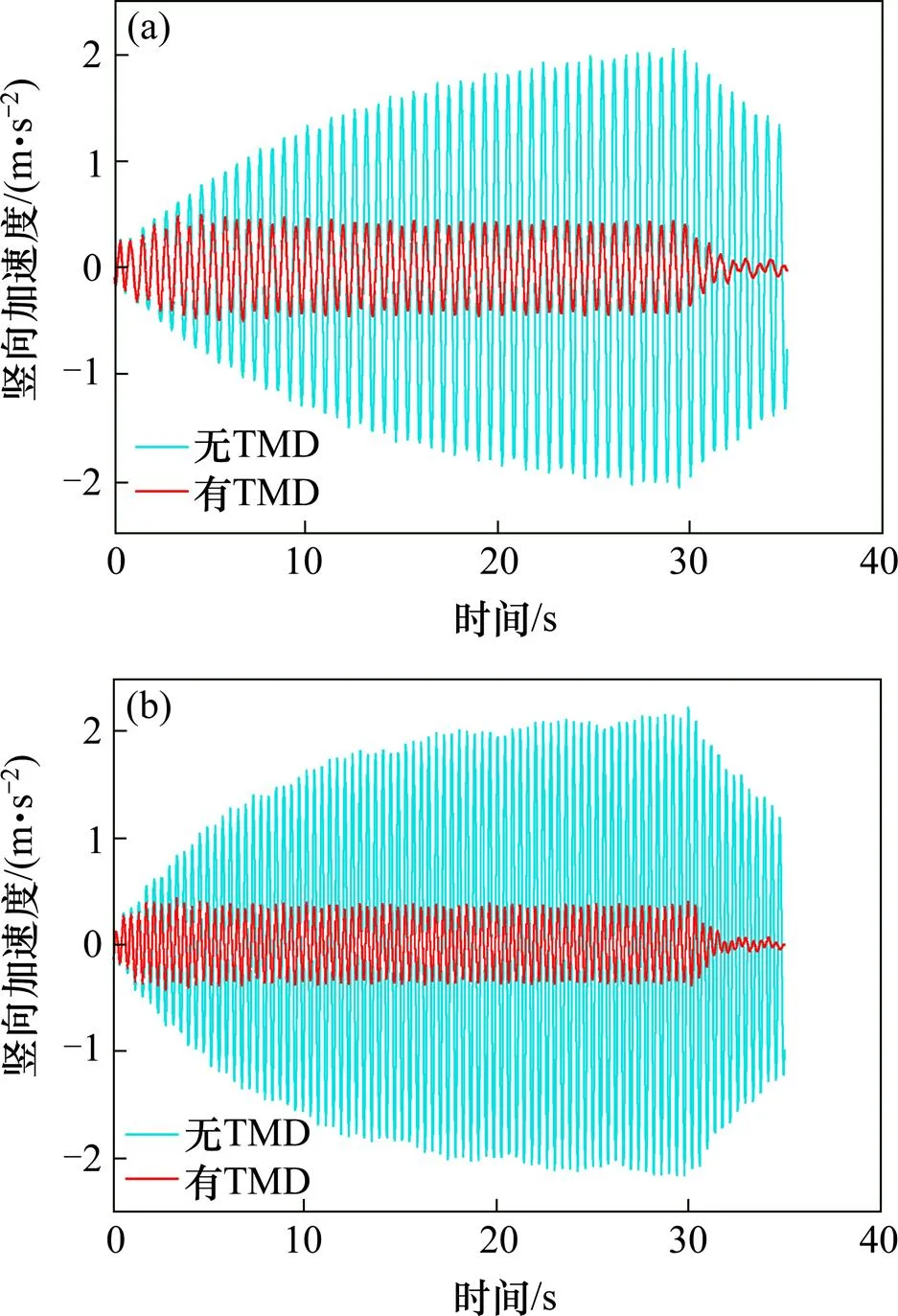
(a) 模态17跨中截面的竖向加速度； (b) 模态31下1/4截面的竖向加速度

4 结论

1) 自锚式钢箱梁人行悬索桥自振频率低，有多阶竖向及横向频率均处于行人激励荷载敏感频率范围内，很难达到我国现行规范基频大于3 Hz的要求，采用限制最大加速度响应的方法来评价人行桥人致振动的舒适度更适合现代轻型人行桥的设计。与其他规范相比，德国规范EN03-2007和ISO10137考虑了竖向和侧向振动，同时人群荷载模式可根据实际情况来调整，舒适度评价指标更为详尽，在人行桥动力设计时具有重要参考作用。

2) 以无阻尼结构TMD最优参数为初始值，针对不同模态下的TMD参数进行分析可以获得有阻尼结构TMD的最优参数。使用TMD控制结构振动响应时，TMD质量比越大，减振效果越好，但是质量比与减振率不呈线性关系，随TMD质量增大，减震率增长趋于平缓。在频率比变化时，加速度变化幅度相对较小。

3) TMD对自锚式人行悬索桥的减振效果明显，安装TMD后各工况可以更快地进入稳定状态，减振率达70.9%~81.7%，能满足规范中最好舒适度要求。自锚式人行悬索桥属于轻型大跨结构，采用TMD进行减振控制产生的附加质量较小，不影响桥梁的美观，也不会降低结构承载力，是自锚式人行悬索桥振动控制的有效方式。

[1] Clough R W. Dynamics of structures[M]. New York: McGraw-Hill, 1975.

[2] 聂建国, 陈宇, 樊健生. 步行荷载作用下单跨人行桥振动的均方根加速度反应谱法[J]. 土木工程学报, 2010, 43(9): 109−116, 130. NIE Jianguo, CHEN Yu, FAN Jiansheng. RMS acceleration response spectrum method for single-span footbridges under pedestrian load[J]. China Civil Engineering, 2010, 43(9): 109−116, 130.

[3] Den Hartog J P. Mechanical vibrations[M]. 4th ed. New York: McGraw-Hill, 1956.

[4] Brownjohn J M W, Pavic A, Omenzetter P. A spectral density approach for modeling continous vertical forces on pedestrian structures due to walking[J]. Canadian Journal of Civil Engineering, 2004, 31(1): 65−77.

[5] 法永生, 李东, 孙翠华. 人行桥随机人行荷载下的振动分析及其舒适度评价的新方法[J]. 振动与冲击, 2008(1): 119−123, 188. FA Yongsheng, LI Dong, SUN Cuihua. Vibration analysis and new comfort evaluation of pedestrian bridge under random pedestrian load[J]. Journal of Vibration and Shock, 2008(1): 119−123, 188.

[6] 陈政清, 刘光栋. 人行桥的人致振动理论与动力设计[J]. 工程力学, 2009(增2): 148−159. CHEN Zhengqing, LIU Guangdong. Pedestrian-induced vibration theory and dynamic design of footbridges[J]. Engineering Mechanics, 2009(Suppl 2): 148−159.

[7] Pedersen L, Frier C. Sensitivity of footbridge vibrations to stochastic walking parameters[J]. Journal of Sound and Vibration, 2010, 329(13): 2683−2701.

[8] 钱骥, 孙利民. 大跨径人行桥人致振动舒适性评估及减振措施[J]. 上海交通大学学报, 2011, 45(5): 677−681. QIAN Ji, SUN Limin. Comfort evaluation and vibration reduction design of long span footbridges[J]. Journal of Shanghai Jiaotong University, 2011, 45(5): 677−681.

[9] 李红利, 陈政清. 考虑荷载随机性的人行桥人致振动计算方法研究[J]. 湖南大学学报(自然科学版), 2013, 40(10): 22−31. LI Hongli, CHEN Zhengqing. A calculation method for footbridge vibration under stochastic pedestrian loading [J]. Journal of Hunan University (Natural Sciences), 2013, 40(10): 22−31.

[10] 朱俊朋, 鞠三, 徐秀丽, 等. 考虑舒适度的人行悬索桥振动控制[J]. 南京工业大学学报(自然科学版), 2013, 35(3): 56−60. ZHU Junpeng, JU San, XU Xiuli, et al. Vibration control of pedestrian suspension bridge considering human comfort[J]. Journal of Nanjin University of Technology (Natural Science Edition), 2013, 35(3): 56−60.

[11] Dallard P, Fitzpatrick A J, Flint A, et al. The London Millennium footbridge[J]. The Structural Engineer, 2001, 79(22): 17−33.

[12] Nakamura S, Kawasaki T. Lateral vibration of footbridges by synchronous walking[J]. Journal of Constructional Steel Research, 2006, 62(11): 1148−1160.

[13] 孙利民, 闫兴非. 人行桥人行激励振动及设计方法[J]. 同济大学学报(自然科学版), 2004(8): 996−999, 1060. SUN Limin, YAN Xingfei. Human walking induced footbridge vibration and its serviceability design[J]. Journal of Tongji University of Technology (Natural Science), 2004(8): 996−999, 1060.

(编辑 阳丽霞)

Study of pedestrian-induced vibration of self-anchored suspension footbridge based on TMD

ZOU Zhuo1, SONG Xuming1, LI Zhang2, TANG Mian1, HE Zeng1

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. Tianjin Design and Research Institute of Municipal Engineering, Tianjin 300051, China)

Modern long span flexible footbridges are very difficult to satisfy the requirement of current Technical Specifications of Urban Pedestrian Overcrossing and Underpass (CIJ69-95). The fundamental frequency of pedestrian bridges cannot be less than 3Hz in this specification. Comparing and analyzing current design criteria and codes for footbridges in other countries, it’s found that the method limiting dynamic response was more reasonable for the design of modern long span flexible footbridges than tuning the natural frequencies of the structure. To provide the evidence for developing the comfort evaluation standards to pedestrian-induced vibration of footbridges, this paper built the finite element model, and calculated the dynamic characteristics of a three-span steel box girder self-anchored suspension footbridge. According to EN03-2007 and ISO10137, the pedestrian load mode, acceleration response and comfort evaluation were analyzed. Taken the optimal parameters of tuned mass damper (TMD) of undamped structure as the initial values, the mass ratio and frequency ratio between TMD and this bridge were optimized and the sound vibration control method was determined. The results show that the pedestrian-induced vibration reduction ratios of this footbridge are from 70.9% to 81.7% after attached the TMD whose mass is only 1.5% of the bridge girder. The vibration response can reach the best comfort requirements of relevant specifications.

self-anchored suspension footbridge; pedestrian-induced forces; pedestrian-induced vibration; comfort evaluation; vibration control

10.19713/j.cnki.43−1423/u.2018.10.017

U44

A

1672 − 7029(2018)10 − 2574 − 09

2018−04−24

国家自然科学基金资助项目(51378503)

宋旭明(1974−)，男，湖南醴陵人，副教授，博士，从事桥梁设计理论、极限承载力研究；E−mail：ctysxm@163.com