PBL剪力键混凝土榫在特定破坏模式下的应力状态分析

赵建波，王志浩，孙允达，黄超萍，肖林



PBL剪力键混凝土榫在特定破坏模式下的应力状态分析

赵建波1，王志浩1，孙允达1，黄超萍1，肖林2

(1. 燕山大学 建筑工程与力学学院，河北 秦皇岛 066004； 2. 西南交通大学 土木工程学院，四川 成都 610031)

根据实验建立3个PBL剪力键有限元模型，结合荷载—滑移曲线，对不同破坏模式下混凝土榫的应力状态进行分析。研究结果表明：剪切破坏下混凝土榫上半圆环处于主应力相差较小的三向受压状态；压碎破坏下混凝土榫上半圆环处于主应力差值较大的三向受压状态，前两者均仅在下半圆环有拉应力出现；割裂破坏下混凝土榫主应力相差较大、三向受压区域相对较小、上半圆环与贯穿钢筋接触部分存在拉应力。可通过适当加大钢板厚度、内设横向钢筋、加强外包混凝土底座等措施使PBL剪力键发生剪切破坏，从而提高其承载力。

PBL剪力键；混凝土榫；破坏模式；应力状态；荷载—滑移曲线；承载能力

PBL剪力键又称为开孔钢板连接件，由Andra和Leonhardt于1987年提出[1]，是由开孔钢板、混凝土榫以及贯穿钢筋组成的剪力连接件[2]，具有承载能力高、延性好和疲劳性能强等优点[3]。主要用于大跨结构尤其是桥梁结构中的钢混结合段[4]，来传递2种材料间的剪力。PBL剪力键传力机理复杂，影响因素多样，计算公式多[5−6]。目前，针对PBL剪力键的研究方法主要有推出实验、模型试验和有限元分析[7]3种。已有研究成果主要以有限元分析为辅助性工具，多是以推出实验为主要方法[7−9]，通过荷载—滑移曲线研究其承载能力[10]，而试验过程未能完全反映其破坏全过程的相关应力行为[11]。大多数学者认为承载力由开孔钢板下方混凝土的抗压强度、贯穿钢筋和横向钢筋这4部分组成[12]，而钢板开孔直径、钢板厚度和混凝土的粗骨料粒径等参数对承载能力以及疲劳性能[13]也有显著影响。研究表明大多数PBL剪力键的破坏模式与混凝土榫密切相关，进而影响其承载能力[14]。混凝土榫3种破坏模式有剪切破坏、压碎破坏和割裂破坏[15]。为保证其承载力达到要求，有必要对破坏模式进行应力状态分析研究。荷载—滑移曲线是PBL剪力键承载能力的整体表现，应力状态则是PBL剪力键承载能力的局部表现，结合荷载—滑移曲线，针对特定破坏模式下的应力状态进行分析研究，有助于揭示混凝土榫的破坏过程，发现影响PBL剪力键承载能力的关键因素，找到提高PBL剪力键承载能力的有效方法。本文基于ANSYS软件，参照以往学者对于混凝土榫破坏研究而提出的推出试验试件模型[13, 16]，根据发生3种破坏模式的实验数据为依据，充分考虑接触非线性和材料非线性，建立3个PBL剪力键有限元模型。结合荷载—滑移曲线，对PBL剪力键混凝土榫在特定破坏模式下的应力状态进行分析研究，并基于破坏模式下的应力状态得到提高PBL键承载能力的方法。

1 有限元模型

1.1 模型参数

参照文献[15]中发生混凝土榫剪切破坏、压碎破坏和割裂破坏的实验数据，分别建立JQ，YS和GL 3个对应的PBL剪力键有限元模型，构造图和构造参数见图1和表1。JQ和YS模型底部的混凝土连接在一起，并设有横向加强钢筋；GL模型底部的混凝土分开，不设置横向加强钢筋。

有限元分析时为了节省计算时间，对于对称结构一般会建立1/2模型，但是本次分析所建模型的混凝土可能在对称中心出现开裂，如果在对称面施加对称约束会导致计算结果的不准确，因此本次计算将建立完整的有限元模型，如图2所示。

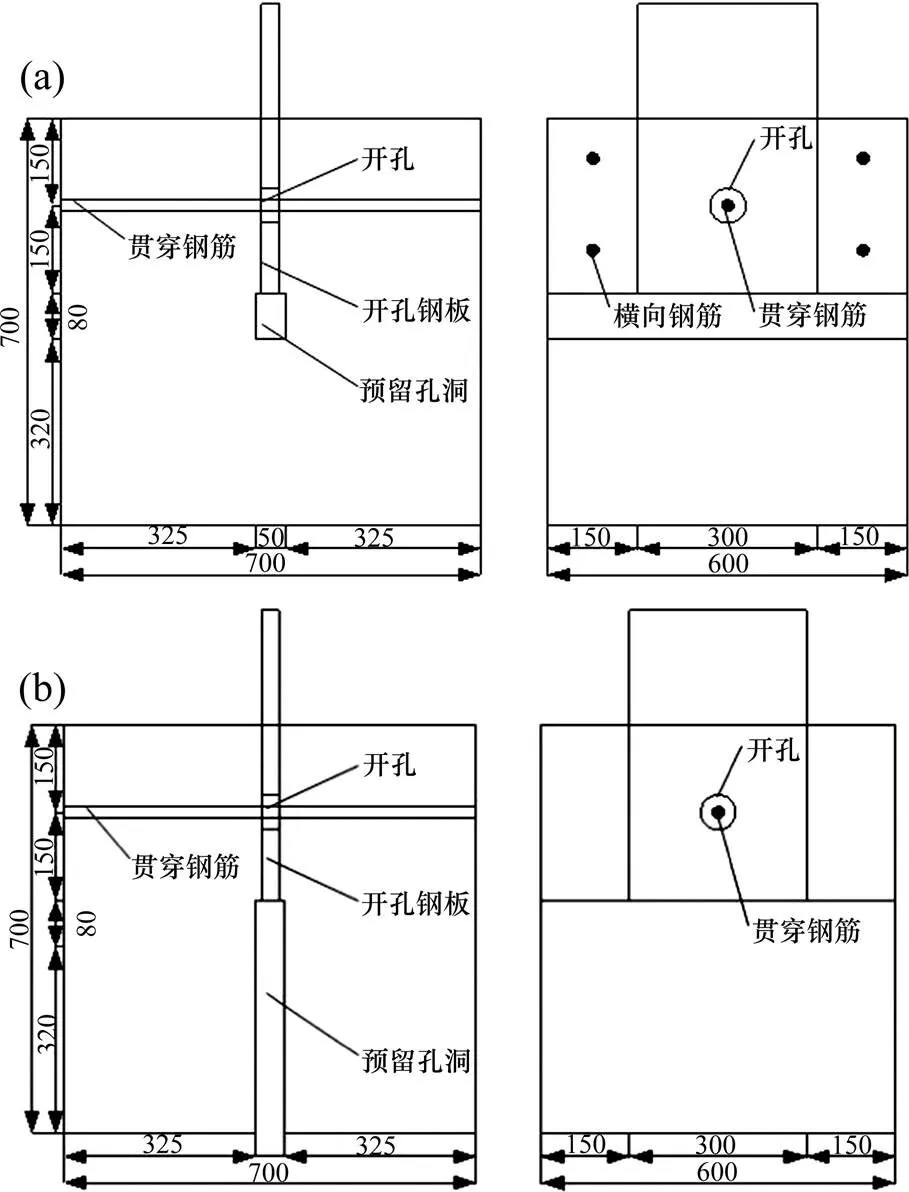
(a) JQ和YS模型；(b) GL模型

表1 模型主要参数表

注：横向钢筋与贯穿钢筋的材料类别均为HPB300，开孔钢板材料类别为Q345B

模型中各部件间的接触关系处理如下：贯穿钢筋和混凝土榫间采用绑定接触；混凝土榫上半圆环与开孔钢板间接触受压通过共用节点处理，下半圆环会与钢板发生分离故而采用可分离的接触模拟处理；混凝土榫和外包混凝土间采用绑定接触处理；开孔钢板与外包混凝土之间存在法向的相互约束和摩擦作用，开孔钢板与外包混凝土的垂直方向应用可分离的面与面接触关系来模拟，摩擦作用对于PBL剪力键的承载能力影响很小，予以忽略。

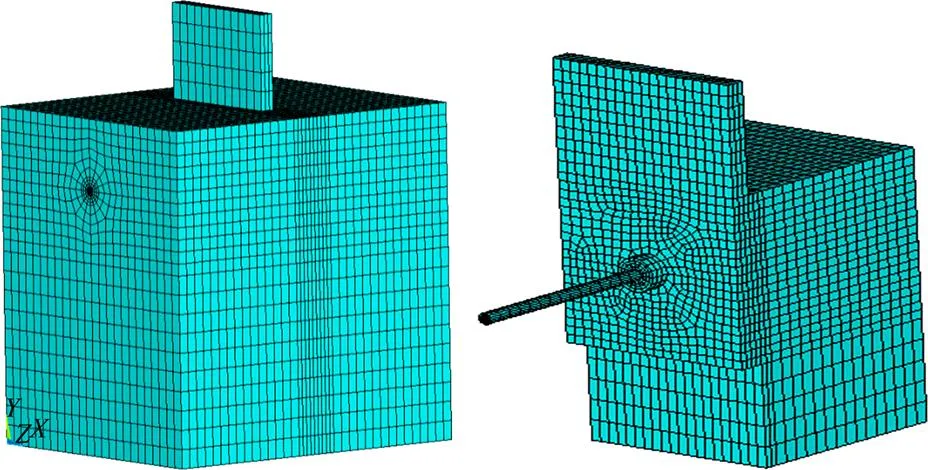
图2 PBL剪力键有限元模型

1.2 材料和单元

混凝土材料的本构关系采用MISO模型定义，由于MISO模型不能定义下降段，因此将下降部分应力应变关系采用Hongestad推荐公式确定，即用平行于轴的直线段代替。混凝土材料的强度按照《混凝土结构设计规范》(GB50010—2010)取值，抗压强度标准值ck=32.4 MPa，抗拉强度标准值tk=2.64 MPa，弹性模量0=3.45×104MPa，泊松比0=0.2。混凝土材料选用ANSYS中专门针对混凝土材料各向异性的特点所设计的SOLID65单元，该单元可充分考虑混凝土结构的压碎和开裂特点。在ANSYS中，若使用William-Warnke五参数破坏准则对混凝土同时进行开裂和压碎判断，将会造成极限荷载值偏低[17]，有限元模型会较早失效，得不到真实的极限荷载，计算较难收敛。为了得到较准确的极限荷载，本次分析关闭SOLID65单元的压碎判断。

开孔钢板和贯穿钢筋采用SOLID45单元进行模拟，利用MKIN模型来定义应力应变关系。加强钢筋用LINK8单元来模拟，用BISO模型来定义应力应变关系。在ANSYS中一般将钢材定义为理想的弹塑性材料，即上升段为一条斜率等于弹性模量的直线，达到屈服强度后应力应变曲线变为一条平行于轴的直线。本次分析贯穿钢筋和加强钢筋屈服强度均取yk1=300 MPa，开孔钢板取yk1=348 MPa，弹性模量均取1=2×105MPa，泊松比1=0.3。

2 荷载—滑移曲线分析

2.1 有限元模型的荷载—滑移曲线分析

根据有限元模型得到的荷载—滑移曲线如图3所示。随着荷载的增大其过程分为3个阶段：弹性阶段、塑性发展阶段和屈服阶段。

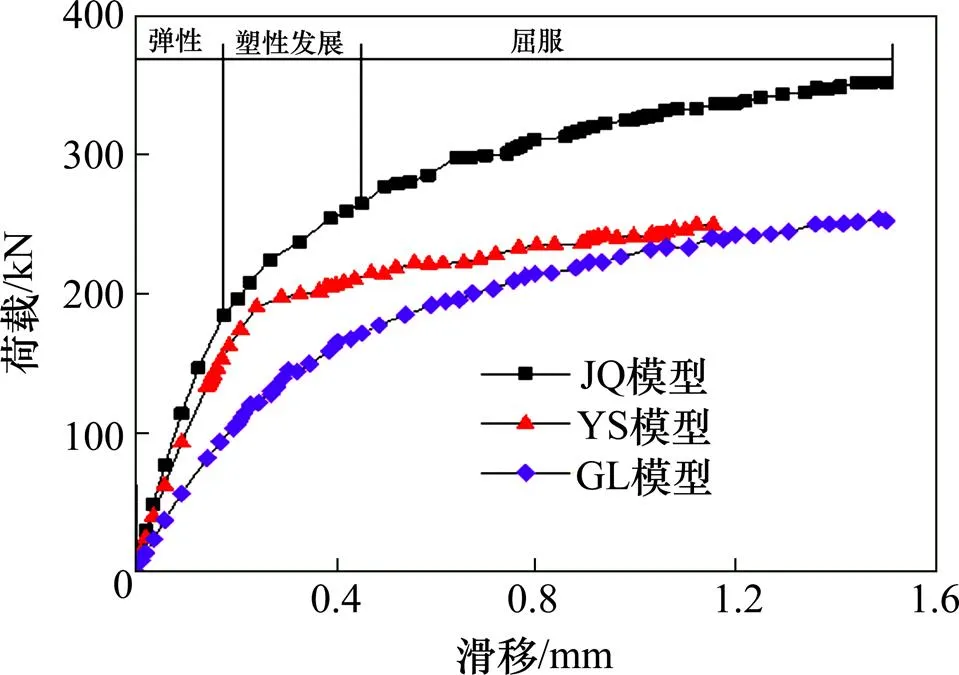
图3 基于ANSYS计算得到的荷载—滑移曲线

1) 弹性阶段：在弹性阶段，荷载与滑移量近似呈现出完全线性的关系，直线的斜率即为剪力键的抗剪刚度。此时的滑移量很小，混凝土榫还未破坏，贯穿钢筋还处于弹性阶段。从图3可以看出，在此阶段发生剪切破坏的JQ模型具有最高的抗剪刚度，其值达1 058.58 kN/mm；发生割裂破坏的GL模型的抗剪刚度最低，为574.67 kN/mm；发生压碎破坏的YS模型的抗剪刚度为928.16 kN/mm。

2) 塑性发展阶段：随着荷载的继续增加，抗剪刚度逐渐减小，此时混凝土榫逐渐破坏，剪力键的承载能力将由混凝土榫和贯穿钢筋共同提供逐渐变为主要由贯穿钢筋提供，此过程称为塑性发展阶段。

3) 屈服阶段：此时模型的非线性特征表现明显，抗剪刚度较小且下降较慢，最终抗剪刚度下降接近于0，说明此时剪力键失去了抗剪能力。PBL剪力键中混凝土榫被完全破坏，贯穿钢筋进入塑性阶段发生变形并逐渐屈服，直到最终被剪断而失去抗剪能力，此过程称之为屈服阶段。

2.2 与实验结果荷载—滑移曲线的比较分析

实验[15]中3种破坏模式下试件的荷载—滑移曲线如图4所示。试件的测试内容包括外加荷载值、开孔位置处钢板与混凝土间滑移量。实验中，荷载值由加载设备直接读取，而滑移量由高精度千分表测得。

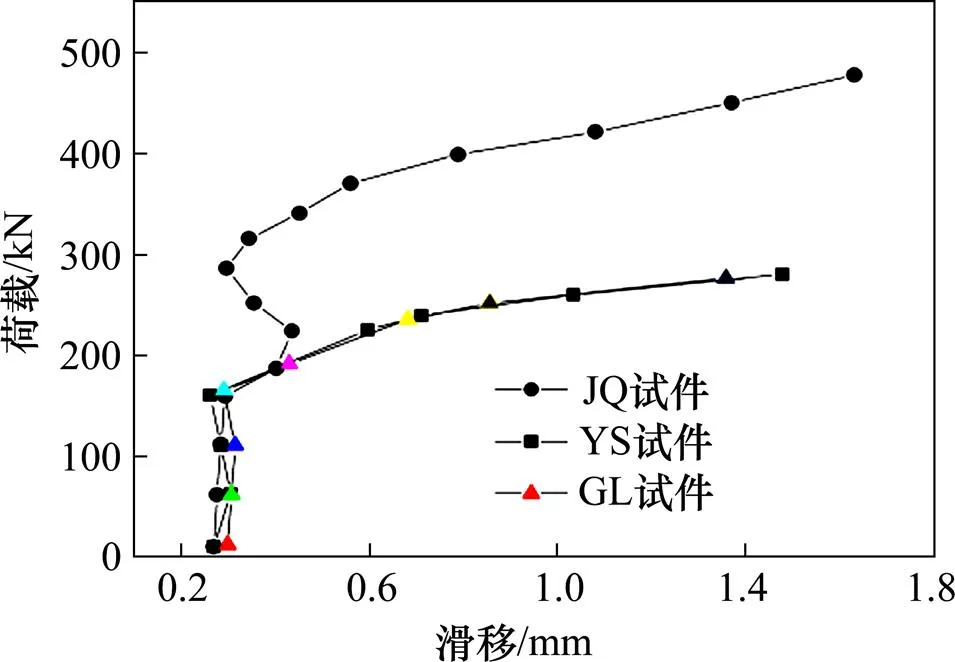
图4 实验中的荷载—滑移曲线

通过对比3种相同破坏模式的有限元模型和实验结果的荷载—滑移曲线，可以得到：

1) 当滑移量分别为0.4，0.8和1.4 mm时，有限元JQ模型对应的荷载值分别为260，311和348 kN，而实验JQ试件对应的荷载值分别为253，405和450 kN，其误差依次为2.8%，23.2%和22.7%。这主要是由于JQ试件的混凝土榫上半圆环处于高围压状态，即三向受压状态，在此高围压状态下混凝土会由脆性向塑性转变，而有限元模型中采用混凝土的MISO本构模型，该本构模型低估了高围压状态对混凝土承载力的提高，计算承载力结果较为保守，从而导致实验中此阶段的荷载值较有限元模型的荷载值大。

当滑移量分别为0.4，0.8和1.2 mm时，有限元YS模型对应的荷载值分别为207，228和250 kN，而实验YS试件对应的荷载值分别为194，248和260 kN，其误差依次为6.7%，8.1%和3.8%。YS模型和试件也处在三向受压状态，但主应力差值较大，而非处于高围压状态，所以，此破坏模式下荷载—滑移曲线得到的荷载值误差较低，曲线拟合较好。

当滑移量分别为0.4，0.8和1.4 mm时，有限元GL模型对应的荷载值分别为175，213 kN和254 kN，而实验GL试件对应的荷载值分别为187，243和265 kN，其误差依次为6.4%，12.3%和4.2%。GL模型和试件并不是处在三向受压状态，因此也不是处于高围压状态，所以此破坏模式下荷载—滑移曲线得到的荷载值误差较低，曲线拟合较好。

通过有限元模型和实验结果3种破坏模式的荷载—滑移曲线对比，发现当混凝土榫上半圆环处于高围压状态时得到的荷载误差值较大，处于非高围压状态时得到的荷载误差值较小；JQ模型和JQ试件在进入到塑性发展段后的荷载值均明显大于YS和GL模型和试件，说明混凝土榫在剪切破坏模式下承载能力比另2种破坏模式强，并在刚度衰减速度方面具有优势。剪切破坏较割裂和压碎破坏的破坏模式更具有优越性。由此可见，对于压碎破坏和割裂破坏而言，有限元模型与实验结果的荷载值误差较低，能够较好地反映出模型的准确性；对剪切破坏而言，当前商业有限元软件采用的MISO本构模型可以反映高围压状态下的应力状态，但结果较为保守。

3 混凝土榫应力状态分析

结合图3中荷载—滑移曲线特点，对混凝土榫的破坏模式及应力状态进行分析。为方便分析，将混凝土榫切割为3部分，编号为A，B和C，如图5所示。

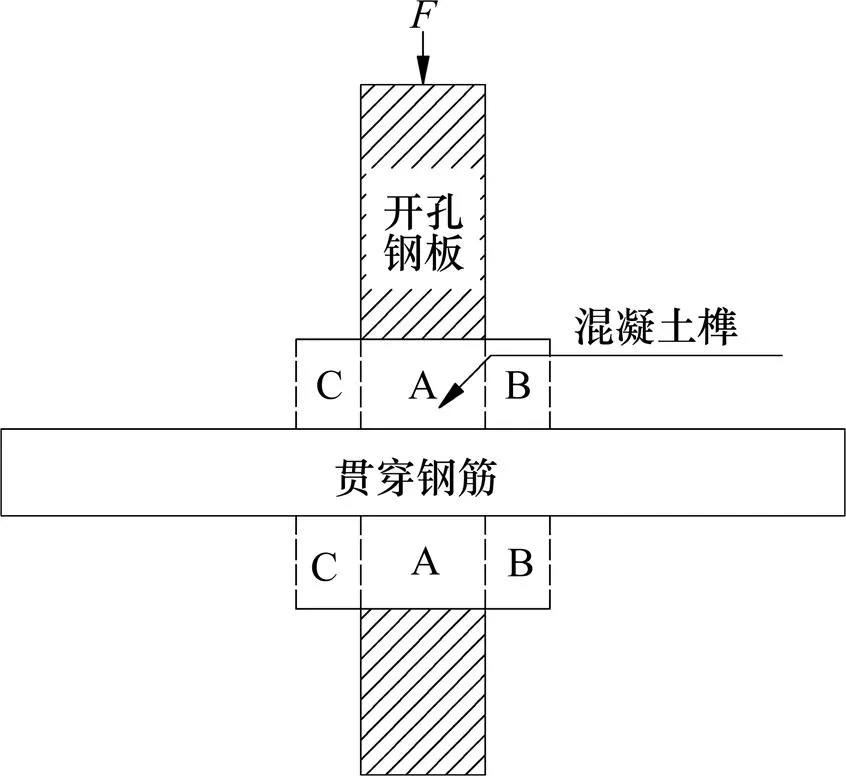
图5 混凝土榫分区示意图

3.1 混凝土榫剪切破坏过程分析

3.1.1 混凝土榫剪切破坏机理分析

模型发生混凝土榫的剪切破坏时，混凝土榫上就会形成平行于开孔钢板平面的贯通剪切面，孔内混凝土榫基本保持完好。PBL剪力键混凝土榫在荷载—滑移曲线进入非线性阶段时开始发生破坏，因此，本文在参考图3中选取JQ模型荷载为180 kN时来分析混凝土榫的应力状态。

图6为JQ模型荷载为180 kN时混凝土榫的塑性应变，从图中可以看出最大塑性应变为0.003 2，塑性应变最大的地方发生在混凝土榫与外包混凝土连接处。分析可知，模型的混凝土榫上半圆环在钢板挤压作用下产生了很大变形，但由于加强钢筋的存在，进而提供了对混凝土榫的横向约束以及沿孔洞圆周方向的孔洞约束。虽然孔洞约束作用明显要强于横向的约束，但是却能保证混凝土榫上半圆环处于三向受压状态，因此此部分混凝土榫能保存完好。与此同时由于贯穿钢筋在荷载作用下会发生弯曲导致混凝土榫下半圆环处于受拉状态，因此，对于此部分的横向钢筋也会减弱，混凝土榫在此部分将产生拉应力。故混凝土榫下半圆环处于双向受压、单向受拉状态，随着荷载的增加混凝土榫将受拉开裂并形成贯穿的剪切面。

图7为混凝土加载后期塑性应变，此时荷载为350 kN，从图中可看出，在加载后期，混凝土榫与混凝土板连接处的整个圆环已产生了很大塑性应变，最大值为0.055 5，说明混凝土榫与外包混凝土的连接已经破坏；而混凝土榫产生的应变较小，说明混凝土榫仍保存较好，此种情况与实际混凝土发生剪切破坏情形一致。

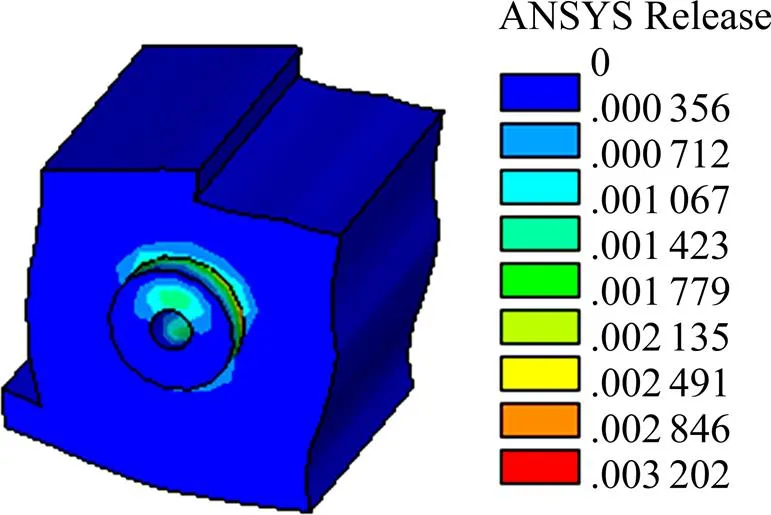
图6 JQ模型非线性阶段初期混凝土榫塑性应变

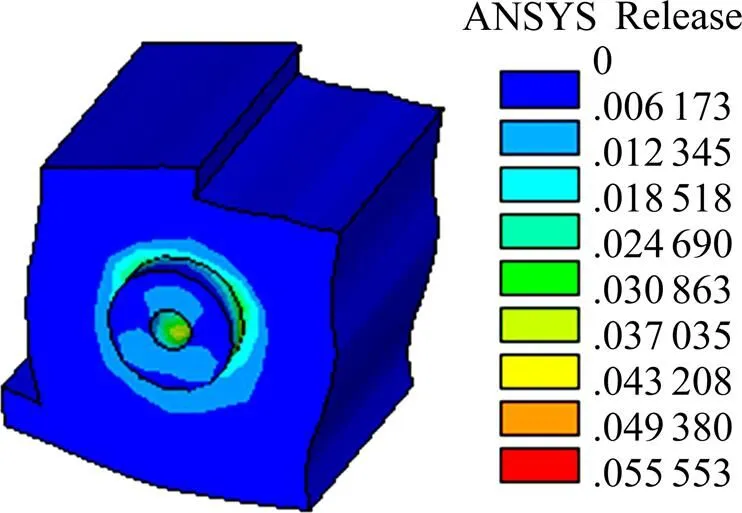
图7 JQ模型加载后期混凝土榫塑性应变

3.1.2 混凝土榫主应力状态分析

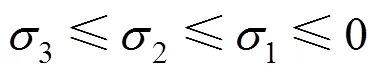
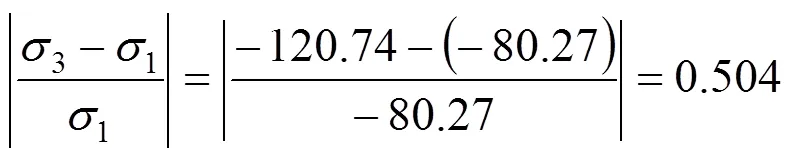
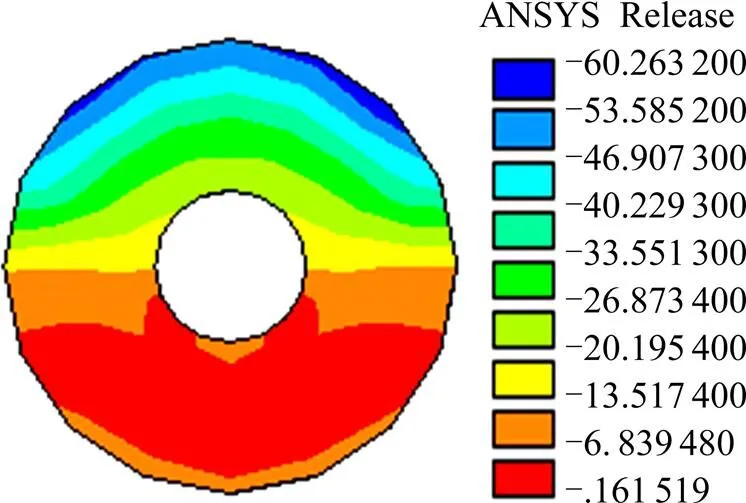
通过应力分析可知，混凝土榫发生剪切破坏的条件是提供了足够的孔洞约束，从而使混凝土榫上半圆环处于三向受压状态，并具有较强的横向约束，进而使第1主应力与第3主应力的差值较小。

单位：MPa

图8 JQ模型混凝土榫A部分第1主应力

Fig. 8 First principal stress of the concrete tenon A part in JQ model

单位：MPa

单位：MPa

为了保证其发生剪切破坏，首先保证钢板具备一定厚度，进而提供足够的孔洞约束；其次通过内设横向钢筋、加强外包混凝土底座等措施来增强混凝土榫的横向约束。

3.2 混凝土榫割裂破坏过程分析

3.2.1 混凝土榫割裂破坏机理分析

该模型的开孔钢板厚度只有12 mm，发生的是混凝土榫的割裂破坏，特点是混凝土榫在上半圆环因为贯穿钢筋的挤压作用而被压溃形成割裂破坏。同样选取荷载—滑移曲线进入非线性阶段的时刻进行分析，根据图3可知，此时的荷载值为80 kN。

图11为GL模型荷载为80 kN时混凝土榫的塑性应变图，从图中可以看出，与发生剪切破坏时的不同之处在于此时混凝土榫的最大塑性应变并不是发生在混凝土榫与外包混凝土的连接处，而是发生在孔内上半圆环。因为开孔钢板较薄，钢板孔洞对混凝土榫约束较弱，在混凝土榫上半圆环很难保证处于三向受压状态。此时混凝土榫即出现较大塑性应变，最大为1.5×10−3。此外在贯穿钢筋的挤压下，混凝土将会产生拉应力，并逐渐开裂，最终混凝土榫被割裂。

如图12所示，GL模型荷载达到250 kN时，应变的最大值为0.05，可以推测随着荷载的增加，混凝土榫在还未与外包混凝土脱离之前已经被贯穿钢筋所挤压而破坏。

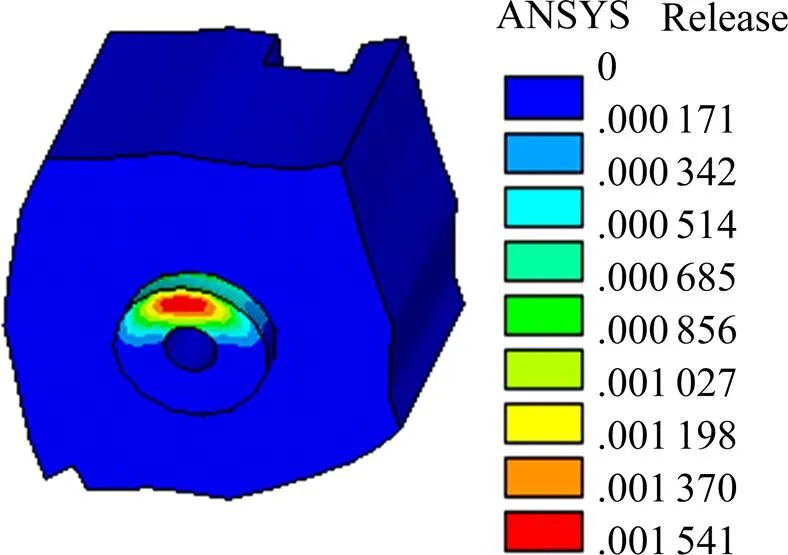
图11 GL模型非线性阶段初期混凝土榫塑性应变

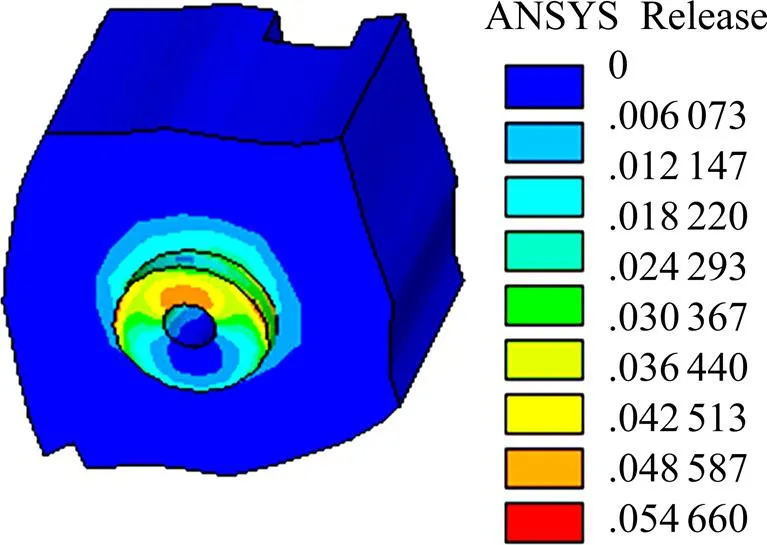
图12 GL模型加载后期混凝土塑性应变

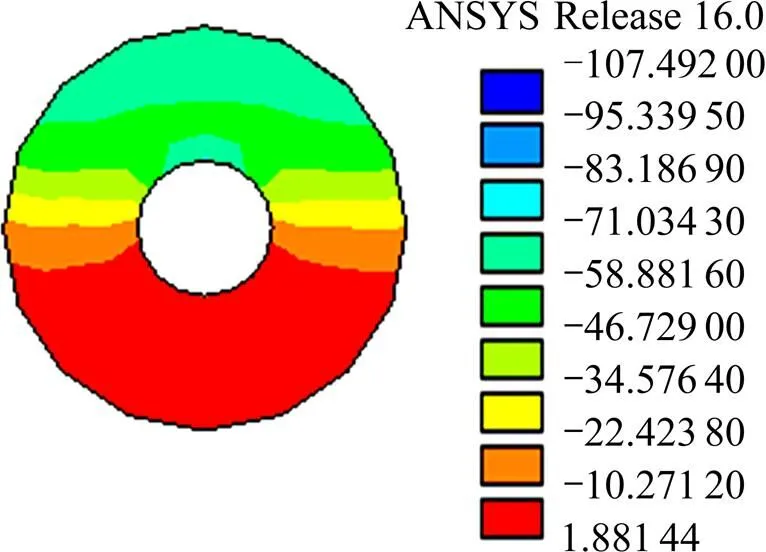
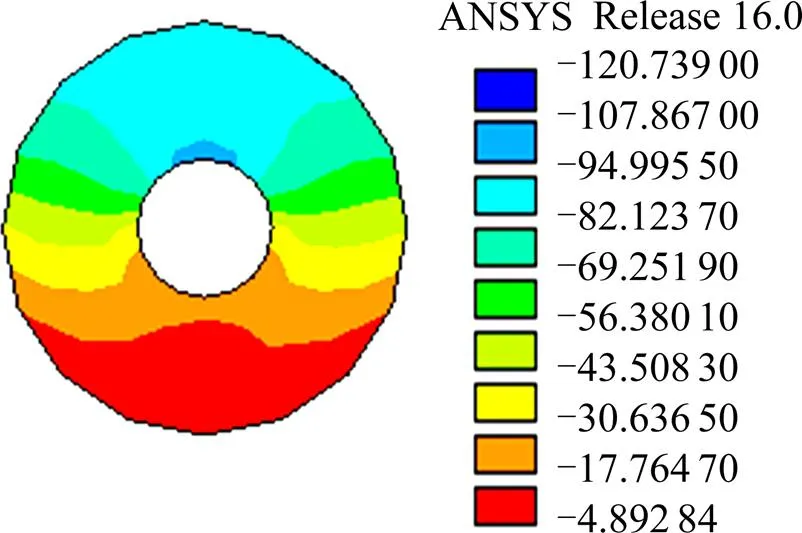
3.2.2 混凝土榫主应力状态分析

图13~15为孔内混凝土榫GL模型在荷载为80 kN时3个主应力的值，从图中可以看出，混凝土榫上半圆环处于双向受拉、单向受压状态，即混凝土榫第1主应力在上半圆环出现了拉应力，这与实验结论[15]相符。而且混凝土榫处于三向受压状态的区域相对于发生剪切破坏要小的多，第1与第3主应力相对差值为：

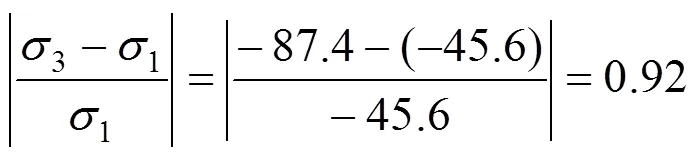
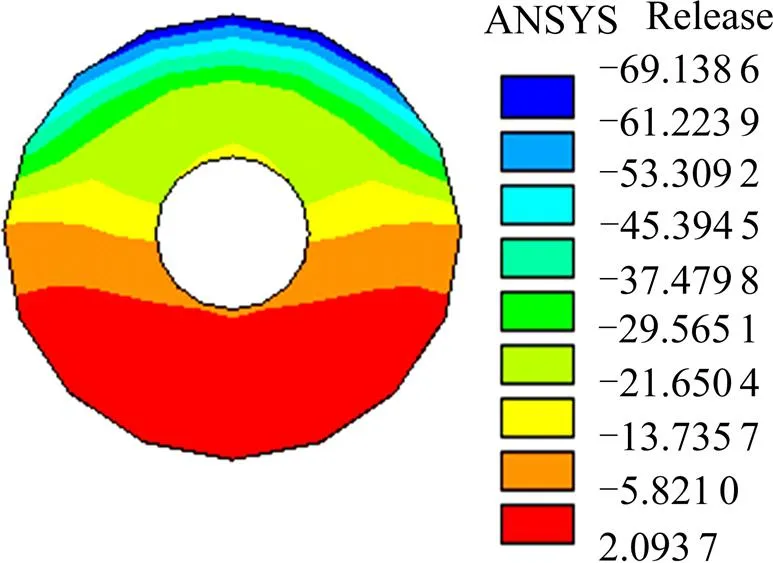
单位：MPa

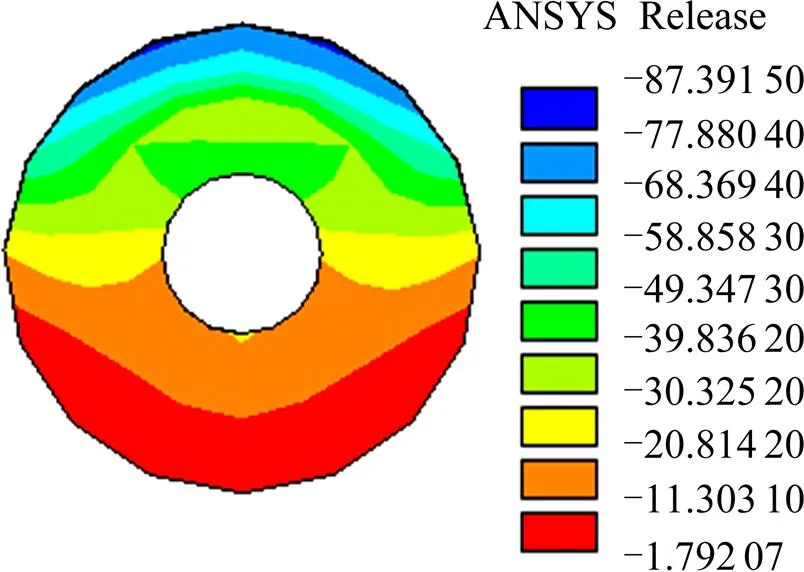
单位：MPa

通过应力分析可知，混凝土榫发生割裂破坏的条件是开孔钢板的厚度较薄，孔洞约束较弱，导致了混凝土榫的受压面积过小，局部应力过大，未能保证其混凝土榫上半圆环的三向受压状态。

在混凝土榫发生割裂破坏的情况下，混凝土榫大部分处于受拉状态下，由于混凝土抗拉强度能力弱，因此会导致PBL剪力键强度较低。因此通过使用类似于纤维混凝土等具有抗拉能力的新型混凝土，适当加大钢板厚度或者增强混凝土强度等方法来进行优化。

3.3 混凝土榫压碎破坏过程分析

3.3.1 混凝土榫压碎破坏机理分析

模型发生混凝土榫的压碎破坏时，孔内混凝土在开孔钢板两侧表面形成贯通的剪切面，孔内混凝土榫被压碎。选取荷载—滑移曲线进入非线性阶段点来分析混凝土榫的应力状态，即选取图3中YS模型荷载为150 kN时进行分析。

图16为YS模型荷载150 kN时凝土榫的应变图，从图中可以看出，混凝土榫的最大塑性应变发生在混凝土榫与外包混凝土的连接处。该模型没有设置加强钢筋，孔内混凝土榫的横向约束仅由贯穿钢筋与混凝土之间的握裹力以及外包混凝土与平台间的摩擦力提供。当开孔钢板平面内的外包混凝土开裂以后，混凝土榫横向约束较弱的缺陷就体现出来了。随着荷载增大，混凝土榫将被破坏。

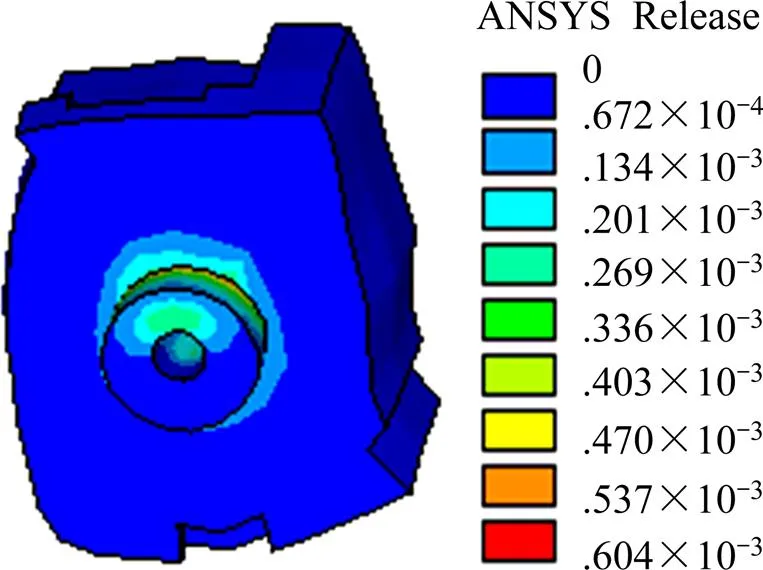
图16 YS模型非线性阶段初期混凝土榫塑性应变

图17给出了YS模型在加载的后期，荷载达到240 kN时的应变，此时孔内混凝土上半圆环产生很大塑性应变，最大应变发生在孔内与贯穿钢筋相接处，混凝土榫已经部分被压碎。

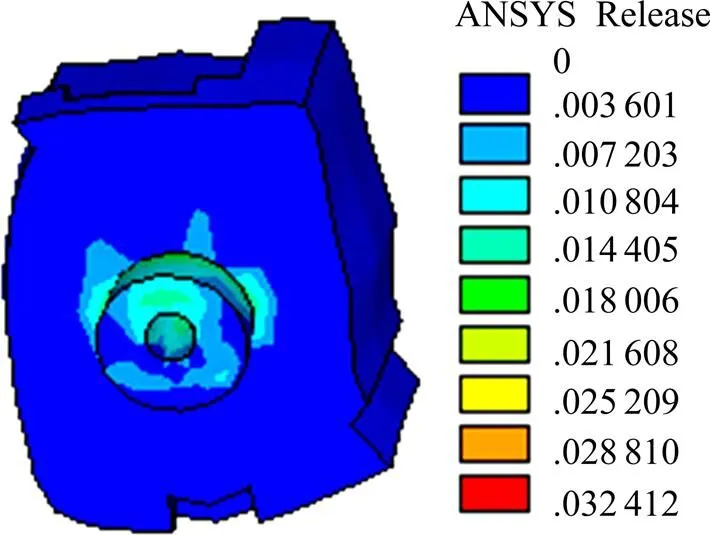
图17 YS模型加载后期混凝土塑性应变

3.3.2 混凝土榫主应力状态分析

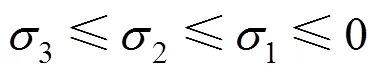
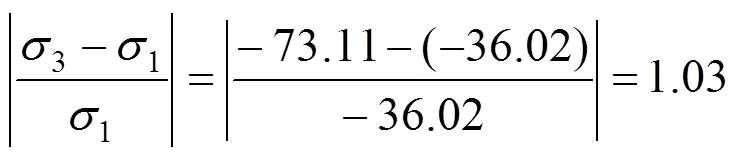
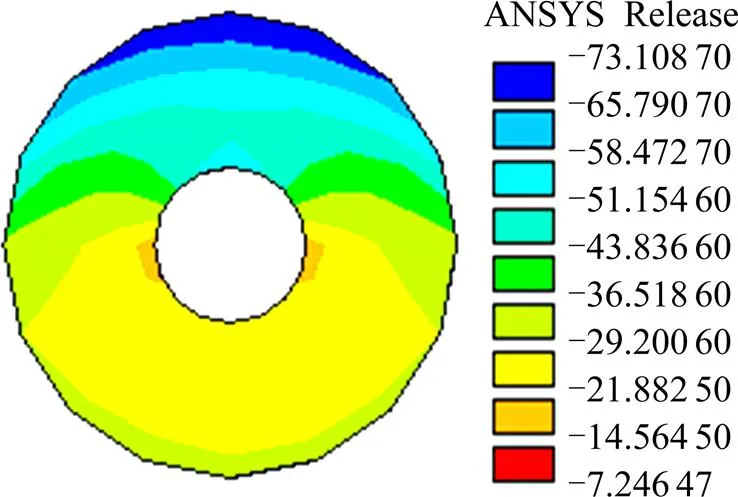
混凝土榫第1主应力在下半圆环出现了拉应力，此主应力的方向垂直于混凝土榫平面。

单位：MPa

图18 YS模型混凝土榫A部分第1主应力

Fig. 18 First principal stress of the concrete tenon a part in YS model

通过应力分析可知，混凝土榫发生压碎破坏的条件是具有足够的孔洞约束，从而使混凝土榫上半圆环处于三向受压状态；但其横向约束不足，进而第1主应力与第3主应力的差值较大。应当通过使用横向约束较强的改进型PBL剪力键等方法来减小这种应力差距。

单位：MPa

单位：MPa

4 结论

1) 通过非线性有限元仿真分析初步探明混凝土榫不同的破坏模式下的应力状态。发生割裂破坏时，开孔钢板较薄导致混凝土榫在贯穿钢筋的挤压时不能处于三向受压的状态；发生压碎破坏时，混凝土榫横向约束较弱，处于三向受压状态，但第1主应力和第3主应力差值较大；发生剪切破坏时，混凝土榫基本处于三向受压状态，此时第1主应力和第3主应力差值相对较小。

2) 混凝土榫在发生剪切破坏时PBL剪力键具有最高的抗剪刚度和承载能力，应当适当加大钢板厚度以增强孔洞约束，同时通过内设横向钢筋、加强外包混凝土底座等措施来增强混凝土榫的横向约束，从而尽量保证PBL剪力键在承载过程中出现剪切破坏模式。

3) 在特定破坏模式下，通过分析混凝土榫内部应力状态，能够为优化PBL剪力键的承载能力提供改进参考。

4) 对于剪切破坏而言，在进行有限元仿真分析时，应注意混凝土榫高围压状态对承载能力的 影响。

[1] Ahn J H, Kim S H, Jeong Y J. Shear behaviour of perfobond rib shear connector under static and cyclic loadings[J]. Magazine of Concrete Research, 2007, 60(5): 347−357.

[2] 肖林, 李小珍, 卫星, 等. PBL剪力键的疲劳性能试验研究[J]. 土木工程学报, 2015, 48(7): 101−109. XIAO Lin, LI Xiaozhen, WEI Xing, et al. Experimental study on fatigue performance of PBL shear connectors[J]. China Civil Engineering Journal, 2015, 48(7): 101−109.

[3] 曹学亮, 李法雄, 雷俊卿, 等. 基于ABAQUS的开孔板连接件抗剪承载力分析[J]. 公路交通科技, 2013, 30(11): 89−95. CAO Xueliang, LI Faxiong, LEI Junqing, et al. Analysis of Shear-capacity of perfobond shear connectors based on ABAQUS software[J]. Journal of Highway and Transportation Research and Development, 2013, 30(11): 89−95.

[4] 司秀勇. 桥梁钢混结合段力学特性理论及试验研究[D]. 秦皇岛: 燕山大学, 2013: 1−10. SI Xiuyong. Theoretical and experimental study on the mechanical properties of bridge steel mixing section[D]. Qinhuangdao: Yanshan University, 2013: 1−10.

[5] 胡建华, 侯文崎, 叶梅新. PBL剪力键承载力影响因素和计算公式研究[J]. 铁道科学与工程学报, 2007, 4(6): 12−18. HU Jianhua, HOU Wenqi, YE Meixin. Study of influence factors and formula for the bearing capacity of PBL shear connectors[J]. Journal of Railway Science and Engineering, 2007, 4(6): 12−18.

[6] 王采, 寇立亚, 胡夏闽. 钢—混凝土组合梁开孔板连接件抗剪承载力计算研究[J]. 铁道科学与工程学报, 2015, 12(4): 892−899. WANG Cai, KOU Liya, HU Xiamin. Study of formula for the bearing capacity of perfobond connectors for steel-concrete composite beams[J]. Journal of Railway Science and Engineering, 2015, 12(4): 892−899.

[7] 肖林, 卫星, 强士中. 两类PBL剪力键推出试验的对比研究[J]. 土木工程学报, 2013, 46(11): 70−80. XIAO Lin, WEI Xing, QIANG Shizhong. Comparative study on two kinds of push-out tests of PBL shear connectors[J]. China Civil Engineering Journal, 2013, 46(11): 70−80.

[8] Davies C. Small-scale push-out tests on welded stud shear connectors[J]. Concrete, 1967, 1(3): 311−316.

[9] 江祥林, 陈一馨. PBL剪力键结构极限承载力及破坏形式研究[J]. 合肥工业大学学报(自然科学版), 2014, 37(9): 1116−1121. JIANG Xianglin, CHEN Yixin. Study of ultimate bearing capacity and destruction form of PBL shear connector structure[J]. Journal of Hefei University of Technology, 2014, 37(9): 1116−1121.

[10] 汪维安, 李乔, 赵灿晖, 等. 混合结构PBL剪力键的荷载−滑移特征曲线研究[J]. 工程力学, 2015, 32(3): 57−65. WANG Wei’an, LI Qiao, ZHAO Canhui, et al. Study on load-slip characteristic curve of perfobond shear connectors in hybrid structures[J]. Engineering Mechanics, 2015, 32(3): 57−65.

[11] Ahn Jin-Hee, Lee Chan-Goo, Won Jeong-Hun. Shear resistance of the perfobond-rib shear connector depending on concrete strength and rib arrangement[J]. Journal of Constructional Steel Research, 2010(66): 1295−1307.

[12] Oguejiofor E C, Hosain M N. Numerical analysis of push-out specimens with perfobond rib connectors[J]. Computer and Structures, 1997, 62(4): 617−624.

[13] 肖林, 李小珍, 卫星, 等. PBL剪力键的疲劳性能试验研究[J]. 土木工程学报, 2015, 48(7): 93−101. XIAO Lin, LI Xiaozhen, WEI Xing, et al. Experimental study on fatigue performance of PBL shear connectors[J]. China Civil Engineering Journal, 2015, 48(7): 93−101.

[14] 黄超萍. 不同破坏模式下PBL剪力键的传力机理有限元研究[D]. 秦皇岛: 燕山大学, 2016: 1−51. HUANG Chaoping. Finite element analysis of transfer mechanism of PBL shear connectors’ concrete tenon under different failure modes[D]. Qinghuangdao: Yanshan University, 2016: 1−51.

[15] 王振海, 李乔, 赵灿晖. PBL剪力连接件破坏模式的试验研究[J]. 公路交通科技, 2012, 29(8): 68−74. WANG Zhenhai, LI Qiao, ZHAO Canhui. Experimental research on failure mode of perfobond rib shear connectors[J]. Journal of Highway and Transportation Research and Development, 2012, 29(8): 68−74.

[16] Robert W S, Henwood R J. Development and testing of a new shear connector for steel concrete composite bridge[C]// Forth International Bridge Engineering Conference, San Francisco, California, USA, 1995: 137− 145.

[17] 梅毕祥, 许明. 基于ANSYS的混凝土极限荷载影响因素分析[J]. 南昌工程学院学报, 2009, 28(1): 35−40. MEI Bixiang, XU Ming. Analysis of influence factors of concrete limit load based on ANSYS[J]. Journal of Nanchang Institute of Technology, 2009, 28(1): 35−40.

(编辑 阳丽霞)

Analysis of stress state of PBL shear connectors’ concrete tenon in specific failure mode

ZHAO Jianbo1, WANG Zhihao1, SUN Yunda1, HUANG Chaoping1, XIAO Lin2

(1. School of Architectural Engineering and Mechanics, Yanshan University, Qinhuangdao 066004, China; 2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Based on the experimental data, three finite element models of PBL shear connectors are established. Combined with load slip curve, the stress state of PBL shear connectors’ concrete tenon under different failure modes is analyzed by ANSYS. The results show that the upper half of the concrete tenon in the shear failure mode is in the three-way compression state with small difference in principal stress, and only in the lower half of the ring there is tensile stress. In the crushing failure mode, the upper part of the concrete tenon is in the three-way compression state with large difference in principal stress, and tensile stress only exists in the lower half of the ring. In the splitting failure mode, the concrete tenon has a large difference in the principal stress, and the three-way pressure region is relatively small, and tensile stress exists in the part where the upper half of the ring is in contact with the throughout reinforcement. The shear failure mode can be germinated by increasing the thickness of the steel plate, adopting transverse reinforcement and strengthening the outsourcing concrete base, so as to improve the PBL shear connectors’ bearing capacity.

PBL shear connectors; concrete tenon; failure mode; stress state; load slip curve; bearing capacity

10.19713/j.cnki.43−1423/u.2018.10.022

443.37

A

1672 − 7029(2018)10 − 2612 − 09

2017−07−21

国家青年科学基金资助项目(51308467)

赵建波(1980−)，男，河北邯郸人，副教授，博士，从事大跨度桥梁钢结构、钢混组合结构研究；E−mail：jbzhao@ysu.edu.cn