基于改进RANSAC的点云关键点匹配

赵 凯， 朱 愿， 谢 枫

(1 陆军军事交通学院， 天津 300161； 2 军事交通运输研究所， 天津 300161)

引言

随机抽样一致性(RANdom SAmple Consensus, RANSAC)算法是目前热门流行的特征点匹配算法之一[1]，该算法是由Fischler 和 Bolles 于 1981 年研发提出的一种鲁棒性模型参数估计算法[2]。由于其表现出结构简单及方法的鲁棒性高等优点，已广泛地应用于解决各个研究领域的模型参数估计问题。Chen等人[3]首次将 RANSAC 算法应用于三维点云数据的配准中，该算法在处理重叠部分较小的点云数据集时，具有一定的鲁棒性。然而，当点云配准问题中外点比例较高时，难以兼顾效率、精度和鲁棒性。为此，本文对标准RANSAC算法加以改进，提高了算法的执行性能和适应能力。

1 标准RANSAC算法

RANSAC算法是基于假设和检验的框架来实现的。首先从输入的数据点集中随机地选择一个可保证模型估计的最小数量的点集，并用该数据点集来估计模型的参数。然后，用点集中的所有数据对模型进行检验，进而确定模型的支持度、即适应该模型的数据点的数量，以此来评估该模型的正确程度。通过不断地执行假设与检验的循环，期望获得一个具有全局最优模型估计参数。

假设需要将源点云数据集U，配准到目标点云数据集V所在的坐标系下，基于RANSAC的配准算法的步骤可设计分述如下：

(1)从n对预匹配的点对{(a1,b1), (a2,b2),...,(an,bn)}中随机选取3对关键点点对作为初始匹配点对，求解位姿变换矩阵T。

(2)计算源点云中剩余n-3个关键点ai(1,2,...,n-3)经过矩阵T变换后得到的对应点Tai，并计算这些点与原先配对的n-3个关键点bi(1,2,...,n-3)之间的欧氏距离di，其计算公式如下：

di=‖bi,Tai‖

(1)

若di<ε(ε表示距离阈值)，则该关键点对(ai,bi)为内点，即正确的匹配点对，反之则为外点。

(3)比较当前内点数目，若大于当前最佳内点数Ni(设初始最佳内点数Ni为0)，则将当前变换矩阵T计作当前最佳矩阵估计，并更新最大内点数Ni值。

(4)跳转至步骤(1)，在匹配点对中重新随机抽取3组点对。

(5) 经过若干次随机抽样计算后(达到最大迭代次数或是内点数量基本保持不变)，比较各次所得的内点个数，最大内点数Ni所对应的变换矩阵T就是需要求取的两帧点云之间的位姿变换关系。

综合以上步骤，即可迭代计算出欧式变换矩阵T，从而实现源点云U到目标点云V的配准。通常情况下，RANSAC 算法可以通过不断迭代的方式来得到一组全局最优解。但是随着测试点中外点比例的增加，过程中需要的迭代次数将呈指数增长，大大地增加了计算成本。

2 改进型RANSAC算法

为了提高 RANSAC 算法的效率及性能，本文提出一种基于样本内在约束的最优RANSAC算法。该算法在随机抽样阶段，以样本之间存在的内在约束作为先验信息来引导算法的抽样过程，以此来提高算法的抽样效率；在模型检验之前增加了预检验步骤, 可以排除大部分具有明显偏差的模型, 避免不必要的模型参数检验计算；当达到停止条件退出循环后，借鉴O-RANSAC 算法[4]的思想，再依据一个更小的误差阈值, 采取逐步移除误差最大的数据的方法对准最优内点集进行提纯优化; 最后用提纯得到的最优内点集来计算模型的参数。算法的整体设计流程如图1所示。

该算法主要从3个方面对标准RANSAC算法做出改进。研究将对此展开探讨论述如下。

2.1 基于样本内在约束的随机抽样

RANSAC 算法采取独立随机方式进行抽样，没有利用数据的先验知识来引导抽样过程, 因而抽样效率较低。在点云的配准问题中，需要在两帧点云数据的重叠区域，找到至少3对对应关键点，且要求各点云中的3个关键点不能共线，才能完成刚体变换矩阵参数的估计。考虑到关键点之间的空间位置关系不会随着点云间的刚体变换而改变，因此抽样所得的最小样本集也必须满足这些约束，同时这也是正确估计模型参数的必要条件。改进RANSAC算法通过判断关键点之间的空间位置关系是否满足相应条件来引导算法的抽样过程，以此提高抽样效率。

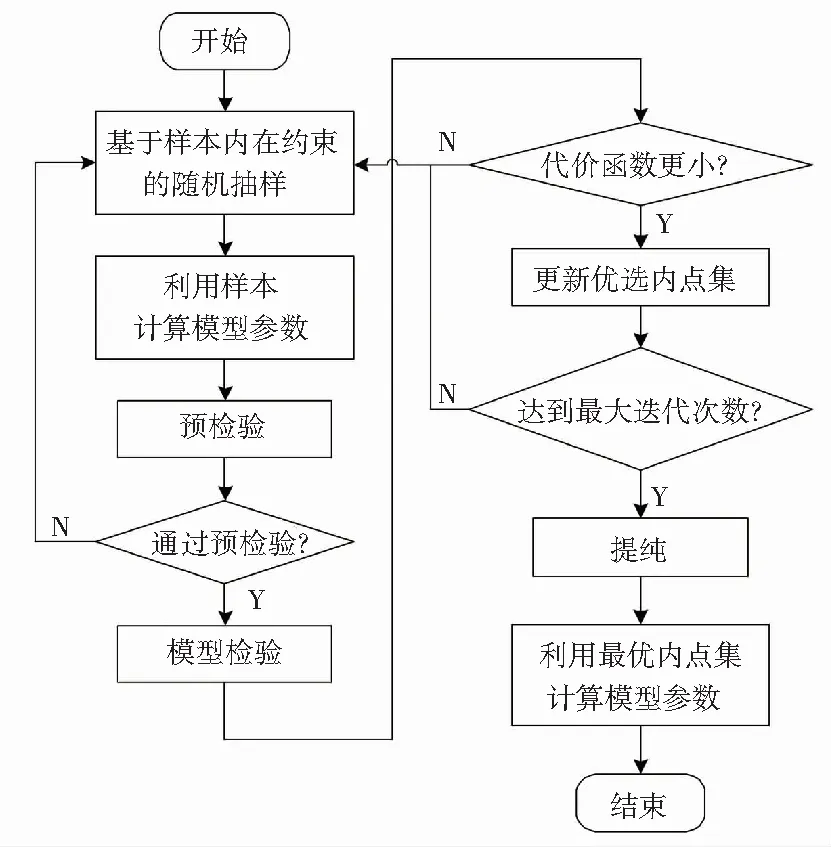
图1 改进RANSAC算法框图

假设，从待匹配集合M中抽取了3对关键点点对{(a1,b1),(a2,b2),(a3,b3)}，其中{a1,a2,a3}来自于源点云，{b1,b2,b3}分别是在目标点云中的对应点。且这3对关键点均来自两帧点云的重叠区域，那么其中的各项数值将满足以下约束：

(2)

(3)

将式(2)称为距离约束，将式(3)称为角度约束。在抽样阶段，若所抽取的样本满足这2种约束，则进行后续处理。反之，将转入重新抽样。

2.2 预检验

由于大部分模型参数都受到外点的影响，此时只需从原始数据中随机选取少量数据就可以用较少的计算代价去除大部分质量不高的模型，这就可以有效减少算法的计算时间。预检验过程的主要步骤可表述如下。

(1)从集合M中随机选取一个包含ξn对关键点的子集M′。

(2) 用M′中的所有元组对模型参数进行预检验。

(3)若M′中包含的ξn个关键点对全都符合所估计的模型参数，将通过预检验。反之，则拒绝该模型。

其中，ξ为系数，通常取值为ξ∈[0.1,0.3]。可以将ξ理解为抽样估计的模型参数所能接受的内点率。只有潜在的准确模型估计, 才能通过预检验并在数据集D上接受所有数据的检验。

2.3 准最优内点集提纯

为了对 RANSAC 算法精度进行优化，采用减小距离阈值ε的方式对准最优内点集进行提纯。在达到停止条件退出循环后，依据预先设置的距离阈值ε可以得到一个潜在的最优内点集，称其为准最优内点集。然而由于阈值ε的存在，根据准最优内点集计算得到的位姿变换矩阵T并不是最优的，该内点集中仍然包含了一些需要剔除的外点。因此可以再次采用一个较小的阈值ε′对准内点集进行提纯，从而得到最优内点集。

核心思想是：通过迭代来逐一检验并移除外点。每次迭代，利用现有模型计算全部准内点的误差, 然后从准内点集中移除一项误差最大的数据, 再利用新的准内点集计算模型参数。重复这一过程, 直到剩余内点的误差全部处于阈值ε′范围内。分析可知,这时的内点率远远高于集合M中的内点率，因此仅需要很少的迭代次数就能找到最终的最优内点集并得到最终的最优模型。

3 实验结果与分析

为了验证本文提出方法的有效性和鲁棒性，对模拟数据和真实点云数据分别进行实验，同时将本文算法与RANSAC算法的计算精度和计算耗时作以实验对比分析。采用Velodyne HDL-64E型64线激光雷达所采集的城市复杂动态环境下的三维点云数据为真实点云数据。实验平台为Intel(R) Core(TM) i7-6700 CPU @ 3.40 GHz，16 GB ARM，Ubuntu 16.04操作系统，Qt Creator 5.7开发环境，开发语言为C++。

研究仿真中首先使用IRON算法对相邻点云帧进行特征点检测，并使用匹配算法对特征点进行匹配；然后分别利用本文算法和RANSAC算法对匹配点对进行筛选，在此基础上得到了研究选用的抽样集合和参数模型；最后将欧氏适应度值(Euclidean fitness score)[5]作为点云匹配准确度的衡量指标，欧氏适应度值是参与匹配的两帧点云中各个对应点对之间欧式距离的均方差。设置预检验样本数为n=10。仿真研究的结果分析如下。

(1)2种算法计算精度对比。连续100帧点云帧间匹配的欧式适应度可如图2所示。由图2可以看出本文算法的匹配欧式适应度低于传统的RANSAC算法，即利用本文算法进行帧间配准时的精度高于使用RANSAC算法。2种配准算法的实验结果统计可见表1。实验结果取100次计算结果的平均值。内点数为正确的特征点匹配点对，内点比率为内点数占特征点数的比率。实验结果表明，本文算法在进行特征匹配点点对筛选时优于RANSAC算法，由此即验证了本文算法的计算精度高于RANSAC算法。

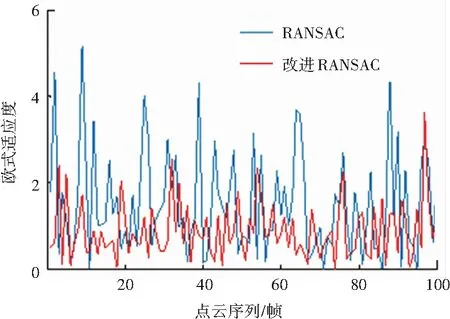
图2 2种算法计算精度对比

Fig.2Comparisonofcalculationaccuracybetweenthetwoalgorithms

表1 2种算法匹配结果对比

(2)2种算法的计算时间对比。100帧连续点云的匹配耗时，也就是2种算法的计算时间对比如图3所示。由图3可以看出本文算法所需的计算时间优于RANSAC算法，究其原因即在于本文算法在传统RANSAC算法的基础上加入了基于样本内在约束的随机抽样，可以有效地规避错误的抽样样本所带来的计算耗时；另外，预检验过程只需从原始数据中随机选取少量数据就可以用较少的计算代价排除大部分质量不高的模型，这2方面因素的综合作用就大大减少了本文改进RANSAC算法的计算时间。图4为2种算法计算时间的箱型图。由图4可以直观地看出2种算法在计算耗时上的差异，改进RANSAC算法的平均计算耗时仅为RANSAC算法的42.3%。

图3 2种算法计算时间对比

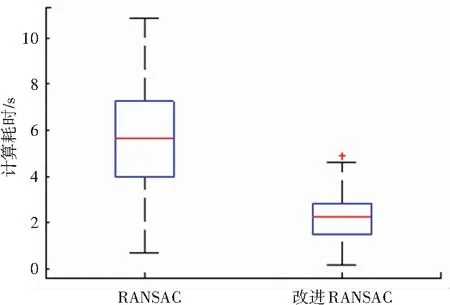
图4 计算时间箱型图

4 结束语

本文通过基于样本内在约束、预检验和准最优内点集提纯3部分设计对标准RANSAC算法加以改进，以提高算法的整体性能。基于样本内在约束的随机抽样和预检验过程在抽样及检验阶段有效地降低了计算耗时。准最优内点集提纯则是以更小的阈值限制得到最终的最优内点集，从而提高了RANSAC算法的计算精度。最后通过点云数据特征点匹配实验验证了本文算法的有效性，结果表明改进RANSAC的计算精度优于RANSAC算法，且计算时间仅为RANSAC算法的42.3%。