铥原子收敛于和偶宇称里德伯系列能级的电子关联效应∗
张典承 张颍 李晓康 贾凤东 李若虹 钟志萍3)†
1)(中国科学院大学物理科学学院,北京 100049)
2)(卑诗大学核子研究所,温哥华,不列颠哥伦比亚省,加拿大V6T 2A3)
3)(中国科学院“拓扑量子计算”卓越中心,北京 100049)
1 引 言
清楚地阐明电子-电子关联作用对原子分子的结构及其动力学过程的影响,是原子分子物理长期以来持续不断的热点课题之一.组态相互作用计算是公认的研究电子间关联效应的重要方法.里德伯原子具有高主量子数、长寿命、大极化率等特点,是研究电子关联效应的理想体系.一般而言,一个里德伯系列具有如下规则:量子数亏损近乎为常数,谱峰的强度随着主量子数n的增加急剧下降,下降规律是正比于1/n4等.而组态相互作用对里德伯能级的影响体现在破坏了里德伯能级的规则性,改变了强度分布、线形等.组态相互作用可能是两个或多个里德伯系列之间的相互作用、一个孤立态插入或者叠加在一个里德伯系列、或者连续态与里德伯系列的相互作用等.
组态相互作用引起的相干激发通道间的干涉,可以通过谱学形象地呈现,不仅深化人们对于电子间关联效应的理解,也为调控量子干涉奠定基础.电子-电子关联作用导致量子干涉效应的典型例子是Fano共振:当孤立的激发态和连续态耦合在一起时就会出现不对称的Fano线形[1],其不对称性由Fano参量q因子描述.根据Fano理论,人们提出可以用外加激光场实现量子干涉要求的能级结构,由此观测到量子干涉效应的新现象:电磁感应透明、无反转激光和相干粒子数俘获等[2,3].近年来随着阿秒激光技术的发展,人们开展吸收过程控制的研究,将洛伦兹线形转换为Fano线形或相反过程[4].基于Fano理论[1],连续和分立量子态之间强耦合引起的相位存在映射关系,意味着任何改变体系演化的现象将导致q因子的变化.Fano线形在核物理、原子物理、固态物理以及化学的分子光谱等多学科有重要应用,2017年《Nature Photonics》发表了有关综述文章[5].
基于此,选择具有复杂电子间相互作用的原子将最可能给出由于量子干涉引起的奇异谱线现象.近年来恒星光谱,特别是在化学奇特的恒星光谱中观测到大量镧系元素谱线,亟需镧系元素的谱数据,但是对大多数镧系元素而言,复杂电子组态使得光谱分析非常艰难.一般镧系元素f亚壳层未填满,导致多个价电子具有接近的电离阈值,因此阈值附近有密集的收敛于不同电离阈值的里德伯系列,是展示里德伯系列之间的相互作用、孤立态与里德伯系列作用、束缚态与连续态的耦合等电子关联效应的理想体系.最近,本课题组研究了具有三个价电子的钪原子[6]、锑原子[7]和镧系元素镥原子[8]的里德伯/自电离里德伯能级,计算结果能很好地解释实验光谱,展示了丰富的组态相互作用效应.但是钪原子、锑原子和镥原子的f亚壳层均填满,相比之下,镧系元素铥原子基态是4f13(2F◦)6s,4f亚壳层未填满,使得计算的难度增加,对这类元素里德伯能级的理论研究,不仅可以检验相对论多通道理论(RMCT)的计算精度,还将展示更加丰富的组态相互作用.
本文在多通道量子亏损理论(MQDT)[9−15]框架下,利用RMCT[16−22],计算了铥原子收敛于三个偶宇称里德伯系列.通过比较计算结果与美国国家标准与技术研究院数据[23,24],展示了两种类型的电子关联效应:1)里德伯系列之间的相互作用;2)镶嵌在一个里德伯系列中的一个孤立干扰态对该里德伯系列能级的影响.
2 理论方法
本文在MQDT框架下,利用RMCT计算铥原子和钙离子的里德伯能级.许多文献已对MQDT和RMCT理论进行了详细描述和讨论,这里仅作扼要介绍.在MQDT框架下,组态间的相互作用被描述为不同通道之间的相互作用.通道由一系列里德伯态及相应的连续态组成,这些态具有特定的总角动量、宇称以及角动量耦合方式,但有不同的能量.也就是说,某一通道中的一系列态,其原子实处于特定状态,激发电子角动量以及它与原子实角动量的耦合方式一定,而激发电子轨道能量不同.本征通道的物理图像可以理解为:在第α个本征通道中,由于作用域内较强的相互作用,使得在作用域外所有分解通道的电子径向波函数成为具有共同相移πµα的库仑驻波,在各个分解通道中的库仑驻波则以特定的权重Uiα线性叠加在一起(下角标i表示各分解通道).因此所有的本征通道能够有效地描述在作用域内复合体的动力学特性,并可用下列物理参数定量地描述:短程散射矩阵的本征值(即本征量子数亏损πµα)和其本征矢量Uiα(所有本征矢量组成正交的转换矩阵).这些物理参数,即MQDT参数,在阈值附近随能量是光滑变化的.因此对某一本征通道,只要获得有限能量点的MQDT参数,就可以得到整个通道无限个里德伯态和与之相应的连续态的物理特性,从而大大节省了计算量.
而在MQDT基础上进一步发展的RMCT,不仅考虑了有限束缚类组态的相互作用,而且考虑了无限多的里德伯态和相应的连续态的相互作用.由此可以计算有限能量点的MQDT参数,从而在MQDT框架下得到某一通道的无限里德伯态的能级.根据量子电动力学(QED),在库仑规范下,忽略Breit相互作用和其他高阶QED[25−27]修正,原子中电子所满足的狄拉克方程如下:

为残余相互作用.
根据Dirac-Slater自洽场方法(局域交换近似)得到原子的相对论性自洽势VSCF,在此基础上可求出所有束缚和连续的单电子波函数ϕa(a对于束缚和连续波函数分别代表量子数nκ和`oκ).这组单电子正交完备基函数在一定的电子排布下,经过反对称化以及适当的角动量耦合,就可构造出组态波函数,形成N电子体系的正交完备基函数.
某一能量本征态波函数Ψ(E,i)可表示成

下标j表示各电离通道.能量下限εc是该通道的里德伯态与作为通道处理的连续化高里德伯态的分界能量.通过解Lippmann-Schwinger积分方程,并利用对角化能壳K矩阵的方法,直接得到RMCT的物理参数µα、转换矩阵Uiα[16−22],从它们出发,就可对高里德伯态、自电离态及连续态作统一处理,从而计算电子的能级结构.通道原则上是无限多的,而实际计算中只能考虑有限个通道.
对于自电离谱峰的标识,根据本征通道规律,只需要计算阈值上下几个能量点的MQDT参数,就可以通过内插或外推的方法,得到阈值附近任一能量点的MQDT参数,从而可以计算里德伯态或自电离里德伯态的能级位置.对于一个实验谱中自电离共振峰的标识,本课题组完善了一套标识自电离谱峰的方法[6−8].具体做法是:一般地,如果感兴趣的自电离谱所跨能区比较小,可以认为偶极跃迁矩阵元Dα是常数,因此可以令Dα=1,计算出一个特定的本征通道谱.在通常情况下,如果组态相互作用不是很强,那么就只有一个本征通道起主要作用,通过对比实验谱和计算得到的本征通道谱,可以确定自电离峰的标识,具体说,如果实验谱峰和计算的本征通道谱峰的位置比较接近,就可以把实验谱峰标识为属于这个本征通道.但显然本征通道谱不能准确地反映某个自电离峰的峰形,尤其对于那些被强烈干扰的共振态.但是通常情况下,这样的标识方法可以满足标识自电离谱峰的要求.实际上,这样的理论方法已经成功应用于计算拥有3个价电子的钪原子[6]、锑原子[7]和镧系元素镥原子[8]的里德伯/自电离里德伯能级,计算结果与实验结果符合得很好.
3 结果与讨论
根据美国国家标准与技术研究院提供的铥原子数据[23,24],在铥原子第一电离阈值附近有3个里德伯系列,分别是收敛于第一电离阈和收敛 于 第 二 电 离 阈但美国国家标准与技术研究院不能确定相应的电子总角动量J.本文计算的通道具有的电子总角动量J=5/2,7/2和9/2,宇称为偶,标识为Jπ=(5/2)+,(7/2)+,(9/2)+.由于收敛于铥原子的一个4f电子电离的通道太多,目前计算只考虑了收敛于铥原子的一个6s电子电离的通道,即收敛于铥原子最低四个电离阈值的的通道.

图 1 里德伯系列的量子数亏损随激发能量的变化以及理论计算和实验差异(实验数据及标识来自美国国家标准与技术研究院[23,24].激发能量以铥原子基态为零点,本文所有图均采用此规定)Fig.1. Comparison of the present calculated quantum defects with the experimental data forRydberg series as the function of excitation energy.Experimental data and assignments are taken from Ref.[23,24].The zero-point energy represents the ground state of Tm,and all figures in this paper use this rule.
如图1所示,实验数据显示该里德伯系列明显受到扰动,扰动应该来自邻近的密集里德伯能级作用,扰动会改变相应能级的组态叠加系数,甚至最大叠加系数对应的通道发生变化,也即改变了谱峰的标识.在光谱上的体现是破坏了能级的规则性,使相应能级移动,也可能影响强度、峰形等.本文的计算如第二部分理论方法所言,包含了收敛于最低四个电离阈值的里德伯系列之间的相互作用.由于这四个电离阈值能级接近,因此这些里德伯系列在这段能区密集分布,相互作用比较明显.图2给出了计算的其他里德伯系列能级,选择了与美国国家标准与技术研究院[23,24]提供的里德伯系列实验数据差异最小的理论通道,即

从图2可以看出,除了实验量子数亏损跳变点49780 cm−1附近,理论与实验量子数亏损之差一般小于0.1,明显好于理论计算的里德伯系列.在实验量子数亏损跳变点49780 cm−1附近,和实验数据最接近的能级标识发生了变化,对J=5/2,7/2,9/2,分别是:

理论与实验的量子数亏损之差小于0.05.说明在研究的这段能区,里德伯系列之间的相互作用具体体现在:对角动量相 互作用为主;对角动量相 互作用为主;对角动量相 互作用为主.

图4是以J=7/2为例 (对于J=7/2,9/2,情况类似),给出了理论计算两个里德伯系列能级与美国国家标准与技术研究院提供的实 验 数 据 比较,可以看出,理论与实验的量子数亏损差异一般小于0.05,差异大的点,如50051 cm−1附近,能级标识有变化,对J=5/2,7/2,9/2,分别是:

说明在研究的这段能区,里德伯系列之间的相互作用具体体现在:对角动量J=5/2,以相互作用为主;对角动量相互作用为主;对角动量相互作用为主.

图2 理论对美国国家标准与技术研究院里德伯系列实验数据的重新标识Fig.2.The reassignment for experimental data[23,24]forRydberg series based on the present calculations.

图3 里德伯系列的量子数亏损随激发能量的变化以及理论计算和实验差异(实验数据及标识来自美国国家标准与技术研究院[23,24])Fig.3. Comparison ofthepresentcalculated quantum defects with the experimental data forRydberg series as the function of excitation energy.Experimental data and assignments are taken from Ref.[23,24].

图4 理论计算的级与美国国家标准与技术研究院提供的[23,24]实验数据比较Fig.4.Comparison of the present calculated quantum defects for and Rydberg series with the experimental data for Rydberg series as the function of excitation energy.Experimental data and assignments are taken from Ref.[23,24].

图5 里德伯系列的量子数亏损随激发能量的变化以及理论计算与实验差异(实验数据及标识来自美国国家标准与技术研究院[23,24])Fig.5. Comparison ofthepresentcalculated quantum defects with the experimental data forRydberg series as the function of excitation energy.Experimental data and assignments are taken from Ref.[23,24].
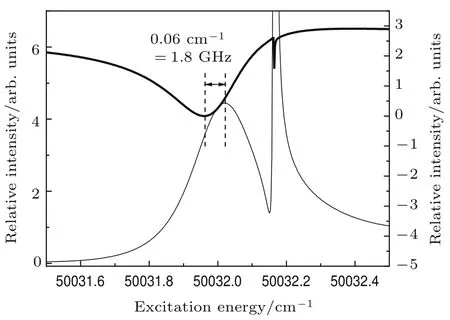
图6 组态相互作用引起的能级移动,图中细实线是计算的铥原子本征通道粗实线是计算的铥原子收敛于最低四个电离阈值所有本征通道等权(即具有偶极跃迁矩阵元Dα)叠加得到的谱Fig.6.Energy shift due to con figuration interactions.The thin line represents the present calculated eigenchannel spectrum for channelThe thick line represents the present calculated spectrum from the superposition of all eigenchannels in Jπ=(7/2)+symmetry converging to the first,second,third and fourth ionization thresholds with equal dipole matrix Dα.
美国国家标准与技术研究院提供的铥原子实验数据[23,24]还报道了收敛于第二电离阈的里德伯系列但是无法确认总角动量.与前面讨论的两个里德伯系列不同,该系列的实验量子数亏损在49900 cm−1附近跳变为1,如图5所示.说明在这个能量点附近有一个孤立束缚态与该里德伯系列强烈相互作用.导致理论与实验的量子数亏损之差高达0.6,远大于前面讨论的两个系列.表明这个干扰态属于收敛于更高电离阈值的里德伯能级.根据美国国家标准与技术研究院提供的铥原子实验数据[23,24],可以判断这个干扰态的标识是7/2.分析如下:根据美国国家标准与技术研究院[23,24]报道的铥原子能级位置是23873.207 cm−1,相应的有效量子数是1.56,而能级位于49900 cm−1,对应电离阈(阈值是67854.1 cm−1)的有效量子数是2.47.因此能级23873.207 cm−1和49900 cm−1的量子数亏损近乎相同,认定它们归属收敛于电离阈同一里德伯系列是合理的.只有角动量相同才能有相互作用,所以借助干扰态分析,可以进一步确定系列的总角动量为J=7/2.由于理论计算没有包含该干扰态的作用,理论和实验误差大是可以预期的.在图6中,定量讨论了组态相互作用导致的能级偏移,可以看到组态相互作用可以引起大约GHz左右的能级移动.
4 结 论
本文在复杂的多个价电子原子中展示了丰富的电子关联效应,在MQDT框架下,利用RMCT,计 算 了 铥 原 子 收 敛 于的三个偶宇称里德伯系列.通过将计算结果与美国国家标准与技术研究院数据进行比较,展示了两种类型的电子关联效应:1)里德伯系列之间的相互作用,导致里德伯系列的能级出现偏移,具体表现为里德伯系列的量子数亏损有一个整体的偏移;2)镶嵌在一个里德伯系列中的一个孤立的干扰态,破坏了该里德伯系列能级的规则性,具体表现为与干扰态能级位置相近的里德伯能级的量子数亏损出现大的跳变.
感谢北京计算科学研究中心高翔副研究员在本文工作中给予的讨论和帮助.

