关于大数定律若干问题的新认识
2018-10-26 05:47:52郭楠楠
安康学院学报 2018年5期
郭楠楠
(安康学院 数学与统计学院,陕西 安康 725000)
在概率论与数理统计教材中,大数定律又称大数定理,是一种描述当试验次数很大时所呈现的概率性质的定律。大数定律并不是经验规律,而是已严格证明了的定理,大数定律有广泛的实用价值。确切的说,大数定律是以确切的数学形式表达了大量重复出现的随机现象的统计规律性,即频率的稳定性和平均结果的稳定性,并讨论了它们成立的条件。但是由于直觉认识上的一些误区,许多人对大数定律有直觉上的错误认识,本文主要给出了大数定律直觉认识的一些误区,同时通过列举反例进行说明。
1 马尔科夫条件成立时,切贝谢夫大数定律不一定成立
若{ξk}服从切贝谢夫大数定律(此时Dξk≤c,ξ1,ξ2,…,ξk,…相互独立),则它一定服从马尔科大数定律,因为这时恒有从而
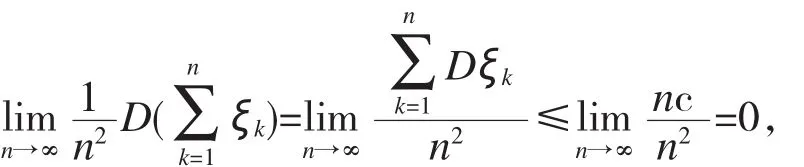
即切贝谢夫大数定律是马尔科夫定律的特例。但是,反之不一定成立。例如,设ξ1,ξ2,…,ξk,…是相互独立的随机变量序列,ξk的分布列为

从而{ξk}满足马尔科夫条件。但是,由于Dξk=Ink不恒小于某个常数,故{ξk}不服从切贝谢夫大数定律。
2 马尔科夫条件并非大数定律成立的必要条件

结合切比雪夫不等式有
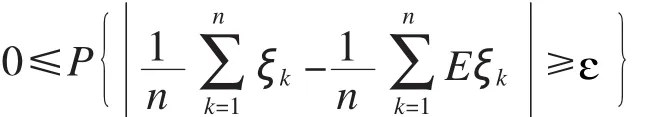

3 不满足马尔科夫条件不一定不服从强大数定律

下面证明其服从强大数定律。在此例中作


4 独立同分布不一定服从强大数定律

猜你喜欢
音乐天地(音乐创作版)(2023年4期)2023-08-10 10:35:34
数学小灵通·3-4年级(2022年12期)2022-12-23 06:09:24
有色金属(矿山部分)(2021年4期)2021-08-30 06:10:34
数学小灵通·3-4年级(2020年9期)2020-10-27 03:26:16
资源导刊(信息化测绘)(2020年5期)2020-06-22 08:37:00
少年漫画(艺术创想)(2019年6期)2019-10-12 07:35:22
汉语世界(The World of Chinese)(2019年3期)2019-07-01 02:37:48
趣味(数学)(2019年11期)2019-01-10 08:01:30
金色年华(2017年10期)2017-06-21 09:46:49
数学小灵通(1-2年级)(2017年3期)2017-04-16 04:40:28

