深刻理解“边角关系”，“高观点”下贯通思路

☉江苏省连云港市新海实验中学 宋彦波

中考试题的解法研究是很多老师的兴趣，有些考题的解法如果从初中常规思路出发往往会陷入繁杂的运算或复杂的分类讨论中，而如果对“边角关系”有更深刻的认识，往往能“删繁就简”，使得运算量大大简化，但后者又会触及所谓解法“超标”的“两难处境”，那么，这种两难处境如何应对？本文以2018年长沙中考卷第25题为例，讲解不同思路并链接同类结构问题，最后给出几点教学思考，供研讨.

一、长沙卷第25题思路优化与反思提炼

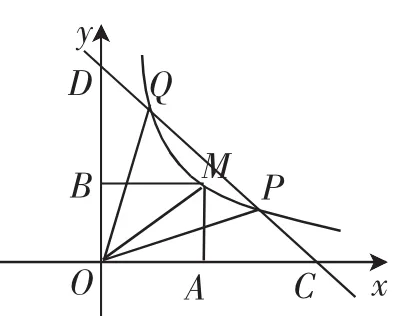
图1

考题1：（2018年湖南长沙卷，第25题，删减后）如图1，在平面直角坐标系xOy中，函数y=（x＞0）的图像经过点P（3，1）和Q（1，m），直线PQ与x轴、y轴分别交于C、D两点，点M（x，y）是该函数图像上一个动点，过点M分别作x轴和y轴的垂线，垂足分别为A、B.当1＜x＜3时，存在点M使得△OPM △OCP，求此时点M的坐标.

思路1：由函数y=（x＞0）的图像经过点P（3，1），容易求出m=3，于是结合P、Q的坐标可求出直线PQ的解析式为y=-x+4.相应地，点C（4，0）、D（0，4），即△COD是等腰直三角形，以上都可看作一些解题准备工作.

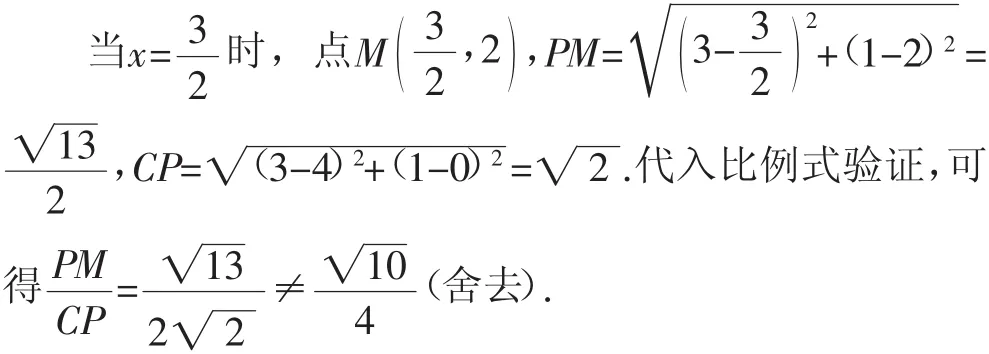
思路2：在上面一些准备工作之后，由△OPM △OCP，可确认∠MOP=∠POC.结合点P（3，1），可得tan∠MOP=tan∠POC=，可以发现tan∠MOA=tan2∠POC，若能求出tan2∠POC的值就可恰当设出M点的坐标，代入解析式得出方程.接下来分图形攻克这个难点.如图2，在线段OH上取一点G（作OP的垂直平分线交OH于点G），使GP=GO，这样可在Rt△PGH中利用勾股定理解出直角三角形PGH的三边之比为3∶4∶5，从而可得tan∠PGH=，也就是tan2∠POC=，即tan∠MOA=.可设点M（4k，3k），代入y=，解出k=，即点M（ 2，）.

思路3：由直线y=-x+4可带来∠OCD=45°，根据相似得对应角∠MPO=∠OCD=45°，抓住这个45°角作为突破口，设法求出直线PM的解析式，与曲线解析式联立也可解出交点M的坐标.接下来重点攻克直PM的解析式.

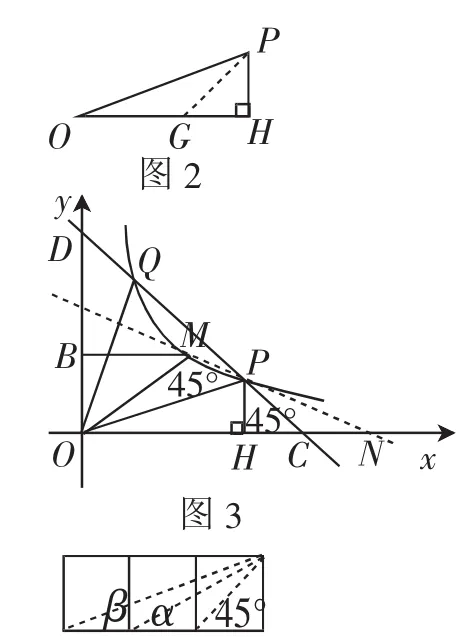
图4

如图3，设直线PM与x轴交于点N，由外角性质得∠POH+∠PNH=∠MPO=45°，tan∠POH=，可得tan∠PNH=（这一步演算可利用图4这个基本图形来获取）.

这样结合P（3，1），可得N（5，0），于是求出直线PM的解析式为y=-x+.将其与曲线的解析式联立，可解出M（ 2，）.

解后小结：利用高中两角和的三角公式tan（α+β）=，可以演算推导出如下性质：

性质1：若tanα=，则tan2α=.

性质2：若tanβ=，则tan2β=.

性质3：若tanα=，tanβ=，则α+β=45°（.特别是，这里 的三个条件可以变换组合“，知二推一”，比如，若tanα=，α+β=45°，则tanβ=；若tanβ=，α+β=45°，则tanα=)

本题中一些较为复杂的比例关系，可以通过上述性质一眼洞察，节省很多时间，解题教学时可以向优秀学生进行补充、拓展与渗透.

二、同类解题策略的考题链接

考题2：（2018年江苏淮安，第27题，有删减）如图5，在平面直角坐标系中，一次函数y=-x+4的图像与x轴、y轴分别交于A、B两点.动点P从点A出发，在线段AO上以每秒3个单位长度的速度向点O作匀速运动，到达点O停止运动.点A关于点P的对称点为点Q，以线段PQ为边向上作正方形PQMN.设运动时间为x秒.若正方形PQMN对角线的交点为T，探究运动过程中OT+PT是否存在最小值，并说明理由.

思路解析：容易求出点A（6，0）、B（0，4），即OA=6.

如图6，结合四边形PNMQ是正方形，有PT=TN，所以待分析的OT+PT可转化为OT+TN.

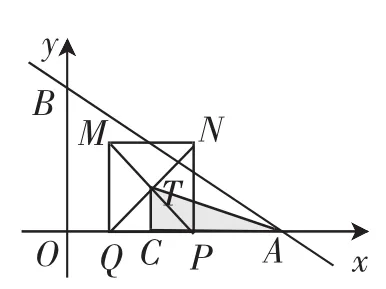
图5

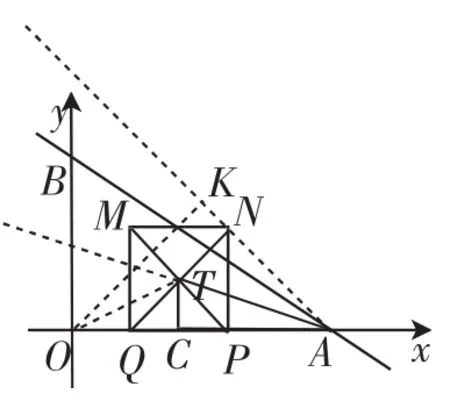
图6

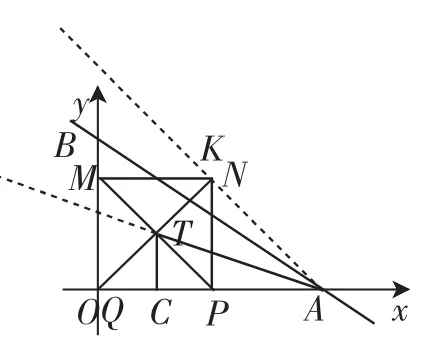
图7

再结合正方形PNMQ的边长PN=AP，连接AN，所以∠NAP=45°，即点N在直线y=-x+6上运动.

所以，当O、T、N三点在同一直线上，即ON⊥直线AN时（∠TBO=45°），OT+PT最短，此时，Q与O重合（如图7），OT+PT=OT+TN=OA·cos45°=3.

解后小结：不只是上面发现的点N在直线y=-x+6上，点T的运动轨迹也在一条直线上，如图6，容易求出即tan∠TAC=，于是T点的运动轨迹是直线y=-x+2.由考题1解后小结的一些性质也容易确认图6中tan∠TAN=.这些都符合“性质3：若tanα=，tanβ=，则α+β=45°”.

三、关于解题教学的思考

1.较难问题尽量从不同角度贯通思路

近年来，不少地区的中考把关题从初中角度来求解，往往都会陷入较难的处境，或者运算量太大，过于繁杂，考生在考场中如果不想“隐性失分”，多会选择放弃.而不少擅长解题研究的老师却能贯通很多思路，其中有些思路往往涉及高中视角（所谓“高观点视角”），然而考生却缺少这样的高观点视角，所以往往能从不同角度贯通思路.这给我们的解题教学提出了较高的要求，这就是说，在平时的解题教学过程中，如果遇到这类较难题，还是要适当向学生渗透、推介高中解法与思路，至少一些优秀学生是可以跟进思考的.当然，这也是为优秀学生“打开一扇窗”的开放式教学的追求.

2.加强同类问题的链接，促进深刻理解

《中学数学（下）》近年来发表了不少解题教学方面的课例文章，其中有一些课例都突出了同类问题的链接，或者同类问题的变式再练，这给我们很大的启发，在实践教学中，也进行了类似的训练，有效提升了教学效果.当然，同类问题的跟进关键在问题结构的相近，或者解题策略的趋同，这里往往要从形似走向神似，即多多链接“形异质同”（罗增儒教授语）的同类问题更加重要.这样可以促进学生对一类问题的“深刻理解”（这里的深刻理解，也就是马立平博士指出的追求数学知识理解的深度、广度与贯通度），练就一双“火眼金睛”，以便在今后再遇到类似问题时，可以识别并恰当转化、快速实现思路贯通.