命题热点追踪：韦达定理的隐性考查——以某市三道把关题为例

☉江苏省海门市首开东洲初级中学 夏冬平

我们知道，《义务教育数学课程标准（2011年版）》对一元二次方程的教学提出了明确而细致的要求，特别是对一元二次方程根与系数的关系（本文以下简称“韦达定理”）给出了“选学内容”的规定，按要求，“选学内容”不得列入中考.然而从数学能力的可持续发展上看，韦达定理确实关乎后续很多内容的学习，在高中阶段韦达定理也有着广泛的应用，所以全国很多地区的中考命题虽然不再“明考”韦达定理，但是“暗考”（即隐性考查）韦达定理的命题现象一直是公开的秘密.所以很多地区的师生，无论是新授课教学还是在中考备考过程中，都没有放弃对韦达定理的教学与要求.那么隐性考查韦达定理都会有怎样的方式？又该如何应对这类考题的思路突破？本文以某市2018年中考卷为例，选取该卷选择题、填空题、解答题的最后一题，从运用韦达定理的视角贯通思路，实现求解，最后提出一些教学建议，供研讨.

一、从韦达定理视角看把关题的思路突破

考题1：已知关于x的一元二次方程（a+1）x2+2bx+（a+1）=0有两个相等的实数根，下列判断正确的是（ ）.

A.1一定不是关于x的方程x2+bx+a=0的根

B.0一定不是关于x的方程x2+bx+a=0的根

C.1和-1都是关于x的方程x2+bx+a=0的根

D.1和-1不都是关于x的方程x2+bx+a=0的根

思路讲解：由一元二次方程的定义知a+1≠0.

由方程（a+1）x2+2bx+（a+1）=0有两个相等的实数根，得判别式Δ=（2b）2-4（a+1）（a+1）=0，则a-b+1=0 ①，或a+b+1=0 ②.

结合a+1≠0，可得b≠0 ③.

逐个分析4个选项：

对于选项A，把x=1代入方程x2+bx+a=0，得a+b+1=0，符合①式，故选项A错误；

对于选项B，把x=0代入方程x2+bx+a=0，得a=0，代入原方程，符合题意，故选项B错误；

对于选项C，若1和-1都是关于x的方程x2+bx+a=0的根，由韦达定理得b=1+（-1）=0，这与③式矛盾，故选项C错误；

对于选项D，把1和-1分别代入方程x2+bx+a=0，可得1+b+a=0，1-b+a=0，符合①式和②式，这里“不都是”对应着上面“或”的关系，所以选项D成立.

考题2：如图1，直线y=x+m与双曲线y=交于A、B两点，BC∥x轴，AC∥y轴，则△ABC面积的最小值是_______.

网传解答1：当AB过原点时，AB最小，则△ABC的面积最小，最小值为6.

网传解答2：当m=0时，△ABC面积的值最小，此时a=b.设点A的坐标为（a，b），则ab=3，B（-b，-a），C（a，-a），于是AC=2b，BC=2a，则△ABC的面积的最小值是：AC×BC=×2a×2b=2ab=2×3=6.

解法改进：上面两种“网传解答”虽然解法简洁，但是直觉成分多，理性分析少.解法主要不足是“当AB过原点时，AB最小”属于直观判断，缺少演算解释.以下给出这方面的解释：

因为A、B是直线与曲线的两个交点，则它们的横坐标a和b可视为方程x2+mx-3=0的两个实数根.

由韦达定理有：a+b=-m ①，ab=-3 ②.

由直线y=x+m的斜率为1，可确认△ABC是等腰直角三角形.

AC=BC=a-b.

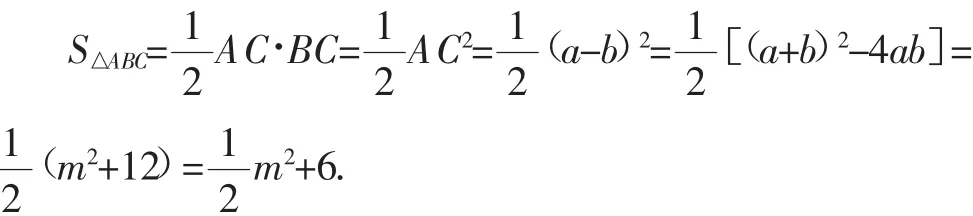
这样就有力解释了当m=0时，△ABC的面积有最小值6.

考题3：已知抛物线y=ax2+bx+c过点A（0，2），且抛物线上任意不同两点M（x1，y1）、N（x2，y2）都满足：当x1＜x2＜0时，（x1-x2）（y1-y2）＞0；当0＜x1＜x2时，（x1-x2）（y1-y2）＜0.以原点O为圆心、OA为半径的圆与抛物线的另两个交点为B、C，且B在C的左侧，△ABC有一个内角为60°.若MN与直线y=-2x平行，且M、N位于直线BC的两侧，y1＞y2，求证：BC平分∠MBN.

思路讲解：根据题意，先画出草图分析，如图2.

关键步骤之一：求出抛物线的解析式.

因为抛物线过点A（0，2），所以c=2.

已知条件“当x1＜x2＜0时，（x1-x2）（y1-y2）＞0；当0＜x1＜x2时，（x1-x2）（y1-y2）＜0”，结合二次函数的增减性，可解读出：当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而减小.这样可推定、确认抛物线的对称轴为y轴且开口向下，即b=0.

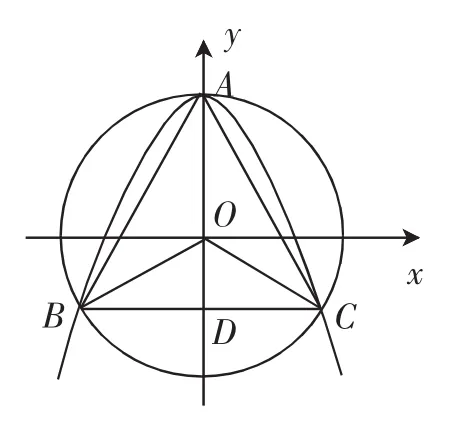
图2

接下来，由以“O为圆心、OA为半径的圆与抛物线交于另两点B、C”，容易确定△ABC是等腰三角形.再根据条件“△ABC有一个内角为60°”，可得△ABC为等边三角形.又OC=OA=2，可求出点B的坐标为（-，-1）.

将点B的坐标代入y=ax2+2，可得a=-1，所以抛物线的解析式为y=-x2+2.

关键步骤之二：证出tan∠MBC=tan∠NBC.

构造图3，作ME⊥BC于E点，NF⊥BC于F点.

设点M（x1，-x12+2）、N（x2，-x22+2）.

图3

根据韦达定理，可得x1+x2=2.

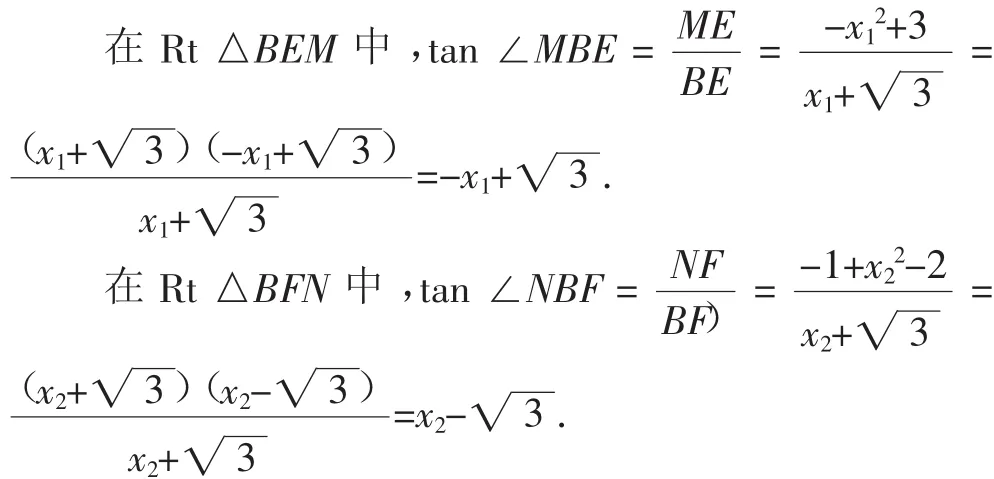
到此，若能分析出-x1+=x2-即贯通思路.而由韦达定理得出的x1+x2=2，恰好提供了这个桥梁作用.于是tan∠MBE=tan∠NBF，所以∠MBE=∠NBF，即BC平分∠MBN.

二、关于韦达定理的教学建议

1.从数学的逻辑连贯来看，韦达定理的新授课教学不宜弱化

数学各个分支学科或知识模块都具有逻辑连贯、层层递进、前后呼应的学科特点.就一元二次方程来看，从直接开方出发到配方法解一元二次方程，再演算推导出求根公式，在此过程中对根的判别式进行了研究，而通过对大量一元二次方程两个实数根的观察发现了根与系数的关系，并且可以给出证明，也就是韦达定理.这样来看，就是新授课期间也不宜对韦达定理进行弱化，这不只是数学知识的增删，而是破坏了一元二次方程整章知识的系统性、逻辑性.以笔者所见的教学现实，初三新授课期间，没有哪个老师真的把韦达定理弱化为简单介绍，而是都安排了不止一个课时的教学时间.另外，高中阶段对二次函数的学习将更加系统和深入，与韦达定理高度关联，这也决定了很多学校在新授课和复习期间都没有放松对其教学和考查的要求.

2.从命题的现实引领来看，帮助学生识别韦达定理隐性考查

如本文开篇所指出的那样，从各地命题现实来看，不少地区是以填空题或选择题的形式明考根与系数的关系，如果不掌握韦达定理，则绕着用求根公式或其他思路会耗时费力；而有些地区就会在全卷把关题位置上设置隐性考查的方式.从这种现实引领来看，在隐性考查韦达定理的解题教学时，除了常规思路要讲，还可引导学生从韦达定理的视角贯通思路，加深对韦达定理的理解.特别是，在使用韦达定理解决类似上面考题3的过程中，还要在讲评或解后回顾阶段，引导学生体会“数形结合”的解题策略，也就是体会比例式之间的数形对应关系.