基于MATLAB悬臂梁扰度分析

范玲玲，乐腾胜，童智能，项炳泉，张金钟

（1.南昌市京东学校，江西 南昌 330029；2.安徽省建筑科学研究设计院，安徽 合肥 230001；3.江西科技师范大学建筑工程学院，江西 南昌 330013）

1 引言

数学建模就是构造数学模型的过程，即用数学的语言-公式、符号、图表等刻画和描述一个实际问题，然后经过数学的处理-计算、迭代等得到定量的结果，以供人们做分析、预报、决策和控制[1]。随着计算机广泛使用与科学技术迅速发展，科学计算已是科学研究、工程设计中的一个重要的手段。合理的利用MATLAB数学软件来辅助数学演算和绘图，已成为与理论分析、科学实验并驾齐驱的科学研究方法[2～5]。悬臂梁在各种荷载及不同支撑下的扰度分析是工民建中常见的问题，主要涉及到了常微分方程初值问题的数值求解。对于一般的初值问题，通常采用改进的Euler公式，就能保证二阶精度[6-7]。如果方程右端项f（x，y）足够光滑，计算精度较高，经典四阶RK方法是不错的方法，这一点在分析悬臂梁的扰度问题中得到了很好的应用[8-9]。

本文针对悬臂梁的扰度随着梁的长度的变化而变化，在MATLAB中运用经典四阶RK公式计算，作出悬臂梁扰度图（z-y图），确定出悬臂梁中扰度最大的位置以及求出相对应的最大扰度近似解，并与挠度微分方程计算得出的精确解相对比，验证了运用MATLAB软件近似计算悬臂梁扰度的可行性，促进了悬臂梁扰度计算的研究与分析。

2 经典四阶龙格-库塔算法的介绍

经典龙格-库塔（RK）方法是一种在工程上应用广泛的高精度单步算法。由于此算法精度高，采取措施对误差进行抑制，所以其实现原理也较复杂。同Euler等算法一样，该算法也是构建在数学支持的基础之上的。对于一阶精度的欧拉公式有：

当用点Xn处的率近似值K1与右端点Xn+1处的斜率K2的算术平均值作为平均斜率K*的近似值，那么就会得到二阶精度的改进欧拉公式：

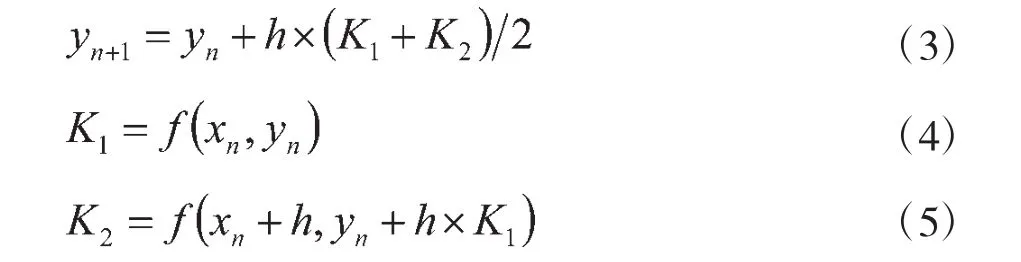
依次类推，如果在区间[Xn，Xn+1]内多预估几个点上的斜率值K1、K2、……Km，并用他们的加权平均数作为平均斜率K*的近似值，显然能构造出具有很高精度的高阶计算公式。经数学推导、求解，可以得出四阶龙格－库塔公式，也就是在工程中应用广泛的经典四阶龙格－库塔算法[10]：

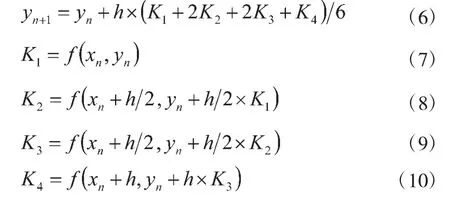
3 问题描述

如图1所示的一段被嵌入墙内的悬臂梁，在固定点A，位移y和斜度dz皆为零。设梁是一根均匀细杆，其长度为L。梁关于垂直方向y的扰度满足微分方程：

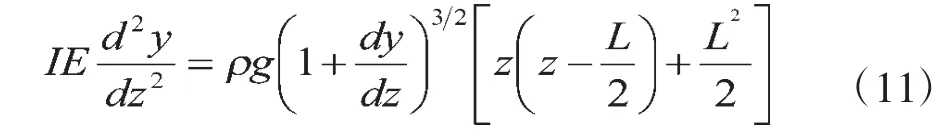
其中：I是梁的横截面关于其主轴的惯性力矩；E是弹性模量；常数ρ是梁的线密度；g是重力加速度。

选取参数L=2m，线密度ρ=10kg/m，惯性力矩与弹性模量的乘积 IE=2400kg·m3/s2[11]。

根据以上条件，确定出悬臂梁中扰度最大的位置以及求出相对应的最大扰度，作出悬臂梁扰度图（z-y图）。

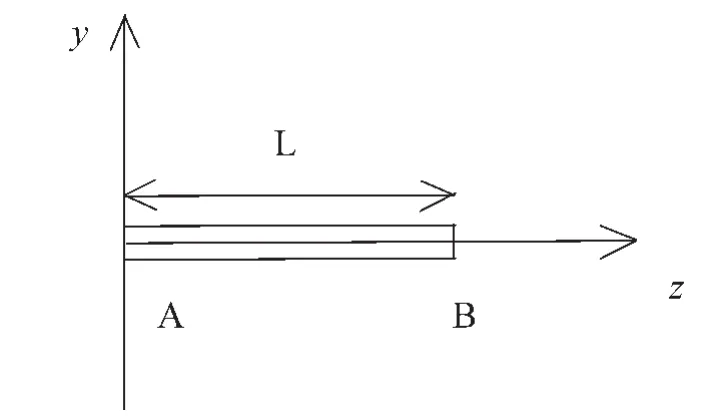
图1 悬臂梁示意图

4 MATLAB近似求解

将区间[0,2]进行100等分，采用经典四阶RK公式计算。

用RK求解微分方程的MATLAB程序[12]如下：function RK4=RK4(a,b,m)

运行MATLAB程序得出悬臂梁扰度图（z-y图）如图2所示。

图2 悬臂梁绕度图

再运行程序得出近似解：最大扰度在端点B出现，即ymax1（2）=16.48cm。

5 解析法精确求解

将已知参数L=2m，线密度ρ=10kg/m，惯性力矩与弹性模量的乘积 IE=2400kg·m3/s2代入（11）式，化简求解得：

对（15）式求最值得出：当z=2时，即在悬臂梁最右端，挠度最大，ymax2（2）=16.67cm。

6 结论