舵空化的精细流场及其非定常水动力性能数值计算

于安斌，叶金铭，王友乾

1海军工程大学舰船与海洋学院，湖北武汉430033

2海军驻上海地区装备修理监修室，上海200135

0 引 言

随着现代船舶朝着大型化、高速化的方向发展，处于螺旋桨尾流中的舵的空化剥蚀现象越来越严重，桨和舵干扰下的舵的水动力特性与空泡性能受到越来越多的关注。舵空化除了会对本身造成严重的剥蚀外，还会引发严重的结构振动和辐射噪声，对船舶舒适性及舰船隐身性提出了严峻的挑战［1］。叶金铭等［2-4］针对水面高速舰船舵的空化问题，设计了一种抗空化的扭曲舵。为了研究普通舵和扭曲舵的空化特性，建立了桨后舵片空泡的面元法数值计算方法，并对这2种舵的空化起始航速进行了比较。韦喜忠等［5］在大型空泡水筒中进行了导管桨后舵的水动力性能测试和空泡观测研究，主要考察了不同舵角下舵的定常水动力性能。何苗［6］基于面元法对桨和舵系统的非定常水动力性能进行了预报，主要研究了螺旋桨性能的变化。

当前，关于舵空泡的研究主要集中在形状和范围上［7-11］。空化发生后，舵的水动力性能必然会受到影响，但目前有关这方面的研究相对较少，尤其是针对空化状态下舵的非定常水动力性能方面的研究更是鲜有涉及。鉴于此，本文将采用CFD方法对某船桨和舵模型的空化与非空化2种状态进行计算，探讨舵空泡的周期性变化，并就空化对舵非定常水动力性能影响的规律进行总结与分析，用以为评估空化发生后舵的水动力性能及进行舵的优化设计提供技术支撑。

1 舵空泡计算

1.1 计算对象及工况

建立某型船的桨和舵模型，该船为双桨双舵，螺旋桨为内旋桨。按照一定的缩尺比，得到桨和舵的几何参数如下：舵剖面为某NACA翼型，舵展长L=198.7 mm，螺旋桨直径D=240 mm，毂径比为0.28，桨叶数为5。其中，舵轴与螺旋桨桨盘面中心的纵向距离为210.5 mm，横向距离为29.5 mm。

针对实船螺旋桨转速为278 r/min，航速为Vs的工况，采用STAR-CCM+软件对缩尺比下的舵空泡进行计算，舵角分别为0°，3°和5°。进行空化计算时，需要满足进速系数相等和空泡数相等，其中，实船空泡数公式为

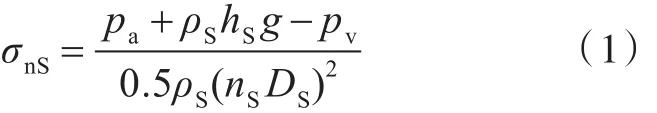
式中：pa为大气压力；ρS=1 026 m/kg3，为海水密度；hS为实船舵浸深；pv为饱和蒸汽压力；nS为实桨转速；DS为实桨直径。

模型空泡数为

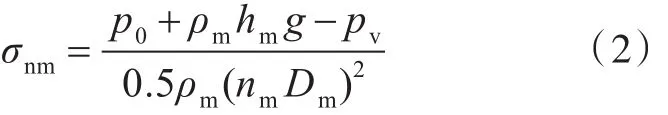
式中：p0为环境压力；ρm=1 000 m/kg3，为淡水密度；hm为模型舵最易发生空化位置的浸深；nm为模型桨转速；Dm为模型桨直径。

换算后，得到的桨和舵的空化参数如表1所示。

表1 桨和舵模型空化计算参数Table 1 Model parameters of propeller and rudder for cavitation calculation

1.2 计算域及网格划分

整个计算域为圆柱形，分为螺旋桨附近的旋转域、舵域和外域3个子域，均采用结构化网格进行划分，网格总数为1 344万。计算域的边界条件、大小及相对位置如图1所示。

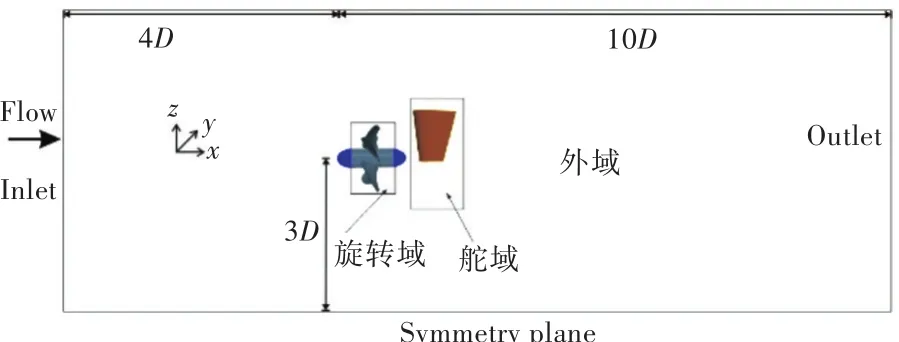
图1 计算域Fig.1 Computational domain

为了提高舵表面空泡计算的精度，对舵表面网格进行加密，轴向节点数设为150，垂向节点数设为100，并对舵前方来流处的计算域进行加密以精确捕捉桨后尾流（图2）。同时，考虑到舵边界层内的流动对舵空泡计算影响较大，将舵表面网格的第1层厚度设为0.1 mm，y+约为30。

图2 舵纵剖面网格Fig.2 Rudder longitudinal section grid

1.3 空化模型

采用 Sauer和 Schnerr［12］提出的空化模型，其定义的源项Re和Rc如下所示。

当pv＞p时，

当pv＜p时，

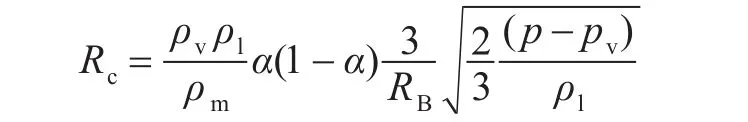
式中：p为水汽周围液体的局部压力；ρv为水汽密度；ρl为液体密度；α为蒸汽项体积分数。

其中，气泡半径RB的定义如下式：

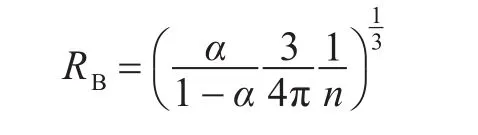
式中，n为气泡数密度，并假定为常数，默认值为1013。

1.4 求解方法

由于VOF方法主要用于模拟空泡流场中气、液两相流的相互作用，故采用SSTk-ω湍流模型和VOF方法求解空化和非空化这2种状态。对于空化工况，环境压力设为32 740 Pa，当气体体积分数αv＞0.1时，即认为空化发生；对于非空化工况，环境压力设为大气压。在计算过程中，各方程的求解均采用二阶迎风格式，2种工况下的出口压力设置参数保持一致，时间步长为每时间步旋转 1°。

1.5 舵空泡试验及计算结果

1.5.1 实船舵空泡观测试验

为了加深对实船舵空化的了解，采用试验方法观察某型实船舵在一定航速和一定舵角下的空化情况。试验通过伸到船体外部的内窥镜来实现对舵空化的观测。试验时，将内窥镜通过事先开设的观察孔伸到船体外侧，以内窥镜作为相机镜头，连接到电脑以实时成像，其示意图如图3所示。在试验过程中，首先通过转动内窥镜由电脑实时显示的图像来寻找一个周向最佳观测位置，以合理记录空泡产生和发展的区域；然后在达到所需工况时，通过电脑进行数据采集和存储。

1.5.2 数值计算方法验证

试验数据为从舵的右前方船底板向下观察所得结果，视野覆盖舵面下端至中上部区域。考虑到舵前进流主要受螺旋桨的影响，故船体对舵前来流的影响可以忽略不计，同时忽略舵空泡尺度效应的影响，然后将桨后舵的数值计算结果与实船观测结果进行对比以验证数值方法的可靠性，如图4所示。图4（a）为0°舵角下的舵空化计算结果与实船观测结果对比；图4（b）为3°舵角下的舵空化计算结果与实船观测结果对比。其中，CFD计算结果为αv=0.1的等值面。由图可以看出，数值计算得到的空泡形状与试验观测结果吻合较好，同时空泡在展向和弦向的位置也与试验结果较为一致，有力地证明了本文数值方法的可靠性。

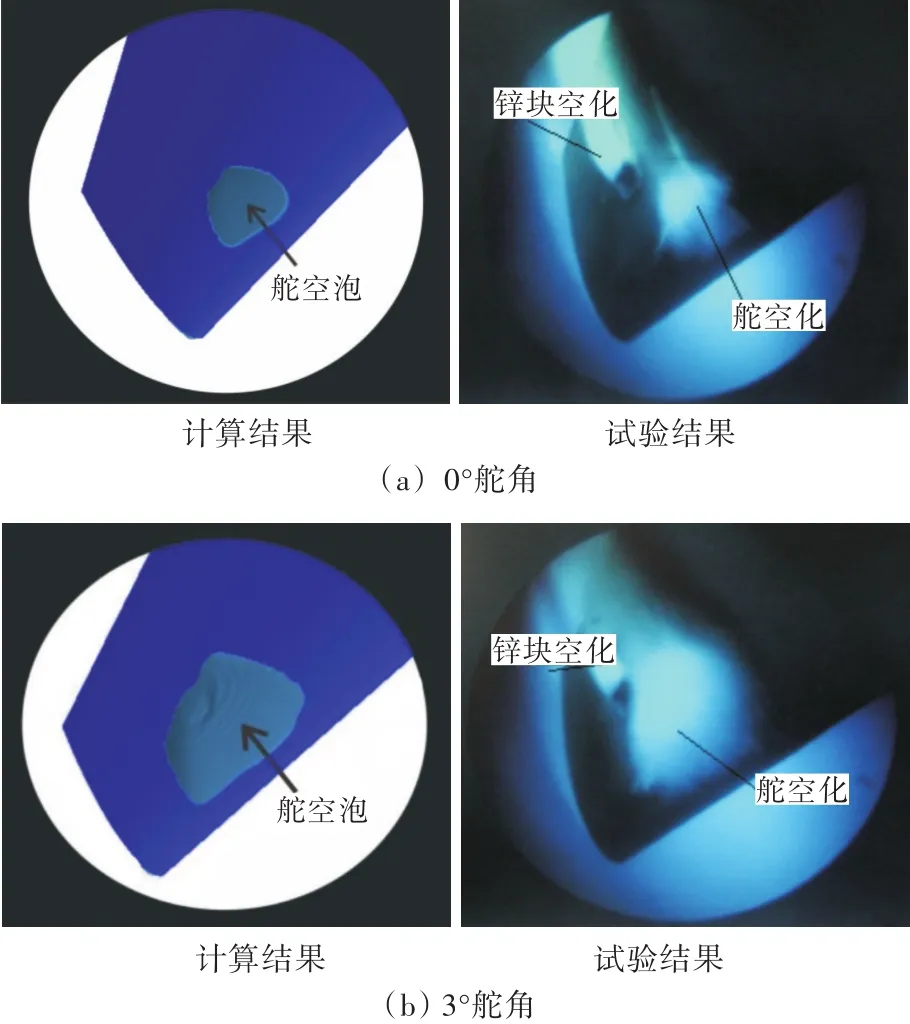
图4 舵空泡的对比结果Fig.4 Comparison results of rudder cavitation

2 计算结果与讨论

2.1 舵空化分析

因舵工作在螺旋桨后方，所以舵空泡的变化必然会受到螺旋桨尾流周期性变化的影响。以3°舵角工况下的舵空泡计算结果为例，在螺旋桨旋转一周的时间T内，舵空化的空泡体积分数（空泡体积与舵计算域的比值）变化曲线如图5所示。由图可以看出，舵空泡体积脉动的周期为T/5，其频率与叶频一致。

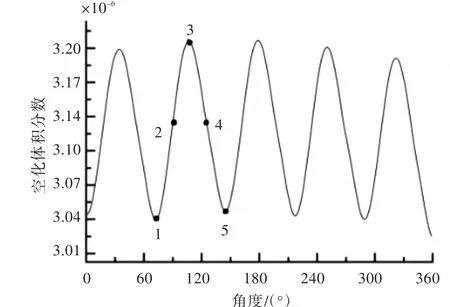
图5 舵空泡体积分数变化曲线Fig.5 Curve of the volume fraction of the rudder cavities

图6所示为一个舵空泡周期下的空泡变化情况，均匀分为了5个阶段，正好与图5中的点1～5对应。由图6（a）可以看出，在空泡发展过程中，发生了流体分离现象，且空化面积越大，流体分离越剧烈。该现象为回射流现象，是空泡发生脱落的重要原因之一。为深入分析，选取舵剖面产生回射流处的一个点作为监测点，螺旋桨旋转一周时其轴向速度变化曲线如图7所示。结合图5和图7可以看出，阶段2和阶段4为空泡体积变化率最大的时刻，此时轴向速度恰好达到速度峰值，这说明回射流现象对空泡的脱落影响较大。由图6（b）可以看出，在空泡发展过程中，空泡逐渐发生脱落，这与图6（a）中反映出的现象一致。图 6（c）为αv=0.1时的空泡厚度示意图，从图中可以清楚地看到空泡体积变化的过程。

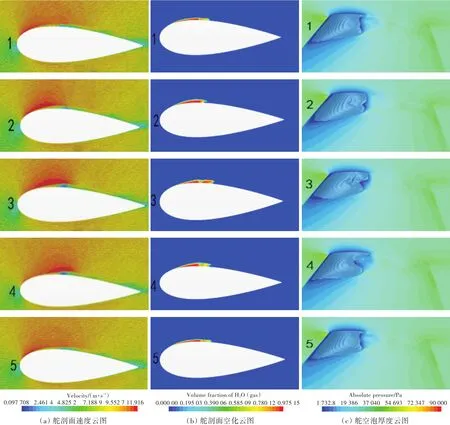
图6 单周期内的舵空泡变化情况Fig.6 Variation of the rudder cavitation in single period

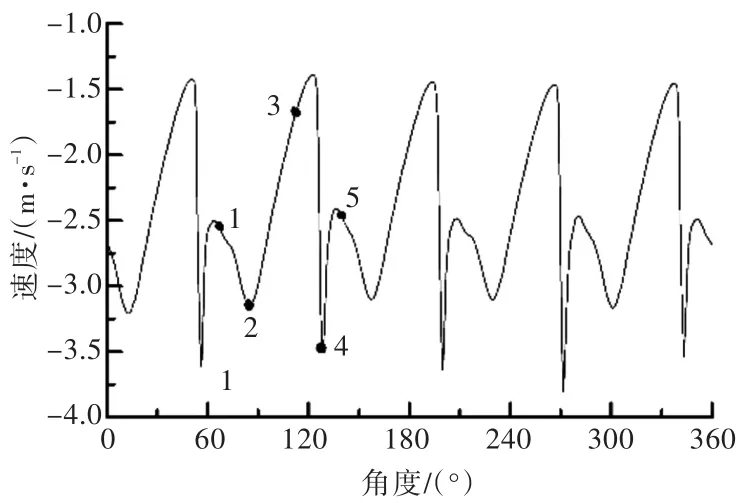
图7 轴向速度变化曲线Fig.7 Variation of axial velocity

2.2 舵水动力性能分析

2.2.1 舵横向力

图8所示为为在0°，3°和 5°舵角工况下，空化和非空化状态的舵横向力计算结果。从中可以看出，舵横向力振动频率与叶频一致。在0°舵角工况下，非空化状态的舵横向力时均值为77.0 N，空化状态的时均值为78.0 N；在3°舵角工况下，非空化状态的舵横向力时均值为157.9 N，空化状态的时均值为160.4 N。这说明空化现象未降低舵的横向力性能，此时舵的空化面积相对较小，对横向力性能无影响。在5°舵角工况下，空化状态下的舵横向力时均值为199.2 N，非空化状态下的舵横向力时均值为211.9 N。此时，舵空泡范围变大，空化现象降低了舵的横向力性能。

为进一步分析，分别截取0°，3°和5°舵角工况下舵吸力面空泡发生位置处3个展长位置（0.3L，0.4L和0.5L，舵下端面为0L，舵上端面为L，L为舵展长）的剖面压力系数曲线，如图9所示（弦向0为舵前缘，1为舵后缘）。由图可以看出，在0°和3°舵角工况下，空化状态和非空化状态所围面积基本一致，故舵横向力大小基本一致；而在5°舵角工况下，非空化状态的低压继续降低，空化状态下的低压保持不变，从而使空化状态下的舵横向力性能降低。

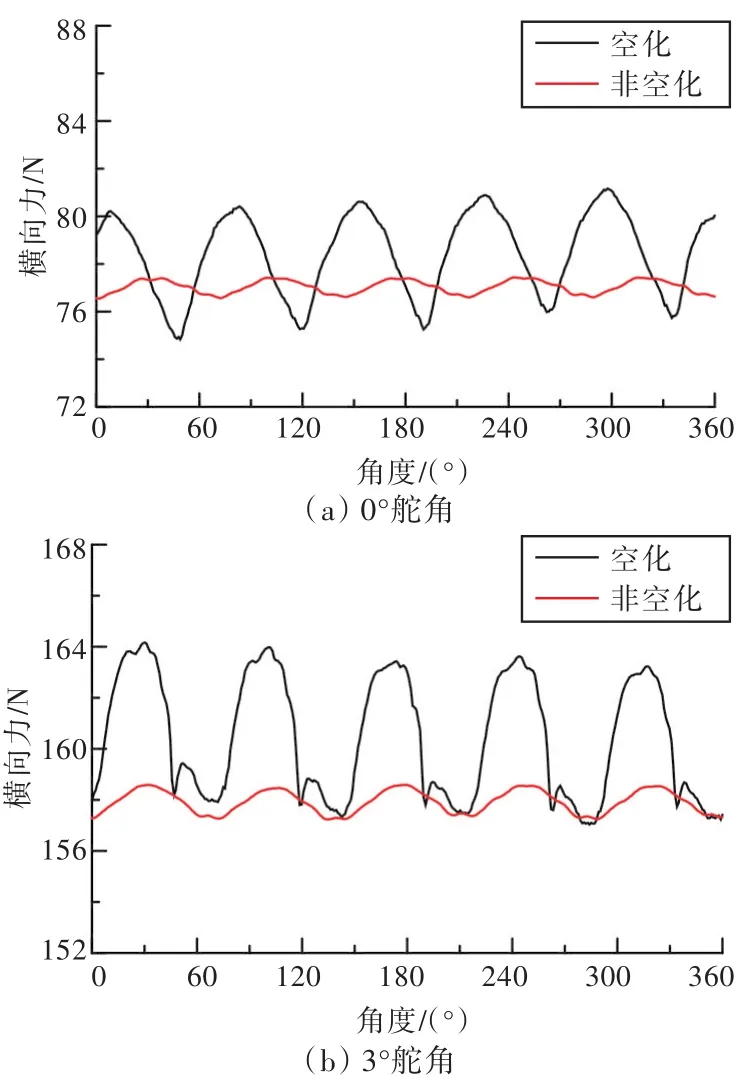
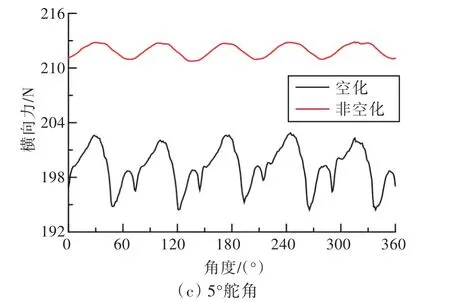
图8 舵横向力计算结果Fig.8 Computing results of lateral force for rudder

同时可知，空化现象增大了舵横向力的振动。这主要是由于舵空化体积的变化引起了其他非空化区域压力脉动的剧增，从而增加了舵横向力的脉动。图10所示为3°舵角工况下，在舵吸力面取的4个压力监测点。图11所示为对应的空化和非空化状态下的压力对比结果。由图11可以看出，在非空化状态下，受螺旋桨不均匀尾流影响而产生的压力脉动幅值较小。但一旦发生空化，压力的脉动幅值将急剧上升，约为非空化状态幅值的20倍，从而使舵的横向力振动大幅增加。同时还可以发现，压力监测点距离空化发生区域越近，压力脉动幅值就越大。由于水面舰船距离舵上端面较近，故船体的脉动力将大幅增加，从而引发较为严重的船体局部振动现象。

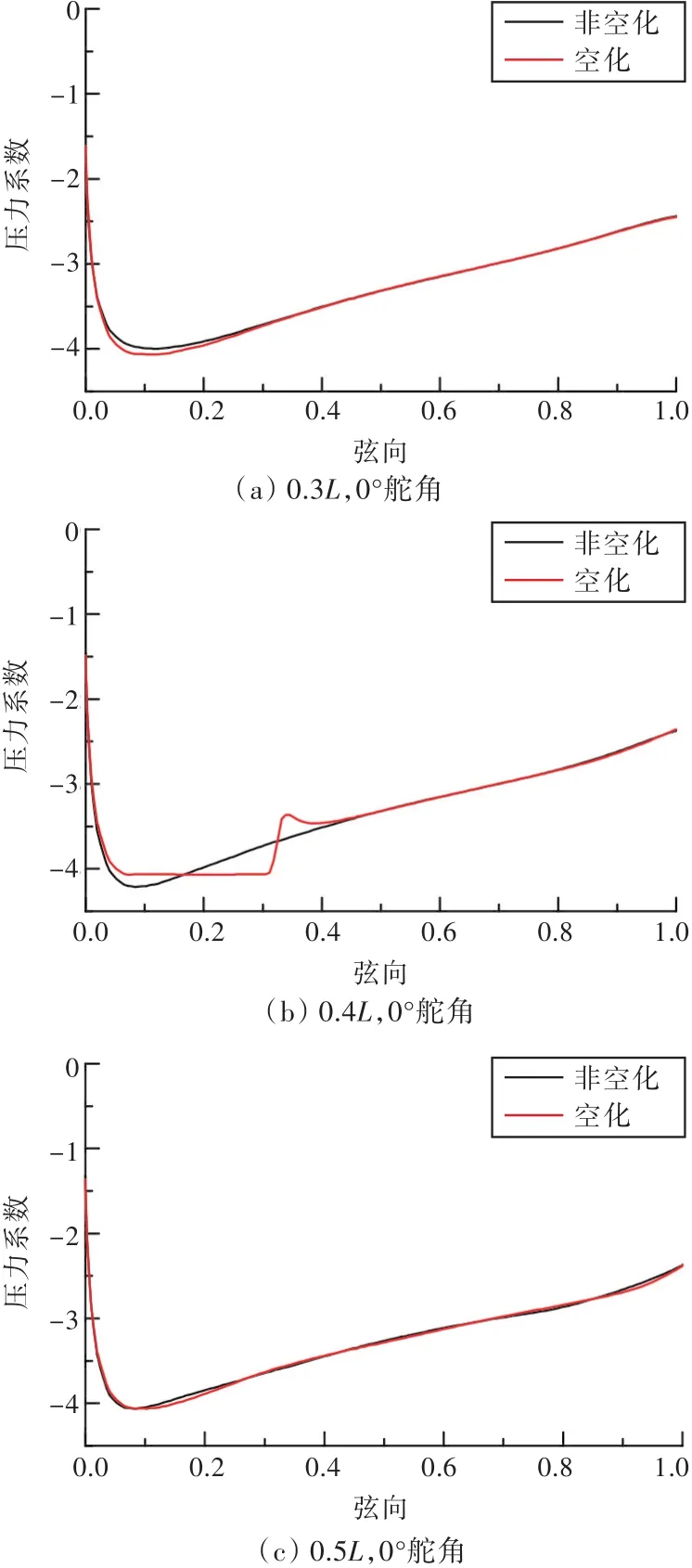
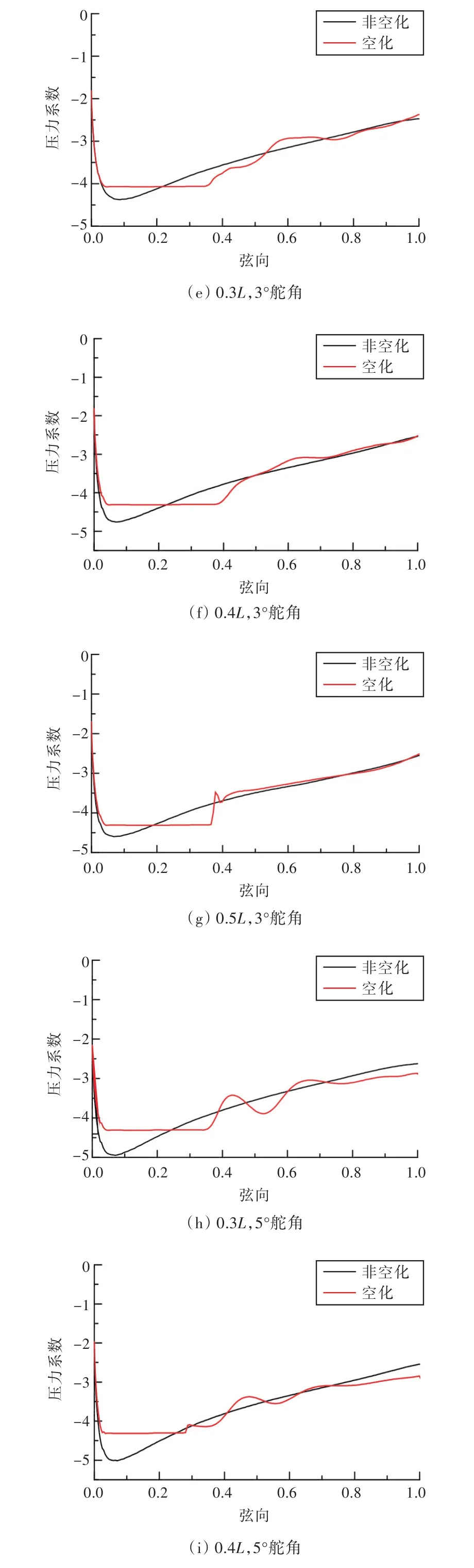
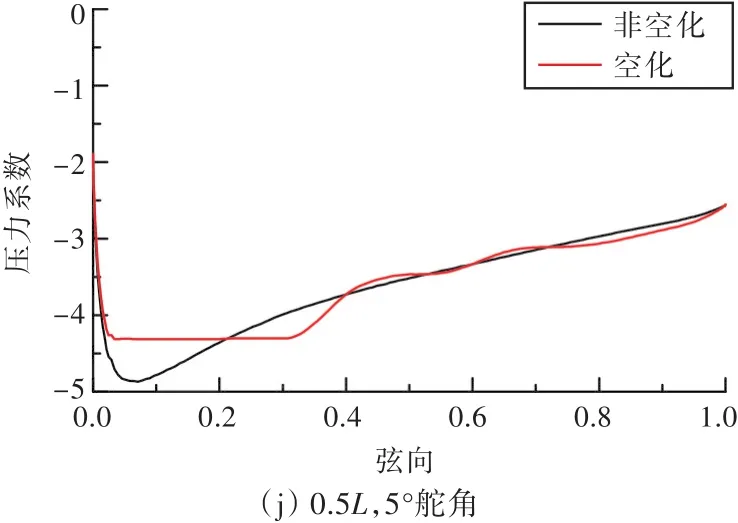
图9 舵剖面压力系数曲线图Fig.9 The pressure coefficient curves of profile for rudder

2.2.2 舵轴扭矩

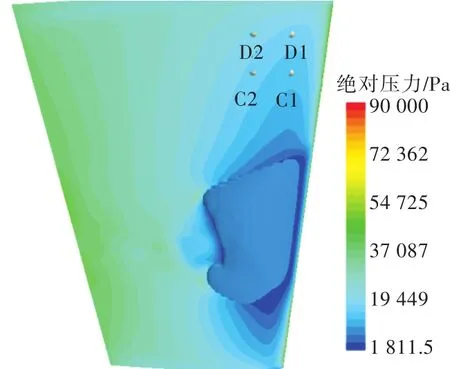
图10 压力监测点分布图Fig.10 Distribution of the pressure monitoring points

图12所示为0°，3°和 5°舵角下空化与非空化状态的舵轴扭矩计算结果。从中可以看出，舵轴扭矩振动频率与叶频一致。在0°舵角工况下，非空化状态下的舵轴扭矩时均值为1.978 N·m，空化状态下的舵轴扭矩时均值为1.986 N·m，这说明空化面积较小时空化现象对舵轴扭矩的影响也较小。而在3°舵角工况下，非空化状态下的舵轴扭矩时均值为3.402 N·m，空化状态下的舵轴扭矩时均值为3.154 N·m。在5°舵角工况下，非空化状态下的舵轴扭矩时均值为4.396 N·m，空化状态下的舵轴扭矩时均值为3.572 N·m。证明在空化面积较大时，空化现象使舵轴扭矩明显降低。

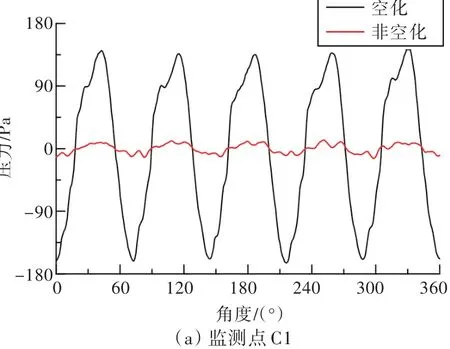
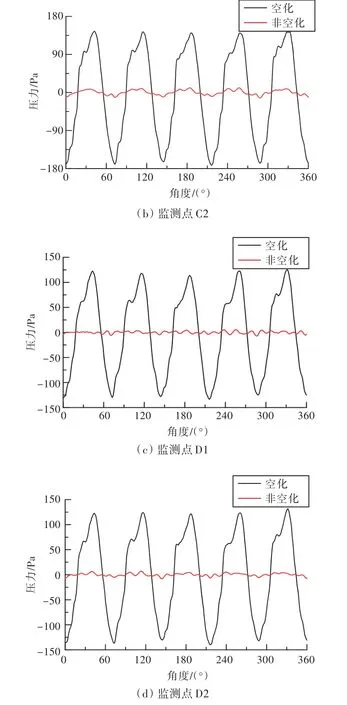
图11 各监测点压力曲线Fig.11 Pressure curves of different pressure monitoring points

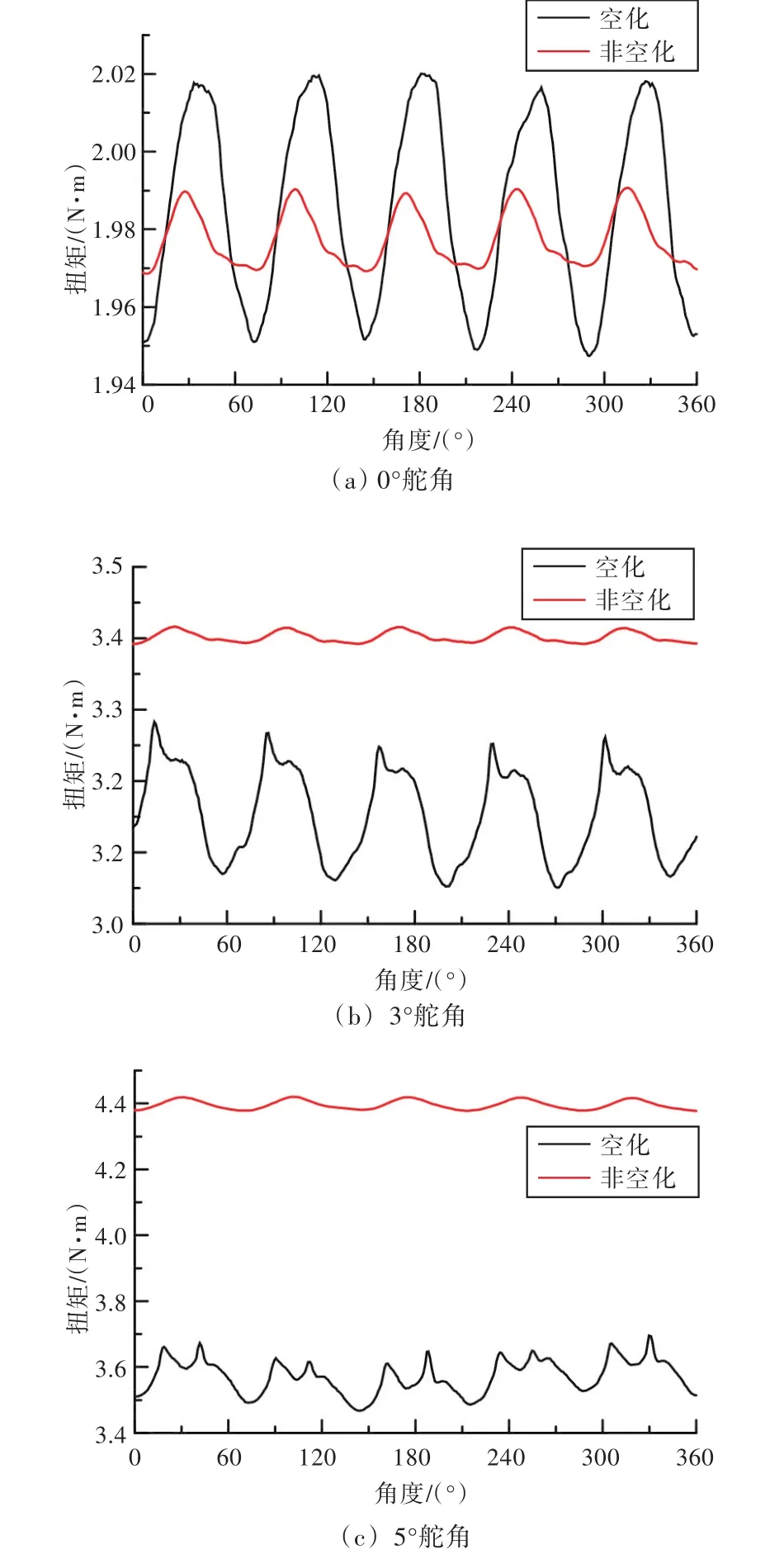
图12 舵轴扭矩计算结果Fig.12 The computing results of rudder shaft torque

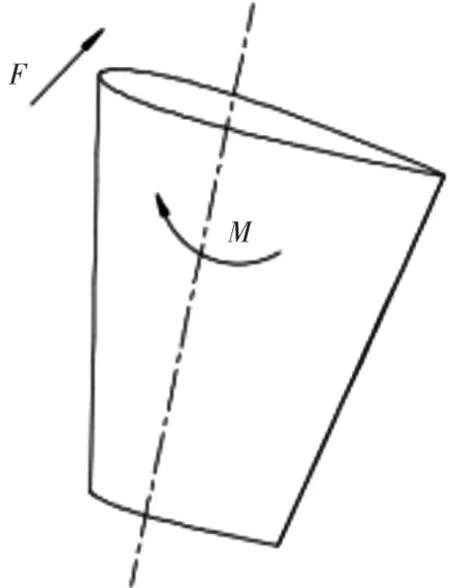
图13 舵力方向示意图Fig.13 Direction of force for rudder

为深入分析，建立了如图13所示的舵力方向示意图。图中，F为舵横向力，M为舵轴扭矩，图中所示方向均为其实际方向，舵轴所处位置为距前缘0.32b（b为各剖面弦长）处。已知空化发生位置靠近舵前缘，随着空泡面积的增大，舵轴前缘部分的受力明显减小，从而使得舵轴扭矩降低。

另外，由图还可以明显看出，空化现象的产生使得舵轴扭矩的脉动幅值明显增加，其原因与横向力相似。这将加剧舵轴控制机构的振动，增加舵轴的控制难度。

2.2.3 舵阻力

图14所示为0°，3°和 5°舵角工况下空化与非空化状态的舵阻力计算结果。从中可以看出，舵阻力振动频率与叶频一致。结合图8可以看出，与舵横向力相比，舵阻力值要小得多，这主要是因为舵表面压力与舵面垂直，在轴向的投影面积要比在横向的小得多。

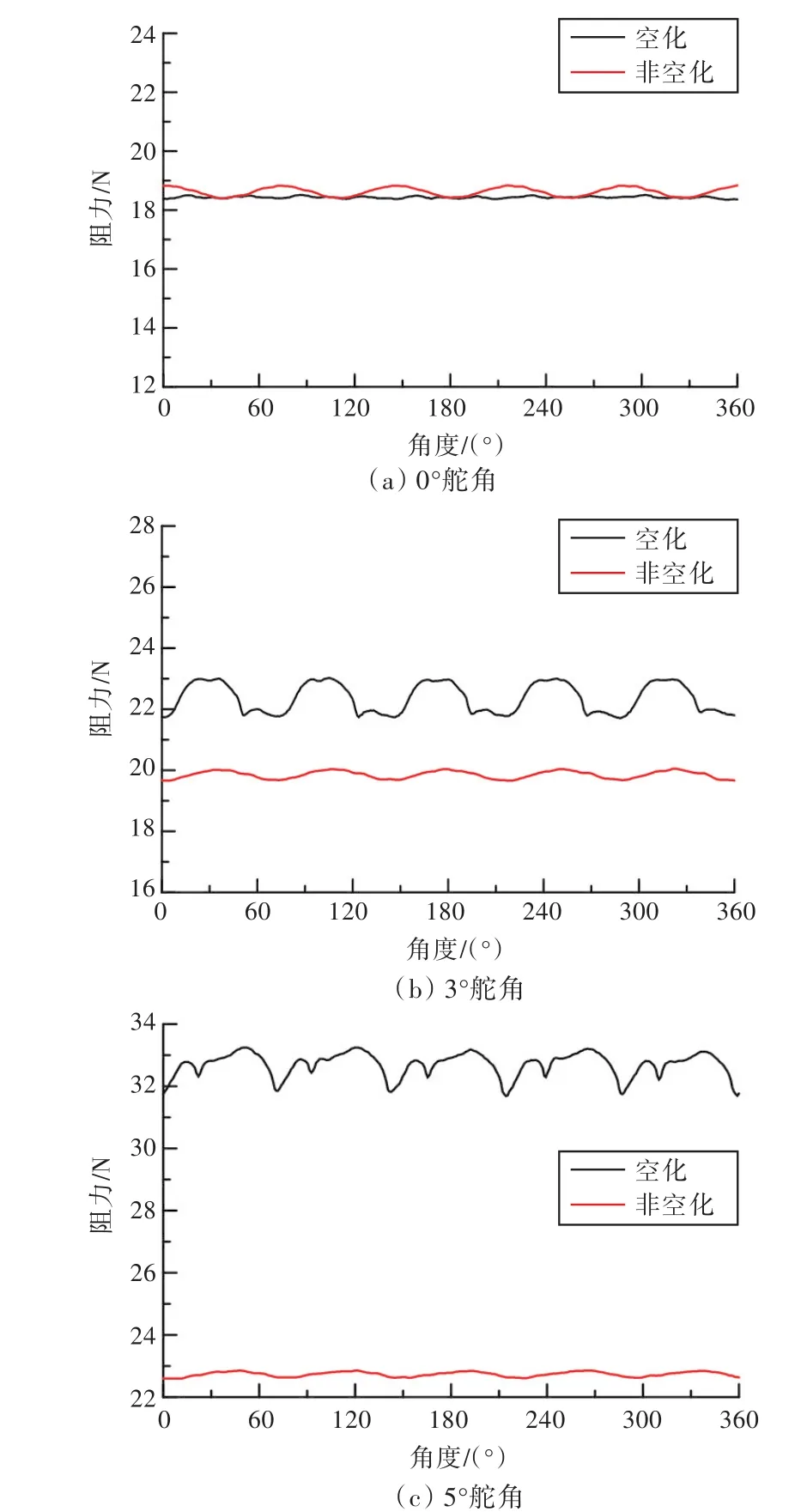
图14 舵阻力计算结果Fig.14 The computing results of rudder resistance

在0°舵角工况下，由于空化面积较小，空化状态下的舵阻力时均值与非空化状态下的舵阻力时均值近似相等。此时，空化对舵阻力的时均值影响较小。在3°和5°舵角工况下，随着空化面积和体积的增大，使得舵叶变厚，空化状态下的舵阻力时均值开始逐渐超过非空化状态下的舵阻力时均值。

同时还可以看出，随着空化面积的增大，空化状态下的舵阻力振幅迅速增加，进一步加剧了舵体结构的振动。

3 结 论

本文采用结构化网格、SSTk-ω湍流模型和VOF方法对某船桨、舵模型的空化与非空化这2种状态进行了计算，通过分析，得出以下结论：

1）针对舵空化问题进行了实船空泡观测试验，将计算得到的舵空泡范围和位置与实船试验的舵空泡进行了对比，结果较为吻合，验证了数值计算方法的可靠性。

2）对舵空泡的周期性变化进行了计算，通过对比不同时刻的舵剖面速度云图和舵剖面空化云图，发现了回射流现象，这是产生空泡脱落的重要原因之一。其中，回射流中的速度峰值对空泡的脱落产生了较大影响。

3）舵横向力、舵轴扭矩和舵阻力等非定常力的脉动频率与叶频一致，其原因在于舵的力学特性受螺旋桨尾流周期性变化的影响。

4）通过对0°和3°舵角工况的计算发现：当空化范围较小时，空化对舵力时均值的影响较小，随着空化范围的增加，空化对舵力时均值的影响明显变大，尤其是舵效显著降低，这对于在高航速大舵角工况下的水面舰船来说是非常不利的；一旦发生空化，舵非定常力的脉动幅值将大幅增加，且空化范围越大，舵非定常力的脉动幅值越大。可见，空化不仅会降低舵效，还会增大舵非定常力的脉动幅值，加剧舵叶结构振动及结构振动引起的辐射噪声。因此，建议采用抗空化扭曲舵来抑制舵空化的发生，从而降低舵空化引起的一系列不利影响。