搁置脚载荷作用下的甲板压力分布特征实验和数值分析

熊群飞，徐志亭，王福花，王德禹

1上海交通大学船舶海洋与建筑工程学院，上海200240

2中国船舶及海洋工程设计研究院，上海200011

0 引 言

舰船甲板上通常会装载物资、轮式车辆和其他类型装备，这些载荷在计算甲板强度时通常被当作轮印载荷来处理，确定其大小对在此情况下的甲板结构设计有着非常重要的意义。

国内学者对轮印载荷作用下的甲板结构有较多的研究。张文强和刘俊［1］研究了多轮印载荷作用下车辆甲板板厚的设计方法；彭兴宁和徐向东［2］利用有限元程序对甲板的非线性响应进行计算，给出了轮印载荷作用下甲板结构的设计图谱；刘聪等［3］研究了轮印载荷在加筋板上的分布以及加筋板面板的初始缺陷、加强筋高度以及加筋板面板厚度对轮印载荷分布的影响，并进行了实验验证。此外，对于车辆甲板、飞行甲板等的设计在劳氏军用规范、中国船级社规范等［4-8］中也都有规定。由上述研究成果和规范来看，它们一般将车辆作用在甲板上的轮印载荷视作接触面积内的均布压力来处理。本文所分析的某大型装备通常由数个铝合金材质的搁置脚搁置在舰船甲板上，其承受的重量大，与甲板之间存在着复杂的非线性接触，且两者之间的接触面积较大，其纵向尺寸与纵骨的跨距相当，横向尺寸与纵骨的间距也相当，故计算时不能将搁置脚载荷等效为均布压力来处理。

目前，针对承受此类载荷的甲板结构强度的研究较少，曾鸣和郑朝斌等［9-11］对搁置脚与甲板结构的非线性接触力进行了计算，并与采用均布载荷直接加载在甲板板上的线弹性计算结果进行了比较，结果表明，两者差别很大。而船级社的相关规范对这种甲板并不适用，故有必要对搁置脚与甲板进行非线性接触分析，并对有限元分析结果进行实验验证，以找到搁置脚载荷的作用特征。

本文将采用非线性接触方法分析搁置脚作用在板格上时甲板的压力分布特征，以找到甲板板应力最大时搁置脚的作用位置。同时，根据有限元分析结果，设计一个缩尺模型实验装置。然后，采用薄膜式压力传感器测量搁置脚在甲板上不同位置时的压力分布，并与有限元计算结果进行比较分析，以得到搁置脚载荷在甲板板和强横梁上的分配关系。在此基础上，提出一种运用等效轮印载荷代替搁置脚载荷的简化计算方法。

1 非线性数值分析

1.1 接触问题概述

接触问题在工程技术中十分常见，与一般的力学问题相比，其难点主要是接触力学表面的不确定性，两个接触体间的接触面积和压力分布随着外载荷的变化而变化，部分边界条件也随着加载过程发生不可逆的改变，故接触问题实质上是由边界条件的可变性和不可逆性产生的边界非线性问题，若再考虑材料和几何的非线性，将更加复杂。现代工程中的接触问题一般采用数值方法来求解。

本文采用ABAQUS软件计算接触力，通过ABAQUS/Standard使用Newton-Raphson法来求解非线性问题。具体求解过程如下：首先，假设接触状态和可能的接触区域；然后，按这些状态所对应的边界条件，根据两个接触体间的面积和压力分布随着外载荷变化的特点来建立方程并求解；最后，计算结果应满足假定接触状态对应的判定条件，否则，需要修改接触状态继续求解，直至满足相应的判定条件为止。上述计算是一个迭代求解的过程。

1.2 计算模型

用于接触计算的有限元模型包括搁置脚模型和甲板模型。搁置脚模型为楔形前端的铝合金箱形结构，内部由横向和纵向隔板来支撑，单元类型为S4R壳单元，网格尺寸为8 mm，材料的弹性模量E=72 GPa，泊松比μ=0.33，如图1所示。甲板模型由甲板板、强横梁、纵桁、纵骨、支柱等组成，均采用S4R壳单元模拟，整体网格尺寸为50 mm，并在与搁置脚接触区加密为10 mm，甲板材料为钢材，弹性模量E=210 GPa，泊松比μ=0.3。

图1 隐去顶板的搁置脚模型Fig.1 The undercarriage model with hidden roof

研究中，将上述2个模型装配在一起，并在搁置脚底部和甲板板之间建立接触对。接触对由1个主面和1个从面组成。由于甲板的刚度、面积和单元尺寸较大，故本文将甲板板作为主面，搁置脚底面作为从面，主、从面的网格尺寸分别为10和8 mm，两者相差较小，符合接触计算的要求。主、从面的接触属性定义如下：法向作用定义为硬接触，切向采用库伦摩擦模型（Coulomb friction model）。考虑到甲板涂层材料的影响，本文定义的钢和铝合金的摩擦系数为0.45。

甲板模型边界条件为其底部和支柱处简支。模型载荷为传递到搁置脚的重力，单个搁置脚所承受的总力F由重心位置和搁置脚位置确定。施加在搁置脚顶部的载荷合力的作用线必须通过底部中心，而搁置脚的顶部与底部面积并不相同，故不能简单地施加均布载荷。处理方法是：在底部中心对应的搁置脚顶部位置建立参考点，将顶部所有节点和参考点建立多点约束，并将F作用在该参考点上，如此顶部这些点的合力就通过了底部中心。具体装配和加载模型如图2所示。

图2 装配模型Fig.2 The assembled model

1.3 计算工况

根据实际装载情况，搁置脚纵向与纵骨方向平行，为寻找甲板板应力最大时的工况，需要调整搁置脚的纵向（纵骨方向）和横向（强横梁方向）位置。对于横向来说，显然搁置脚作用在2根纵骨之间时的甲板板应力最大；而在纵向位置需要移动搁置脚，以建立不同的分析工况。根据搁置脚相对于强横梁的位置，建立了如图3所示的5种计算工况，相邻工况移动的距离相似，即从横跨1根强横梁到同时作用在2根强横梁上，包含了搁置脚所有可能的纵向位置。图4所示为隐去甲板板后工况3的位置示意图。

图3 计算工况示意图Fig.3 The sketch of computation conditions

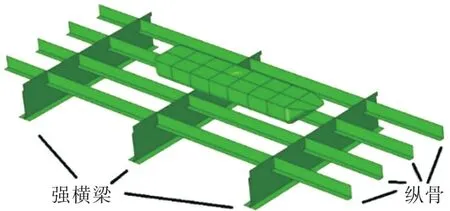
图4 工况3计算示意图Fig.4 The sketch of computation condition 3

1.4 计算结果分析

采用有限元软件进行的接触计算结果表明，在工况3下，甲板板应力最大，达到459 MPa，此时的应力分布和接触力分布如图5和图6所示。从图5可以看出，在工况3下，甲板板的最大应力出现在搁置脚前端2块小的接触区域，每块区域面积约为20 mm×20 mm，这2块区域是甲板板最危险的位置，其他部分的应力水平则较低。而从图6可以看出，甲板板的接触力主要分布在强横梁处和搁置脚前端，搁置脚前端2块应力最大的接触区域也是接触压力集中的部位。此外，强横梁处同样具有较大的接触力，但是这部分接触力主要由强横梁承受，故强横梁处甲板板的应力值并不高。

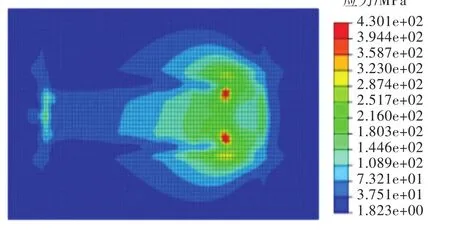
图5 工况3甲板板应力云图Fig.5 The stress contours of deck plate in condition 3

图6 工况3甲板板接触压力分布Fig.6 The contact pressure distribution in condition 3

为研究接触力沿纵向分布的规律，在每个纵向位置，将甲板板横向各节点的接触力求和，记为f，并除以作用在搁置脚上的总力F，可得到接触力沿纵向分布的比例曲线，如图7所示。从图可以看出，接触力集中在强横梁处和搁置脚前端，其他位置的接触力较小。进一步对曲线中2个接触力集中处附近的节点力求和，即对峰值点及其相邻2个点的接触力求和，从而可得到作用在搁置脚前端的接触力占总载荷的23%，强横梁处的占比为61%，两者的接触力达到了总载荷的84%。将搁置脚前端接触合力记为F1，图8所示为各工况下搁置脚前端接触力的占比，即F1/F。由图可以看出，从工况1～工况5，随着搁置脚的移动，前端接触力是先增后减，并在工况3时达到最大值。由此可以得出结论：在最危险工况下，集中在搁置脚前端两侧的接触力使甲板板应力达到最大值，且接触力占总接触力的23%，前端两侧的接触区面积各约为20 mm×20 mm。

图7 工况3接触力分布Fig.7 The distribution of contact force in condition 3

2 甲板压力分布实验

2.1 实验模型

基于上节有限元计算结果开展了甲板压力分布实验，以对数值计算结果进行验证和修订。实验模型为钢制甲板模型和铝合金材质的搁置脚模型，各构件类型和尺寸与有限元模型一致，如图9所示。为方便传感器布置，甲板模型由支柱支撑，如图9（a）所示，每个边界平均设置4个支柱，4个边界共12根，再加上模型内部固有的6根支柱，一共18根支柱。

由于甲板尺寸和载荷都较大，所以通过吊运3个方形加载块的方式完成加载，如图10所示。同时，由于方形加载块质量均匀，加载时只需将加载块的中心线与搁置脚底部的中心线对齐，即可保证载荷的作用线通过搁置脚底部中心，这基本上与实际情况和有限元计算的加载方式相符。

图9 实验模型Fig.9 The experimental model

图10 加载示意图Fig.10 The sketch of loading

2.2 工况与传感器布置

实验测量的物理量包括甲板板应力和搁置脚与甲板间的接触压力，其中甲板应力由三向应变片测量，接触压力采用薄膜压力传感器测量。实验共设置5个工况，与上节有限元计算的5个工况相对应，包含搁置脚典型的装载位置。每个工况进行3次实验，取3次结果的均值。

每个工况的压力测点有16个，根据有限元计算分析得到的接触力分布规律，将测点集中布置在搁置脚前端和强横梁处，各工况的压力测点位置如图11所示。设置应力测点的主要目的是为了测量甲板的最大应力，而根据有限元分析结果，工况3的甲板应力最大，因此根据工况3的有限元计算结果确定应力测点，并只在工况3时进行测量，1号测点位于板格中心，2号测点布置在有限元分析结果的应力最大点的对应位置，如图12所示。图中，搁置脚为工况3所在的位置。

图11 压力传感器布置Fig.11 The arrangement of the pressure sensors

图12 应变片布置Fig.12 The arrangement of the strain gages

2.3 实验结果分析

本次实验测得各工况的压力结果如表1所示。从表中可以看出，实验测得的压力结果与有限元方法计算的结果总体上能够对应，但实验结果显示，搁置脚与甲板接触压力实际上并未如有限元结果那样集中，很多采用有限元方法计算的压力为0的点却有压力值。这主要是因为实验模型不可能像有限元模型一样理想平整，实际上搁置脚和舰船甲板会不可避免地有各种变形，实验的接触力分布特征比有限元计算的更接近实际情况。而且由于实验的接触面积很大，载荷也很大，因此这些小于10 MPa的接触压力结果可以接受，压力相对较大的测点更能反映甲板板的压力分布特征。

为了直观地看出实验的压力分布，本文提供了各工况下的压力三维分布图，如图13所示。从图中可以看出接触力分布的大致规律如下：在工况1～工况4下，搁置脚前端作用在甲板板上的接触力是先增后减，并在工况3时达到最大值；在工况5下，搁置脚前端已压在强横梁上，此时对甲板应力影响不大，相反，横梁承受的接触力是先减小后增大；虽然工况2与工况4的搁置脚前端的压力值偏小，但是强横梁处的压力变化也验证了这种趋势。上述结果印证了有限元的计算结果。

由于布置在搁置脚前端的传感器数量较少，不能得出前端接触压力的精确分布，故在工况3的基础上补充了2个加密工况3a和3b。工况3a将16个压力传感器全部布置在接触力集中的强横梁附近，工况3b将16个压力传感器全部布置在搁置脚前端，搁置脚位置和加载条件与工况3一致，如图14所示。

表1 接触压力的实验结果与有限元计算结果对比Table 1 Comparison of contact pressure results acquired by FEM and experiment

图13 不同工况下的实验压力三维分布图Fig.13 Three dimensional pressure distribution in different conditions

图14 补充工况的压力传感器布置Fig.14 The arrangement of pressure sensors in added conditions

本文通过Matlab软件将工况3a和工况3b的接触压力结果进行插值处理得到三维分布图，如图15所示。图中，x方向为纵骨方向，即搁置脚长度方向，y方向为强横梁方向，即搁置脚宽度方向。从图中可以看出，搁置脚前端的接触力分布在两侧的2个小块区域上，对压力曲面下的体积积分可得到分布在搁置脚前端的接触力约占总载荷的26%。

图15 三维接触压力云图Fig.15 Three dimensional plot of contact pressure in added conditions

实验的应力结果如表2所示。实验中仅测量了最危险工况，即工况3的应力结果。由表可以看出，最大应力点在搁置脚前端两侧，为394.33 MPa，有限元计算值为459 MPa。

表2 工况3的应力实验结果与有限元计算结果对比Tab.2 Comparison of stress results acquired by FEM and experiment

3 甲板板的简化计算

在对承载搁置脚的甲板板进行强度计算校核时，需要进行复杂的非线性接触计算。根据搁置脚作用在甲板上时的压力分布特征，可以将搁置脚载荷简化为类似于其他普通轮式车辆的轮印载荷，将高度的非线性接触计算转化为线弹性计算，从而简化甲板板的计算校核过程。

上述有限元计算和实验结果都表明，作用在甲板板上的搁置脚载荷主要为集中在强横梁处和搁置脚前端两侧块状区域的接触力，由于强横梁附近的接触力主要由强横梁承担，因此主要是搁置脚前端的接触力使甲板板具有较大的应力。为进行甲板板的简化计算，可以将搁置脚载荷视为2个块状区域内的均布压力，然后研究块状区域的位置、作用面积和均布载荷的大小。鉴于工况3是危险工况，其数值计算和实验中2个块状区域的作用位置与搁置脚前端两侧接触力集中的区域一致。有限元计算和实验测得的搁置脚前端的接触合力F1分别为0.23F和0.26F，两者相差不大，这里取0.25F，从而可以近似认为2个块状区域内均布压力p的大小均为

式中，a为接触区长度。

接触区域的面积，或者说参数a的值不能直接得到。虽然上文采用有限元计算方法得到了块状区域的尺寸为20 mm×20 mm，但实验结果表明，用有限元方法计算得到的接触压力分布异常集中，前端作用区域的宽度基本上只有2个网格，而且在有限元计算与实验测得的前端接触合力基本一致的情况下，实验的甲板应力却比有限元计算值小16%，这也表明采用有限元计算方法得到的接触区域面积偏小，与实际不符。为说明采用有限元方法计算的这种接触力集中的现象，分别用10，25和50 mm尺寸的网格对工况3进行了接触计算，具体结果如表3所示。

由表3可以看出，随着网格尺寸的增大，搁置脚前端的接触总力基本不变，接触区长度a逐渐增大，而且始终比网格尺寸大1倍。图16所示为在各网格尺寸下前端接触区的云图对比。由图可见，接触力总是集中分布在一个节点上，接触区域为该节点周围的4个网格，可见，利用有限元方法计算得到的接触区长度a是不可信的。从表3还可以看出，网格尺寸和接触区长度对应力有较大影响，故可以认为实验得到的应力结果为真实的最大应力。

表3 不同网格尺寸的计算结果Table 3 Calculation results of different mesh sizes

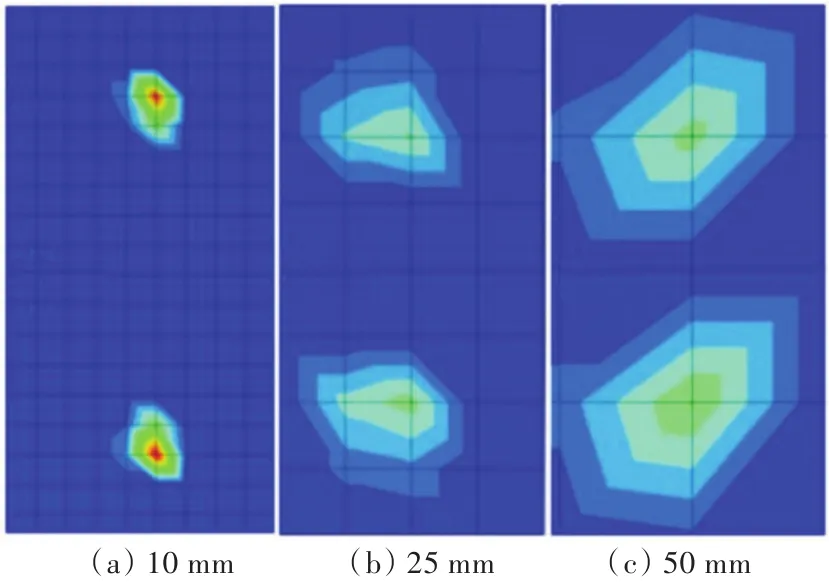
图16 不同网格尺寸的接触区域Fig.16 The contact areas of different mesh sizes

为确定参数a的取值，建立甲板板的简化计算模型，进行多组不同接触区域长度下的简化计算，得到不同接触区域长度下的甲板板应力结果，并与实验测得的应力结果进行比较，若与实验测得的应力相同，则在此计算工况下的接触区域长度即为参数a的取值。

简化计算模型采用3×3板格，板格的长度为甲板纵骨跨距，宽度为纵骨间距，厚度与接触计算模型一致。

采用板单元建模，网格尺寸为10 mm，在模型四周边界取为固支边界条件，各板格四周（即纵骨和强横梁位置）为简支，载荷为作用在中间板格上2个块状区域内的均布压力，如图17所示。压力p的大小由式（1）确定，a分别取为10，20，30，40和50 mm，计算结果如图18所示。

从图18中可以看出，随着加载面积的增大，计算应力逐渐减小。当a=30 mm时，计算应力与实验应力最为接近，而且此时的计算应力略大于实验应力，采用这种计算模型是偏于安全的。图19所示为a=30 mm时的板格应力云图，其与图3给出的接触计算的应力云图较为一致，故可以认为将每块等效轮印载荷的面积取为30 mm×30 mm是较准确的。

图17 板格简化计算示意图Fig.17 The sketch of of the panel for simplified calculation

图18 板格计算应力结果Fig.18 The calculated stress results of the panel

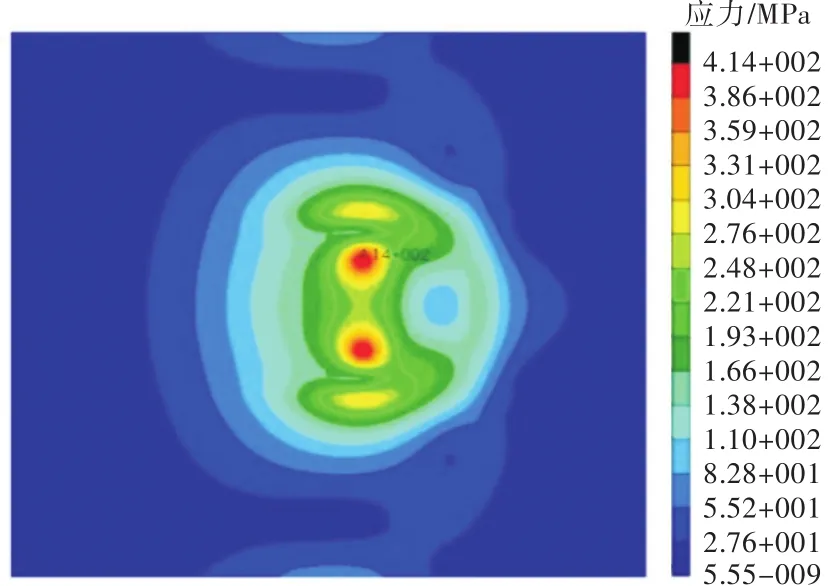
图19 a=30 mm时的板格应力云图Fig.19 The stress contours of the panel when a=30 mm

4 结 论

本文通过有限元和实验方法分析了搁置脚载荷作用下甲板的压力分布特征，并根据有限元计算和实验得到的结果对搁置脚载荷进行了简化分析，综合有限元和实验的结果，提出采用板格施加均布压力的线弹性计算方法代替复杂的非线性接触计算，将搁置脚载荷转化为等效轮印载荷，并用实验结果反推出了轮印载荷面积，得到如下结论：

1）采用实验和数值计算得到的搁置架与甲板的接触力规律基本一致，但应用有限元法计算得到的接触力分布更为集中，实验表明搁置脚前端的接触面积大于有限元计算得到的面积。

2）接触力将主要集中分布在强横梁处和搁置脚前端，其中搁置脚前端两侧块状区域内的接触力使甲板板具有较大的应力，前端的接触合力约占总载荷的25%。

3）简化计算结果与接触计算吻合较好，对此类甲板的板厚设计和强度计算具有一定的参考价值。