基于统计能量法研究肋骨对双层圆柱壳声辐射特性的影响

张恺，纪刚，周其斗，李宗威

1中国人民解放军92330部队，山东青岛266102

2海军工程大学舰船与海洋学院，湖北武汉430033

0 引 言

潜艇的主要结构形式是环肋圆柱壳，研究肋骨对环肋双层圆柱壳声辐射特性的影响，对于合理选用肋骨来降低潜艇的辐射噪声具有重要意义。

对于环肋圆柱壳的振动与声辐射问题，已经有许多学者采用解析法、有限元法/边界元法等进行了研究。Zhou等［1］和纪刚等［2-3］采用结构有限元耦合流体边界元法，研究了水下环肋圆柱壳的振动与声辐射特性。陈美霞等［4］联合有限元法和边界元法，计算了加筋圆柱壳结构在点源激励下的声辐射。王路才等［5］采用结构有限元耦合流体边界元的附加质量附加阻尼算法，研究了肋骨侧向加强对环肋圆柱壳水下振动与声辐射的影响。

这些研究大多集中在中、低频，但是振动声学问题涉及更宽的频带范围。统计能量法（SEA）是分析结构高频振动与声辐射问题的有效方法，采用统计能量法可以研究高频、宽频带范围内肋骨对双层圆柱壳声辐射特性的影响。

本文拟采用统计能量法研究环肋双层圆柱壳的宽频声辐射特性，在利用AutoSEA2软件对双层环肋圆柱壳进行建模计算的基础上，分析增加肋骨后圆柱壳SEA参数的改变；据此分析耐压壳、外壳分别增加肋骨、改变肋骨间距、改变肋骨形状对环肋双层圆柱壳声辐射特性的影响，最后分析激振力作用在不同位置时环肋圆柱壳声辐射特性的差异。

1 基本原理

统计能量法采用系统的统计描述来简化复杂的振动声学问题，其核心思想是用一个可分析的等价问题代替原有的复杂问题，从而求解具有复杂结构的高频声振问题。在SEA分析中，一个振动系统由一系列可以接收、存储、消耗、传输能量的耦合子系统构成，子系统被定义为传递波形的集合，通过假设子系统的边界条件并忽略一定的细节进行简化分析。子系统的各项参数与子系统中的传递波形特性有关，如：子系统的模态密度取决于子系统的行进波平均波速和子系统的尺寸；耦合损耗因子取决于耦合子系统的阻抗。因此，只要确定子系统内波传播的波形以及子系统在特定连接下的阻抗特性，就可以得到子系统的SEA参数。由此，将对复杂振动系统的分析转化为对每个子系统的分析。

统计能量法的思想源于热力学中能量传递关系的类比，热力学中两个物体间传递的热量正比于两者的能量差。Lyon等［6］受这种关系的启发，经过研究，发现对于2个线性耦合的单一频率振子，它们之间的能量流动也满足同样的关系：

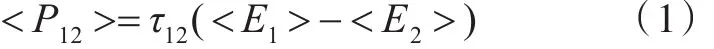
式中：＜P12＞为振子1流向振子2的时间平均功率；＜E1＞和 ＜E2＞为2个振子的能量；τ12为比例常数。

对于多结构振动之间的耦合，当满足如下假设条件时，结构之间的能量流动也有类似的关系：

1）线性保守耦合，能量在2个振形群之间的传递没有损耗，能量流动过程可逆。

2）弱耦合，2个直接连接结构之间的能量流动不受间接连接结构的影响。

3）模态均匀分布假设，子系统的振动模态在频带内是均匀分布的，间隔为Δω/N，其中Δω为带宽，N为频带内的模态数，各模态能量相等，均分各子系统的能量。

4）模态相似假设，假设子系统的模态拥有相同的模态能量、内损耗因子和耦合损耗因子。

5）同一子系统的模态之间不耦合，不同子系统间的模态相互耦合。

当满足上述假设条件时，可以将子系统的动力学参数取时间、空间、频带上的平均，采用平均量表示子系统的动力学特性。此时，子系统间的平均功率流满足：

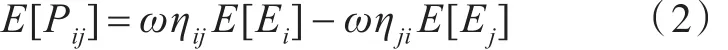
式中：E[·]为统计期望平均值符号；Pij为子系统i流向子系统j的功率；ω为中心频率；ηij和ηji为系统间的耦合损耗因子在频带上的平均值；Ei和Ej为子系统的能量。

根据能量守恒定律，子系统i的功率平衡方程为

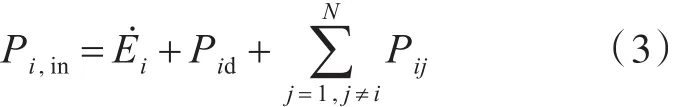
式中：Pi，in为子系统的输入功率；Ėi为子系统的能量关于时间的导数，对于稳态系统，Ėi=0；Pid为子系统的内损耗功率。

将式（3）转换成矩阵形式：

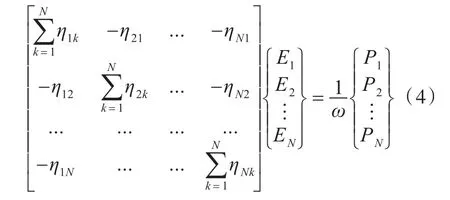
根据互易定理，对保守耦合系统，ηijni=ηjinj，其中，n为子系统的模态数。因此，可以将式（4）写成对称形式：

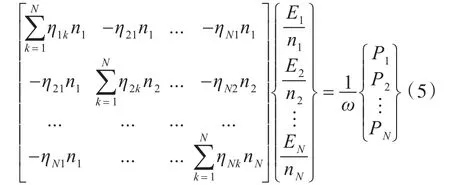
根据子系统的行进波传播特性获得内损耗因子、模态密度、耦合损耗因子等参数，根据激励获得每个子系统的输入功率，求解方程（5），得到每个子系统的能量Ei进而得到子系统的振速、声压等参数。

2 分析模型

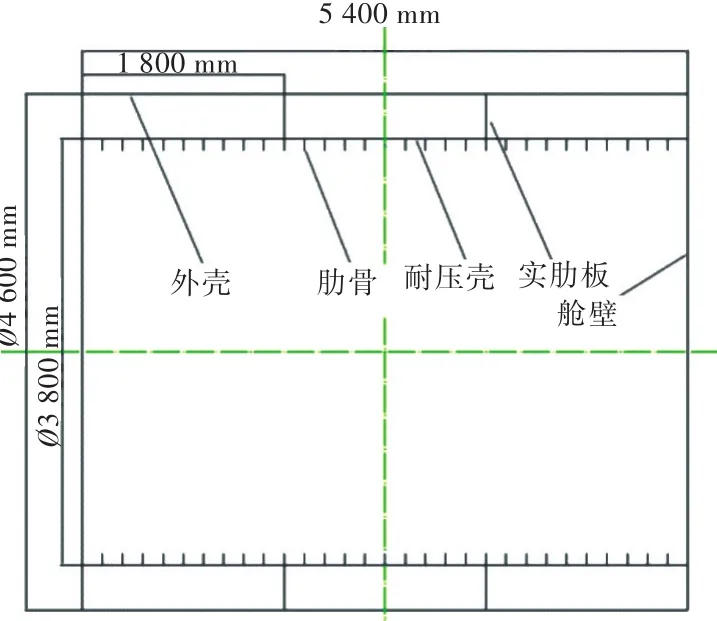
图1 双层圆柱壳模型Fig.1 Double cylindrical shell model

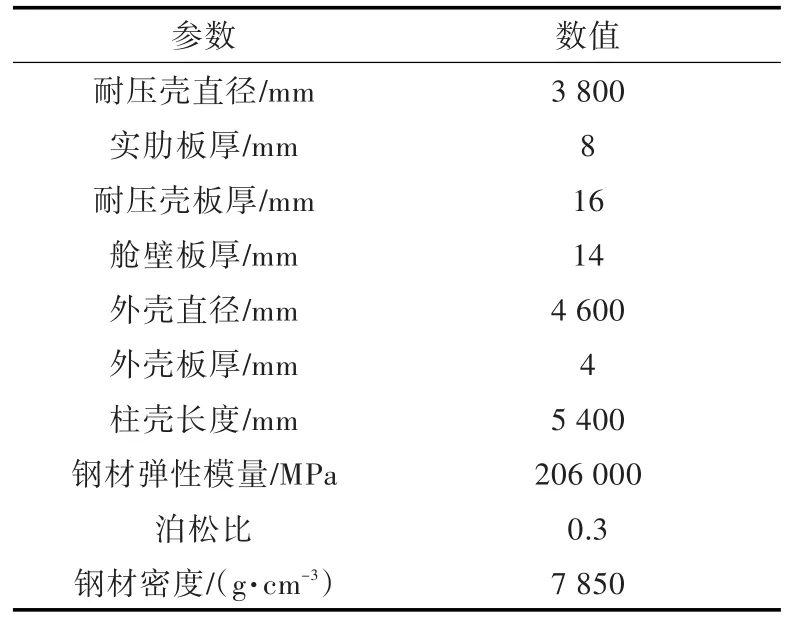
表1 圆柱壳结构参数Table 1 Structure parameters of cylindrical shell model

图2为圆柱壳的SEA模型，根据自然几何边界条件和材料介质特性，以及满足模态相似、弱耦合等条件，将模型划分为21个子系统。耐压壳和外壳分别划分为3个壳体子系统，舱壁划分为2个平板子系统，实肋板划分为8个平板子系统，还有4个声腔子系统和测点处的半无限流域子系统。

模型中所有结构子系统的内损耗因子取0.01，流体介质的内损耗因子由声场的内损耗因子确定：

式中：Ca为声速，在空气中，Ca=343 m/s，在水中，Ca=1 481 m/s；V和S分别为声场的体积和吸声面积；α为平均吸声系数，对于金属壁面，，其中f为频率。

本文采用的2种肋骨的参数如表2所示。

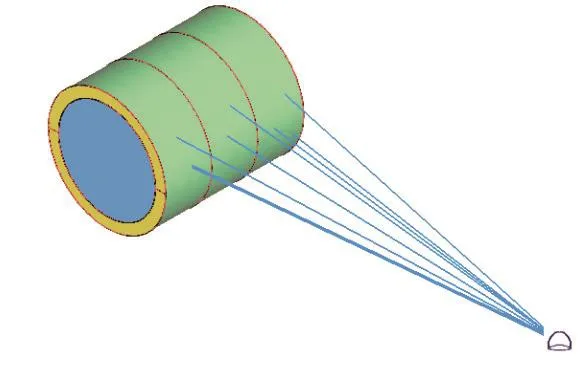
图2 双层圆柱壳的SEA模型Fig.2 The SEA model of double cylindrical shell

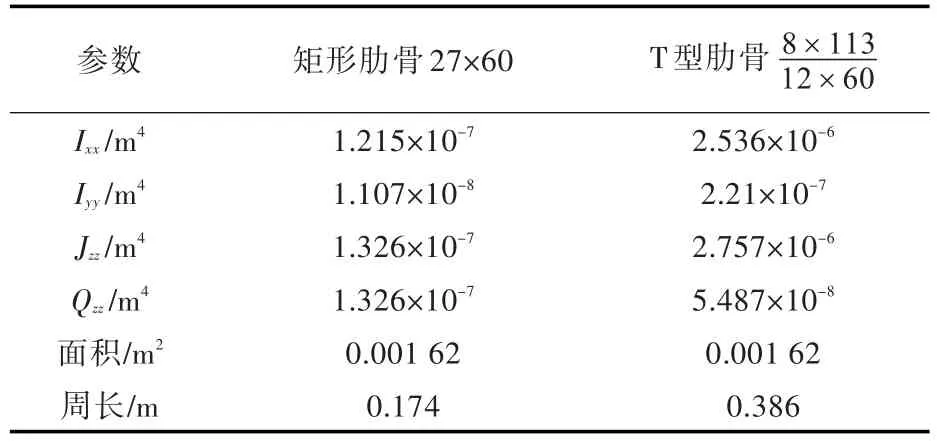
表2 肋骨参数Table 2 Parameters of the ribs

图3为频带内所有子系统的模态数。模型分析频带为500 Hz～100 kHz的1/3倍频程，从图中可以看出，在500 Hz以上时，所有子系统的模态数都大于5，满足采用SEA进行计算时对模态密度的要求。

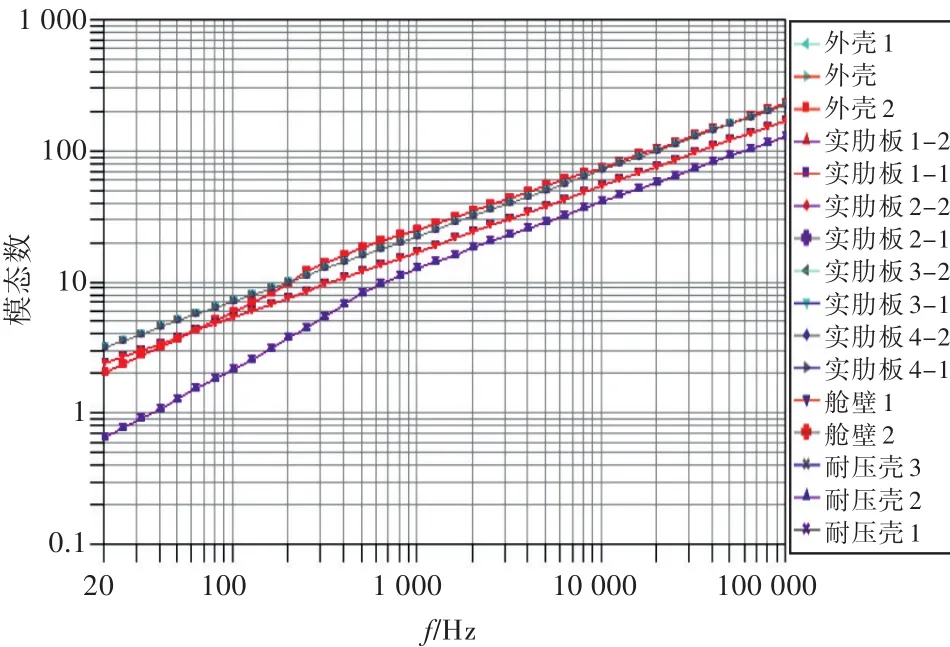
图3 各个子系统的模态数Fig.3 Modal number of subsystems of cylindrical shell

3 肋骨对圆柱壳SEA参数的影响

子系统的SEA参数由每个子系统的波在结构中的传播特性决定［7］，肋骨对圆柱壳的影响体现在对子系统SEA参数的改变。通过分析各项参数的理论公式，并对比AutoSEA2软件的仿真结果，研究肋骨对双层圆柱壳子系统SEA参数的影响。计算时采用矩形肋骨，间距为0.6 m。

3.1 肋骨对模态密度的影响

模态密度是单位频带内子系统的模态数，它反映了子系统贮存能量的能力，是非常重要的SEA参数。模态密度的改变会影响各个子系统间的能量流动，改变结构的振动特性。结构的模态密度与其导纳实部的平均值有关［8］：

孤独，也是精神的境界，孤独是不奢望他人的感同身受，孤独是一种精神上的自立与自我审视，孤独对每个人的成长都有着独特的价值。当杜小康在雨后的夜晚迷路找不到父亲的时候，他的孤独达到了极限，他感觉累极了，他哭了起来。然而他却看见了从未见过蓝成这样的天空，月亮又是那么的明亮。自然以一种神奇的力量考验了这个少年，也慰藉了这个少年，他不再哭泣，他觉得自己突然地长大，坚强了。让少年在成长过程中体验孤独的苦痛与甘美，可以促进少年的精神健康成长。

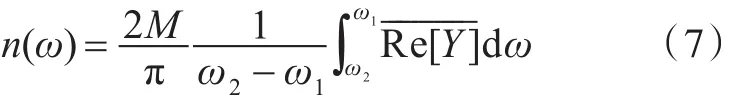
式中：n(ω)为子系统的平均模态密度；M为子系统质量；ω1和ω2分别为频带的上限和下限；Re［Y］为子系统导纳的实部。增加肋骨到圆柱光壳使结构的导纳降低，导致子系统模态密度减小。圆柱光壳增加肋骨前、后的模态密度随频率的变化规律如图4所示。增加肋骨降低了圆柱光壳的模态密度，特别是对于较薄的外壳，增加相同肋骨时，与耐压壳相比，其模态密度大幅降低。

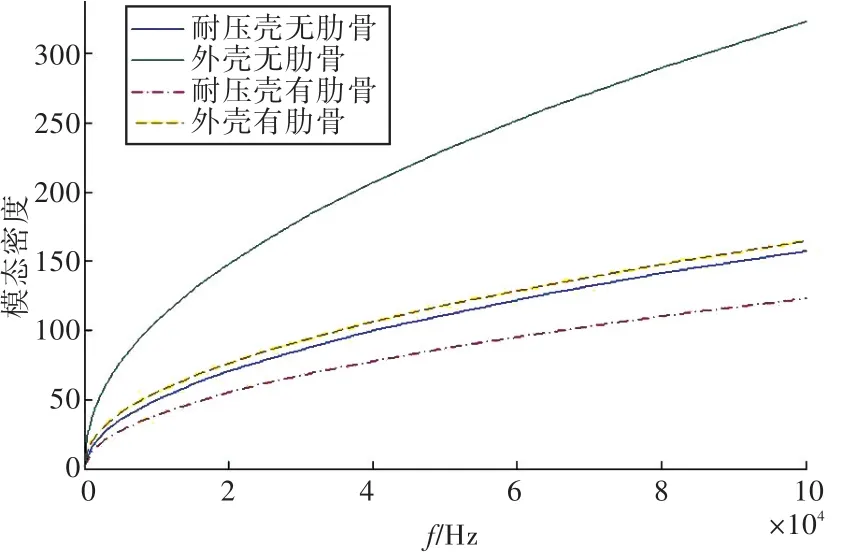
图4 耐压壳和外壳的模态密度变化Fig.4 Variation of modal density of pressure shell and outer shell

3.2 肋骨对耦合损耗因子的影响

相邻子系统i和j之间的耦合因子ηij反映了其耦合程度。对于线连接的结构，其耦合损耗因子可以由2个结构件的传输系数求得［9］：

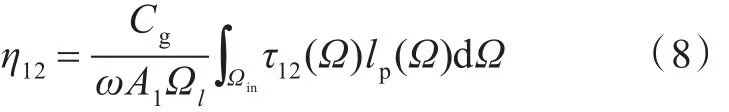
式中：Ω为入射波方向角；Ωl为Ω的取值范围；Ωin为入射角的范围；Cg为结构中弯曲波传播的群速度；A为子系统的面积；lp(Ω)为耦合线在入射波方向上的投影长度；τ12(Ω)为两个子系统间的传输系数。圆柱壳与实肋板之间的传输系数经验 值［6］为τ12=D1/D2（D1＜D2），结 构 刚 度D=ρsR2C2l，其中ρs，R和C1分别为结构的面积质量密度、回转半径和纵向波速。增加肋骨到圆柱壳改变了其刚度，从而改变了圆柱壳与实肋板间的传输系数，导致子系统间耦合损耗因子的改变。

增加肋骨之后，相邻外壳之间以及外壳与实肋板之间的耦合损耗因子随频率的变化规律如图5所示。由图可见，实肋板与圆柱壳之间的耦合损耗因子减小；2个外壳之间的耦合损耗因子也减小。实肋板与圆柱壳之间、相邻圆柱壳之间的耦合程度降低。

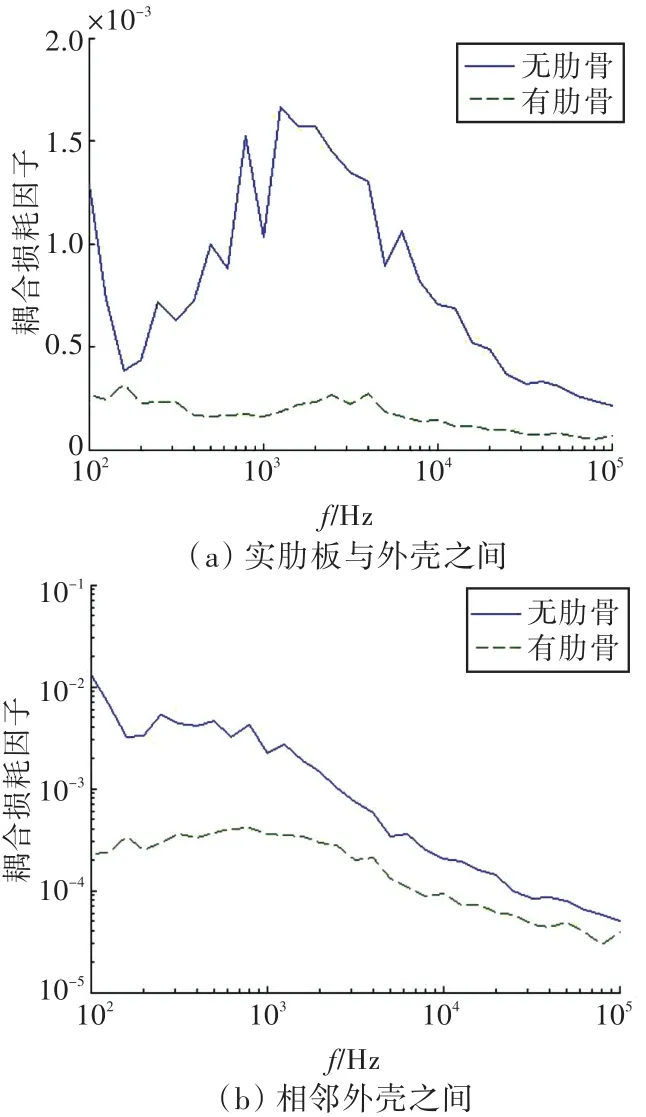
图5 耦合损耗因子随频率的变化规律Fig.5 Variation of coupling loss factor with frequency

3.3 肋骨对辐射比的影响

辐射比的定义为

式中：prad为结构的辐射功率；，为具有相同面积、相同均方根速度的刚性平板辐射功率。辐射比反映了结构向流场辐射噪声的能力。圆柱壳的辐射比为

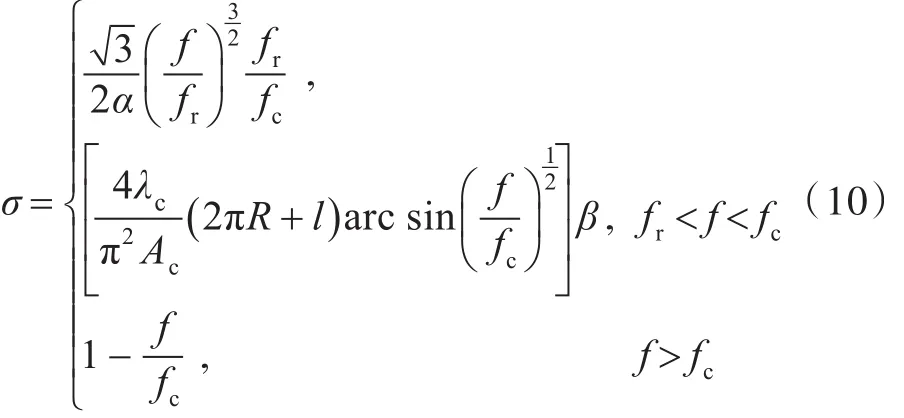
其中，

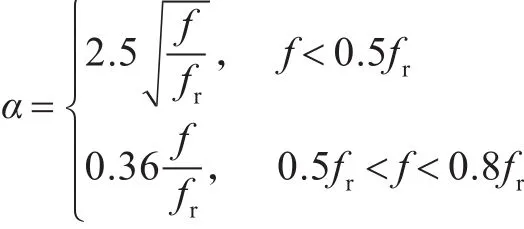
式中：λc为fc对应的声波波长；Ac为圆柱壳表面积；l为加强件长度；R为圆柱壳半径；fr为环频率；fc为临界频率；β为系数，与边界条件有关，简支边界β=1，固定边界β=2，一般边界β= 2。

图6为双层圆柱壳外壳增加肋骨前、后外壳的辐射比随频率的变化规律。增加肋骨使结构的临界频率fc增大，根据式（10）可得，在临界频率之前，fc增大导致辐射比减小；在临界频率之后，fc增大导致辐射比增大。

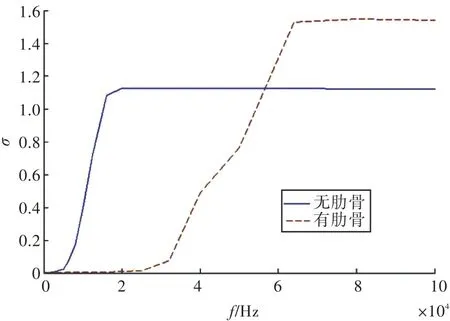
图6 外壳的辐射比Fig.6 Radiation ratio of outer shell

3.4 肋骨对输入功率的影响

当激励源是点源，并且为理想力源时，激振力对结构的平均输入功率为

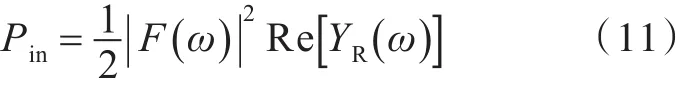
式中：F为激振力；YR为输入导纳。增加肋骨到圆柱光壳降低了其输入导纳，在同样的激振力下，输入功率降低。双层圆柱壳增加肋骨前、后输入功率随频率的变化规律如图7所示。从图中可以看出，有肋骨时，激振力的输入功率在整个频带上都有所下降，并且与无肋骨相比曲线更加平滑。因为增加肋骨后，肋骨降低了圆柱壳的导纳，抑制了结构的振动，结构对激振力的响应减小，并且随频率的改变更加平缓，因此输入功率曲线更加平滑。

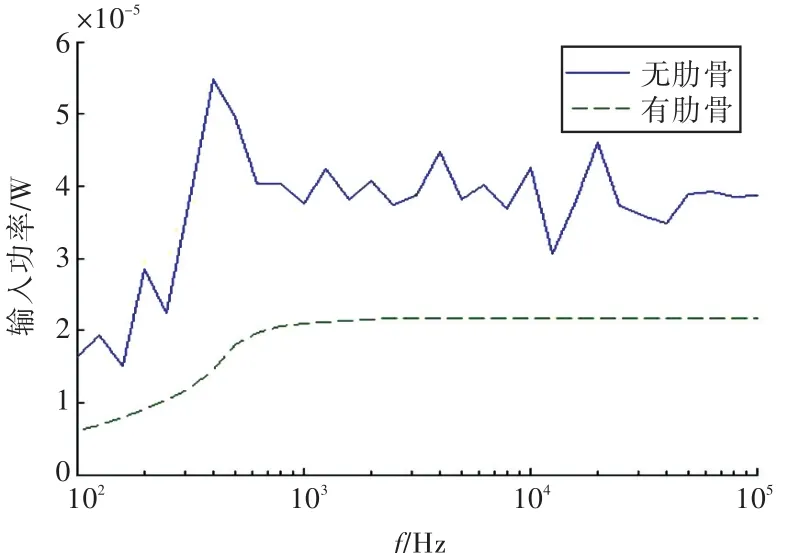
图7 耐压壳的输入功率Fig.7 Input power of pressure shell

4 不同肋骨参数对双层圆柱壳声辐射特性的影响

肋骨改变了结构的刚度和重量，从而也改变了结构的动态响应特性［10］。对于均匀厚度的各向同性壳体，加强肋和筋的作用是引起自由弯曲波的散射，从而改变结构的共振频率和模态形状，这可以显著改变结构的振动和声辐射特性。基于第3节得到的SEA参数变化规律和AutoSEA2软件的计算结果，对比肋骨参数不同时双层圆柱壳的辐射声压级和外壳振动均方根速度，研究肋骨参数对双层圆柱壳声辐射特性的影响。得到了耐压壳、外壳分别增加肋骨时，不同肋骨间距和不同肋骨形状下双层圆柱壳声辐射特性的变化规律。

4.1 耐压壳和外壳分别增加肋骨对双层圆柱壳声辐射特性的影响

计算耐压壳和外壳分别增加肋骨时的外壳平均振速和15 m处的辐射声压级，采用矩形肋骨，肋骨间距为0.6 m，结果如图8所示（参考声压Ref=10-6）。

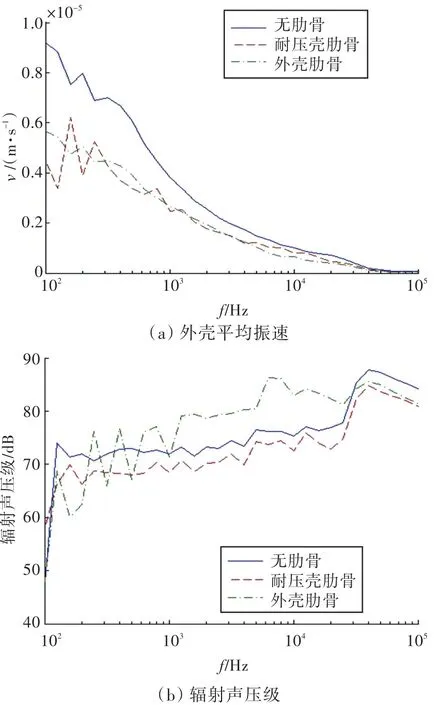
图8 外壳振速和圆柱壳辐射声压级Fig.8 Vibration velocity of outer shell and sound pressure level of cylindrical shell

由图8（a）可知，肋骨加在耐压壳和外壳上时均能减小外壳的振动，并减振效果基本相同。由前述分析可得，肋骨加在耐压壳上时，可以减小输入功率并且减少能量通过实肋板向外壳的流动，从而减小外壳的振动；肋骨加在外壳上时，可以直接抑制外壳的振动。

由图8（b）可知，肋骨加在耐压壳上时，圆柱壳的辐射声压级下降了5 dB左右。当肋骨加在外壳上，在环频率以下和临界频率以上时，圆柱壳的辐射声压有所降低；在环频率和临界频率之间时，圆柱壳的辐射声压反而明显增大。根据第3节的分析，在外壳增加肋骨时，虽然外壳的振动速度降低了，但是增加肋骨会改变其辐射比，从而导致辐射噪声增大。

由此可得，在肋骨相同的情况下，在耐压壳上增加肋骨比在外壳上增加肋骨更能降低双层圆柱壳的辐射噪声。

4.2 肋骨间距对双层圆柱壳辐射声压级的影响

改变耐压壳的肋骨间距，计算不同肋骨间距时的圆柱壳辐射声压级。采用的肋骨为矩形肋骨，间距分别为0.9，0.3和0.1 m，计算结果如图9所示。从中可以看出，随着肋骨间距的减小，辐射声压级在整个频带上随之减小。减小肋骨间距可以减小耐压壳的模态密度，减小激振力的输入功率，并且降低能量向外壳的流动，从而减小外壳的振动速度；因此，减小肋骨间距可以一定程度上降低圆柱壳的辐射噪声。

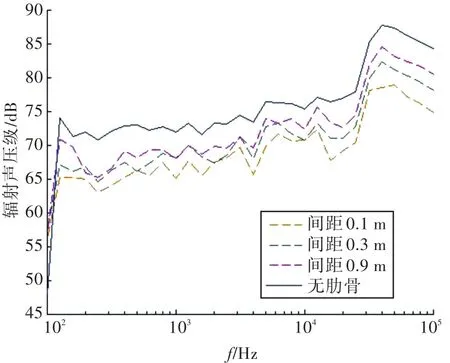
图9 不同肋骨间距的辐射声压级Fig.9 Radiation sound pressure level with different rib distances

4.3 肋骨形状对双层圆柱壳辐射声压级的影响

在截面积相同的情况下，肋骨截面形状不同，对结构振动与辐射噪声的影响可能不同。计算耐压壳肋骨分别为矩形肋骨和T型肋骨的辐射声压级，不同形状肋骨圆柱壳的辐射声压级随频率的变化规律如图10所示。从中可以发现，虽然2种肋骨形状不同，面积惯性矩相差很大，但是2种肋骨对应的辐射声压值基本一致，差异非常小。可见肋骨形状对圆柱壳辐射噪声的影响不大。

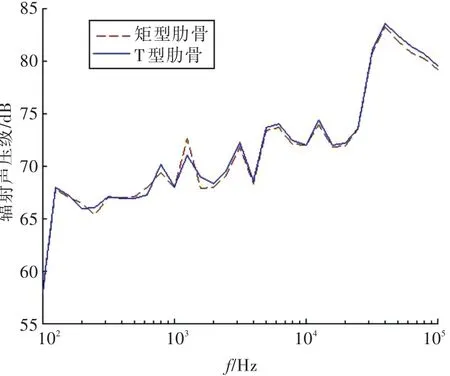
图10 不同肋骨形状的辐射声压级Fig.10 Radiation sound pressure level with different rib shapes

4.4 激振力作用位置对声辐射特性的影响

对于环肋圆柱壳，激振力可能作用在壳体上，也可能作用在肋骨上。激振力作用在不同位置时，由于激振点的阻抗不同，肋骨的降噪效果有所不同。研究激振力作用位置不同时肋骨的降噪效果，可以为水下航行器的设计提供一定的参考。

分别计算激振力作用在肋骨上和肋骨间时双层圆柱壳的辐射声压级，结果如图11所示。由图可知，在低频段，不管激振力作用在肋骨上还是作用在肋骨间，肋骨对双层圆柱壳声辐射特性的影响基本相同；在高频段，随着频率的增大，激振力作用位置不同时，肋骨对声辐射特性的影响也不同。当激振力作用在肋骨间时，随着频率的增大，肋骨的作用慢慢降低，辐射声压级逐渐趋于无肋骨的情况；当激振力作用在肋骨上时，随着频率的增加，肋骨的作用更加明显，辐射声压级降低更多，这是因为当激振力作用在肋骨上时，激振点的阻抗更高。

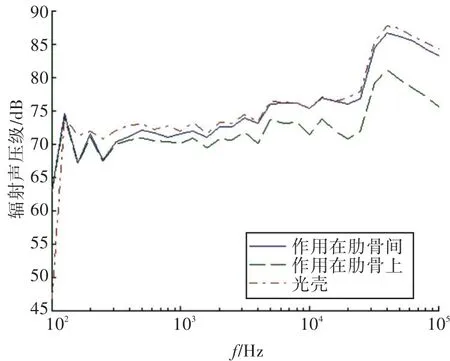
图11 不同激振力作用位置的辐射声压级Fig.11 Radiation sound pressure level with different locations of excitation forces

5 结 论

本文运用统计能量法研究了肋骨参数对环肋双层圆柱壳声辐射特性的影响，得到如下结论：

1）在耐压壳增加肋骨时，外壳的振动速度和双层圆柱壳的辐射声压级都有所下降。

2）在外壳增加肋骨时，虽然外壳的振动速度明显降低，但双层圆柱壳的辐射声压级下降较少，在某些频带内，辐射声压级甚至大于不加肋骨的情况。

3）在耐压壳增加肋骨比在外壳增加肋骨更有利于降低舱段的辐射噪声。

4）肋骨形状对舱段辐射噪声的影响很小，在选择肋骨形状时，可以只考虑结构要求，忽略其对辐射噪声的影响。

5）当激振力作用在壳体上时，随着频率的增大，肋骨的作用慢慢降低，逐渐趋于无肋骨的情况；当激振力作用在肋骨上时，随频率的增大，肋骨的作用更加明显。