全桥LLC电路时域模型及其分析
王志刚, 董长城, 侯 凯, 高鹏飞
(1. 南瑞集团(国网电力科学研究院)有限公司, 江苏省南京市 211106;
2. 国电南瑞科技股份有限公司, 江苏省南京市 211106; 3. 河海大学能源与电气学院, 江苏省南京市 211100)
0 引言
由于LLC谐振电路能够同时实现隔离变压器原边和副边的功率器件的软开关效果,具有高效率和高功率密度的优势,被广泛应用于DC/DC变换器场合[1-2]。传统的LLC电路分析方法为频域分析方法,基于基波近似法(FHA)简化模型虽然可以非常方便地绘制增益曲线和进行相应的参数设计,但是这种分析方法却忽略了高频分量对电路设计过程中的影响,而且不能反映电压和电流在某一个点上的时域状态。
文献[3-4]基于时域分析方法分析电路,给出每个阶段的时域方程,但是仅关注开关频率小于谐振频率的升压部分,也未根据这些时域方程的相互关系,推导出包含电路全部信息的方程组。文献[5]在进行时域分析时对谐振电流进行了简化,导致在远离谐振点处会造成较大偏差。文献[6]在FHA频域分析模型的基础上引入时域分析方法,重新定义增益公式中相关部分为谐振因数和负载因数进行分析,但是这种定义没有明确的依据,且缺乏现实的物理意义。文献[7-9]只是针对LLC电路的移相控制部分进行了时域分析,而未对占LLC电路绝大多数的工作状态的变频工作部分进行时域分析。
因此本文根据全桥LLC电路的时域电压、电流波形,分段推导出包含电路工作时全部信息的时域方程组。在方程组的基础上,根据边界条件,求解出其数值解,包括增益、瞬时电压和电流等,并且与FHA作了对比分析。
1 LLC电路拓扑和工作区域
全桥LLC电路的拓扑示意图如附录A图A1所示。其中:S1至S4为4个具有反并联二极管的开关管;D1至D4为输出整流二极管;Co为输出滤波电容;RLd为负载;n为原副边匝比;谐振元件包括电感Lr(包括变压器的原边漏感)、Lm和电容Cr,其中Lr和Cr分别为谐振电感和谐振电容,而Lm与变压器并联,可以由变压器的励磁电感来实现;由于谐振电容Cr串联在原边回路中,它同时起到隔直作用。
根据电压增益和电路频率将全桥LLC电路工作区域分类,如附录A图A2所示。其中区域3为容性工作区域,此时开关管无法实现零电压开关(ZVS)开通,损耗大且频率太低,不利于变压器设计,一般LLC电路不工作在此区域。因此本文只讨论区域1和区域2全桥LLC电路工作状态。
2 LLC电路全时域方程
2.1 区域1全时域方程
区域1:在工作频率fs>fr(Lr和Cr的谐振频率)时,电压增益小于1.0,处于降压模式[10],变换器呈感性,开关管工作在ZVS开通状态。区域1的工作波形如图1(a)所示,根据电压、电流实际工作波形对电路进行分析,可建立全时域方程组。其中vgs1,2,3,4为S1至S4的驱动信号,vAB为开关管H桥中点输出电压,iLr为谐振腔电流,vLr为谐振电感上的电压,iLm为励磁电流,vCr为谐振腔电容电压,iCr为流经谐振电容的电流,iD1为流经二极管D1的电流,iD3为流经二极管D3的电流,Vi为LLC输入端直流电压,Vo为LLC输出端直流电压。
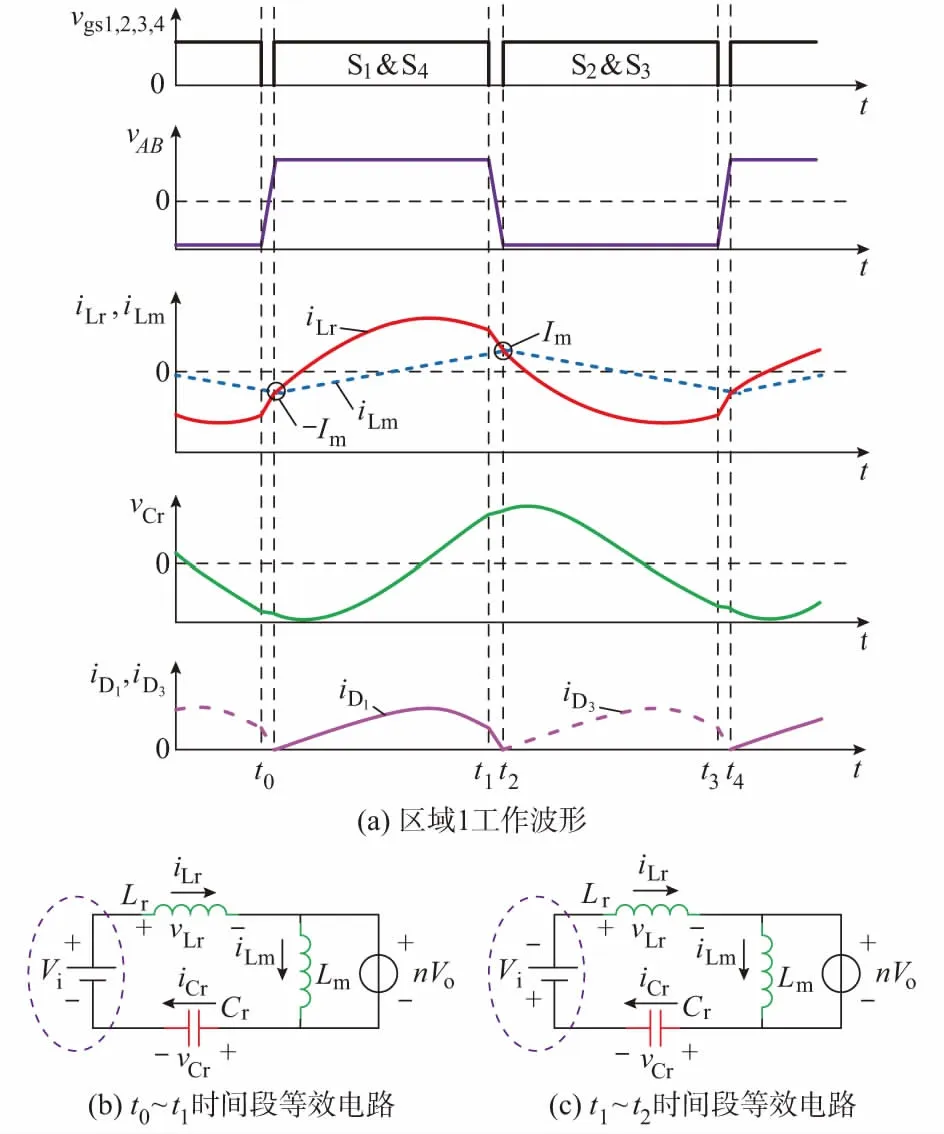
图1 区域1工作波形及半周期等效电路图Fig.1 Working waveform of area 1 and equivalent circuit in half cycle
死区时间对LLC电路实现ZVS开通有一定影响,在电路特性分析中视情况区分对待。对于区域1,因谐振电流不能突变,如图1(a)中t1~t2死区时间内谐振电流逐步下降至励磁电流,因此死区时间不能直接忽略。而为了方便分析,认为在t1时间点,vAB电压直接反向。那么在区域1内,谐振等效电路如图1(b)和图1(c)所示。在t0~t1时间段内,vAB等于Vi,电流方向如图1(b)所示。在t1~t2时间段内,vAB等于-Vi,电流方向保持原有方向,如图1(c)所示。
记t0时间为开始时刻,根据图1(b)和图1(c)等效电路,可列写微分方程组如式(1)所示。
iLr(t)=Csin(w1t+φ)=Ccosφsin(w1t)+
Csinφcos(w1t)
(1)
式中:iLr(t)为iLr瞬时值,其他带有后缀(t)的变量同样表示此变量的瞬时值;C和φ为常量;w1为谐振电流的角频率。
记将初始条件式(2)代入式(1)中可以得到:
(2)
(3)
式中:Im为t=t2时的谐振电流值。
由稳态时波形的对称性可知,t=t0时的谐振电流值为-Im。对应于图2(a),Im为t=t3时的谐振电流值。vCr(0)为t=t0时的谐振电容上的电压,记为其初值。
根据基尔霍夫电压定律对等效电路进行分析可得:
vCr(t)= (Vi-nVo)-[(Vi-nVo-
vCr(0))cos(w1t)+w1LrImsin(w1t)]
(4)
在上述分析的半周期内,励磁电流iLm为线性变化,结合得到的电流iLr和电压vCr表达式可得:
(5)
为便于对LLC电路变量分析,将相关参量进行归一化处理[9,11-12],设置基准电压VB、基准电流IB、基准阻抗ZB和基准角频率wB如式(6)所示。
(6)
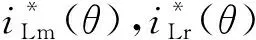
1)0≤θ≤θ1
(7)
2)θ1≤θ≤θ2
(8)
2.2 区域2全时域方程
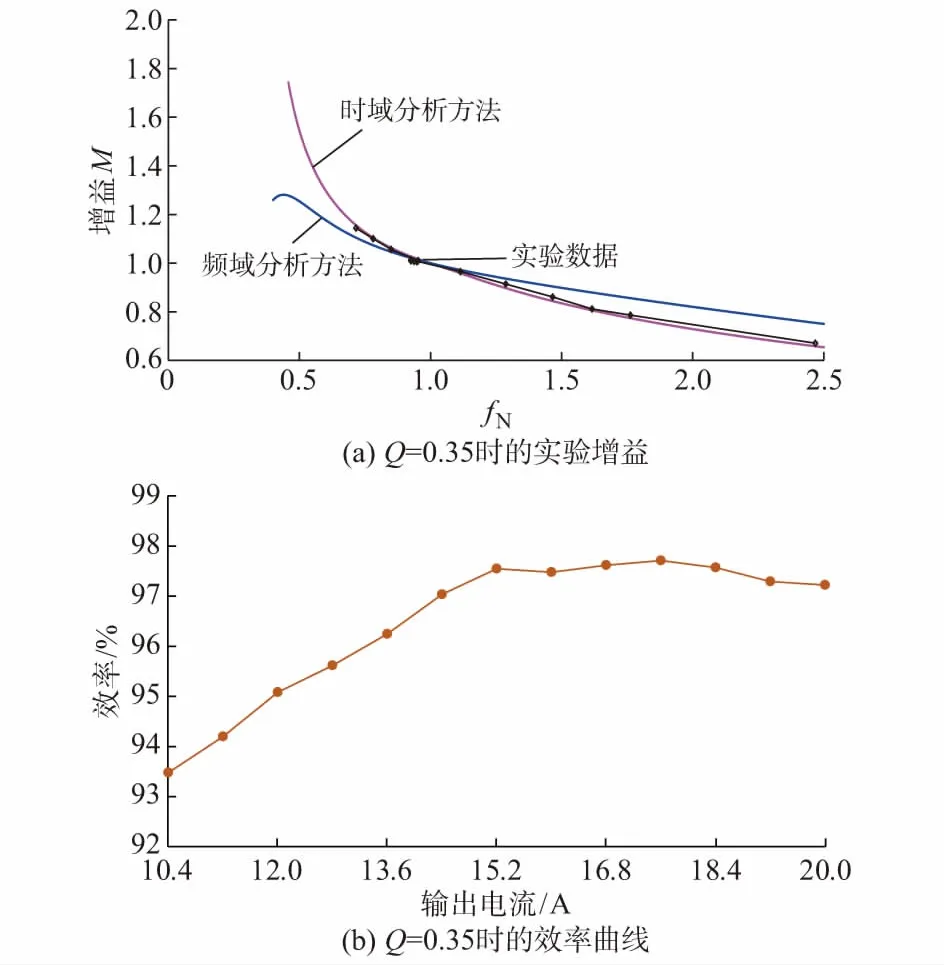
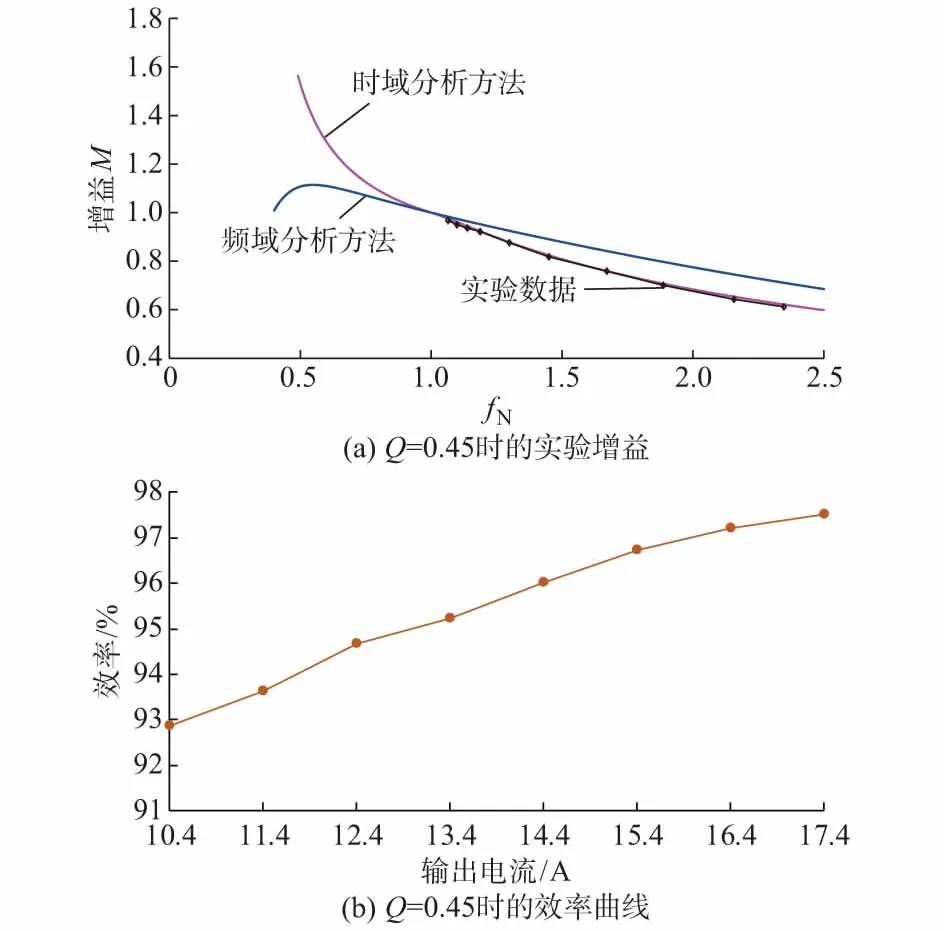
区域2:在fs 图2 工作区域2半周期等效电路图Fig.2 Half Equivalent circuit of area 2 in half cycle 类似区域1分析过程,对区域2的等效电路进行分析得到时间段t0~t1和t1~t2的励磁电流iLm、电流iLr和电压vCr,然后将时间段转化成角度段0~θ1和θ1~θ2并且将电压电流量标幺化得到式(9)和式(10),即 1)0≤θ≤θ1 (9) 2)θ1≤θ≤θ2 (10) 2.1节和2.2节根据LLC电路工作区域1和2的电压电流波形列写了其时域方程。时域方程反映了各部分电压电流的瞬时值,但是方程中有一些参数需要通过一些边界条件进行限定[13-14]。 对于区域1,边界条件为: (11) 同时根据励磁电流iLm从t0积分到t2为零,根据文献[8]可得: (12) 式中:品质因数Q=Zr/[(8n2/π2)RLd],其中RLd为输出端等效负载电阻,Zr为特征阻抗。 基坑与斜拱桩基承台边缘净距不同时,斜拱桩基产生的水平推力对深基坑的影响是不同的。分析边缘净距L对邻近深基坑围护桩的影响时,斜拱桩基先于深基坑施工,即基坑开挖前斜拱已经对承台施加荷载。边缘净距L分别取为5 m、10 m、15 m、20 m、25 m、30 m。图6和图7分别为不同边缘净距下围护桩桩身最大水平位移分布图和围护桩最大水平位移变化曲线图。 综上所述,联立所有边界条件和约束条件可得: (13) 对于区域2,边界条件为: (14) 区域2的不同之处的是励磁电流从t0到t2并不是一条直线且其积分不为零。由t0到t2的积分与输出电流的Io的关系可以推出: (15) 因此类似区域1情况,联立所有边界条件和约束条件可得方程组如式(16)所示。 (16) 上文给出了包含LLC电路完整时域信息的隐式方程组,为进一步进行分析,并验证时域分析的有效性,本章使用数学工具MATLAB软件,通过fsolve(·)函数计算出方程的数值解。fsolve(·)解决的方程形式为F(X)=0,用法为: x=fsolve(f(x),x0) (17) 式中:f(x)为方程组;x0为初值,需要提前设定。 求解过程中最重要的是确定迭代算法和初值,迭代算法使用“信赖域狗腿法(trust-region-dogleg)”,这种最优化算法的优点是可靠性高,有效性和收敛性强。首次初值的设定,根据LLC电路实际工况和参数进行设定,因谐振点处的工作状态最为简单,并且参数估算最为容易,所以选取谐振点处的电气参数为首次计算的初值,然后通过fsolve(·)函数求解谐振点处的各个变量的真实值,此为一次完整的求解过程。 以此类推,进行其他工作频率点的方程的求解。 图3 时域与频域增益曲线比较Fig.3 Comparison of gain curves in time domain and frequency domain 对于FHA增益曲线,许多论文提及增益最高点是感性和容性工作区域的分界点,但是根据图3(b)可知,此分界点位于B点,要略小于增益最高点A点。这是因为FHA实际上是有损分析,丢失了一些高频分量的影响。所以基于FHA的电路设计中,要保证电路实现ZVS开通的效果,增益一般要取0.9~0.95的裕度。 为对所建立的时域模型进行验证,在20 kW电动汽车充电模块[7]上对增益特性进行了实验分析。实验电路为双路输入串联输出并联(ISOP)型LLC电路,下面的实验分析只针对单路,实验工作波形如附录A图A3所示。 针对特定的Q,施加一定的电阻负载,同时测量单路LLC电路的输入电压和输出电压,然后计算输出电压与输入电压的比值,获得真实增益。并将通过频域分析方法(FHA)、时域分析方法和实验方法获得的增益曲线绘制在一起,如附录B表B1和图4所示。同理可绘制出Q=0.35和Q=0.45时的增益曲线和效率曲线,如图5和图6所示。 由实验结果可知,相对于FHA,时域分析方法获得增益更加贴近实验数据,尤其是工作频率小于谐振频率时。工作频率大于谐振频率时,随着Q变小,即负载变轻时,高频段的实测增益有上翘趋势,时域分析方法的增益曲线较实验数据偏差变大。另外从效率曲线可以看出,高频段LLC的效率下降较快,理论上会对增益造成一定的损失,但是由于高频段曲线上翘,并不十分明显。有关高频段增益上翘的现象将在后续研究中进行分析。 图4 Q=0.25时增益及效率Fig.4 Gain and efficiency when Q=0.25 图5 Q=0.35时增益及效率Fig.5 Gain and efficiency when Q=0.35 图6 Q=0.45时增益及效率Fig.6 Gain and efficiency when Q=0.45 本文建立了完整的全桥LLC时域分析模型,建立了其时域非线性方程组,给出了其求解方法,并针对软开关范围和增益进行了详细的分析。增益实验证明,本文所提时域模型及分析方法能够更为准确地表述LLC电路的特性,尤其远离谐振点时的电路特性。时域分析方法设计非线性方程组,较FHA方法更为复杂,如何将其工程实用化是以后研究工作的重点和难点。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。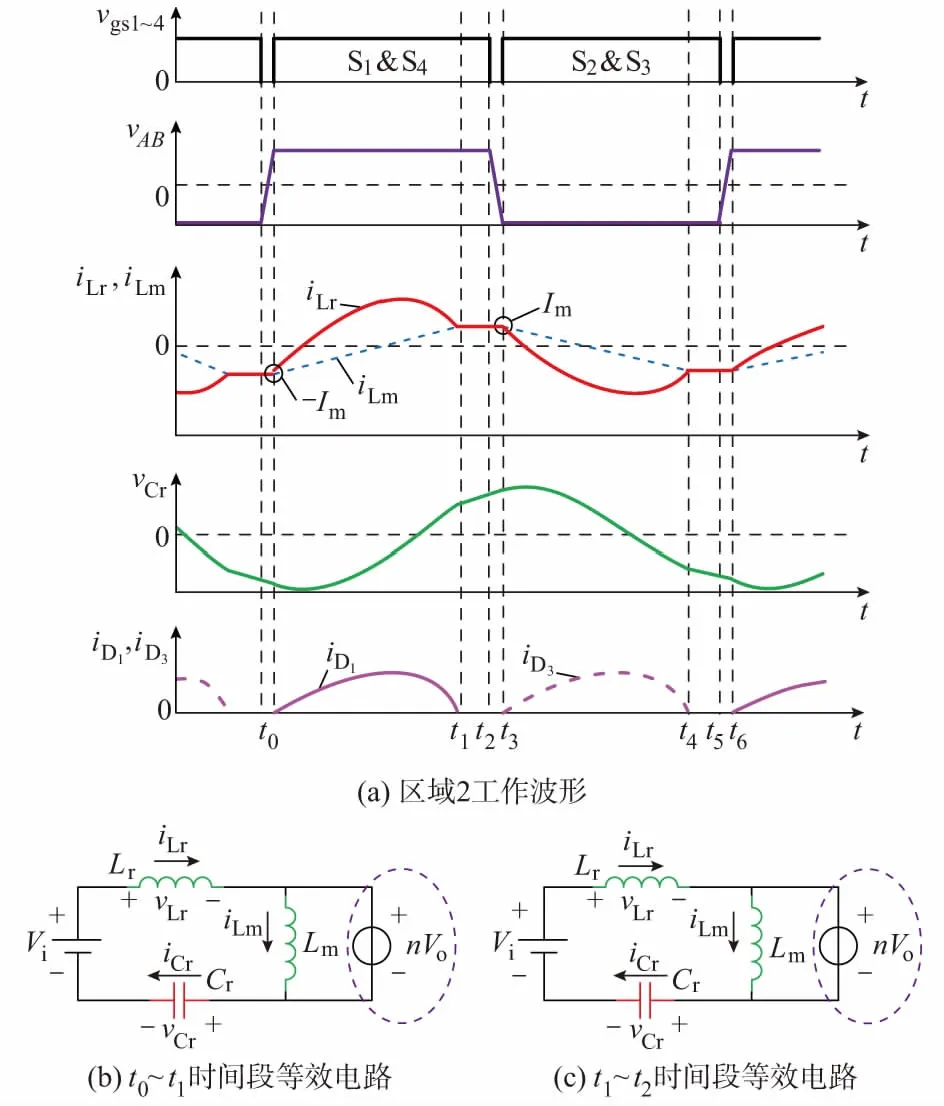
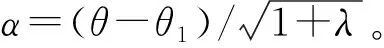
2.3 边界条件及非线性方程组
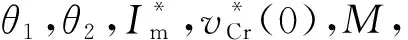
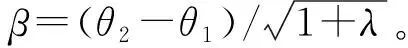

3 分析与实验
3.1非线性方程求解
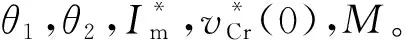
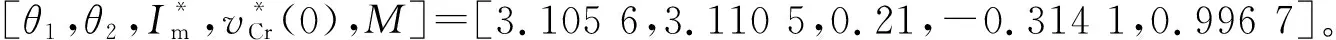
3.2 软开关分析
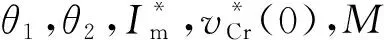
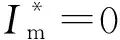
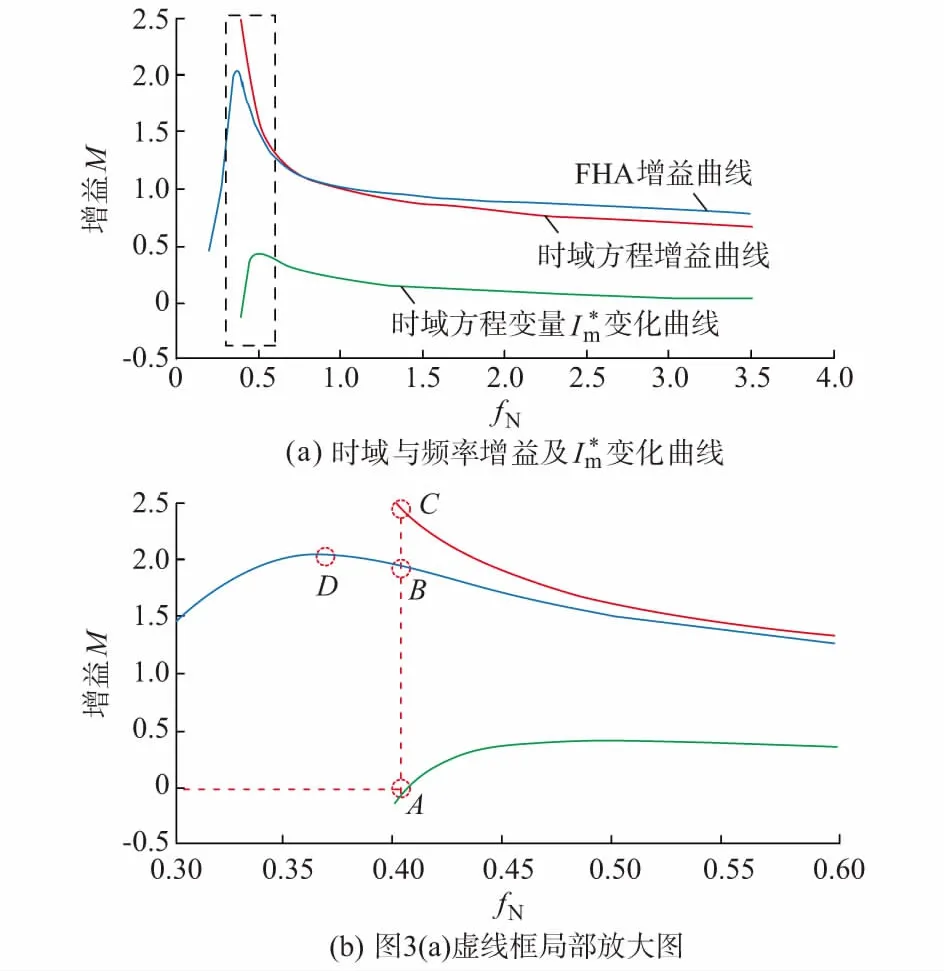
3.3 实验
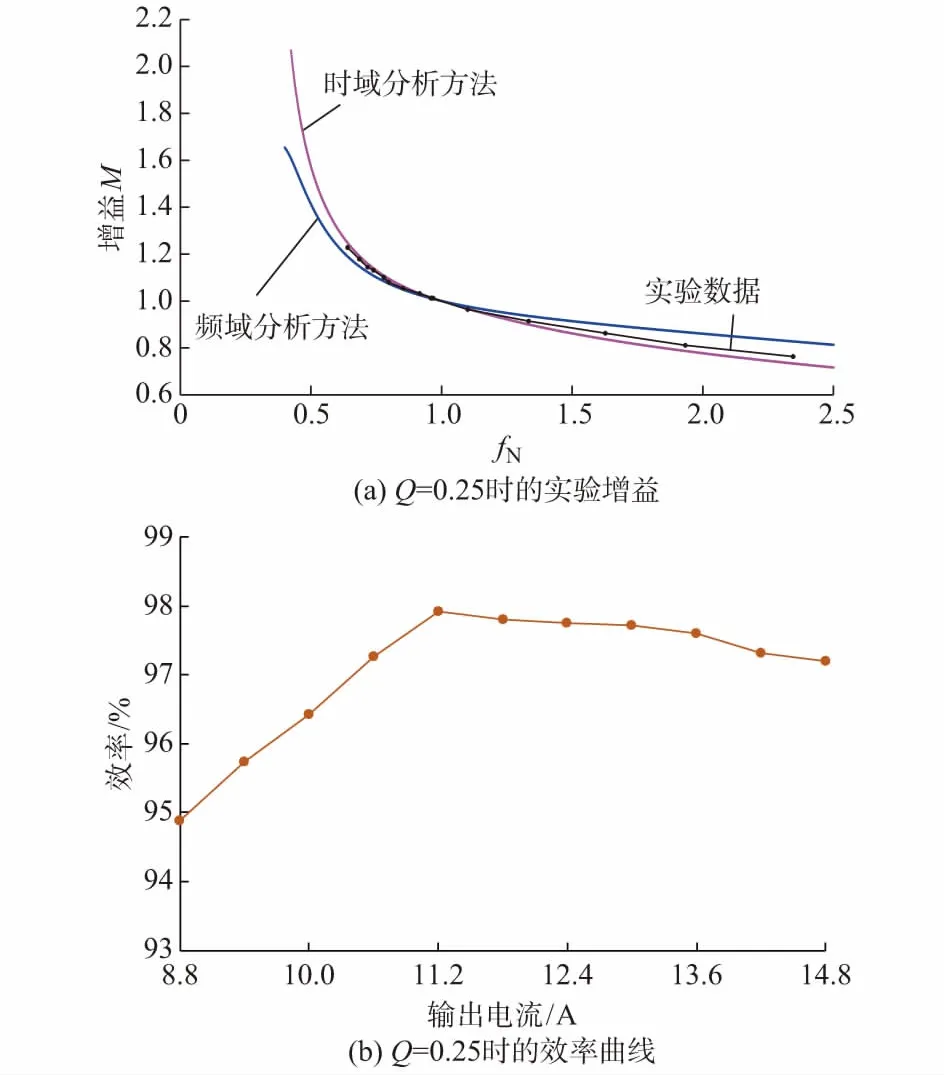
4 结语

