计及热惯性和运行策略的综合能源系统可靠性评估方法
吕佳炜, 张沈习, 程浩忠
(电力传输与功率变换控制教育部重点实验室(上海交通大学), 上海市 200240)
0 引言
在传统化石能源储量有限和环境污染问题日益严重的双重压力下,粗放的能源利用模式与环境保护之间的体制机制性矛盾日益凸显。在此背景下,得益于能源转换技术的不断发展,综合能源系统(integrated energy system,IES)应运而生。IES是指在规划、设计、建设和运行过程等过程中,通过对各类能源的产生、分配、转换、消费、存储等环节进行有机协调与优化后,所形成的能源产供消一体化系统[1-2]。然而,IES设备种类繁杂,运行特性各异,同时伴随着能量的双向流动,使得其可靠性的评估更为复杂[3-4]。
当前,针对IES可靠性评估问题,国内外的研究主要集中在电—气或冷—热—电这两类能源系统。文献[5]建立了燃气—电力互联系统的可靠性模型,计算了联合循环发电厂可提供的最大电量。文献[6]以能源集线器模型为基础,提出了一种IES可靠性评估方法。文献[7]利用马尔可夫模型对建筑中冷—热—电联产系统的可靠性进行了量化分析,证明了冷—热—电联产对提升系统可靠性的积极作用。文献[8]采用模块化建模方法,对冷—热—电系统进行仿真分析,证明了基于微型燃气轮机的热电联产对提高系统可靠性的积极作用。文献[9]将概率潮流思想用于IES概率能流分析中,分析了电力系统和天然气系统中不确定因素对IES运行的影响。文献[10]提出了一种考虑负荷随机性和能源品味差异的综合能源系统可靠性评估方法。文献[11]提出了计及可靠性的电—气—热能量枢纽配置模型,计算了能源枢纽最优容量配置。上述研究表明,IES的可靠性评估已受到国内外学者的广泛关注,但仍然存在以下问题:①当前研究大多从稳态角度分析系统可靠性,对多时间尺度下的评估仍然不够完善;②现有可靠性评估方法只考虑了元件故障情况,而在实际运行过程中,能源品味差异和系统运行策略等因素对可靠性也有较大影响。因此需要基于时间尺度差异、能源品味差异和系统运行策略,展开IES的可靠性评估。
本文首先分析了多能互济机制,把IES等效为不同能流相互联络的互联系统,推导出能流互济可靠性增益这一指标。其次,对热惯性进行准稳态建模,根据能源品味差异设置系统运行基本策略,通过基于马尔可夫链的蒙特卡洛模拟方法计算IES的可靠性。最后,通过实际算例进行仿真分析,验证本文所提模型、指标、方法的有效性。
1 能流互济的可靠性增益
IES能流互济的本质是充分利用不同形式能源的互济能力对各环节协同优化,以提升系统可靠性。基于此,本节提出了能流互济可靠性增益的概念及其计算方法。
1.1 能源集线器模型
为描述IES中不同能流的协同运行机制,文献[12-13]引入了能源集线器模型以刻画不同形式能源的耦合关系。在该模型下,IES被抽象为包含多种形式能源输入、能源转换设备集和多种形式能源输出的双端口网络。
能源集线器模型可分为“配—转—用”三部分,定义耦合矩阵C表示能流转换过程以描述三者的关系。
L=CE
(1)
即
式中:α,β,,ω分别代表不同能源种类。E和L分别为能流输入和输出矩阵;C为耦合矩阵,包括能源转化效率和优化调度因子。用i和j表示能流转换路径,i,j∈{α,β,,ω}
1.2 能流互济可靠性增益
相比独立运行的传统能源系统,IES具有多能互济的特征,即对于给定的用户需求,其能源输入可能并不唯一。从可靠性角度看,多能互济的本质就是不同形式的能源子系统通过能源转换设备形成了互联系统,各子系统的可靠性较孤立运行时均有提升。计算不同子系统的可靠性指标,通过可靠性二维概率数组图[14]可直观表示能流互济的可靠性增益,如图1所示。
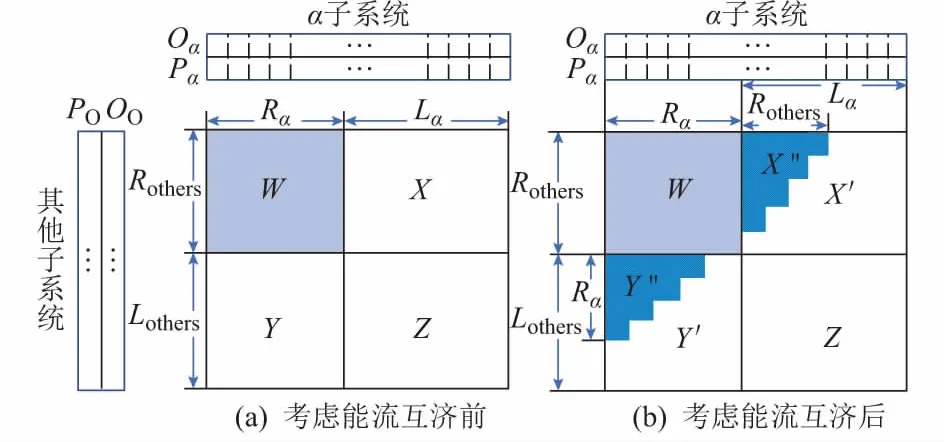
图1 系统可靠性二维概率数组图Fig.1 Diagram of two dimensional probability for system reliability
图1(a)为考虑能流互济前系统可靠性的二维概率数组图。Oα和Pα分别表示α子系统的停运容量和对应概率,OO和PO分别表示其他子系统的停运容量和对应概率,Lα和Rα分别表示α子系统的最大负荷和备用容量,Lothers和Rothers分别表示其他子系统的最大负荷和备用容量。图中阴影部分W区域表示α子系统和其他子系统的停运容量均未超过各自备用容量,IES正常工作;X区域表示α子系统停运容量超出备用,其他子系统正常工作;Y区域表示其他子系统停运容量超出备用,α子系统正常工作;Z区域表示两子系统停运容量均大于各自备用容量。考虑能流互济后,当某一子系统供能不足,可通过能源转换设备接受其他子系统的支援。假设能源转换设备容量和相互支援容量无限制,则系统可靠性的二维概率数组图如图1(b)所示。
对比图1(a)和(b)的阴影部分可知,IES正常工作的区域增加了X″和Y″部分,其中X″部分表明当α子系统停运容量超出备用容量时,其余系统将通过能源转换设备进行支援,提高α子系统可靠性。因此在考虑能流互济后,不同子系统之间能够相互支援,系统备用容量变大,IES可靠性得到了阶梯形的增益。
在实际运行过程中,应考虑支援容量的限制。支援容量受设备限制,定义最大转换容量矩阵ξmax来表征能源转换设备最大转换容量。
(2)
式中:ξij,max表示将能流i转换为j的能源转换设备的最大转换容量,其中i,j∈{α,β,,ω}。
考虑到不同运行策略下,各子系统的重要程度不同,支援优先顺序不同,各子系统可获得的支援容量为:
(3)
式中:ξsup,α为系统α可获得的支援容量;ρiα表示从能流i到α的转换设备工作状态,ρinput,i为能流i输入状态,ρiα,ρinput,i∈{0,k1,k2,,kn,1},0表示设备故障,kn为降额运行系数,1表示设备正常工作;ξiα,max为最大转换容量;Ei为能流i输入容量;Li为能流i输出容量;Siα为优先等级高于α的子系统所需的支援容量,优先级由运行策略决定;ηiα为能源转换效率。
综上,各子系统的能流互济可靠性增益为:
ΔPα=P(L>min{ρinput(Lα+Rα),ρααξαα,max})-
P(L>min{ρinput(Lα+Rα),ρααξαα,max}+ξsup,α)
(4)
式中:ΔPα为能流互济可靠性增益;ξαα,max为同种能流转换设备的最大转换容量;L为子系统实际负荷。
2 热惯性模型
IES中不同能源的传输特性和时间尺度不同。例如电能传输可在瞬时完成,其状态变化处于同一时间断面;而热能传输速度慢,能量的传输和变换横跨多个时间断面,因此,不同能源中断供应后对用户造成的后果也将不同。当各子系统独立运行时,电能供应中断将立刻导致用电设备停运,不能满足用户需求;冷、热等惯性较大的负荷,其用能本质是在一段时间内获得或保持一定温度,即允许温度在一定范围内波动[15],因此,用户对于供能中断的反馈具有滞后性。
图2描述了能流输入充足的情况下,当加热元件状态变化时,介质温度的变化趋势。图中加热元件工作状态为随机变量,Tmax和Tmin分别表示用户可接受的最高温度和最低温度。当加热元件正常工作时,加热功率大于散热功率,热容器中介质温度由初始温度逐步上升,当上升到可接受最高温度Tmax时,调整输入容量,使得加热功率等于散热功率,保证介质温度不再变化;当加热元件故障时,热容器不断与周围环境交换热量,介质温度逐步降低,直到加热元件再次正常工作,介质温度才会上升。分别基于元件状态和介质温度评估供热系统工作状态,如图2所示,图中阴影表示正常状态,空白表示故障状态。基于加热元件状态评估系统可靠性时,若加热元件故障,则判定系统故障;基于介质温度评估系统可靠性时,若加热元件故障,介质温度将逐步下降而非突变,只要温度处于用户可接受范围内,则判定系统正常。二者的区别在于加热元件状态为0-1变量,元件由正常变为故障时其状态会发生突变,而介质温度则是连续变量,不会发生突变。因此,基于介质温度的热网可靠性评估模型更为精确。
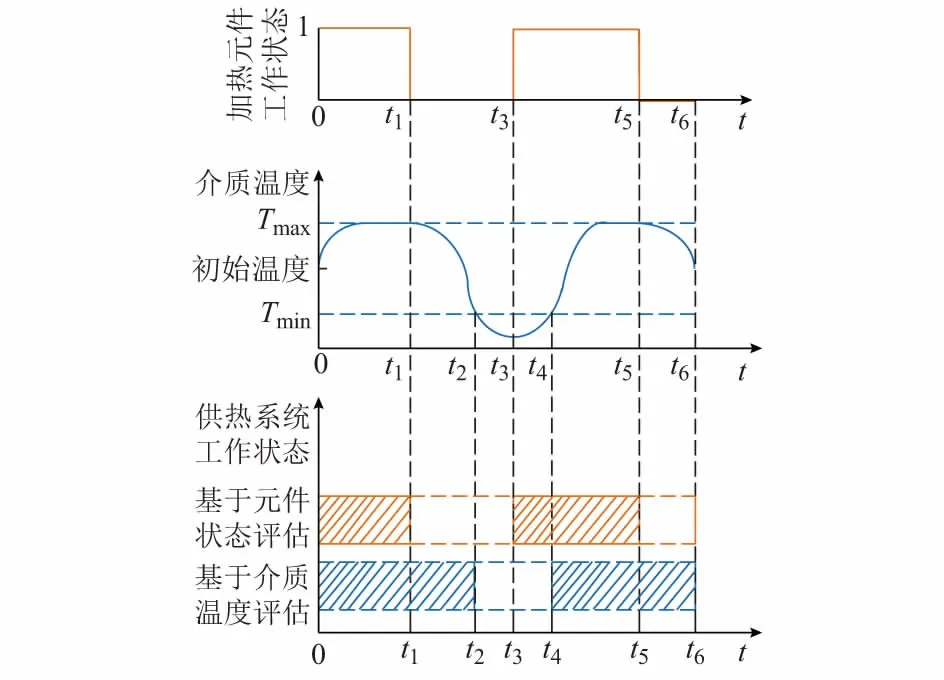
图2 热惯性示意图Fig.2 Diagram of thermal intertia
为了描述温度变化的惯性过程,采用线性能量平衡法[16-18],对热惯性过程进行建模。假设任意时刻热水罐内热水温度均匀且只有一个加热元件,则任意时刻的温度变化趋势为:
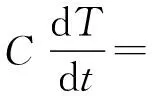
ceq(t)(Td-Tin)+Pth(t)
(5)
式中:C为热容量;R为容器热阻;T(t)和Ta(t)分别为t时刻热水温度和环境温度;ce为水的比热容;q(t)为t时刻用水速率;Td为热水期望温度;Tin为进入系统的冷水温度;Pth(t)为t时刻加热功率。
热平衡方程描述了热水温度与环境温度、加热功率间的惯性关系。为简化计算,可对热惯性模型进行准稳态处理。首先,将一个典型日平均分为D个时段,时段序号为i,则可根据各时段热负荷及其余参数计算每个时刻的热水使用量为:
(6)
式中:Pthe(i)为i时段的热负荷;kw为热水负荷比例系数。
假设各时段温度变化率恒定,则热水温度满足:
(7)
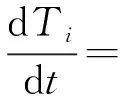
ceq(i)(Td-Tin)+Pactual(i)]
(8)
式中:Δt为各时段持续时间;Pactual(i)为i时段的实际加热功率。
3 IES基本运行策略
IES的运行策略涉及能流调度,其本质是一个寻优过程。在进行IES可靠性评估时,也应考虑其运行策略。根据各子系统能否独立满足用能需求,将IES工作状态划分为正常状态和危险状态。基于现有运行策略[10]和不同能源品味差异,本文设置IES基本运行策略如下。
1)同种能源之间相互供应的优先程度最高
能源的转换必然伴随着损耗和延迟,因此在能流输入能够满足负荷需求的情况下,优先使用同种能源。
2)依据能源品味等要素确定各子系统重要程度为电力>天然气>热
为实现IES中不同能流间的科学比较,采用分析法计算各子系统能流的值。是系统或物质流、能量流达到与参考环境平衡时所产生的最大功[19]。它反映了能量转换的不可逆损失和能量传递的方向性,揭示能量利用过程的本质,描述了能流“质”的差异。
在IES中,电能可将全部能量用于做功,因此电能值等于其能量值,即
ex,e=ee
(9)
式中:ex,e为电能值;ee为电能的比能量值。
天然气能量的本质是燃烧产生的化学,可通过系数[20-22]计算得到:
ex,c=ecσ
(10)
式中:ex,c为天然气值;ec为燃料的比能量值;σ为系数,常见能源的系数见附录A表A1。
热水计算方法为:
(11)
式中:ex,th为热水值;T0为基准温度;Th为热水温度;Δq为单位质量热水所含热量。
综上,电能、天然气相对热能,单位值更高,易于转化利用,应当具有较高的优先级。
对电能和天然气进行进一步的比较。从安全性、经济性、环保性、便捷性这4个一级指标和用能伤亡人数、故障率、修复率、单位能量购买成本、二氧化碳排放量、污染物排放量、供能半径、用能半径8个二级指标进行评估,其中修复率、供能半径、用能半径为正指标,其余为负指标,评价体系表如附录A表A2所示。对各指标赋分后可得电能和天然气对应的能源特征雷达图,如附录B图B1所示。经比较可知,电能的经济性稍差于天然气,但其安全性、环保性和便捷性更优,是更好的终端能源形式。因此,当系统处于危险状态时应优先保障电力子系统安全。
3)在正常状态下,各子系统的能流输入均能独立满足负荷需求,超出部分作为备用或支援容量
4)在危险状态下,能流输入不足的子系统接受其他子系统的支援以满足负荷需求,支援容量受设备转换容量和工作状态限制
5)连续稳定的运行方式不是保证热能供应的唯一方式。根据式(5)至式(8)可计算得出某一确定流量和热水期望温度所对应的最小加热功率,从而可计算得出热力子系统可停供容量基于上述运行策略的供能流程图如图3所示。
4 计及热惯性和运行策略的IES可靠性评估
4.1 IES状态空间图
在两状态模型下,n个元件将产生2n个状态。假设同一时刻最多只有一个元件的状态发生变化,根据各元件的故障率和修复率参数,可建立IES状态空间图及状态转移矩阵。
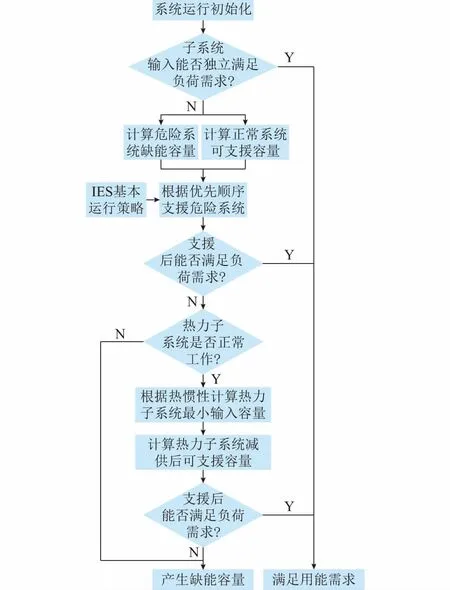
图3 基于基本运行策略的供能流程图Fig.3 Flow chart of energy supply based on basic operation strategy
若当前系统状态为i,则在t时刻,从状态i到状态j的转移满足如下分布:
fsi→sj(t)=λije-λijt
(12)
式中:λij为从状态i到状态j的转移率。
当时间间隔很短时,转移概率可以近似计算为:
Psi→sj(Δt)≈λijΔt
(13)
(14)
式中:N为状态数,满足N=2n。
转移概率矩阵为:
(15)
累计转移概率为:
(16)
4.2 可靠性模型求解方法
采用基于马尔可夫链的蒙特卡洛方法对计及热惯性和运行策略的IES进行可靠性评估,总体思想是:首先模拟较长一段时间内系统状态的变化得到系统状态的样本,然后通过故障模式影响分析遍历各时间断面元件运行情况对系统负荷的影响,从而评估系统的可靠性指标。具体步骤如下。
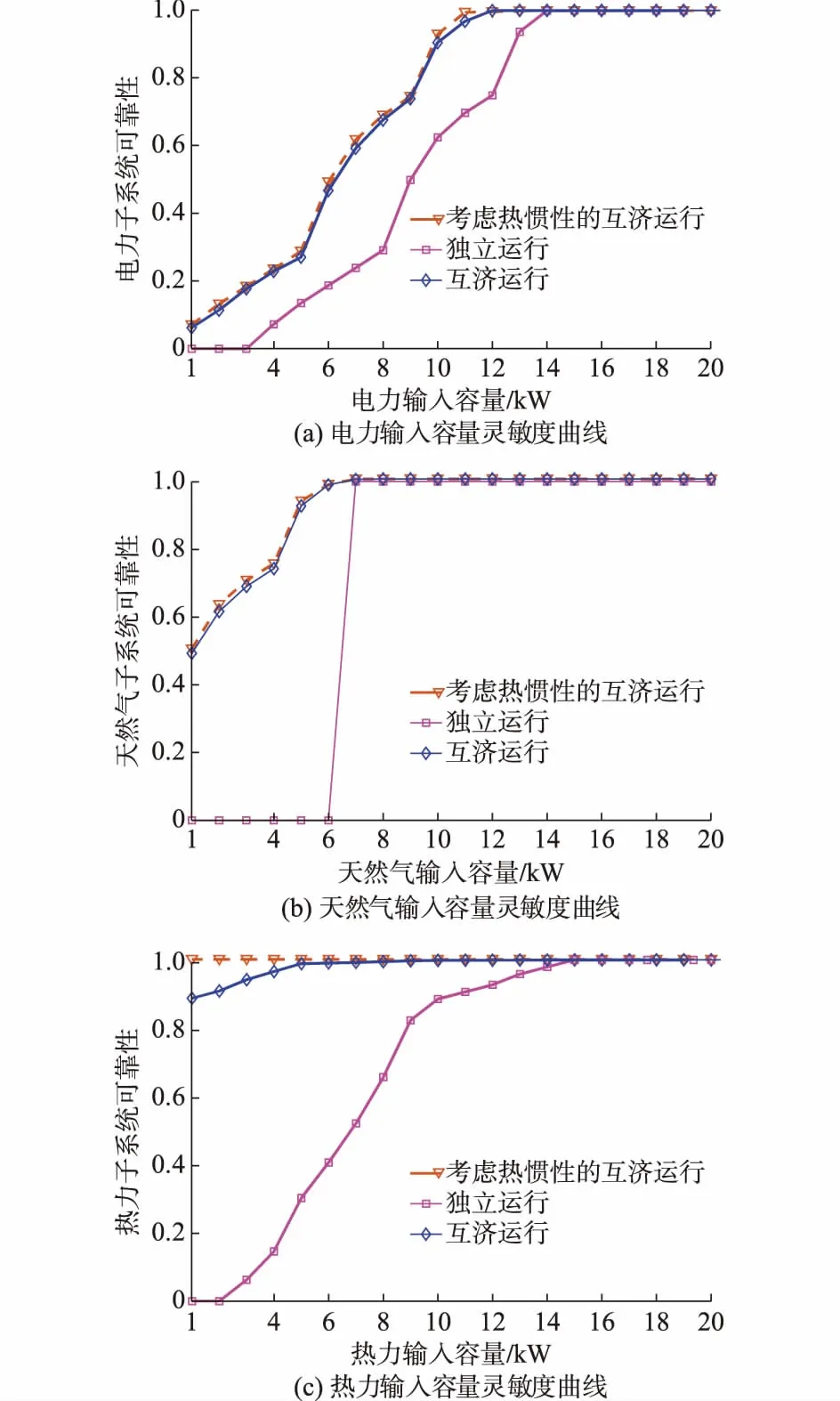
步骤1:建立马尔可夫状态空间。
步骤2:计算状态转移概率Psi→sj和转移累计概率Psum,ij。
步骤3:生成马尔可夫链,设置马尔可夫链初始状态,产生满足[0,1]均匀分布的随机数r并与累计概率相比较。若满足Psum,i,j-1 步骤4:判断新状态下工作模式。 步骤5:设置初始温度,计算新状态下每个时间断面内保持温度不低于Tmin的热功率。 步骤6:计算各能源转换设备出力和各子系统可获得的支援容量ξsup,α,模拟热负荷的温度变化情况。 步骤7:重复步骤3至步骤6,计算得到IES的可靠性。 为验证本文所提方法的有效性,本节对文献[15]中德国某用户级IES进行仿真分析。该用户级IES系统包括电力、天然气和热力子系统,其物理结构与设备构成如图4所示。图中,P2G表示可再生能源发电技术。 图4 用户级IES结构图Fig.4 Structure of user-level in IES 在能源供给方面,由上级供能网络为用户供能, 电能输入为26 kW,天然气输入为8 kW。当各子系统独立运行时,电力和天然气子系统分别通过变压器和天然气管道直接供能,热力子系统则由电锅炉供能,且上级配电网输入容量将平均分配给电力子系统和热力子系统。 在能源转换方面,当互济运行时,各能源转换设备都可参与供能,能源转换设备参数包括能源转换设备最大容量矩阵ξmax;故障率矩阵W;修复率矩阵F;具体参数如下: (17) (18) (19) 式中:下标e,c,t分别表示电力子系统、天然气子系统、热力子系统;λij和μij分别表示将能流i转换为j的能源转换设备的故障率和修复率,其中i,j∈{e,c,t}。 在负荷需求方面,共有电、热、气三类负荷,其中电负荷和热负荷随时间变化较大,典型日负荷曲线如附录B图B2所示。热负荷共包括10个规格相同的热容器,总容量为1 m3,罐壁热导为0.903 5 J/(s·℃),正常运行时的温度范围为55~75 ℃。典型日各时刻环境温度见附录B图B3所示。 取热水期望温度和热容器中热水初始温度为65 ℃,可接受最低温度为55 ℃。基于蒙特卡洛方法对能流互济前后各子系统可靠性指标进行计算,模拟次数为100 000次,结果如表1所示。 表1 IES可靠性指标Table 1 Reliability indices of IES 由表1可知,当各子系统独立运行时,可靠性取决于输入能流与负荷需求的大小关系和设备可用度。算例中天然气输入能够支持典型日96个时刻用能需求,电力和热力输入分别能够支持93个时刻和92个时刻的用能需求,因此天然气子系统可靠性略高于电力和热力子系统。在考虑热惯性后,电力和天然气子系统独立运行的可靠性保持不变,热力子系统独立运行的可靠性上升为99.925 1%。这是由于热力子系统的用能本质是获得可接受的温度,当能流输入不足或加热元件故障时,热水温度将缓慢下降而不是突变,在一段时间内仍然能够满足用户需求。经计算可知,在用水量为0.002 L/s、加热功率为0的情况下,热容器中热水温度平均每小时下降4.5 ℃,在温度降低到55 ℃之前,热力子系统仍表现为正常状态,即当加热元件故障时,仍然能够继续使用133 min,因此现有的可靠性评估方法较为保守。同时,当热容器参数发生变化,现有方法的评估结果并不能体现参数变化后实际热量交换过程。 当互济运行时,在输入相同的情况下,电力、天然气和热力子系统的停供时间相比独立运行时分别减少为原来的3%,10%和2%,说明互济运行将带来较为明显的可靠性增益,尤其是能流输入不足的子系统其供能可靠性有较大提升。在考虑热惯性和多能互济的运行策略后,热力子系统可靠性接近于1,各子系统的可靠性进一步提升,这是由于考虑热惯性后,热力子系统能够在不影响自身可靠性的基础上减供或停供以支援危险系统,其可支援容量进一步提升,等价于系统备用容量的提升。 为探究热力子系统的热惯性行为,保持加热功率不变,取可接受最低温度比期望温度低5 ℃,计算不同热水期望温度和罐壁热导对应的热力子系统可靠性,如图5所示。 图5 热力子系统可靠性Fig.5 Reliability of thermal sub-system 由图5可知,罐壁热导越大、热水期望温度越高,热力子系统可靠性越低。当罐壁热导较小且期望温度较低时,此时热容器保温性能好,输入功率主要用来加热补充进入容器的冷水,加热后能够达到最低期望温度,可靠性较高。若不断提高期望温度,即使在热量损失较小的情况下,输入功率仍不足以将水加热到最低期望温度,因此可靠性反而降低。当罐壁热导为0、期望温度为77 ℃时,可靠性将降低到0。若不断增大罐壁热导,热容器散热功率逐步增大,输入功率中用于加热冷水的比重不断降低,即使在期望温度较低的情况下,可靠性也较低。当罐壁热导为3.6 J/(s·℃)、期望温度为60 ℃时,可靠性将降低到0。 为探究支援设备的故障率对电力子系统停供时间的灵敏度,分别计算支援设备不同故障率下电力子系统的停供时间增益,电转热装置通过备用容量和可减供容量支援,气转电装置通过备用容量支援,计算结果如图6所示。 图6 支援设备故障率灵敏度曲线Fig.6 Sensitivity curves of failure rate for support devices 由图6可知,随着故障率的变化,电转热装置对停供时间增益的影响明显大于气转电装置,这是由可支援容量与负荷需求之间的大小关系决定的。结合典型日负荷曲线可知,当电力子系统输入为0时,电转热装置的支援容量能够满足全部时刻的负荷需求,而气转电装置不能独立支持负荷。同时,即使电转热装置的故障率上升到52次/a,即一周故障一次,系统仍能获得约12 830 min的停供时间增益,再次说明了能流互济的可靠性增益。 为探究输入容量与可靠性的关系,分别计算不同输入容量下各子系统的可靠性指标,结果如图7所示。由图7可知,从运行模式来看,互济运行的可靠性始终高于独立运行的可靠性,且不考虑热惯性的可靠性评估结果略为保守。从输入容量来看,当各子系统输入容量小于最小负荷需求,独立运行可靠性均为0,而互济运行时,其他子系统的支援使得各子系统仍具有一定可靠性。随着输入容量不断增大,各子系统可靠性不断提升,但独立运行时与互济运行时的可靠性差异较大。当输入容量大于最大负荷需求,各子系统可靠性均提升至99.9%以上,此时增加单位容量能流输入所对应的可靠性增益逐步递减,且独立运行和互济运行的可靠性差别较小。进一步分析电力子系统可知,当电力输入为13 kW且独立运行时,供电可靠性为96.742 4%,当互济运行时,仅需要11 kW左右的电能输入就能达到这一可靠性水平,相当于节约了15%的容量,说明能流互济的运行机制不仅能够提升可靠性,也具有潜在的经济效益。 图7 各子系统输入容量灵敏度曲线Fig.7 Sensitivity curves of input capacity for different systems 本文计及IES多时间尺度,考虑热力子系统的热惯性和多能互济的基本运行策略,提出IES可靠性评估方法。通过对比各子系统独立运行和考虑热惯性及运行策略的互济运行,得出以下结论。 1)IES的多能互济机制能够有效提升各子系统的可靠性,尤其是当子系统能流输入不足时,受援后可靠性增益明显。但可靠性增益与负荷需求、最大支援容量有关。 2)当前不考虑能源时间尺度差异性的可靠性评估方法较为保守,尤其是对热惯性较大的子系统,持续供能并不是满足供能质量的唯一方式,个别元件故障并不影响系统的正常工作,因此需要从用户体验角度进行热力子系统的可靠性评估。 3)在考虑热惯性的基础上,根据能流特征制定合理的IES运行策略能够进一步增强系统的可靠性,一定程度上延缓了IES投资,具有较大的潜在经济效益。 在未来的研究中,将根据不同能流的时间尺度差异进一步精细化建模,刻画故障后IES中各子系统的动态变化过程,研究不同能源输入和不同运行策略对IES可靠性的影响,从而进一步完善综合能源系统的可靠性评估方法。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。5 算例分析
5.1 算例说明
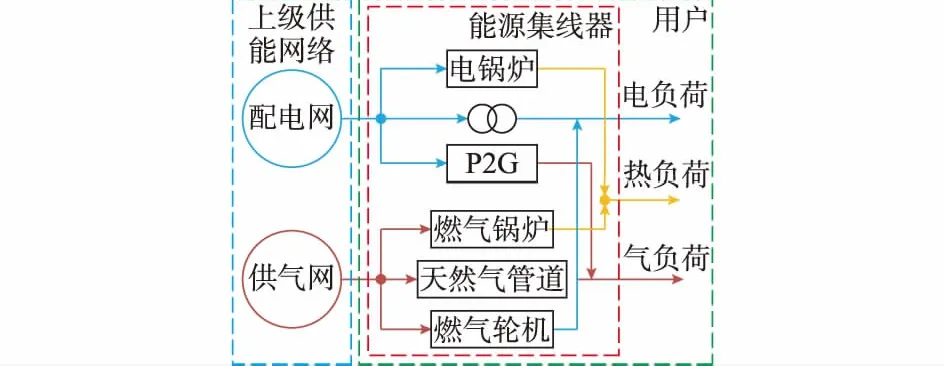
5.2 结果分析

6 结语

