含单相配电支路的配电网单相接地故障行波测距技术
齐 郑, 杭天琦, 林健雄, 薛 融
(1. 华北电力大学电气与电子工程学院, 北京市 102206; 2. 广州供电局有限公司, 广东省广州市 510620)
0 引言
中国配电网多为中性点非有效接地系统,单相接地故障约占所有故障的80%[1]。准确定位单相接地故障点是一直以来研究的热点。行波法作为一种行之有效的方法,已经逐渐运用在配电网中[2-3]。
行波法从原理上可以分为单端法和双端法[4-7]。由于配电网分支众多,使用双端行波测距成本较高,工程上难以实现全网覆盖, 因此学者们对单端行波测距进行了深入分析。传统单端法是利用故障初始行波首波头到达时刻和对端母线或者故障点反射波到达时刻的时间差进行定位。然而配电网折反射现象较多,反射行波的识别困难,电压互感器传变特性不高,导致单端行波测距精度不高。文献[8]采用基于零模—线模时间差的测距方法,利用不同模分量波速不同导致到达时刻不同,得到故障距离。该方法实现了单端定位,且不需要进行时间同步,实现简单,因此得到了较为广泛的应用。
当前很多供电公司基于节约成本的考虑,在很多部分配电采用单相配电的方式[9]。具体实现方式为:10 kV中压三相配电线路在某个位置(电杆或电缆分支箱)只引出两相线路到末端负荷,通过单相配电变压器(10 kV /220 V)连接负荷。单相配电方式能够降低线路成本,并在一定程度上提高供电可靠性及降低线损。含单相配电支路的配电网在发生单相接地故障后,行波传输过程相对复杂,影响了基于行波的故障测距准确性。当前针对含单相配电支路的单相接地故障测距技术研究较少,研究适应单相配电支路的测距方法具有积极意义。
本文研究了线路末端含有单相配电支路的辐射状配电网发生单相接地故障后的故障测距技术,包含了行波传输机理分析,以及根据线模、零模分量传输时间差进行故障测距的实现方案。利用EMTP/ATP仿真软件验证了本文提出方法的可靠性和准确性。
1 含单相配电支路的配电网行波传输机理分析
1.1 相模变换研究
当故障发生后,其暂态电压行波的波传输过程可以用二阶偏微分方程表示:
(1)
式中:U为n根导线对地电压的列向量;x为输电线路的长度;L和C分别为线路上单位长度的电感和电容参数矩阵;t为时间。
由于线路中存在的耦合现象,L和C都是n阶满阵,其乘积不是对角阵。分析行波传输过程时,需要采用适当的矩阵变换,将LC转换为对角阵。以电压行波为例,采用Karenbauer变换矩阵S进行相似变换[10],得到
S-1LCS=Λu
(2)
式中:Λu为矩阵变换后的模量对角阵;S-1为Karenbauer逆变换矩阵。
对于n相输电线路,变换矩阵为:

(3)
将式(2)代入式(1)中,可以得到变换后模电压方程为:
(4)
Um为模量上的电压向量,进一步得到:
Um=S-1U
(5)
因此,单相配电支路和三相配电支路的Karenbauer变换形式分别为:
(6)
(7)
式中:ua,ub,uc分别为三相电压;um0(3),um1(3),um2(3)为线模分量;um0(2)和um1(2)为零模分量。
1.2 模量波速研究
假设线路电感参数矩阵的对角元素为Lk,非对角元素为Lok,电容参数矩阵的对角元素为Ck,非对角元素为Cok,根据文献[10]可得到三相配电支路线模分量和零模分量的波速为:
(8)
式中:vm1(3)和vm2(3)为三相配电支路的线模分量波速;vm0(3)为三相配电支路的零模分量波速。
同理,可以得到单相配电支路线模分量和零模分量的波速为:
(9)
式中:vm1(2)和vm0(2)分别为单相配电支路线模分量和零模分量的波速。由于配电网线路较短,零模分量的色散现象不严重,本文假定零模分量的速度仅由线路参数决定[11]。分析式(8)和式(9)可以看出,单相配电支路和三相配电支路的线模分量波速相等,但是零模分量波速差别较大。
1.3 单相接地故障行波传输过程分析
1.3.1故障发生在单相配电支路的传输过程
如图1所示为一个含有单相配电支路配电网示意图,其中三相配电支路供电相A,B相与单相配电支路相连。P点为检测装置所在位置,K点为三相配电支路和单相配电支路的分界处,单相配电支路末端为配电变压器。假设单相配电支路发生A相接地故障,故障点与检测装置的距离为lf,l1为分界点到检测装置的距离。
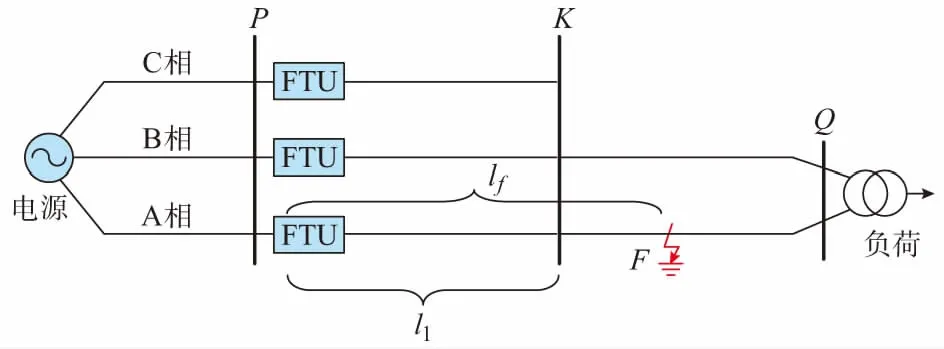
图1 含有单相配电支路配电网模型Fig.1 Distribution network model with single-phase power supply line
根据叠加定理,故障后的等值电路可以等效为故障前正常的网络以及故障后的附加电源作用的网络之和[12]。故障暂态行波为附加电源作用在线路故障点处产生的行波。
采用式(6)所述的相模变换后,得到电压行波的线模分量和零模分量。二者到达分界处K后,可以通过Karenbauer反变换得到相电压:
(10)
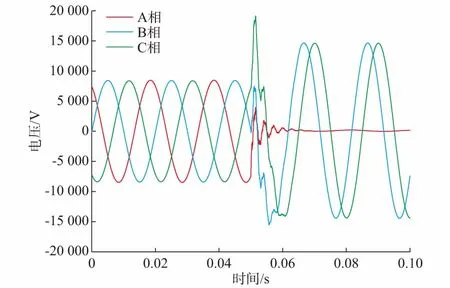
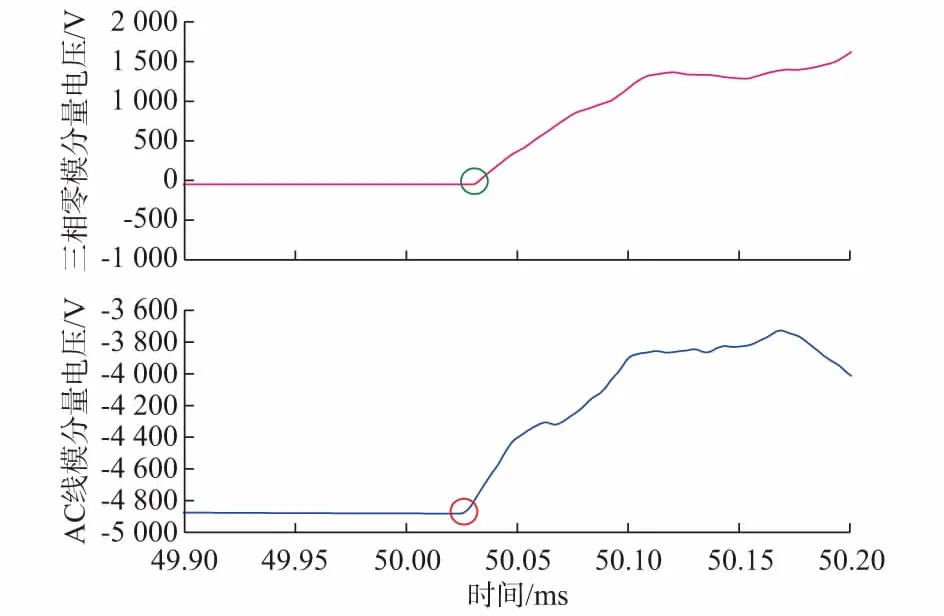
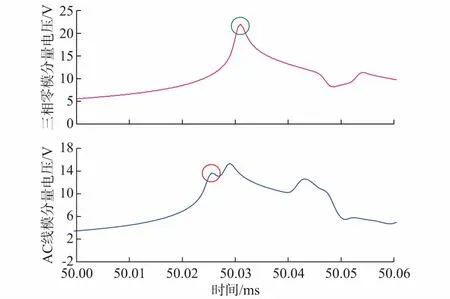
假设三相配电支路的参数对称,且存在耦合系数k(0 uc=kua+kub (11) 由式(7)可以计算出三相配电支路的线模分量和零模分量为: (12) 由式(12)可以看出线模分量和零模分量将继续沿着三相配电支路传输线模分量到达P的时间tP1为: (13) 而零模分量到达P的时间tP0为: (14) 综上所述,行波从单相配电支路传输到三相配电支路的过程比较复杂,行波线模分量和零模分量初始波头到达P点的时刻与行波在单相配电支路及三相配电支路上的传输过程相关。 1.3.2故障发生在三相配电支路的传输过程 故障发生在三相配电支路分为两种情况。第一种情况,如果在三相配电支路的A相或者B相发生单相接地故障,如图2中的F1点所示,其中l2为分界点到线路末端变压器的距离。 图2 三相配电支路上发生单相接地故障的模型Fig.2 Model of single phase-to-ground fault at three-phase supply line 采用式(7)所述的相模变换后,得到三相电压行波的线模分量和零模分量。线模分量和零模分量向两侧传输,向负荷侧传输的行波到达分界处K后,可以通过Karenbauer反变换得到相电压: (15) 因此单相配电支路的线模分量和零模分量可以根据式(6)和式(15)得到: (16) 可以看出线模分量和零模分量将继续沿着单相配电支路继续传输。 同时,向检测点P传输的线模分量到达P点的时间为: (17) 向检测点P传输的零模分量到达P点的时间为: (18) 第二种情况,如果在三相配电支路的C相发生单相接地故障,如图2中的F2所示。根据同样的方法分析故障行波从三相配电支路向单相配电支路的传输过程。然而,由于C相线路与A相或B相的耦合情况是相同的,所以在单相配电支路中AB两相线模分量为: (19) 因此当三相配电支路发生C相接地故障时,只有零模分量经过分界点从三相配电支路传输到了单相配电支路。 同理线模分量和零模分量到达P点时间为tP1和tP0,有 (20) 综上所述,行波从三相配电支路传输到单相配电支路的过程比较复杂,但是无论在三相配电支路的A相、B相或者C相发生单相接地故障,行波线模分量和零模分量初始波头到达P点的时刻只和行波在三相配电支路上的传输过程有关,不受行波越过分界点在单相配电支路上的传输过程的影响。 由于通常单相配电支路上很少安装电压互感器、馈线终端设备(FTU)等检测装置,因此本文研究利用三相线路上的检测装置进行故障定位,如图1中的P点。目前FTU的采样率还不足以测量行波信号,可以采用专门的高频采样设备与FTU并联,测量电压行波信号。未来随着电子产品价格下降,完全可以实现FTU带有行波检测功能。 要实现全网的准确定位、排除伪故障点,需首先缩小故障范围,本文借助当前较为成熟的配电网区段定位技术,确定故障点所在的区段[14-15]。当故障区段含有单相配电支路时,需要在故障区段内判定故障点位于三相配电支路还是单相配电支路。 仍以文中图1所示系统为例,假设故障发生在分界处K,检测装置获得的线模分量和零模分量到达的时间差为Δtcritical,可以计算出: (21) 因此,当实际的时间差Δt>Δtcritical时,说明故障点位于单相配电支路上;当实际的时间差Δt<Δtcritical时,说明故障点位于三相配电支路上。 如果故障点位于单相配电支路上,根据1.3.1节的分析结果,测距算法必须要全面考虑故障行波在单相配电支路和三相配电支路上的传输过程。设位于P点的检测装置检测到线模分量和零模分量到达的时间差为Δt=tP0-tP1,则根据式(13)和式(14)可以计算出故障距离为: (22) 如果故障点位于三相配电支路上,根据1.3.2节的分析结果,测距算法无需考虑故障行波越过分界点在单相配电支路上的传输过程。设位于P点的检测装置检测到线模分量和零模分量到达的时间差为Δt=tP0-tP1,则根据式(17)和式(18)可以计算出故障距离为: (23) 故障测距的流程如下。 1)位于三相配电支路上的检测装置实时测量电压电流等数据,当发生单相接地故障后利用区段定位技术判断故障点位于某检测装置下游[14-15]。 2)检测装置截取故障前后一段时间内的三相电压信号,利用Karenbauer变换得到电压行波的线模和零模分量。 3)利用希尔伯特—黄变换(HHT)[16-17]作为波头提取的方法,获得电压行波线模分量和零模分量的波头到达时刻,进而求出线模分量和零模分量的到达时间差Δt。 4)判断故障点所在三相配电支路或是单相支路。利用网络结构计算出Δtcritical,当实际的时间差Δt>Δtcritical时,说明故障点位于单相配电支路上,否则说明故障点位于三相配电支路上。 5)如果故障点位于单相配电支路上,则利用式(22)计算出故障距离;如果故障点位于三相配电支路上,则利用式(23)计算出故障距离。 本文所述定位技术已在工程现场应用,检测装置的采样频率为2 MHz。本文通过EMTP/ATP仿真软件搭建了与实际配电网匹配的模型进行仿真,如附录A图A1所示。线路P-K-Q段为故障线路,三相配电支路通过A,B相延长到单相配电支路,假设检测装置位于P点,P点下游的三相配电支路长度为5 km。 模型中导线型号为LGJ-120,可得三相配电支路和单相配电支路电感和电容参数如附录B表B1所示。 附录B表B1中,L1和L0分别为单位长度的线路线模电感和零模电感,C1和C0分别为单位长度的线模电容和零模电容。由表B1的线路参数可以计算得到三相配电支路和单相配电支路电压行波线模波速为:vm1(3)=vm1(2)=2.975 2×105km/s;三相配电支路的电压行波零模波速为:vm0(3)=2.634 8×105km/s;单相配电支路的电压行波零模波速为:vm0(2)=2.171 8×105km/s。 通过线路长度和三相配电支路的电压行波线模分量和零模分量的波速,可以计算出分界点处发生单相接地故障时电压行波的线模、零模分量到达时间差Δtcritical=2.17 μs。本文通过如下不同案例对故障测距方法进行测试。 单相接地故障发生在单相配电支路上,过渡电阻为10 Ω,故障点距离分界K处 2.54 km,故障类型为A相接地故障。在检测装置P点处测量三相电压行波如图3所示。 图3 三相电压波形Fig.3 Three-phase voltage waveforms 计算AC相的线模分量和三相电压零模分量,结果如图4所示。可以明显看出电压行波线模和零模分量到达时刻存在时间差。对AC相线模分量和三相零模分量进行HHT,得到变换后的波形如图5所示。 图4 线模分量和零模分量波形Fig.4 Waveforms of aerial and zero mode component 由图5计算出电压行波线模分量和零模分量到达时间差为Δt=5.5 μs,可以发现Δt>Δtcritical,说明故障位于单相配电支路上。由式(22)可以计算出故障点与P点的距离lf为7.677 km,与实际故障距离7.54 km相比,相对误差为1.8%。可见测距在金属性接地故障中,多模量测距方法可以达到较高的精度。 图5 线模分量和零模分量的HHT结果Fig.5 HHT result of aerial-mode and zero-mode component 为了验证本文提出的多模量波速差测距算法的准确性,将传统三相电压行波零模-线模波速差方法作为对比,分别在单相配电支路设置不同故障点,得到对比结果如附录B表B2所示。 从附录B表B2的测距结果可以看出,当故障发生在单相配电支路上,传统三相电压行波线模-零模时间差测距方法会出现不同程度的误差,并且故障距离分界点越远,其误差越大。而本文提出的多模量波速差测距法,基本不受故障点位置影响,测距精度较高,能有效解决含有单相配电支路的单相接地故障测距问题。 为了进一步验证本文所提算法的适用性,模拟经高阻接地故障进行分析。单相接地故障发生在单相配电支路上,故障点距离分界K处2.54 km,故障类型为A相经3 kΩ电阻接地故障。 在检测装置P点处测量三相电压行波如附录A图A2所示,计算AC相的电压行波线模分量和三相电压零模分量,结果如附录A图A3所示。可以明显看出电压行波线模和零模分量到达时刻存在时间差。对AC相线模分量和三相零模分量进行HHT,得到变换后的波形如附录A图A4所示。 从图A4可以看出,虽然暂态行波受过渡电阻影响特征而削弱,但是经过HHT后首波头的突变点依然容易辨识。由图A4计算出电压行波线模分量和零模分量到达时间差为Δt=6 μs,可以发现Δt>Δtcritical,说明故障位于单相配电支路上。由式(22)可以计算出故障点与P点的距离lf为8.079 km,与实际故障距离7.54 km相比,相对误差为7.1%。可见测距误差会受到接地接地电阻值大小的影响,高阻接地的测量误差相对金属性接地误差稍大,但仍在可接受范围内。 行波测距的精度受故障点与检测装置位置的距离影响。附录B表B3为故障点到检测装置不同距离的仿真结果(接地电阻均为100 Ω)。从附录B表B3可以看出,故障发生在检测装置出口处时难以准确定位,测距存在死区,这是受采样率限制无法有效确定电压行波线模、零模波头到达时刻的缘故。 本文通过对线路末端含有单相配电支路的辐射状配电网发生单相接地故障后的行波传输特性进行分析,揭示了三相配电线路与单相配电线路在相模变换中的差异。本文提出了基于多模量波速差的故障支路判断及故障测距方法,对基于零模-线模分量波速差的定位方法进行了较好的补充和完善。通过ATP仿真表明,本文提出的方法能够有效解决线路末端含有单相配电支路的辐射状配电网单相接地故障定位问题,受过渡电阻的影响较小。 本文基于常规辐射状配电网进行分析,随着环网结构增加及分布式电源更多接入[18-19],对本文提出的行波测距技术是一个挑战,将在以后的科研工作中进一步深入分析。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 (编辑代长振)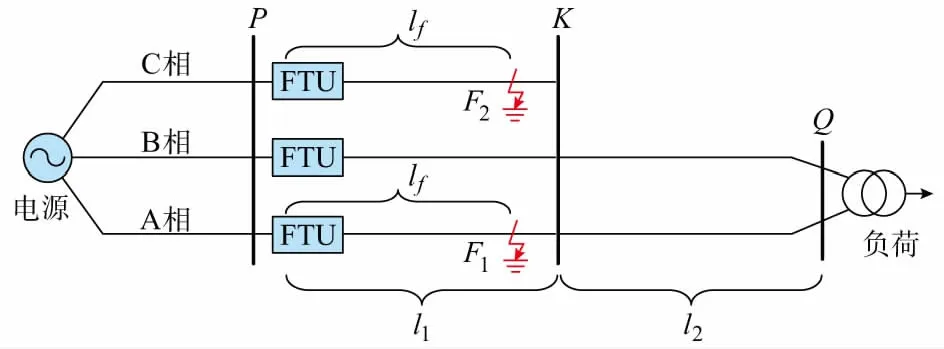
2 基于多模量波速差的行波测距
2.1 故障支路判定
2.2 故障距离计算
2.3 算法流程
3 仿真分析
3.1 经低过渡电阻接地
3.2 经高过渡电阻接地
3.3 故障点与检测装置的距离影响
4 结语

