多区域并行协同的多目标分布式帕累托最优潮流算法

郑宝敏, 余 涛, 瞿凯平, 张孝顺, 殷林飞

(1. 华南理工大学电力学院, 广东省广州市 510640; 2. 广东省绿色能源技术重点实验室(华南理工大学), 广东省广州市 510640)

0 引言

目前,求解帕累托多目标优化问题的方法主要包括智能化搜索方法和传统优化方法。智能化搜索方法本质上是一种随机搜索方法,如带精英策略的非支配解排序遗传算法(elitist non-dominated sorting genetic algorithm,NSGA-Ⅱ)[1-2]、多目标进化算法[3-4]、多目标粒子群算法[5-6]等,这些方法通过一定策略不断搜索并更新帕累托最优解集。然而,当问题规模较大时由于搜索的空间过大会导致求解时间大大增加。传统优化方法,如ε约束法[7]、法线边界交叉(normal boundary intersection,NBI)[8-9]法、规格化平面约束(normalized normal constraint,NNC)[10]法等,通过数学上的约束可将多目标优化问题转换为一系列单目标优化问题,并通过求解所有单目标优化问题得到帕累托最优解集。该类方法由于计算速度快,可适用于求解电网的大规模优化问题。然而,这类方法大部分属于集中式的求解方法,对于多区域互联大电网,容易出现以下问题。

1)集中优化器需采集整个系统信息进行优化决策,容易导致通信和信息处理瓶颈。

2)随着电网规模的增大,优化问题的求解规模和复杂度也随之增加,优化问题的求解精度下降,计算时间过长。

3)由于采用集中式调控的框架,因此运行设备信息的高私密性以及系统运行的高可靠性就无法得到满足。尤其是在开放电力市场的形势下,计算过程中的信息保密问题就显得愈发重要。

针对上述问题,寻求一种高私密性的分布式帕累托多目标优化方法显得尤为重要。近年来,大规模复杂电网的分解协调计算和分布式优化方法已经在最优潮流[11-12]、无功优化[13-14]、经济调度[15-16]和风险调度[17]等领域得到广泛应用。其中,文献[11]基于电网分区的分布式计算环境,提出了同步迭代、异步迭代和实时跟踪等值等几种分解协调的计算模式。文献[12]搭建了统一仿真平台,比较了7种最优潮流分解协调算法的收敛性、计算速度和通信量等计算性能,并分析了参数变化对算法稳定性的影响。这些方法有效降低了优化问题的求解规模,实现了优化问题的分布式求解计算。同时,与集中式方法的全局信息采集方式不同,这些方法在优化过程中只须交换边界信息。然而,绝大部分研究只涉及单目标的分布式优化,或只是将多目标问题通过简单线性加权转换为单目标问题[14],未能真正实现分布式的帕累托多目标优化求解。

基于此,本文提出了一种基于NBI法的多区域并行协同的多目标分布式帕累托优化算法。该算法克服了传统集中式优化方法的缺点,实现了去中心化的多目标分布式并行优化计算。

1 多目标分布式帕累托最优潮流模型

1.1 分布式优化框架

搭建的分布式优化框架如附录A图A1所示。首先,将多目标优化问题分解为与各区域对应的子优化问题。每个区域采用单独的优化器完成子问题的优化,且在优化过程中只须与互联区域交换少量的边界信息和虚拟目标因子信息,即可进行全局调整。完成原问题的优化后,各区域能量管理系统(energy management system,EMS)将控制指令下发到本区域。因此,与集中式优化框架相比,分布式优化框架下的设备私密性更高,系统运行可靠性更高,且可有效减少计算内存,并易于扩展计算。

1.2 数学模型

本文构建的最优潮流模型以最小化发电费用、碳排放和有功网损为优化目标,同时满足潮流、发电机组出力、节点电压以及线路容量上、下限等约束条件,如下所示。

(1)

(2)

式中:NG,ND,NB,NL分别为发电机组、负荷、节点和支路集合;ai,bi,ci为第i台发电机组的费用系数;αi,βi,δi为第i台发电机组的碳排放系数;PGi和QGi分别为节点i的有功注入功率和无功注入功率;PDj和QDj分别为节点i的有功负荷和无功负荷;gij,bij,θij分别为节点i与j之间的电导、电纳和角度;Vi为节点i的电压幅值;Pl为支路l流过的有功功率;PGi,max和PGi,min,QGi,max和QGi,min,Vi,max和Vi,min,Pl,max和Pl,min分别为发电机组有功出力和无功出力、节点电压以及支路容量上限、下限;x为所有决策变量构成的向量。

2 分布式帕累托多目标优化

2.1 NBI法的基本原理

采用NBI法求解式(1)和式(2)构成的多目标优化问题[8]。为叙述简便,将式(1)和式(2)写成如下紧凑形式。

min (f1(x),f2(x),f3(x))

(3)

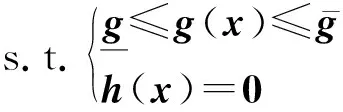
(4)

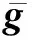
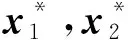
(5)

(6)

(7)

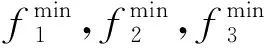
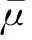
min(-Dt)

(8)

(9)

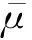
它把多目标优化问题转化为m个单目标优化问题,具体如下式所示:

(10)

式中:n为乌托邦平面的单位法向量;Zt为乌托邦平面点Zt的坐标向量。

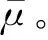
2.2 多区域协同分布式计算

采用节点撕裂法[12]实现多区域协同分布式计算。通过节点撕裂,将区域联络线中点一分为二并作为各区域的边界节点。如图1所示,将撕裂后的边界节点作为虚拟的发电机组节点,从而实现各区域的潮流平衡,使原系统分解为多个子区域,通过子区域的协同计算实现原系统问题的优化。图1中:PAB和QAB分别为区域A和B之间联络线的有功功率和无功功率;TAB和TBA分别为与区域B相联络的区域A的边界节点电气量和与区域A相联络的区域B的边界节点电气量;PA和QA以及PB和QB分别为区域A和区域B的有功注入功率和无功注入功率。

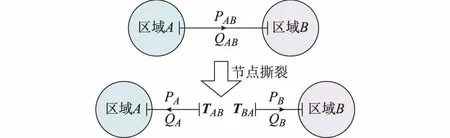
图1 多区域优化问题的分布式计算原理Fig.1 Distributed calculation principle for multi-area optimization problem

为不失一般性,在下文中均设原系统为n区域互联系统,且作出以下定义:NS为所有区域的集合;NB,i为与区域i互联的区域集合;NF,i为除去区域i后剩余区域的集合。

由于节点撕裂,互联区域之间的边界节点应在电气上等值,故对于互联的区域i和j(i∈NS,j∈NB,i),应满足式(11)所示的边界节点电气约束。规定边界节点的功率正方向为边界节点流向区域内部。

Hb,i(xb,i,xb,j)=ξijTij-ξjiTji=0

(11)

(12)

(13)

式中:Hb,i为区域i的边界节点电气约束;xb,i和xb,j分别为区域i和j的边界变量;Tij为与区域j相联络的区域i的边界节点电气变量,包括区域i的边界节点向区域i注入的有功功率Pij、无功功率Qij和边界节点的电压幅值Vij及相位θij;Tji为与区域i相联络的区域j的边界节点电气变量;ξij为区域i和j之间边界节点电气变量的方向修正因子,用于保证区域联络线上功率流向的一致性;I为单位矩阵。

2.3 多区域分布式多目标优化

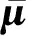
(14)

式中:n为子区域的个数;f1,i,f2,i,f3,i为子区域i的目标函数,称为目标因子。

在每个子区域i中,只存在本区域的目标因子f1,i,f2,i,f3,i,无法获知其他区域的目标因子,子区域无法表示原系统的目标值。故在每个子区域中,以区域i为例,引入虚拟目标因子以表示其他区域k(k∈NF,i)的实际目标因子,使区域i可以表示原系统的目标值,此时目标解表示如下:

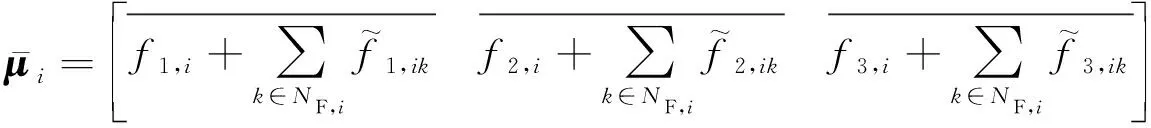
(15)

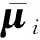
由式(15)知,此时区域i的目标解仅含本地变量,不存在其他区域的变量。由于区域i的虚拟目标因子是用于替换区域k的实际目标因子,故区域i应满足以下约束:

(16)

将式(16)写成隐式形式:

(17)

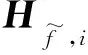
根据式(15)至式(17),优化问题(式(8)至式(10))可转换成用区域i表示的优化问题Fi,如式(18)和式(19)所示。

Fi=min(-Dt,i)

(18)

(19)

式中:Dt,i为由区域i表示的优化问题Fi中的垂直截距。

对于式(19),根据多区域分散计算的思想,可将约束条件中第一不等式约束直接分解为n个区域的不等式约束;根据式(11)至式(13),加入本区域i对外以及其他n-1个区域对外的边界节点电气约束,可将约束条件中第二式潮流约束分解为n个区域的等式潮流约束。故式(19)可拆分为式(20)和式(21)。

(20)

(21)

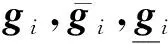
其中约束式(20)为区域i的本地约束;约束式(21)为其他n-1个区域须满足的约束。约束式(21)表明,在用区域i表示的原系统的优化问题中,还须保证其他区域满足原有的等式和不等式约束,才能实现与式(19)的等效。显然,根据式(18)、式(20)和式(21),任意区域i表示的优化问题Fi都可以与问题式(8)至式(10)等效。

不妨令Fi目标函数变为n(-Dt,i)。再将其改写成n个区域求和的形式,即式(22)。

(22)

为满足该等式,需保证区域i的Dt,i与其他所有区域k(k∈NF,i)的Dt,k相等。为实现上述条件,参照拆分约束条件式(19)的做法,需满足:

(23)

将式(23)与式(21)合并,得到与式(20)对称的其他n-1个区域的约束条件,再与式(20)可合并为n个区域的约束条件。

(24)

式中:∀i∈NS。

对于式(24)约束条件最后一式,每个区域均存在n-1个对外的虚拟目标因子约束,等式约束过于冗余,参照边界节点电气约束,每个区域只考虑与之联络区域的虚拟目标因子约束。故约束条件最后一式变为下式:

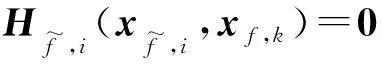
(25)

为简便起见,将式(24)约束条件中的边界节点电气约束和式(25)合并后归集为区域i对其他区域j的耦合约束,得到耦合等式约束,如式(26)和式(27)所示。

Hc,i(xc,i,xc,j)=0∀j∈NB,i

(26)

(27)

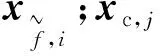
结合式(22)和式(24)至式(27),问题(式(8)至式(10))最终变为下式:

(28)

(29)

式中:∀i∈NS。

式(29)的约束条件包括n个区域的等式、不等式约束。分析知,只有最后一式才存在对外耦合关系,且最后一式表明,互联的区域之间通过耦合等式约束相互耦合,对其解耦,才能将分解为与n个区域对应的子优化问题,实现各区域的并行协同计算。

2.4 基于增广拉格朗日松弛和辅助问题原则法的并行协同计算

采用增广拉格朗日松弛(augmented Lagrange relaxation,ALR)法将式(29)中约束条件最后一式松弛到目标函数中,再采用辅助问题原则(auxiliary problem principle,APP)法将问题分解为n个子优化问题,由内点法求解n个子最小化问题,再通过并行迭代的方式实现原问题的协同优化[18]。

根据ALR法,将n个区域的耦合等式约束松弛到目标函数中,得到增广拉格朗日函数:

(30)

式中:λij为对应互联区域i和j之间耦合等式约束的拉格朗日乘子向量;cij为对应的二次耦合项系数。

在L中,对于每个区域i,因存在本区域与互联区域j的二次耦合项cij‖Gi(xc,i)-Gj(xc,j)‖2/2,L将难以分离,为此,参考文献[18]将L中的二次耦合项近似化:在耦合变量的当前第l次迭代处[xc,1,l,xc,2,l,,xc,n,l]线性化,再增加一个可分离的二次项。此时二次耦合项被解耦,其近似化表达式如式(31)所示。

cij,l(Gi(xc,i,l)-Gj(xc,j,l))TGi(xc,i)+

‖Gj(xc,j)-Gj(xc,j,l)‖2)

(31)

式中：bij,l为耦合系数。

此时,L可拆分为n个区域的本地变量表达式之和。由于剩余约束条件也为n个区域的本地变量约束,故原问题分解为n个子优化问题。根据APP法,此时,求解L的最小化问题变为并行迭代求解n个子最小化问题,每个最小化问题可通过内点法进行求解。根据APP法,每个区域i的第l+1步的迭代计算公式如式(32)和式(34)所示。当达到收敛条件时,迭代停止,原优化问题(式(8)至式(10))完成计算。对乌托邦平面上的所有均分点进行计算,最终得到帕累托前沿。

(32)

(33)

拉格朗日乘子第l+1步的迭代更新公式为:

(34)

2.5 算法步骤

根据ALR法和APP法,多目标优化问题变成n个区域的并行协同优化问题,求解流程如附录A图A3所示,具体求解步骤如下所示。

步骤1:系统分区。对联络线的中点进行节点撕裂,将原系统划分为n个区域。

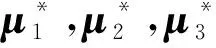
步骤3:设置乌托邦平面上均匀分布的点的个数m。即帕累托前沿由m个点构成,由于端点已计算,令t=4。

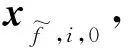
步骤5:各区域并行协同优化。根据λij,l,本区域i的xc,i,l以及与本区域相联络的所有区域j的xc,j,l,由式(32)并行求解n个子区域问题,得到每个区域第l+1步的运行点(xi,l+1,xc,i,l+1)。

步骤6:交换耦合变量数据。相互联络的区域i和j之间交换由边界变量和虚拟目标因子构成的耦合变量xc,i,l+1和xc,j,l+1。

步骤7:判断当前点的计算是否收敛,对所有区域依次进行收敛判断。若∀i∈NS且∀j∈NB,i,满足‖Hc,i(xc,i,xc,j)‖<ε,区域i计算收敛,令Eflag,i,l=1,否则令Eflag,i,l=0,将收敛标志发送至区域a,并等待区域A返回其他区域的收敛标志,待其他所有区域的收敛标志接收完成后,进行判断。若所有区域的收敛标志均为1,则停止当前点的计算,由步骤5得到的每个区域i的xi,l+1即为当前问题的最优解。令t=t+1,l=0,收敛标志全设置为0,跳转步骤9;否则,收敛标志全设置为0,跳转步骤8。

步骤8:更新拉格朗日乘子。根据式(34)求解计算λij,l+1。设置耦合系数bij,l+1和cij,l+1。令l=l+1,返回步骤5。

步骤9:判断帕累托前沿计算是否完成。若t≤m,返回步骤5,否则跳转步骤10。

步骤10:结束。计及步骤2中的3个端点,输出m个点的帕累托前沿。

3 仿真算例

为测试分区数量对算法性能的影响,参考文献[14]中的系统分区方式,选择合适的联络线节点,仿真算例将IEEE 118节点系统分别划分为二区域、三区域和四区域互联系统进行分布式多目标优化,并将计算结果与集中式NBI法进行对比验证了算法的可行性。系统分区情况如附录A图A4和表A1所示。发电机组的发电费用和碳排放参数见文献[19]。程序初始化设置如下:节点电压取值为0.94～1.06(标幺值),收敛精度为0.01(标幺值)[14],xc,i,0=0,λij,0=0,bij,l=2cij,l=1。硬件平台信息如下:CPU型号为Intel(R) Core(TM) i7-6700,主频3.4 GHz,内存为8 GB。程序开发环境为MATLAB R2016b 与GAMS 24.8,即用MATLAB编写分布式优化框架,用GAMS编写迭代过程中的内点法优化算法。

考虑发电费用和碳排放后,求解如附录A图A4中3种分区方式下两目标帕累托前沿,并采用最大满意度法[20]选出折中解。由单目标分布并行优化方法求出前沿上2个端点目标解μ1和μ2分别为[129 663.3,24 629.6]和[173 225.3,9 632.9]。在算例中,乌托邦线被划分为60段,即帕累托前沿共有61个点。分布式多目标算法与集中式NBI法的帕累托前沿对比如图2所示。

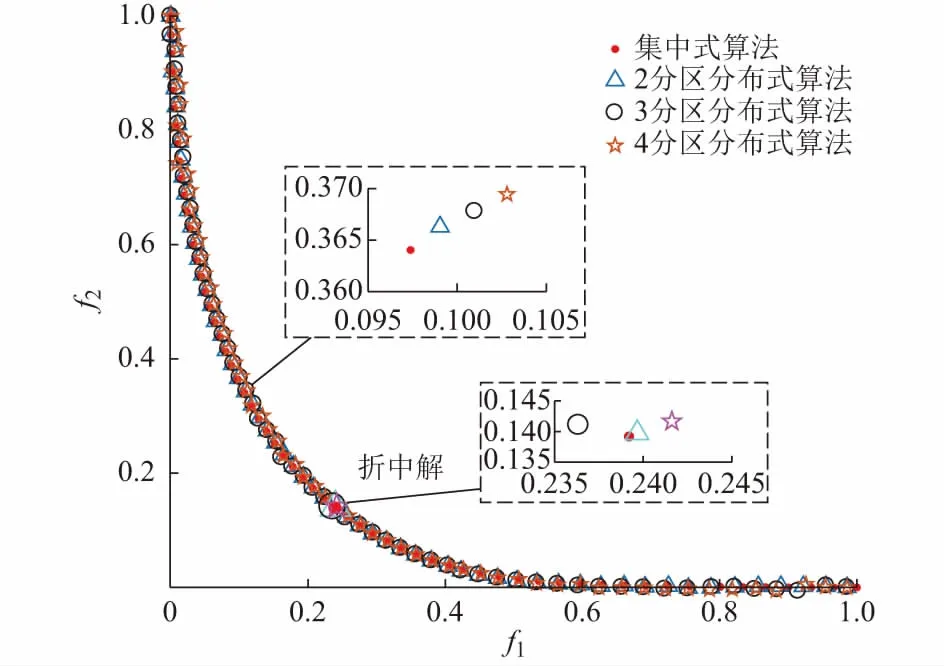
图2 多目标分布式优化算法(2个目标) 与集中式优化算法对比Fig.2 Comparison among multi-objective distributed optimization algorithm (2 objectives) and centralized optimization algorithm

考虑发电费用、碳排放量及有功网损这3个目标,求解在2分区方式下的3个目标帕累托前沿,并采用最大满意度法选出折中解。由单目标分布并行优化算法求出前沿上3个端点目标解μ1,μ2,μ3分别为[129 663.3,24 629.6,77.4],[173 225.3,9 632.9,49.0]和[166 388.6,122 34.9,9.2]。在算例中,乌托邦平面被136个点均分,即帕累托前沿共有136个点。分布式多目标优化算法与集中式NBI法的帕累托前沿对比如图3所示。各仿真算例下,折中解的具体结果对比如附录A表A2所示。由表中数据可知,分布式与集中式优化算法得到的折中解结果在一定的误差范围内保持一致。各仿真算例下,帕累托前沿上每个点的迭代步数如附录A图A5所示。

由图A5知,帕累托前沿上某些点的迭代步数会呈现跳跃式增长,对这些点的迭代数据分析发现,这是由于该点的初始值不好以及该点的耦合项系数cij,l取值过大导致收敛过程中总是跳过收敛点,导致收敛速度慢,但经过一定步数该点总能收敛。总体来说,在求解帕累托前沿的优化过程中,总收敛迭代步数较少,收敛速度快。

根据式(35)分析所提算法与集中式算法得到的帕累托前沿每个点的误差et:

(35)

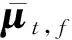
根据式(35),得到各仿真算例下帕累托前沿上每个点的误差结果如图4所示。

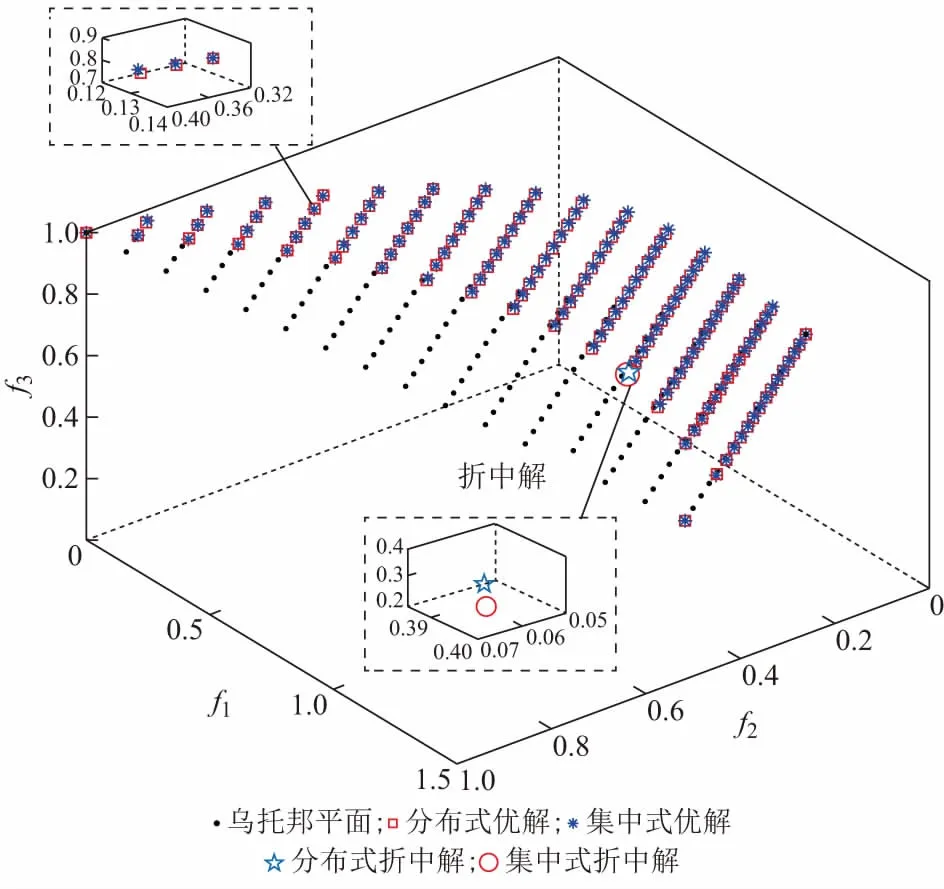
图3 多目标分布式优化算法(3个目标)与 集中式优化算法对比Fig.3 Comparison among multi-objective distributed optimization algorithm (3 objectives) and centralized optimization algorithm

由图4可知,在收敛精度为0.01(标幺值)的限制下,本文所提算法得到的帕累托前沿上每点误差最大不超过0.014(标幺值),误差基本保持在0.01(标幺值)以下,且该误差与收敛精度限制有关,会随着收敛精度限制的减小而减小。

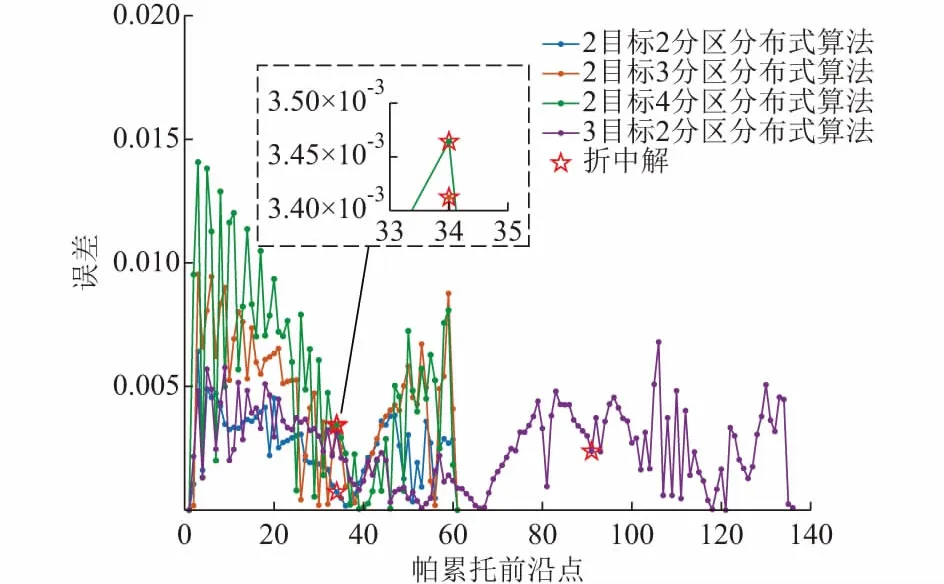
图4 分布式优化算法计算误差Fig.4 Calculation errors of distributed optimization algorithm

(36)

式中:m为帕累托前沿点的个数;Mt为计算帕累托前沿上第t个点所需的收敛步数。

单点平均计算时间为计算帕累托前沿一个点的所需的平均时间,等于帕累托前沿所有点的计算时间之和的平均值:

(37)

式中:τt为计算帕累托前沿上第t点所需的时间。

忽略通信时间,且由于n个区域并行迭代计算,故只考虑每次迭代过程的最大的区域计算时间。

(38)

式中:Tt,i,l为区域i在计算帕累托前沿上的第t个点时、第l步迭代计算所用的时间；Lt为第t个时点时迭代总步数。

根据下式分析本论文所提算法的效果与集中式算法的平均误差e为:

(39)

根据以上定义,采用多区域并行协同的多目标优化的计算结果与集中式优化结果对比如表1所示。

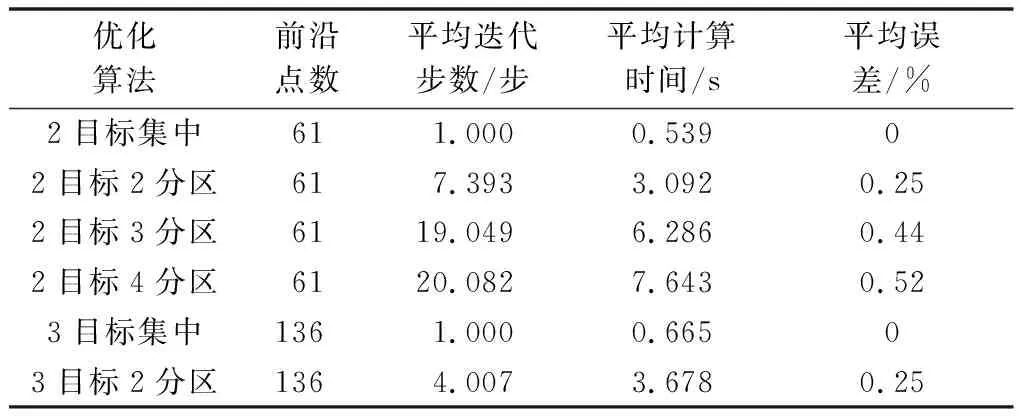
表1 多目标优化算法计算结果Table 1 Calculation results of multi-objective optimization algorithm

对表1数据进行分析得到以下结论。

1)在收敛精度为0.01(标幺值)的限制下,所提出的多区域并行协同分布式多目标优化算法与传统集中式算法优化效果趋于一致,帕累托单点平均误差不超过0.6%,若减小收敛精度,平均误差会进一步减小。三种分区方式下的计算结果验证了算法的准确性与有效性。

2)在计算时间上,所提算法与集中式算法相比,前者比后者稍慢,但前者整体计算速度仍在可接受的范围内。所提算法虽牺牲了一定的快速性但换取了计算的分布并行性,实现了分布并行的计算模式,减小了计算内存,提高了信息安全性。

3)算法的迭代步数及计算时间和分区情况有关。随着分区数目的增多,边界变量和虚拟目标因子变量的增多导致迭代步数增加,计算时间增加。然而,分区增多造成每个区域的规模减小,单步迭代的时间减小,且系统分区越均匀,即所有区域的单步迭代时间越接近,计算时间越小。从表中数据可知,随着系统分区数目的增加,平均迭代步数增加,平均计算时间增大,然而区域规模的减小对减小单步迭代时间的作用不甚明显。

4 结语

本文提出了一种基于多区域并行协同的多目标分布式帕累托最优潮流算法,并基于IEEE 118节点系统搭建仿真模型进行了验证,并得到以下结论。

1)算法克服了传统集中式优化方法的缺点,无须上层优化中心,将系统分解为多个区域,各区域独立完成本区域的优化,区域之间仅须交换少量的数据进行全局协调,有效保证了设备运行参数的私密性,比较适合开放电力市场环境下不同区域电网合作的协同调度。

2)算法将大规模多目标优化问题分解为几个小规模的优化问题,实现了分布并行的计算模式,减小了计算内存。该算法可根据系统互联区域个数改变算法结构,可拓展性强。

3)所提算法并不局限于多目标最优潮流的分布式帕累托求解问题,还可以推广到电力系统其他类似的优化问题中,具有较高的应用普适性。

4) 在所提的分布式多目标优化计算中,认为区域之间不存在利益博弈。在以后的工作中,将继续深入探讨考虑区域电网之间利益博弈的分布式优化计算问题。

本文得到国家自然科学基金(51477055)资助,特此致谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。