基于几何分布的微电网孤岛运行可靠性快速概率评估
张 杰, 管 霖, 黄振琳
(1. 华南理工大学电力学院, 广东省广州市 510641; 2. 广州大学机械与电气工程学院, 广东省广州市 510006)
0 引言
微电网(microgrid,MG)[1]存在并网运行和孤岛运行两种运行状态。其中,并网运行时存在主电源支撑因而供电充足,负荷能获得持续供电。当主网故障或受到扰动时,不乏持续数小时甚至10 h以上的停电存在,微电网切换为由分布式电源(distribution generator,DG)独立供电的短时孤岛运行。准确处理间歇性电源的波动性是孤岛运行可靠性评估的难点和热点[2-15]。另外,微电网孤岛运行往往需要采取负荷切除策略。实际运行中负荷频繁投切会对用电设备,尤其是电动机或电子类设备造成较大的冲击,损害设备寿命。对于存在光伏等波动性电源且电源总容量不足的微电网,诸如云层运动造成的光伏功率频繁跳变等因素均可能导致部分负荷被频繁投切,从而威胁用电设备安全。因此,实际工程中会尽量避免因电源的不稳定造成用电设备的反复投切。对于短时孤岛运行的微电网,实际可采取负荷切除后即不再投入的策略。这种实际的切负荷策略与源荷波动性使得孤岛期间各时间段的负荷状态具有了显著的时序关联性,因而微电网孤岛运行可靠性评估变得更为复杂。
时序蒙特卡洛仿真适合处理时序关联性问题[2-6],便于对运行中的各种复杂时序状态和操作进行统计分析从而得到可靠性指标的概率分布,然而时序蒙特卡洛方法存在计算量大的问题。为避免此问题,有学者对解析法[7-9]、点估计法[10-12]及混合法[13-15]进行了研究。文献[7]采用离散卷积计算负荷点的孤岛供电不足概率,文献[8]建立基于马尔可夫过程的DG多容量状态模型并通过短期分析法得到孤岛供电概率,文献[9]则基于聚类方法和场景削减技术得到典型源荷样本从而计算孤岛负荷切除概率,随后均采用全概率公式计算孤岛负荷点停电时间和停电次数指标。文献[10-12]采用点估计法构造输入变量样本点,文献[13-14]则采用非序贯蒙特卡洛仿真方法随机抽取源荷样本,通过对各样本点对应的确定性配电网运行状态进行评估从而得到可靠性指标。文献[7-14]将随机性问题转化为确定性的问题,用某一时间断面的源荷场景代替孤岛过程中连续波动的源荷状态,因而孤岛期间负荷切除操作明确从而简化了可靠性指标的求解。这种思路避免了时序蒙特卡洛仿真计算量大的问题。然而,这种负荷点停电时间的统计实际等同于在计及孤岛期间源荷功率波动的同时对负荷采取了实时投切的策略,这种实时投切策略导致负荷点频繁停电,不符合实际。文献[15]采用蒙特卡洛方法对微电网离网时间进行多次抽样得到系统可靠性指标,是一种较好的评估思路,但依然存在仿真时间较长的问题。
针对上述问题,本文考虑孤岛期间的源荷波动性和实际切负荷策略,提出了一种微电网孤岛运行可靠性快速概率评估方法,以下简称为快速概率评估方法(fast probabilistic evaluation method,FPEM)。该方法以源荷相关性样本为基础,首先计算孤岛内的负荷损失概率,随后采用基于几何分布模型推导的解析计算公式快速计算负荷点停电时间概率分布,最后综合出负荷点和系统停电频率与停电时间可靠性指标。
1 FPEM框架和特点
适用于微电网孤岛运行可靠性指标计算的FPEM框架如图1所示。
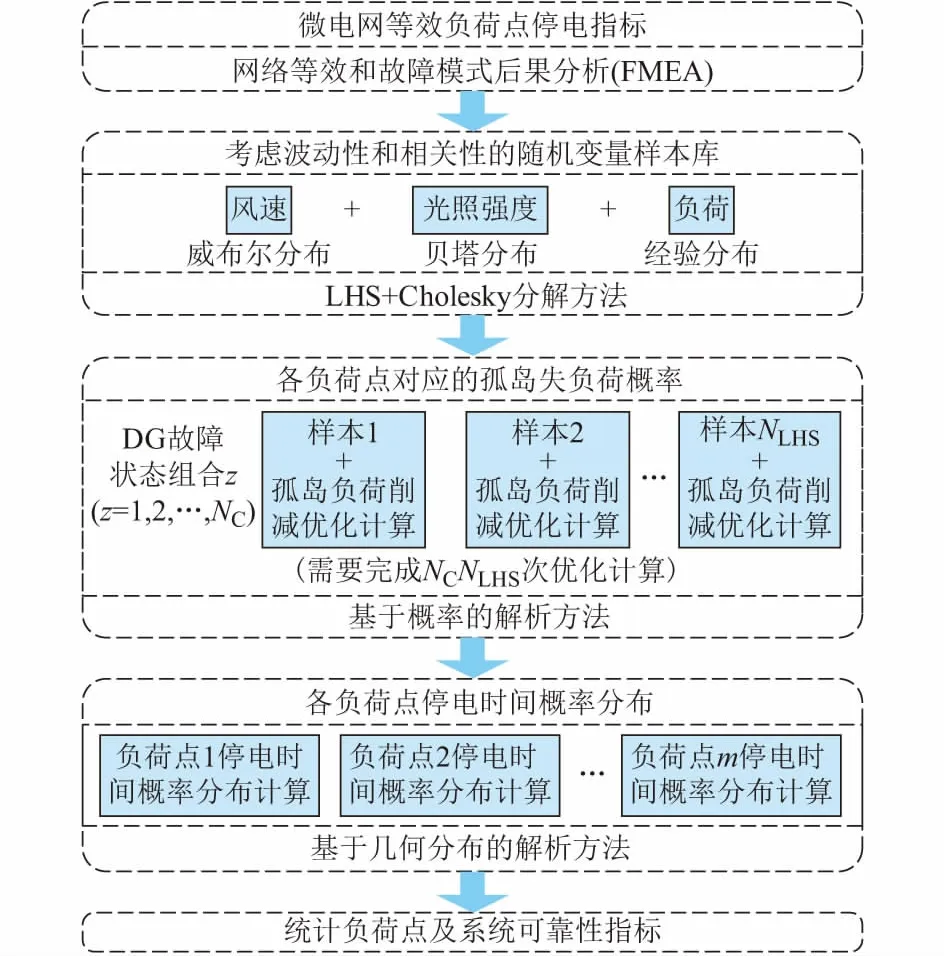
图1 FPEM的框架Fig.1 Framework of FPEM
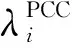
1)建立适合的DG和负荷功率的随机分布概率模型。应用拉丁超立方抽样(Latin hypercube sampling,LHS)和Choleskey分解得出DG和负荷相关性样本矩阵,记样本数为NLHS。
2)对前一环节中的每一个样本,进行孤岛电源充裕度评估,并根据DG停运状态组合(记组合总数为NC)应用NCNLHS次孤岛负荷削减优化计算得出各负荷点的孤岛失负荷概率。
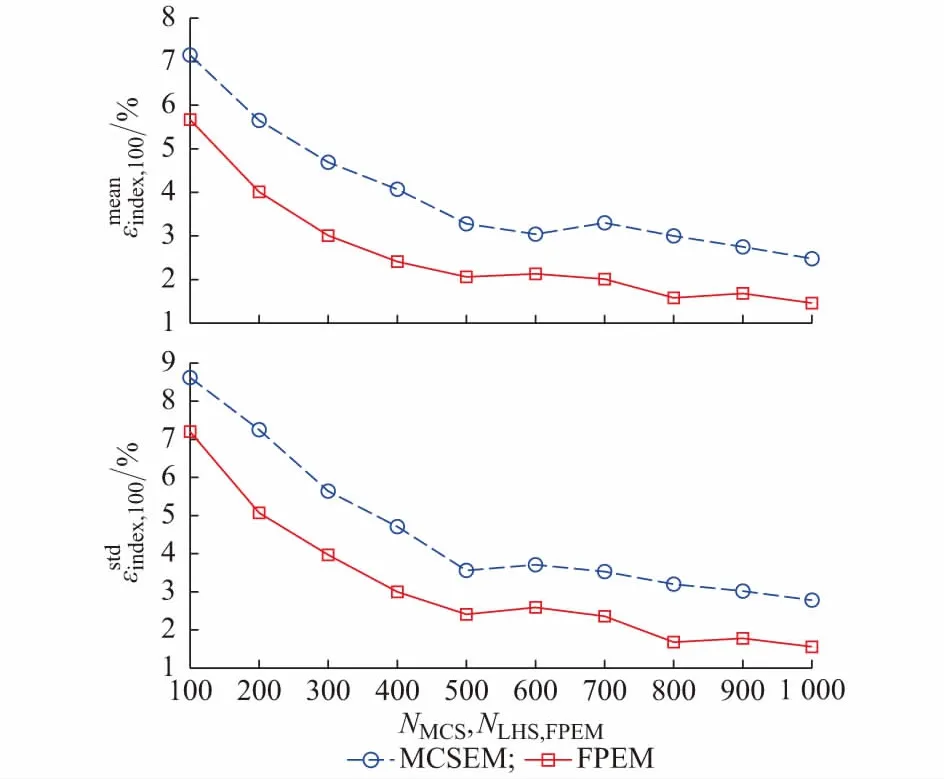
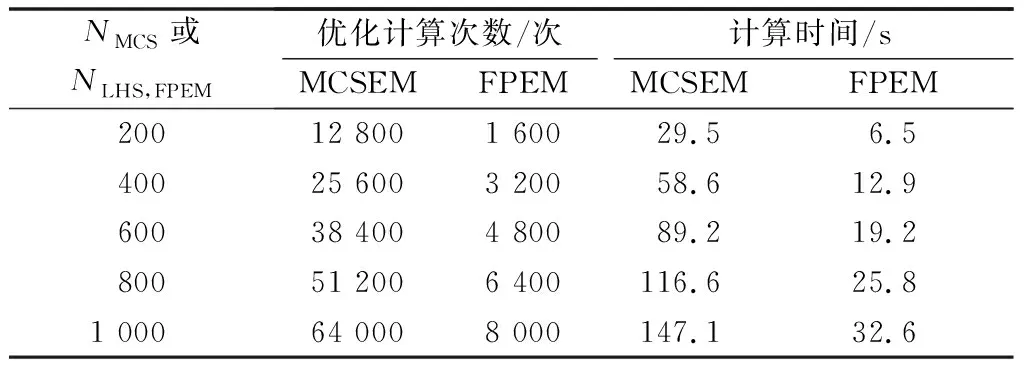
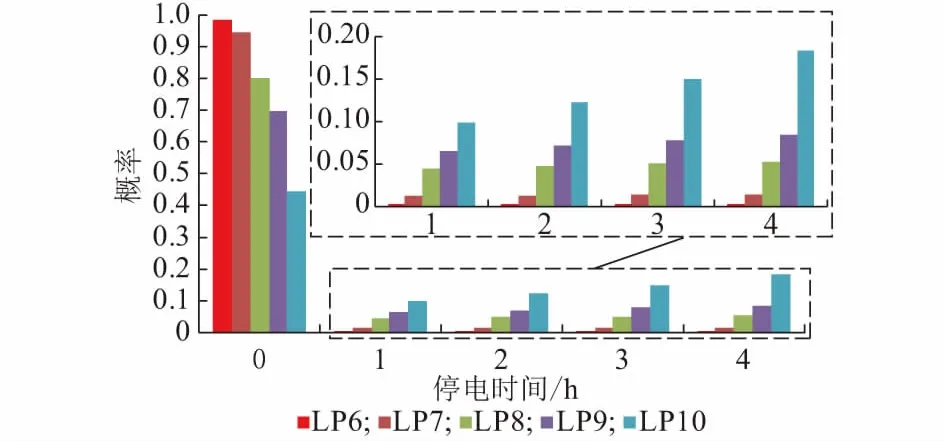
3)针对负荷一旦在某个时间段t(0 由于所采用的切负荷策略和源荷波动性使孤岛期间各时间段的负荷状态具有了强时序关联性,要得出孤岛期间的负荷点可靠性指标通常适宜采用时序蒙特卡洛方法,然而为减少仿真计算量可借鉴文献[15]采用一种基于蒙特卡洛仿真的估计法(Monte Carlo simulation evaluation method,MCSEM),其核心算法见图2。图2算法实现图1的FPEM中红框部分完成的功能,即针对每个DG停运状态组合对微电网离网时间进行NMCS次重复仿真模拟,每次仿真均对Tmax个时间段(其中Tmax=max{Ti})依次从预先生成的随机变量样本库中随机抽样进行孤岛负荷削减优化计算,最终得到微电网中各负荷点停电时间的概率分布。则MCSEM的优化计算总次数为NCTmaxNMCS次。而FPEM中负荷削减优化次数则为NCNLHS次。负荷优化计算耗时是可靠性评估算法程序的主要耗时环节,在保证相同计算精度的前提下NMCS与NLHS数量相当,因此FPEM可有效缩短可靠性指标计算时间。 图2 MCSEM的核心算法Fig.2 Key algorithm of MCSEM 本文第2节介绍随机模型选取和相关抽样算法,第3节简介电源停运组合概率模型,第4节重点介绍图1红框对应的负荷点可靠性指标快速计算公式和方法,第5节通过实例对比验证算法的有效性。 长时间尺度的可靠性评估中,风速v可用双参数威布尔分布描述,标准光照强度H可用贝塔分布描述。微电网覆盖区域小,对微电网内的同一类电源(如风电、光伏)可采用相同的功率分布。虽然在某个确定运行方式下,负荷可视为以预测值为均值的正态分布,但在年统计尺度上则不适合采用正态分布。尤其微电网中负荷类型相对单一,可靠性统计期间的负荷分布往往并不服从常见的概率分布,为此,可采用经验分布函数描述负荷[16]。 无论日照、风速还是人类作息时间都存在天然的相关性,均受到地球的自转及公转运动、大气层运动的影响,因此风电、光伏和负荷功率在一天及更长时间尺度的变化存在内在的强相关性。文献[2,12-14,17]研究表明源荷相关性对配电系统可靠性有显著的影响。因此,在微电网状态抽样时必须考虑三者的相关性。本文采用LHS[18]和Choleskey分解排序[19]得到具有目标相关性的样本矩阵S,该矩阵包含NLHS个由风速、标准光照强度和负荷组成的样本Sj(详见附录A)。 (1) 式中:Ωf和Ωg分别为第z个DG状态组合下处于失效状态的DG集合和工作状态的DG集合。 对风光荷样本Sj,对应停运状态组合z,NR台间歇性可再生DG的有功出力之和为: (2) 式中:函数Ci(ei)为第i台DG的有功出力与其一次能源ei之间的函数关系。其中,风电机组出力与风速之间具有非线性关系,可采用风电机组功率曲线[20]描述该函数。光伏电源出力与光照强度之间则具有近似线性关系[21],即Ci(·)为线性函数。 微电网内一般还包含柴油发电机组、燃气轮机组等可控型DG,以便增强微电网孤岛运行状态时的电能供给可控性。由于这些设备多在孤岛运行时才投运,运行状态相对稳定,且孤岛运行时间一般较短,可认为孤岛运行期间这类可控型DG的故障概率为零,其DG功率模型为: (3) 并网型微电网如设有储能单元,小容量储能在短时孤岛运行时采用Vf控制[15],其功能主要针对负荷和波动性电源分钟级以内的波动,以稳定电压和频率。这类储能则不宜纳入可靠性评估的电源范畴。 由此,微电网总有功出力为: (4) 当微电网孤岛运行时,一旦发电出力不能满足负荷需求,一般根据负荷点的重要性等级采取负荷分级削减策略。例如文献[7]以满足岛内负荷供电需求最大化为原则,根据负荷点权重采取优化计算做出负荷削减决策。为了更为精细地反映微电网用户的可靠性,本文对不同优先级的负荷点分别计算其孤岛失负荷概率指标。 (5) 式中:Il,j,z取值为0或1,取0表示输入变量计算样本为Sj、DG处于状态组合z时,负荷点l被切除,取1表示负荷点l没有被切除。 Il,j,z由以下决策模型决定: (6) 对每个样本Sj枚举DG停运状态组合z逐一执行负荷削减优化计算后,可得微电网孤岛状态下负荷点l的停电概率指标为: (7) (8) (9) (10) (11) 同理,如果孤岛状态下负荷点l获得DG持续供电时间不少于Ti个Δt,则该负荷点不停电(即r=0),其概率为: (12) 式(11)与式(12)构成微电网外部元件i故障后微电网内负荷点l停电时间的概率分布。 (13) (14) 由上述可靠性指标可综合得出SAIFI和SAIDI等微电网系统可靠性指标,具体公式为: (15) (16) 式中:NL为微电网内负荷点个数;NE为配电网中影响微电网供电的元件个数;Nl为负荷点l的用户数。 本文算例由IEEE RBTS-Bus 6配电系统[23]中的馈线1改造而来,即在馈线1的负荷点LP6位置设置一个低压微电网(见附录B图B1)。该微电网中:设置2台相同型号的风电机组,其额定功率均为375 kW,切入风速为4 m/s,额定风速为12 m/s,切出风速为22 m/s,强迫停运率为0.05;设置一套光伏发电机组,其额定功率为750 kW,强迫停运率为0.04;设置一台柴油机组,额定功率为100 kW;设置一组15 kW蓄电池。微电网设置5个负荷点LP6至LP10,负荷点用户数均为1,功率峰值均为200 kW,其负荷优先级系数依次为0.3,0.25,0.2,0.15,0.1。 不计微电网内网络元件和开关的故障。微电网外14条线路出现故障都将导致微电网离网孤岛运行。线路的基础可靠性参数参考文献[24]。其中线路1的修复时间(8 h)最长,即Tmax=8。 假设微电网内的风速满足形状参数k为3.97、尺度参数c为10.6的双参数威布尔分布,光照强度满足分布参数α为2.06、β为2.5的贝塔分布。微电网负荷数值上采用IEEE RTS-96系统年度时序负荷曲线[25]中的负荷数据。分析发现该负荷数据分布为多峰曲线,并不服从常见概率分布,因此采用经验分布函数描述该负荷分布。微电网内风速、光照强度和5个负荷(按风速、光照强度和负荷点6至10依次排列)的秩相关系数矩阵为: (17) 为验证第4节推导的负荷点停运时间分布解析公式的正确性和有效性,将其与第1节的MCSEM进行计算结果和计算时间的对比。2种算法采用相同的方式产生输入变量相关性样本作为样本库。 首先,采用MCSEM,取LHS采样规模NLHS,MCSEM为5 000次、仿真次数NMCS为50 000次,进行可靠性计算。将得到的可靠性指标结果记为Ia。因该结果是在较大样本规模和仿真次数下获得的,可视为精确结果,作为与其他计算结果的对比基准。描述微电网可靠性的指标较多,本文采用常用的SAIFI和SAIDI构成Ia。 然后,采用不同LHS采样次数NLHS,FPEM应用FPEM计算微电网的SAIFI和SAIDI。考虑计算结果具有一定的波动性和随机性,重复计算100次。记第j次的指标计算结果为Is,j,按下式计算相对误差: 100% (18) 图3 FPEM与MCSEM的误差特性比较(Tmax=8)Fig.3 Error characteristic comparison between FPEM and MCSEM (Tmax=8) 从图3(a)和(b)可见,随着NLHS,FPEM次数的增加,FPEM的计算精度不断提高。但LHS抽样数达到500后,误差下降减缓,超过800后误差基本不再下降。方差也具有同样的规律,表明LHS的抽样数达到500后多次重复计算的结果非常接近,可无需多次重复计算。图3表明,MCSEM的精度与仿真次数NMCS密切相关。当NMCS<1 000时(对比标准为50 000)其误差较大,且误差总是大于相同NLHS,FPEM次数的FPEM的计算结果。 根据第1节的分析,FPEM算法的优化计算次数为NCNLHS,FPEM次,而MCSEM的优化计算次数为NCTmaxNMCS次,因此当NLHS,FPEM=NMCS时,FPEM算法不仅计算精度明显优于MCSEM,而且计算时间远小于后者。表1给出了Tmax=8的情况下2种算法完整过程的优化次数和计算时间统计(采用普通计算机)。可以看出由于FPEM算法的优化次数较MCSEM大幅减少,其计算时间约为MCSEM的1/5~1/4。 表1 FPEM与MCSEM的计算时间对比(Tmax=8)Table 1 Comparison of computation time between FPEM and MCSEM (Tmax=8) 此外,MCSEM的计算时间还正比于微电网最大离网时间Tmax,而本文提出的FPEM基本不受Tmax的影响,见附录B表B1。为进一步考查Tmax不同时FPEM的适用性,分别取Tmax为12,16,20,采用同样的过程进行微电网可靠性指标计算和比较。结果表明两种算法的计算精度基本不受Tmax变化的影响。 采用FPEM算法不仅能获得孤岛失负荷概率指标,还能计算出微电网内不同负荷点的停电时间概率分布。以算例中线路3故障为例,经分析知线路3故障时微电网等效负荷点的停电时间为4 h。采用FPEM评估微电网孤岛运行4 h的负荷点可靠性,可得到线路3故障时微电网内各负荷点停电时间的概率分布如图4所示。 为进一步验证所提可靠性指标计算模型处理源荷波动和采用实际切负荷策略的合理性,研究孤岛期间源荷波动与切负荷策略对微电网孤岛可靠性的影响,对比分析以下3种情况下的可靠性指标。 图4 线路3故障时微电网负荷点停电时间的概率分布Fig.4 Probability distribution of power outage time at microgrid load point when line 3 fails 案例1:考虑孤岛期间源荷功率波动并采用负荷削减后不再投入的策略,采用FPEM计算(NLHS,FPEM为1 000次)。 案例2:计及源荷随机分布但假定孤岛期间源—荷功率恒定,采用文献[7-14]的思路求解指标。 案例3:计及孤岛期间源荷波动性并对负荷采取实时投切策略,采用MCSEM计算(NLHS,MCSEM与NMCS分别为5 000次和1 000次)。 经计算,案例1、案例2、案例3这3种方案下微电网SAIFI依次为0.273 1,0.076 8,0.332 5,SAIDI依次为0.830 4,0.336 1,0.340 6。可以看出,案例2和案例3下的SAIDI几乎相同,说明不考虑孤岛内源荷波动与考虑其波动并且采取负荷实时投切这两种情况下的停电时间相同,且均与案例1的SAIDI相差约60%,停电时间统计值偏小;SAIFI方面,案例2相比案例1的指标相差67.6%,说明孤岛内源—荷波动实际上会导致负荷停电次数较多,案例3相比案例1的指标又增加了21.8%,说明对负荷采取实时投切导致负荷点停电次数更多,其中供电优先级别较低的负荷会频繁遭遇停电。显然,孤岛期间源荷功率的波动和切负荷策略对微电网可靠性指标影响较大,案例1的计算结果更为合理。本文提出的计算模型采用了实际的切负荷策略同时可准确描述源荷波动性,其计算结果更符合实际。 孤岛期间源荷功率波动性和避免负荷频繁投切的负荷优化控制策略使得负荷状态具有很强的时序关联性。为避免传统方法仿真计算量大的问题,本文基于几何分布模型和概率计算,推导了快速准确地计算微电网负荷点停电时间概率分布的解析公式。方法综合考虑了间歇性DG的故障、间歇性电源和负荷功率的波动性与空间相关性。算例表明,所提方法不需要大量的仿真计算就能得到与采用蒙特卡洛仿真方法相近的计算结果,而且能得到负荷点停电时间指标的概率分布情况,计算效率大大提升。本文准确考虑源荷波动并采用实际切负荷策略的计算结果符合实际。后续将综合考虑源荷功率的时空相关性以及微电网内大容量储能装置参与能量平衡对可靠性的影响,展开进一步研究。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 (编辑蔡静雯)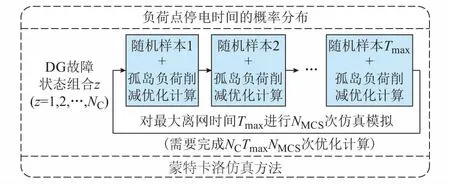
2 源荷随机分布模型和相关性抽样
2.1 常见随机变量的分布模型
2.2 随机变量相关性样本库
3 微电网有功出力模型
3.1 间歇性可再生DG停运状态组合及其功率
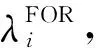
3.2 可控型DG功率模型
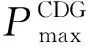
4 微电网孤岛可靠性快速概率评估
4.1 孤岛失负荷概率指标评估
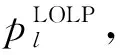

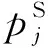
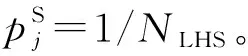
4.2 微电网可靠性指标评估
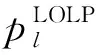
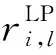
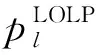
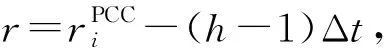
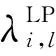
5 算例分析
5.1 算例参数
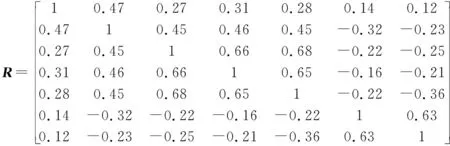
5.2 FPEM与MCSEM的对比验证
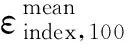
5.3 源荷波动与切负荷策略对可靠性的影响分析
6 结语

