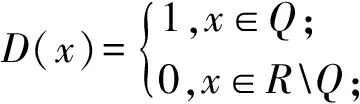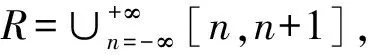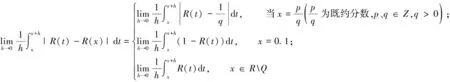近似连续点与Lebesgue点的性质及其应用
黄政,刘志杰
(贵州师范大学 贵州省信息与计算科学重点实验室,贵州 贵阳 550001)
0 引 言
在科学计算、大数据智能分析、点云计算以及安全模型设计等应用领域,在构建数学模型过程中,结合函数与相关的数值算法,对相应的数据进行处理,其中近似连续点与Lebesgue点作为函数性质里的重要内容,值得系统分析.现进一步总结与讨论函数的近似连续点与Lebesgue点的性质和推广,优化分析方法,并讨论一些具体应用.
1 预备概念
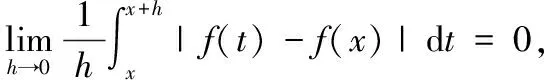
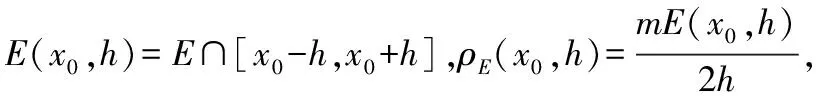
注:由于0≤mE(x0,h)≤m{[x0-h,x0+h]}=2h,因此0≤ρE(x0)≤1,显然,对于满足0<ρE(x0)<的点x0,既不是f(x)的稠密点也不是其稀薄点.
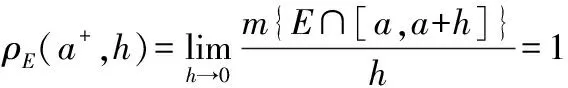

定义5[2]设函数f(x)定义在闭区间[a,b]上,设x0∈[a,b].若在[a,b]中存在可测集E,以点x0为其稠密点,且f(x)限制在集E时在点x0处连续,则称在f(x)点x0处近似连续,点x0称为f(x)的一个近似连续点.
2 主要结论

定理2Lebesgue可积函数的所有连续点都是Lebesgue点.
证明:结合函数连续性的定义以及定义1显然可证得.
注:该定理的逆命题不成立,即Lebesgue可积函数的Lebesgue点不一定是连续点.例如在例3.1中的Dirichlet函数D(x)在R中Lebesgue可积,且在任意点处极限不存在,在R中处处不连续,因此在无理数集RQ也不连续,但其Lebesgue点集为无理数集RQ.另外,任意函数的任一孤立点一定不是Lebesgue点.
定理3对于任意可积函数,若存在一阶不可去间断点,则该间断点必定为非Lebesgue点
注:对于第二类间断点,则可能为Lebesgue点.例如在例3.1中的Dirichlet函数D(x)在R中处处不连续,间断点为第二类间断点,其Lebesgue点集为无理数集RQ.
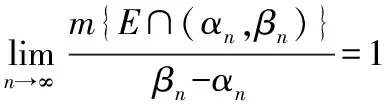
证明:可结合可测集的定义以及定义2进行证明.
定理5[3]任意函数的连续点必为近似连续点.
注:显然,任意函数的任一孤立点一定不是近似连续点.函数的近似连续点不一定是连续点.(可见结论2.6的注中的例子).由文献[3]可知:可测函数可以没有连续点.在定理6的注中,便是一例子.
定理6函数f(x)∈L1([a,b]),则闭区间[a,b]中的点几乎都是Lebesgue点.
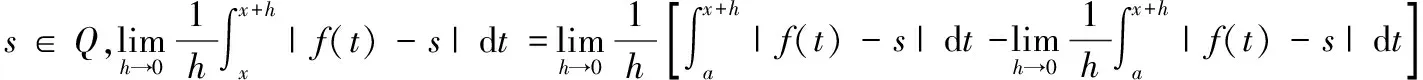
现可证明:集合[a,b]G中的点都是Lebesgue点.
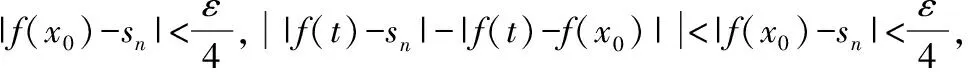
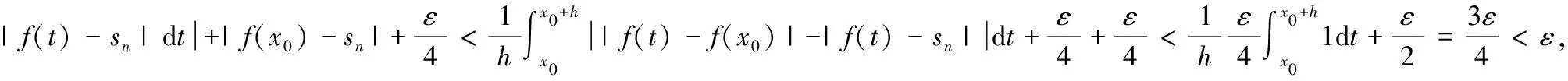
注:由该定理知:闭区间[a,b]上的Lebesgue可积函数f(x),其所有Lebesgue点所构成的集合必为稠密集.结合文献[5],又由于稠密点一定是凝聚点,故Lebesgue点所构成的集合必为聚集.由于孤立点一定不是稠密点,故任意函数的定义域中任一孤立点均不是Lebesgue点.
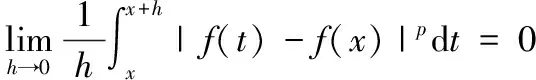
证明;方法类似定理6的过程.
注:对于p=1,即为结论2.6的情形.而对于0 定理7对于任意Lebesgue可积函数f(x),其所有Lebesgue点都是近似连续点. 先证明:函数f(x)限制在集H上时在点x0左连续. f(x)限制在集H2上时在点x0右连续.因此,点x0为f(x)限制在集H1∪H2上的连续点. 现在证明点x0为f(x)限制在集H1的左稠密点. 对于∀h>0,且h 注:上述命题的逆命题则不成立.即存在Lebesgue可测函数,其某个近似连续点不是Lebesgue点.现构造函数 可以证明点x=0是f(x)的近似连续点,但不是Lebesgue点,也不是连续点. 若对Lebesgue可积函数f(x)适当加强条件,则可以使其所有近似连续点都是Lebesgue点.下面的结论2.6[3]便是其中一个情形. 定理8有界可测函数的Lebesgue点集合与近似连续点集合是相同的. 证明:由上述结论2.5[3]可知:可测函数的Lebesgue点必为近似连续点;现只需要证明:可测函数在“有界”限制下,近似连续点必为Lebesgue点即可. 例2 对于R上的Riemann函数,定义为 结合文献[5]-[7]分析可知,对于R(x)定义在R时,在x=0,1及一切无理点处连续,而在R内的一切有理点处间断.因此其Lebesgue点集为RQ,而非Lebesgue点集为Q,由于点集Q为可数集且mQ=0,从而R中几乎所有的点为Lebesgue点.由定理5可知:在R内一切无理点都是R(x)的近似连续点.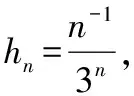
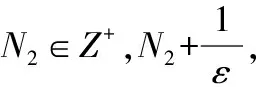
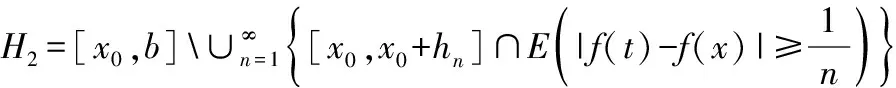
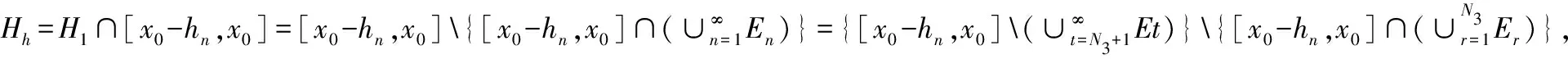
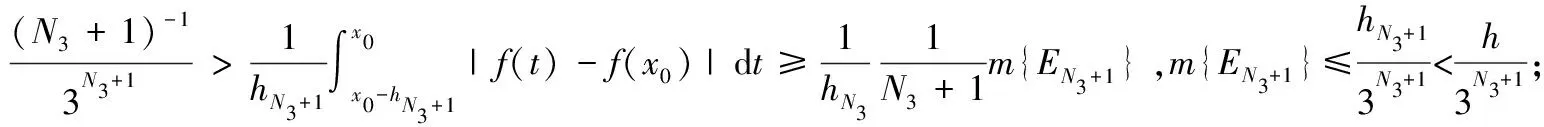
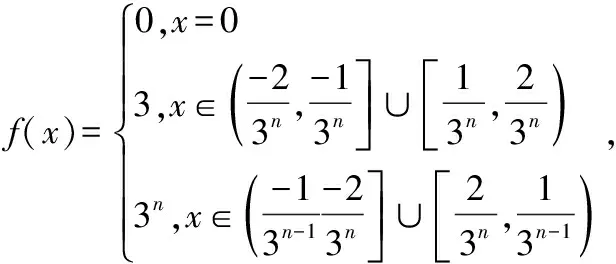
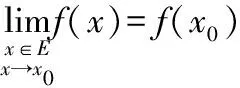
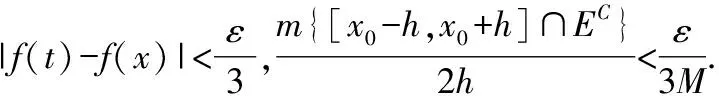
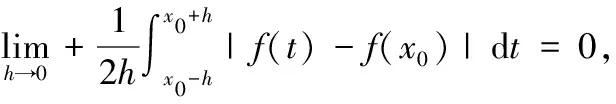
3 应 用