基于SVR的隐形眼镜销量预测方法

徐时伟

（温州职业技术学院 信息技术系，浙江 温州 325035）

0引 言

在隐形眼镜销售链中，上游批发商、下游零售商以小企业或个体户为主，受管理水平与资金所限，所使用的销售管理软件功能较为简单，仅有进销存记录与客户管理等基本功能，缺乏数据分析及预测功能。这类软件以单机版居多，易造成销售链上下游的数据互相孤立，上游无法根据下游经营预期及时调整库存与供货。基于此，对隐形眼镜销量进行分析与预测，对上下游商家均有重要意义。

在销量预测研究方面，比较成熟的技术有线性回归、ARIMA等时间序列模型，但模型中缺少对外部因素的考虑。随着人工智能的发展，神经网络被应用于复杂的非线性回归问题[1]，但需要足够多的样本，且存在易过拟合、推广能力差等缺点。SVR（Supported Vector Regression）是一种基于统计学习理论的机器学习方法，弥补了神经网络的缺点，适用于小样本情况下的多维非线性回归预测问题[2]。本文提出一种基于SVR的隐形眼镜销量预测方法，并应用于“云镜”在线隐形眼镜进销存管理系统[3]。该系统以“打通上下游，构建直采生态”为特色，为本文实验提供了原始数据，而其研究结果又有助于该系统上下游商家提升精细化管理水平。

1隐形眼镜销量预测系统

1.1 系统结构

原“云镜”系统包括进销存管理、客户管理、采购管理、数据分析报表等4个模块，将基于SVR的隐形眼镜销量预测模块与之集成后，系统结构如图1所示。基于SVR的隐形眼镜销量预测模块在每日凌晨系统空闲时段读取数据库中数据进行离线预测，将结果写回数据库。下游零售商访问数据分析报表模块，可查看其店铺中各品牌隐形眼镜的销量预测结果，而上游批发商则可查看与之有采购关系的零售商销量预测结果总和。

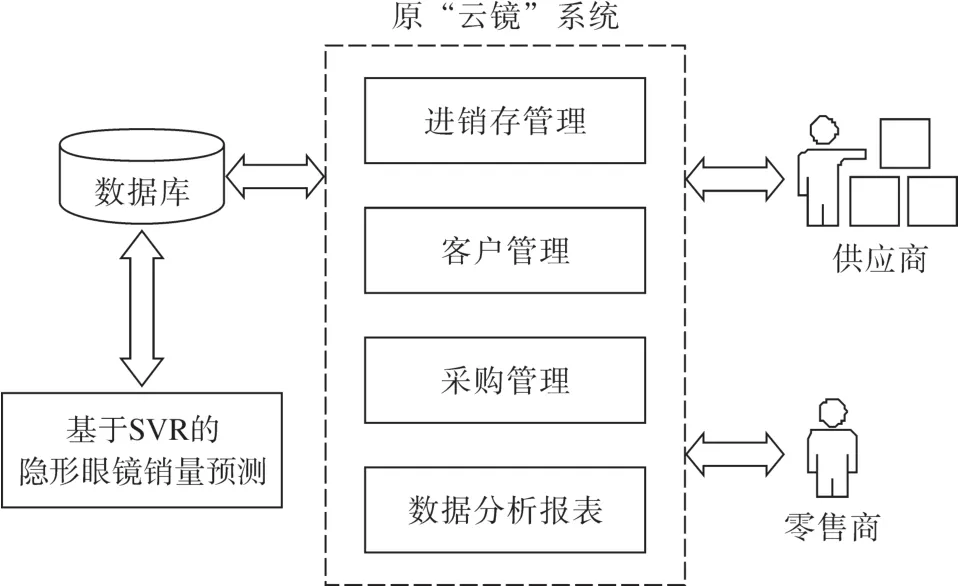
图1 隐形眼镜销量预测系统结构

1.2 销量预测模块流程

本文对“云镜”系统中每个零售商的每个隐形眼镜品牌进行销量预测。隐形眼镜销量预测模块流程如图2所示。从数据库中读取预测所需的原始数据，经过模糊化和归一化等预处理，然后从中提取特征向量，进行SVR，最后得到预测结果并写回数据库。

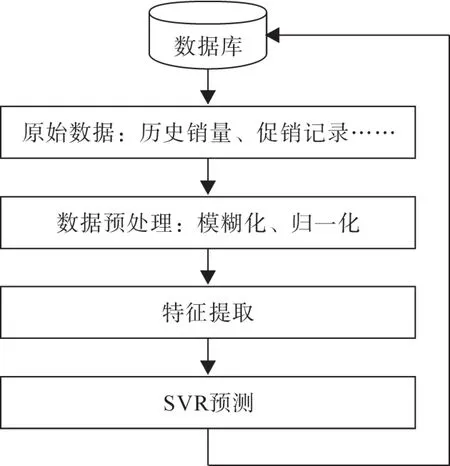
图2 隐形眼镜销量预测模块流程

2基于SVR的隐形眼镜销量预测原理

2.1 SVR基本原理

Vapnik等提出的支持向量算法，以结构风险最小化为目标，克服了神经网络可能出现的局部极小、过学习等问题[4]。支持向量算法在文本分类、模式识别等分类问题领域应用广泛，在回归预测领域也有应用场景。其基本思想是：通过非线性映射，把样本空间映射到一个高维特征空间，使得在特征空间中可应用线性学习机的方法解决样本空间中的高度非线性分类和回归问题[5]。具体到回归预测领域，假设有一个训练样本数据集(x1,y1,)(x2,y1,) …, (xn,yn)，其中xi∈RN为N维输入向量，yi∈R为目标值。我们希望学习到一个函数f(x)=wgΦ(x)+b，使其与y尽可能接近，其中Φ(x)为从RN空间到高维空间的某种非线性变换。寻找最优f(x)的问题可转化为：

其中，It( )为损失函数，C为惩罚参数。引入松弛变量和，可转化为：

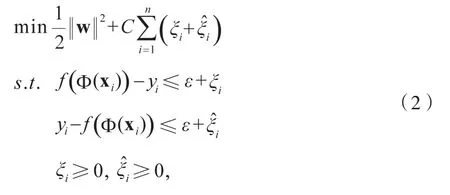
引入拉格朗日乘子，得到对偶问题，求解后得到回归函数为：

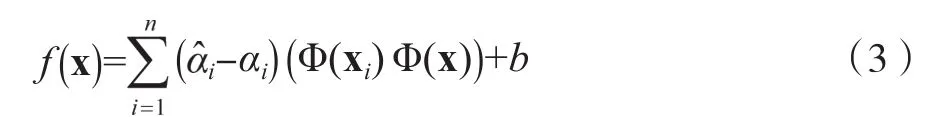
为了简化计算，用样本空间中满足Mercer条件的核函数K(xi, x)代替高维空间中的内积运算，（3）式可转化为：

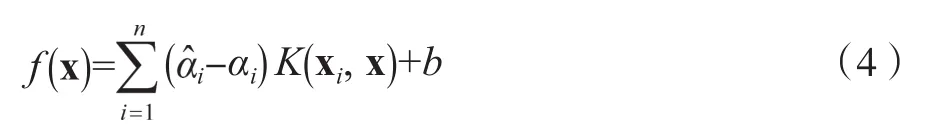
2.2 特征向量

本文考虑隐形眼镜销售特点，综合“云镜”系统用户的调查反馈意见，选择代表内部因素和外部因素的多个特征向量。其内部因素为前N个周期的销量x1, x2, x3, …, xN；外部因素包括月份xmonth、当前周期是否有节假日xholiday、当前周期是否有促销活动xonsale、接近过期比例xexprate。因特征向量中含有非数值变量，且不同类型的变量量纲不同，在进行SVR训练前，需要对数据进行模糊化和归一化处理，即：

2.3 预测误差

对于一家零售商，假设其在售的隐形眼镜品牌数为m，第j个品牌的销量预测值为p1,j,p2,j,…,pn,j及实际值为o1,j,o2,j,…,on,j，其中n为周期数。定义预测误差的计算公式为：

第j个品牌的单品牌预测误差为：

全品牌预测误差为：

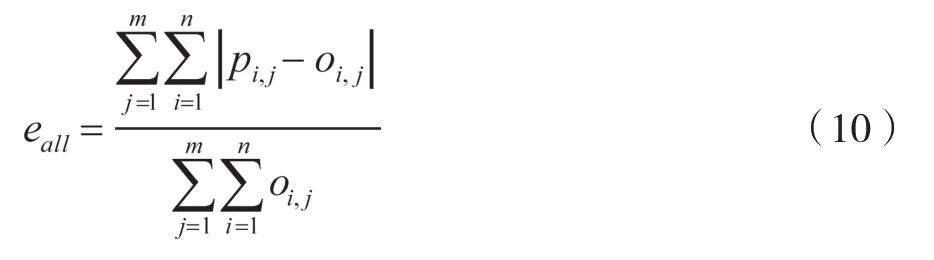
每个零售商依（9）、（10）式计算后取平均值，作为全部零售商的整体预测误差。

3实 验

3.1 实验设计

以“云镜”系统中的销售数据为基础，进行训练与预测实验。以一个星期为周期，将系统中所有隐形眼镜零售商近两年共96个周期的销售数据作为样本集，选取前72个周期用于训练，后24个周期用于测试。使用Python机器学习工具包scikit-learn，核函数选用径向基函数，进行单品牌测试和全品牌测试，依（9）、（ 10）式计算各测试误差。

在SVR中，特征向量的选择会影响预测准确度。在实验中，先选择销量最大零售商，针对特征向量中内部因素和外部因素，分别选取不同的参数或组合进行模型训练，比较误差结果，确定最优特征向量；然后再对全部零售商进行销量预测，分析整体预测误差。本实验的原始数据为销量最大零售商和全部零售商的某3种典型品牌隐形眼镜销售数据（见表1～表2）。

表1 销量最大零售商的3种品牌隐形眼镜销售数据

表2 全部零售商的3种品牌隐形眼镜销售数据

3.2 实验结果与分析

单品牌测试与全品牌测试中，误差随历史周期数N变化的关系见表3。由表3可知，N太小，则不能有效体现近期销量的影响；N太大，则存在信息冗余。因此，选择N=6进行后续实验。

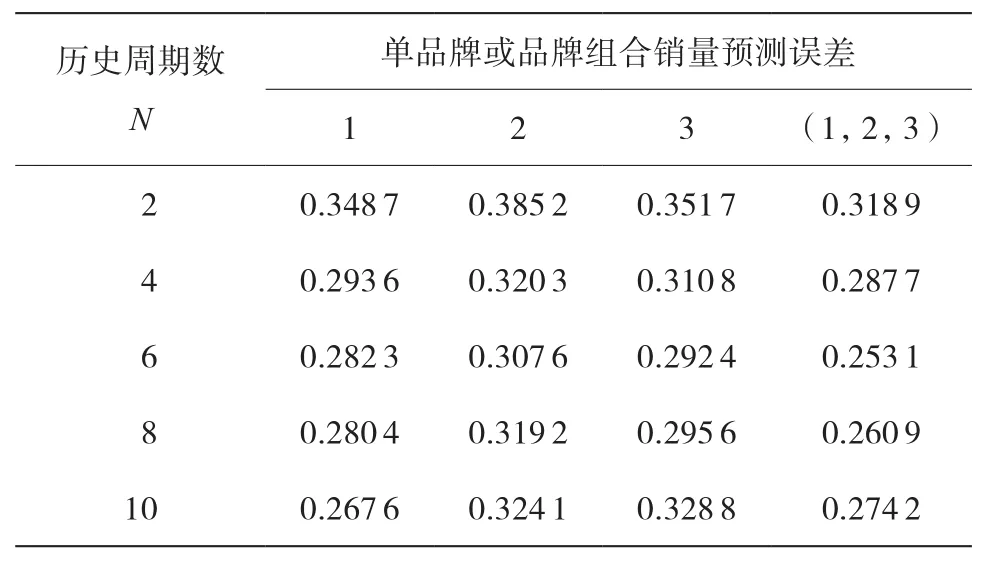
表3 3种品牌隐形眼镜销量预测误差—历史周期数 N 变化的关系

单品牌测试与全品牌测试中，不同外部因素组合对误差的影响见表4。由表4可知，加入月份会增加预测误差，加入节假日信息对预测结果影响不大。是否有促销、接近过期比例能减小预测误差，且二者组合能取得相对较好的结果。

表4 3种品牌隐形眼镜销量预测误差—外部因素组合关系

经过实验筛选，确定最优特征向量。为了进一步检验该方法的准确性，采用线性回归方法、ARIMA方法进行隐形眼镜销量预测，比较不同方法的品牌隐形眼镜销量整体预测误差（见表5）。由表5可知，基于SVR的隐形眼镜销量预测方法的误差比线性回归方法降低34.99%[（0.3475—0.2259）/0.3475]，比ARIMA方法降低33.17%[（0.3380—0.2259）/0.3380]。

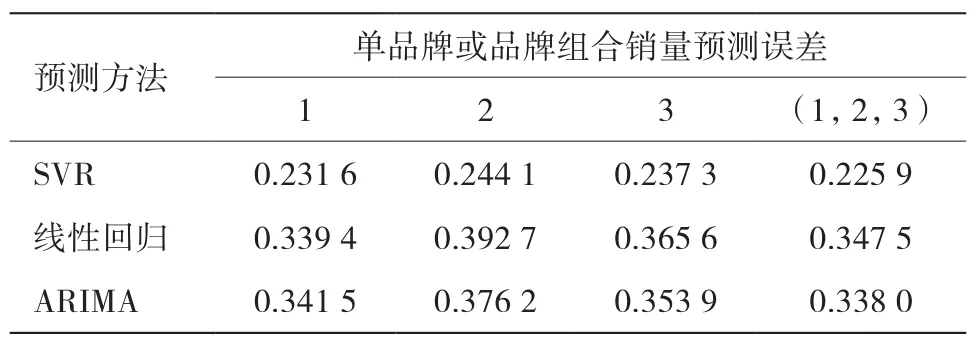
表5 不同方法的3种品牌隐形眼镜销量整体预测误差

4结 论

本文提出一种基于SVR的隐形眼镜销量预测方法，并应用于“云镜”在线隐形眼镜进销存管理系统中，对系统中各零售商的品牌隐形眼镜销量进行预测实验。实验结果表明，该方法相较于线性回归方法、ARIMA方法，预测误差最小，将有助于上下游商家合理安排采购计划及库存，提升精细化管理水平。同时，该方法综合考虑了时间序列这一内部因素和影响经营的诸多外部因素，且借助SVR的小样本适应性，较好地实现了历史数据较少情形下的回归预测。对于具有类似特点的预测问题，均可采用该方法。如其他商品的销量预测，可取近期销量数据作为内部因素，并结合该商品经营特点，引入多种可能影响销量的外部因素，通过实验筛选，确定最优特征向量。为了进一步提升预测的准确性，下一步研究将尝试人工智能领域的新算法，如深度学习等的应用。