基于时滞LQR算法的风洞模型振动控制试验研究*

张家昆, 贾振元，刘 昱，刘 巍，刘惟肖，姜雨丰，鲁继文

(大连理工大学 机械工程学院，辽宁 大连 116023)

风洞试验是飞行器设计开发的重要环节，是研究飞行器模型空气动力学特性的重要手段之一。出于减小对模型周围流场影响的考虑，风洞试验中飞行器模型一般采用尾部支撑的方式。风洞模型通过置于模型尾部的测力天平与支杆相连，支杆固支端和风洞弯刀利用销孔联接，通过调节风洞弯刀的上下移动来控制飞行器模型相对气流迎角大小。风洞模型—测力天平—风洞支杆构成低刚度的悬臂梁系统，在宽频带气动载荷激励以及飞行器模型空气动力学特性的共同作用下，该悬臂梁系统低阶共振被激发，试验时产生低频、大振幅的振动。该振动会导致所测数据不准确，甚至试验被迫中止，因此解决风洞试验中模型振动的控制问题显得尤为重要和迫切。

基于压电陶瓷作动器的振动主动控制是抑制风洞模型振动的有效方法。国内外学者针对该振动控制系统中压电陶瓷作动器的控制方法做了大量的研究。孙华亮等研究了神经网络ERA模型辨识振动系统，并利用神经网络PID实现了自适应振动控制[1]。宋静等提出了混合型迭代学习控制算法，在未知系统具体动力学参数的前提下实现了主动抑制[2]。佘重禧等分别设计了LQG及H∞控制算法，实现了对模型的低频振动控制[3]。聂旭涛等在压电组件嵌入式风洞模型支撑系统振动主动控制仿真中，建立了压电组件嵌入式结构有限元模型，并结合传统PID控制方法，实现了系统主动振动控制仿真[4]。S.Balakrishna等利用测力天平的信号作为反馈信号，结合传统比例微分控制，实现了抑制模型振动、提高试验迎角的目的[5]。

本文针对风洞模型振动抑制问题，分析了风洞模型—测力天平—风洞支杆悬臂梁系统的振动原因及振动特性，通过地面试验求解系统传递函数，建立系统的二阶模型。利用该二阶模型设计线性二次型最优控制算法，针对因振动加速度信号在反馈控制中的滤波环节导致的时滞问题，利用基频傅里叶变换与相位对比分析实现时滞的辨识，设计基于时滞补偿的线性二次型最优控制算法，并通过地面试验进行验证。

1 压电陶瓷作动器振动抑制系统

1.1 风洞模型—测力天平—风洞支杆悬臂梁系统

为尽可能减小支杆对风洞天平测力数据的影响，风洞试验中的模型采用尾部支杆支撑的方式。如图1所示，风洞模型、测力天平与尾撑支杆之间通过销孔配合联接，支杆尾端作为固支端固定于风洞弯刀部。风洞弯刀不仅起到固定整个悬臂梁系统的作用，通过调节风洞弯刀的上下移动可控制飞行器模型相对于气流迎角大小，从而实现不同迎角条件下的风洞试验[6-7]。通过安装在支杆后端直线段的压电陶瓷作动器，输出与支杆弯曲方向相反的反向力矩，实现对模型振动的控制。

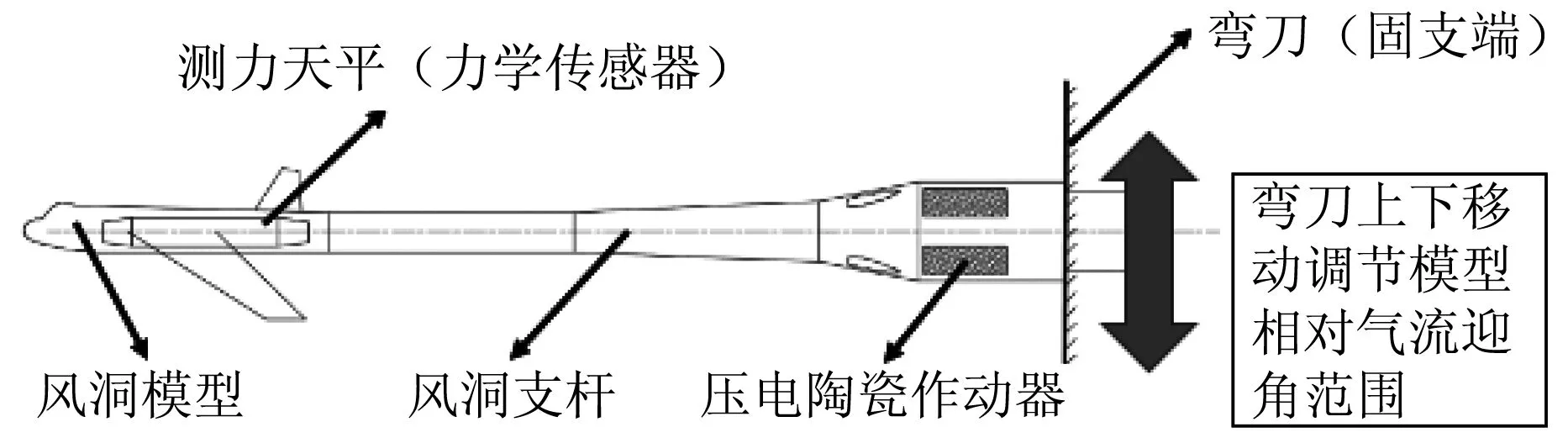
图1 风洞模型—测力天平—风洞支杆悬臂梁系统

1.2 风洞模型振动原因分析

通过对风洞现场的试验观测得知，在大迎角试验中易发生上述振动现象。机翼受力分析图如图2所示，图2中各字母含义为：V是气流速度方向；L是气动力(升力)；D是气动阻力；F是气动合力；v是某时刻模型运动方向。

图2 机翼受力分析图

当飞行器模型处于流场中时，其机翼所受力可分解为与风向同向的阻力和垂直于风向的扬力。在非大迎角试验工况下，由于扬力较大，阻力较小，二者合力几乎与风向垂直。设受到风洞气流扰动的影响，飞机模型机翼在某一时刻向下方运动，即相对于风向斜向右上方运动，此时模型受到的流体作用力也在该方向，即有1个向上的分力，这个分力相当于正的阻尼力，起到衰减振动的作用，此时系统是稳定的[8-9]。

在大迎角工况下，斜向上的相对风向可能产生斜向下的合力，即有1个向下的分力。这个分力相当于负的阻尼力，起到加剧振动的作用，此时系统不稳定，产生自激振动。以上原因导致的自激振动往往是低频(系统的一阶振动模态)、大振幅的振动，该振动能导致系统损坏，严重时会造成风洞设施的破坏[10-11]。

2 基于时滞补偿的振动控制算法

2.1 时滞的产生原因及影响分析

在大迎角试验中，风洞模型产生的自激振动虽然往往是低频振动，但由于风洞气动载荷的激励频带较宽，导致所测得的风洞模型天平支杆悬臂梁系统的振动信号具有大量的高频噪声，且基于测量信号所设计的控制器无法考虑到所有的振动模态，所以在信号处理时，需要通过低通滤波器来去除残余模态和噪声信号。滤波器的使用会引入时滞，这是时滞的重要来源。此外时滞产生的原因还有如下几个方面：1)测量信号的时滞，信号从传感器传输至控制计算机产生的时间延迟；2)计算时滞，控制器根据传感器信号进行控制力的计算时所产生的时间延迟；3)控制信号的时滞，控制信号从计算机传递给作动器的传输时间延迟；4)作动器时滞，作动器产生控制力的过程所用时间。

依据时滞量的大小以及系统选用的控制参数，时滞的影响会不同。时滞的存在通常会影响系统的稳定性，即造成控制系统失稳。有时在保证系统稳定性的情况下，时滞的存在会造成振动控制效果变差，甚至完全没有效果。

2.2 时滞的辨识

通过对风洞模型—测量天平—风洞支杆悬臂梁系统风洞试验的振动信号进行分析，得出振动抑制的主要目标是抑制系统的一阶低频大振幅振动，这也与振动原因分析中模型的自激振动主要为共振频率处的振动相符。本文采用振动控制系统原始振动信号与压电作动器作动信号对比的方法实现输出时滞的辨识。时滞辨识框图如图3所示。

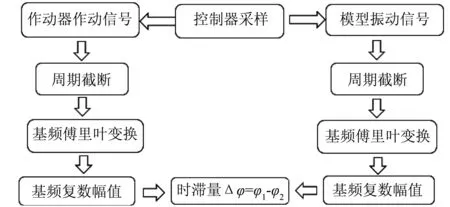
图3 时滞辨识框图

首先对采样后得到的离散时域信号进行离散傅里叶变换。若以a(nΔt)表示离散后的时域信号，n=1,2,…,N(N为采样点数)，离散傅里叶变换公式为：

(1)

对于线性系统而言，固定频率激励输入信号经过时滞通道后的输出信号也为固定频率信号。由于一阶振动信号为低频信号，周期长，时滞量并不超过信号的1个周期，可以将输入输出信号各截断nΔt，即N个采样点数的截断信号进行分析，其基频谱线具有幅值和相位如下：

(2)

(3)

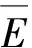
(4)

2.3 系统状态空间求解

2.3.1 未考虑时滞的系统状态空间

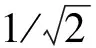
(5)

未考虑输出时滞时风洞模型天平支杆系统的传递函数为：

(6)

式中，ξ是结构的阻尼比；ωn是结构的模态频率，若只考虑一阶振动时，取n=1。

风洞模型—测力天平—风洞支杆悬臂梁系统可近似为连续线性系统，该悬臂梁系统的状态空间方程近似为：

(7)

式中，A、B、C均为实常数矩阵；D为实常数；u为状态反馈的控制力。

由G0(s)得：

(8)

因此，系统的线性微分方程可写为：

(9)

可取状态向量，得：

(10)

则：

(11)

将上式写成状态空间矩阵形式为：

(12)

由上式可得不考虑控制系统时滞时系统状态参数为：

(13)

2.3.2 考虑时滞的系统状态空间

考虑输出时滞时风洞模型天平支杆系统的传递函数：

(14)

由泰勒展开，得：

(15)

省略高次余项，得：

(16)

将式16带入式14，得：

(17)

考虑时滞的系统线微分方程可写为：

(18)

取状态向量，得：

(19)

(20)

即：

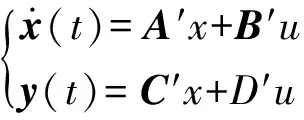
(21)

则考虑控制系统时滞时系统状态参数为：

(22)

2.4 线性二次型调节器振动控制算法

假设K为状态反馈控制器，则：

u(t)=-Kx(t)

(23)

将式10带入式23可得：

(24)

式中，Ac=A-BK。

经状态反馈控制后，控制系统的固有振动特性由矩阵Ac决定，式24的解为：

x(t)=eActx0

(25)

为寻找使闭环系统稳定，形如式10的反馈控制器，设计如下最小化指标函数：

(26)

式中，Q和R为加权矩阵，且Q为半正定对称，R为正定对称。

该指标函数综合考虑了风洞模型—测力天平—风洞支杆悬臂梁系统的振动控制效果和所需要施加的控制力。将式25带入式26，可得：

(27)

则根据最优控制理论所得最优控制器为：

K=R-1BTX

(28)

将式13与式22中未考虑时滞与考虑时滞时的系统状态参数，带入上述线性二次型调节器(Linear Quadratic Regulator,LQR)振动控制方程中，得到未考虑时滞时系统的振动控制参数与考虑时滞时的系统振动控制参数分别为K和K′。

3 系统振动控制地面试验

3.1 试验平台介绍

本文搭建了如图4所示的试验系统。压电陶瓷作动器选用德国PI-P-025.40，上下各2只呈正交分布。压电作动器配套功率放大电源为德国PI-E-472。控制器选用dSPACE公司d1103，可实现MATLAB SIMULINK图形化编程，并自动编译成机器语言写入控制器内存。振动模拟激励源选用江苏联能JZK-50振动发生系统。由于支杆弯曲角度很难用于实际振动的测量，且它既是一个空间的变量，又是一个时间的变量，很难直接用于动力学方程的求解，本试验中选用风洞模型的加速度变量做反馈，振动测量装置选用PCB-325C22型加速度传感器。

图4 地面试验系统实物图

3.2 时滞补偿控制器设计

结合对风洞模型天平支杆系统进行扫频得到的振动数据，得到该振动系统的二阶传递函数为：

(29)

3.3 试验结果

使用力锤在相同的力、相同的位置的条件下，对风洞模型-测力天平-风洞支杆悬臂梁系统进行锤击试验，结果如图5所示。

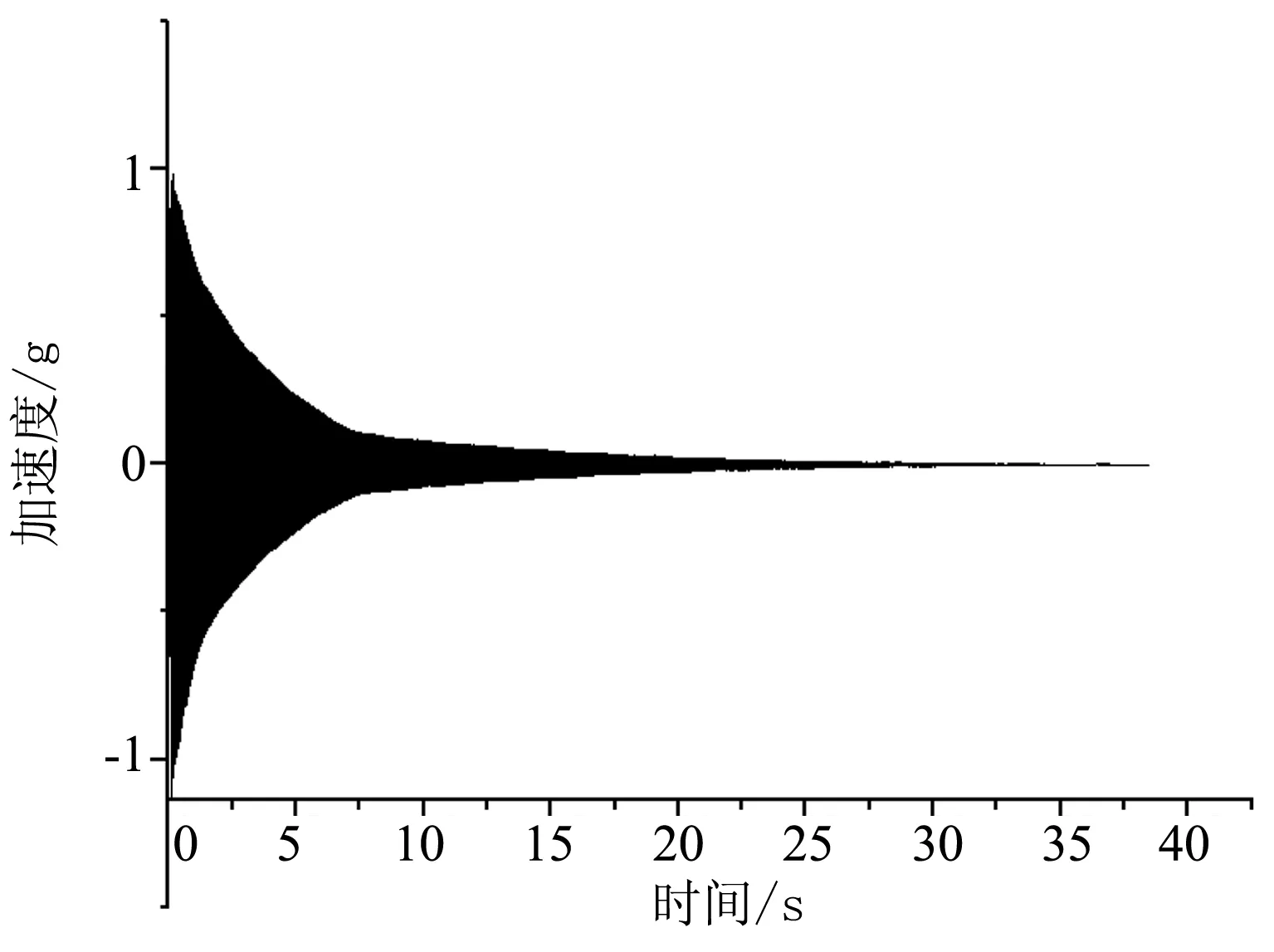
a)未开启振动抑制

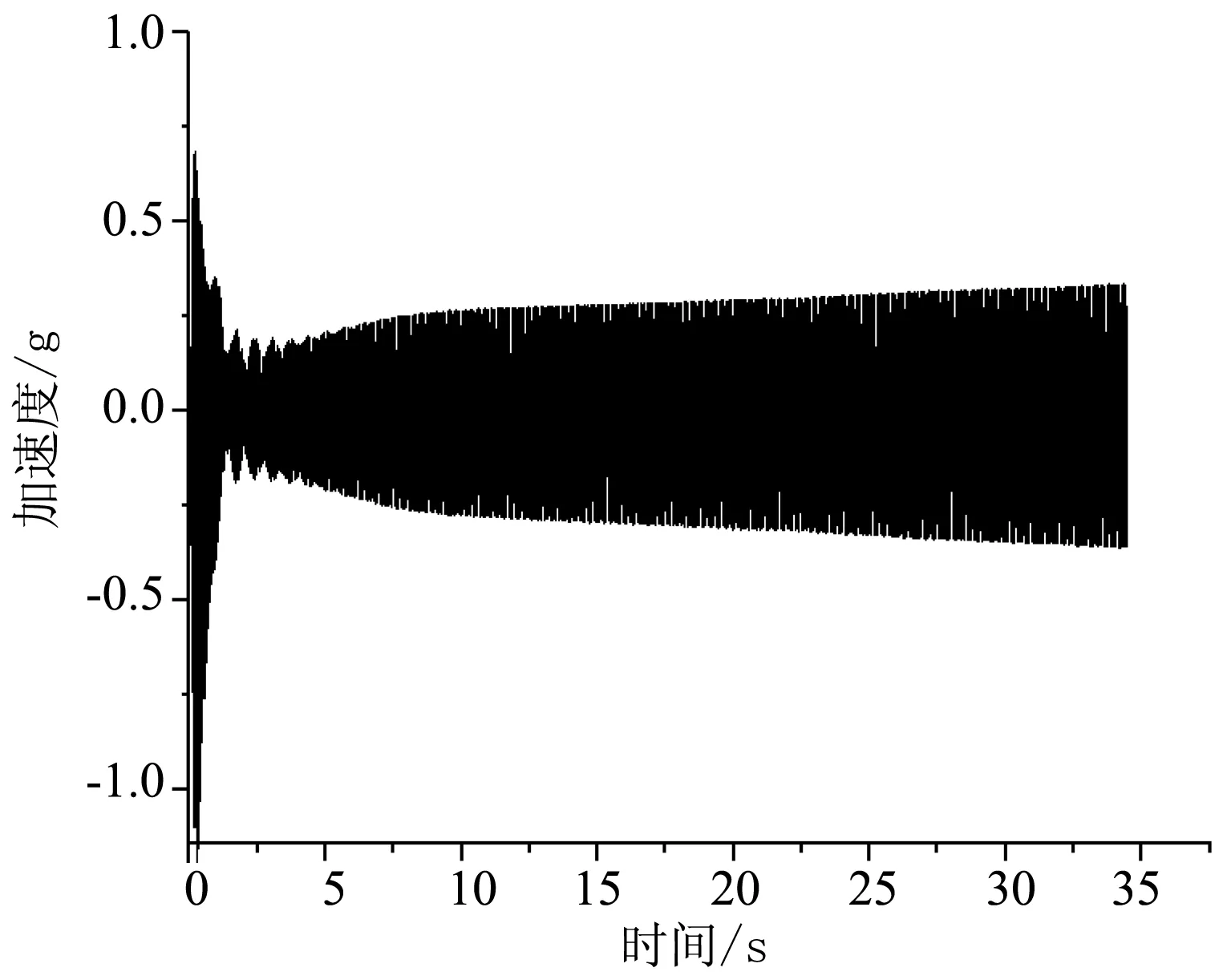
b)未考虑时滞补偿抑振

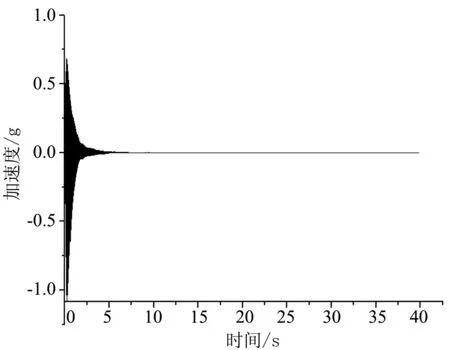
c)考虑时滞补偿抑振图5 锤击试验

在未开启振动抑制时，系统主要在机械阻尼与空气阻尼的作用下振动逐渐衰减回到平衡位置。考虑时滞的振动控制比未开启振动抑制时振动衰减的更加快速，提前20 s左右回到振动加速度为零的平衡位置。以上分析可得开启振动抑制器后系统的阻尼明显增大，说明通过控制压电陶瓷作动器的作动对风洞模型—测量天平—风洞支杆悬臂梁系统起到了主动阻尼的作用。通过对未开启振动抑制与考虑时滞的振动抑制加速度信号进行RMS频谱分析，结果如图6所示，由图6可见，固有频率处振幅衰减了35%。未考虑时滞的振动控制情况下，由于传感器振动信号与作动器作动信号存在相位差，使得作动器在系统中起到了部分负阻尼的作用，振动首先被抑制，然后又趋于发散，最终作动器产生的振动与系统本身的阻尼达到平衡时产生的现象，导致锤击试验时振动控制失效。

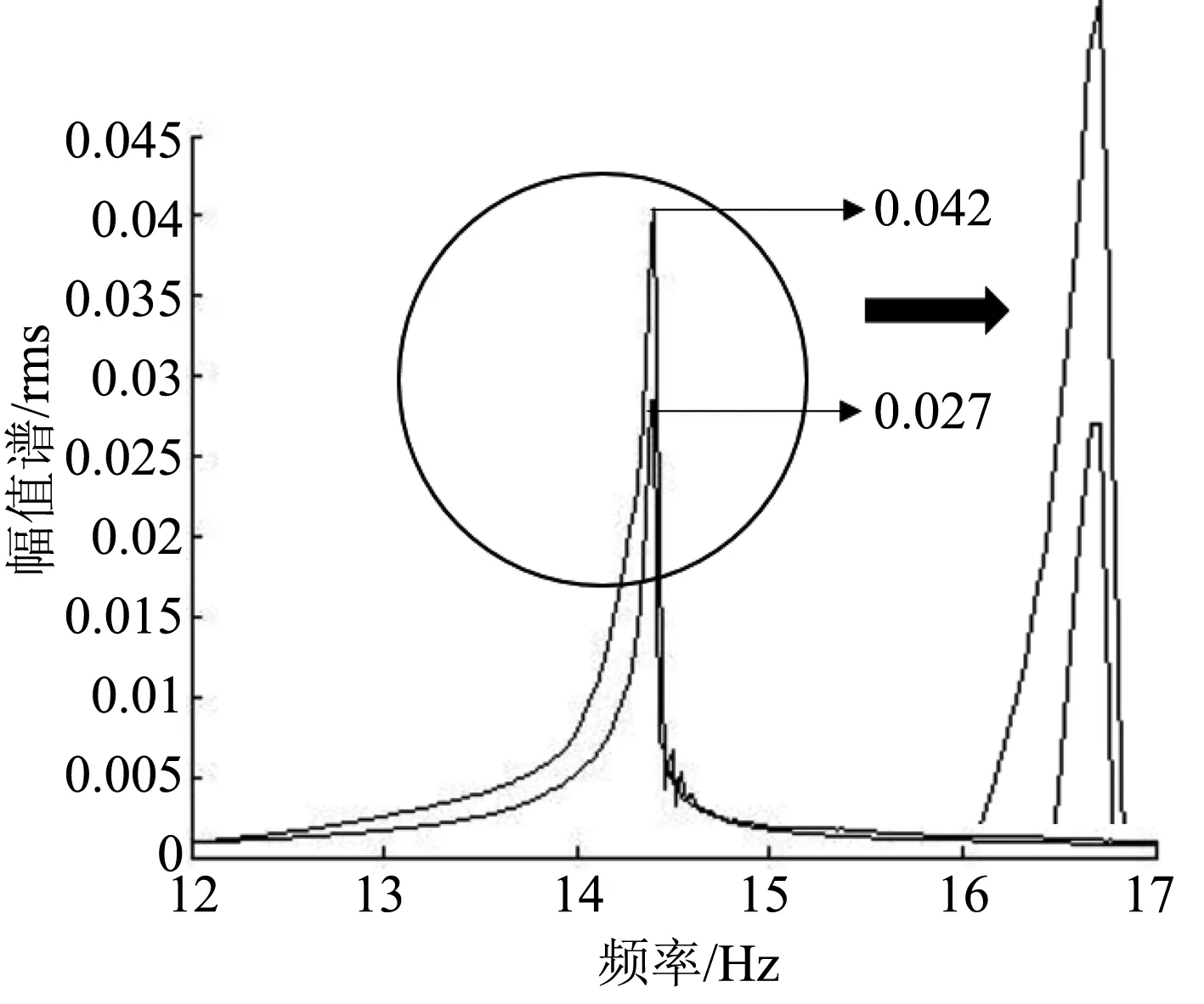
图6 未抑振与考虑时滞抑振频谱对比分析

4 结语

本文针对风洞模型振动控制中的时滞问题，分析了时滞的主要原因为滤波器滤波过程产生了时间延迟。利用基于振动信号与作动器信号的基频傅里叶变换方法实现了风洞模型—测力天平—风洞支杆悬臂梁系统基频处的时滞量辨识。依据半功率带宽法得出系统的二阶模型，并根据此模型设计了基于辨识出的时滞量进行时滞补偿的LQR控制算法。通过锤击试验进行验证得到，时滞的存在导致系统的振动抑制失效，考虑时滞补偿的LQR控制算法相比未考虑时滞的LQR控制算法能够更加稳定有效地对振动进行抑制，具有更好的控制效果。