“多彩、互动、高效”微专题教学——以“有关组合数的求和问题”为例探究

江苏省徐州市第一中学 (邮编：221000)

1 问题的背景

江苏高考卷在2016年，2017年附加题23题都考查了有关组合数的求和问题，借助该题型考查学生综合运用所学基本知识，基本方法，分析问题和解决问题的能力.从考的情况看，学生掌握得很不好，得分率很低.这类题型在平时质检卷23题的位置直接出现和与计数原理问题等综合出现的概率高达二分之一以上.学生反应，看到这类题，就懵，感觉无从下手.

笔者将高二阶段、高三一轮复习阶段的练习题和考试题进行仔细筛选，重新组织，设计了一节二轮复习微专题——“有关组合数的求和问题”.由高考题导入，采用题组呈现、一题多解、一题多变、问题串、小组讨论等丰富多彩的方式，让学生们多思考、多动手、多讨论、多总结.在知识和方法上，努力让学生达到融汇贯通、举一反三的程度；在核心素养上，努力提升学生的逻辑推理、数学运算的核心素养.

2 课堂引入

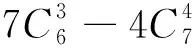
教师：这道题是前一天的作业，第一问都会，第二问同学的做法大多是数学归纳法，方法同标准答案，不同的是在证明n=k+1时的情况处理上，大家采用的是分析法书写(要证……,只要证……)，由要证的结果倒推，想法自然，运算难度降低不少.

教师：还有没有其他做法？第二问的每一项结构有什么特点，上标，下标，前面的系数？第一问有什么作用？

教师：大家动手试一试.

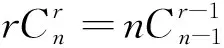
右边.

设计意图由2016年江苏高考题23题引入，引起学生对该类题的重视，方法上也复习了数学归纳法和组合数的常用性质和结论.然后以课本书后习题作为巩固练习，一方面是检测学生对刚刚讲过的高考题第二问思路二的掌握程度，并加深印象.一方面也因为这是道母题，经常是复杂组合数求和的关键步，也是学生容易卡住的地方.最后自然而然地进入了该节课的探究中：还有哪些常考类型？还有哪些常用方法？

3 例题讲解

题型一逆用二项式定理求和

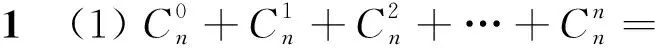
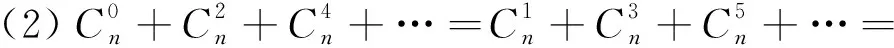
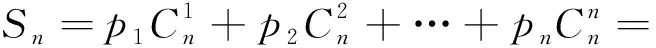
教师：(1)(2)两题是二项式系数很重要的性质，大家一定要熟练记忆.2018年徐州二模的23题，求和关键就是(1)(2)两题的变式，见变式1—4.变式5出处是平时练习中学生没吃透的题.

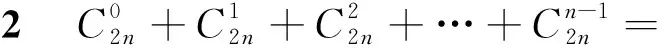
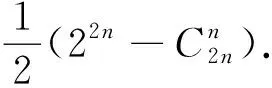
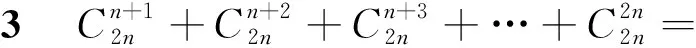
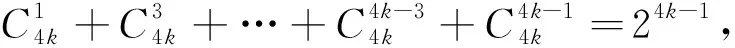
教师：大家小组讨论，这道求和题通项形式是什么？二项式定理可以解决哪类组合数求和问题？并举一些例子.

注问题变式1、3、4答案分别为：

题型二“各项下标相同，上标不同”问题

生二:由组合数的对称性，结合等差数列的求和方法——倒序相加法，可得.

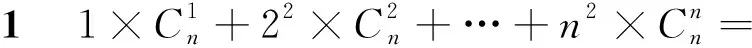
教师：将系数变为平方形式，如何求和？

生二:联想问题3的构造法，在求导之后式子两边乘以x后，两边再求导，再两边令x=1,可得.

教师：完全正确，将未知的问题划归为已知的问题，大家逻辑推理和数学运算能力很不错.如果将系数变为立方形式，是不是可以类似可得？

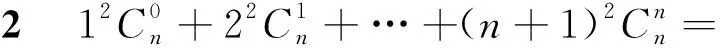
教师：这题是2018年南京一模的23题，结合变式1的做法，谁能说说思路？

下面结合问题3的构造法和变式1的构造法可得.

教师：很好，请大家课后将该题做在作业本上.

注答案为(n2+5n+4)·2n-2.

题型三“各项上标相同，下标不同”问题

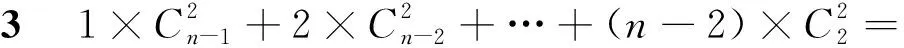
生一：利用

得

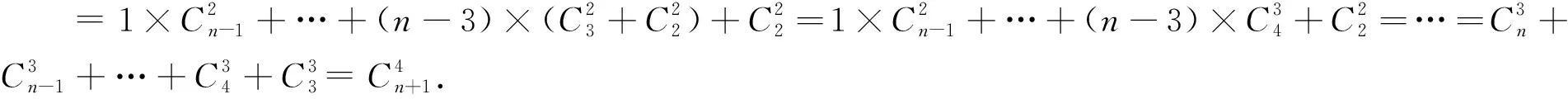
生三:构造，算两次思想

构造(x+1)n-1+2(x+1)n-2+…+(n-2)(x+1)2,

所求即为上式中x2的系数.再由错位相减求和得上式

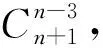
教师：例3与2016年江苏卷所考一题类型一致，各项上标相同，下标不同.两类题的解决都有多种方法，大家课后认真消化.

题型四各项是组合数相乘的形式

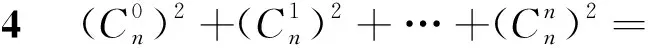
学生：构造，算两次思想

为所求的式子.

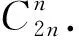
教师：该题是苏教版选修2-1课本43页17题阅读题，主要介绍算两次的方法.计数原理法出自于课本二项式定理的证明方法，学生没有想起来，但方法很简洁，漂亮.要了解.

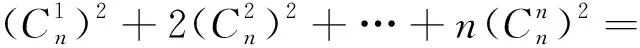
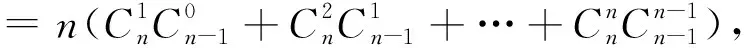
生二:联想问题3的倒序相加法，可得所求.

题型五各项出现了(-1)n

简析构造，算两次思想

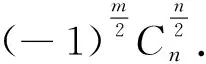
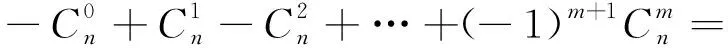
简析裂项求和法.因为当r=1,2,…时，

4 教后反思

这堂课所有题学生都做过，但分布在各张试卷上，知识和方法都非常零散，不便于比较，消化，吸收.微专题教学的设计就很好地弥补了这个问题.具体操作：引入和例题是前一天发给学生，要求做完.上课时让学生们展示他们各种各样的方法，然后通过问题串、变式题将他们的思维进一步深化和整合.目的是下次碰到类似题能够较快地找到优美解法，解决问题.

但真正上课才发现，虽然这些题学生都做过，但变式题学生做的并没有想象中好，我认为老师讲远没有学生自己思考出来收获大，所以我有意识把速度放慢，多给学生“想一想，做一做，议一议”的时间.一节课的内容，我拆成了一节半课讲完，第二节课最后半节课留给学生自主整理、谈论和答疑.课后和部分学生进行沟通，学生反映这节课收获颇多，对这类题常见类型和方法也有了较深刻的理解，大部分的题也基本没问题.但是课后还要定期通过复习和做题去巩固提升.

高三中后期，将重要考点和频繁考点通过微专题的形式呈现给学生，在不断提升了学生对中档题和难题的掌握程度的同时，也不断提升了学生数学核心素养.但要关注一个“慢”字.在“慢”中老师要耐心倾听、平等对话、追根溯源，让学生充分思考、充分表达、充分消化，这样才能收获幸福、收获精彩、收获奇迹！