基于双重配准的机器人双目视觉三维拼接方法研究*

艾青林，刘 赛，沈智慧

(浙江工业大学 机械工程学院，浙江 杭州 310014)

0 引 言

机器人视觉导航是移动机器人研究的重要方向。由于视觉传感器相互间不易产生干扰，获取图像信息的速度非常快，而且它是被动接受信号，不易被发现[1]，因而业界对基于立体视觉的障碍物研究越来越广泛。近年来，对立体视觉的研究主要从4个方面进行[2]：图像的边缘信息、颜色信息、光流场的变化和立体视觉。

(1)图像边缘背景复杂、信息量大，但容易受到噪声影响[3]；(2)基于颜色信息的障碍物检测适用于结构化道路，但机器人的工作环境复杂，一些水渍、物体的阴影可能被理解成障碍物，造成误检[4-5]；(3)基于光流的障碍物检测在检测动态障碍物上有优势，但是其计算量大、耗时长[6]；(4)立体视觉从多个图像中提取出目标物体的三维信息，相互匹配获取图像和深度信息，但计算量大，无法满足检测的实时性要求[7]。

近年来，随着芯片性能的提高，基于三维拼接的方法获取更大视角图像方法受到普遍关注[8]。

机器人在外部复杂环境中，受摄像头视角限制，很难获取障碍物的完整信息，针对这个问题，本文将轮廓识别和立体视觉方法相结合，基于双重配准算法对双目立体视角下两幅重建的三维点云进行拼接，以消除噪声等环境因素影响，快速准确得到障碍物信息；同时，根据具体要求改变视角范围，实现大视角障碍物检测。

1 基于轮廓识别的三维重建

作为双目视觉的重点[9]，立体匹配的好坏直接影响三维重建的结果[10]。然而，通常情况下，提高立体匹配精度会增加算法的计算量，从而影响机器人障碍物检测的实时性。针对这些问题，本文提出了基于轮廓识别的立体匹配方法，并在此基础上进行快速三维重建。

1.1 基于窗口的灰度匹配原理

灰度匹配原则假设图像中的物体都是纯漫反射的[11]，而且不考虑物体间的相互反射造成的光影变化，这样的假设在短基线的图像对中可以成立。灰度匹配原则降低了问题的复杂性，减少了匹配计算量。

若要计算两个图像点p1=(x1y11)T和p2=(x2y21)T的匹配度，为了提高匹配的准确率，以这两个图像点为中心的n×n窗口匹配。

3×3灰度窗口的向量表示如图1所示。

图1 3×3灰度窗口的向量表示

以图1所示的中点p1为例，将点p1所在3×3窗口中所有像素点的灰度值按顺序构成向量v1。同理，对点p2也做相应处理，得到向量v2。若向量v1和v2的夹角越小，则认为两个点的匹配度越高；反之，匹配度越低。

两个向量之间的余弦值为：

(1)

式中：θ—两向量之间的夹角。

当cosθ=0时，两向量具有最佳匹配；若cosθ=0，则两向量的匹配度最低，通过多次试验得出，取阈值cosθ≥0.9时，两幅图像具有较高的匹配效果。

1.2 基于轮廓识别的立体匹配及三维重建

基于轮廓识别的立体匹配算法：首先对图像中障碍物的轮廓进行检测和匹配，然后采用基于窗口的灰度匹配原则，对匹配轮廓上的每个像素点进行匹配，从而减小搜索范围，提高效率和准确率。

基于轮廓识别的三维重建流程图如图2所示。

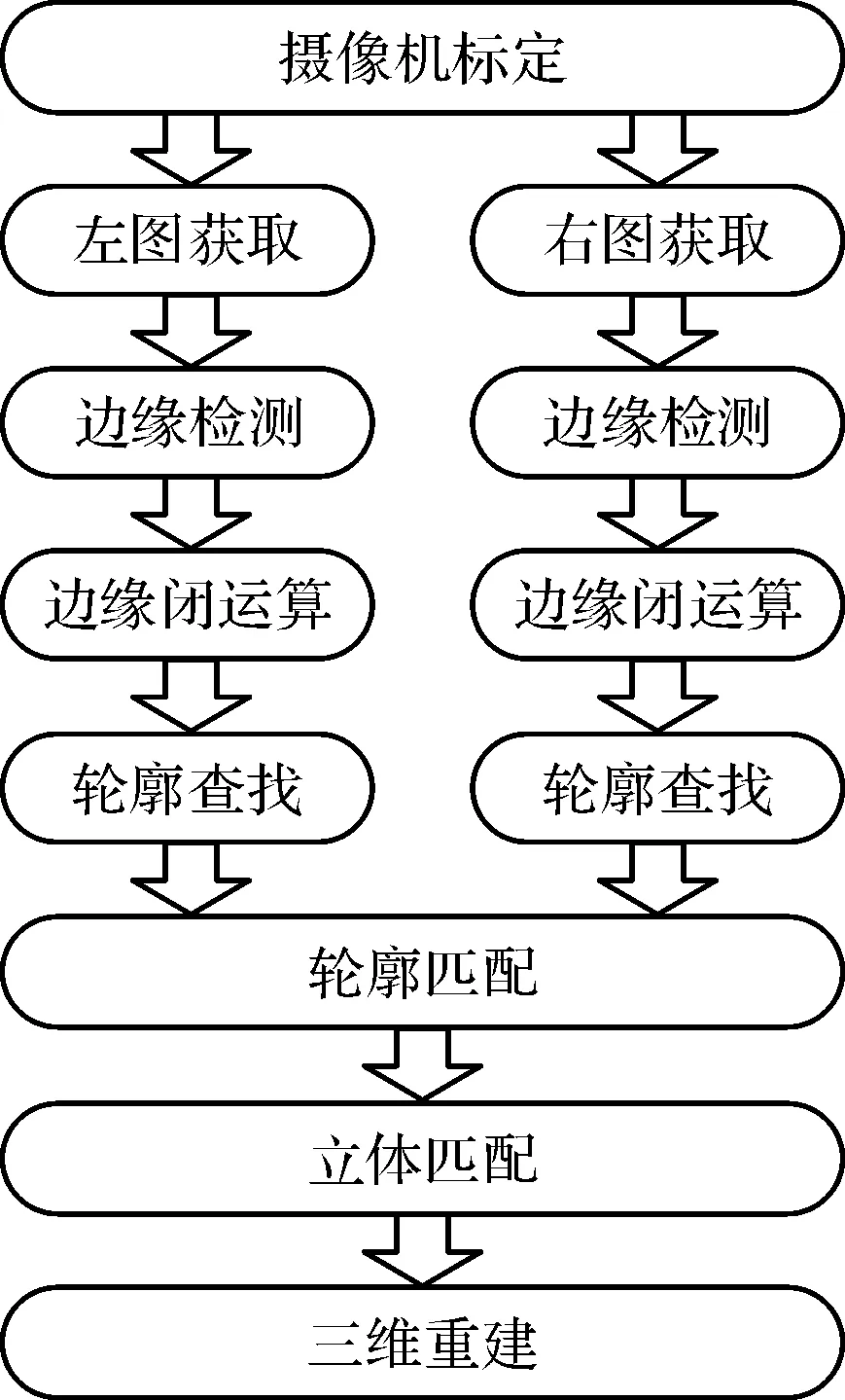
图2 基于轮廓识别的三维重建流程图

由图2可知，基于轮廓识别的立体匹配及三维重建算法分为8个步骤：

(1)摄像机标定。基于张正友标定法利用Matlab对双目视觉系统进行标定，获取摄像机的内外参数，得到更加准确的成像模型；

(2)原始图像获取。原始图像的获取是三维重建的前提，系统通过2台保持一定基距的摄像机获取目标物体的原始图像；

(3)边缘检测。为了在精确定位和抑制噪声之间保持一定的平衡，采用Canny算子对平滑滤波后的左右两幅图像边缘点进行检测；

(4)边界跟踪。通过闭运算连接轮廓上的细小的缺口、裂缝，得到物体完整的边缘。本文中采用5×5的方形核进行闭运算；

(5)轮廓查找。通过查找目标物体轮廓并计算轮廓长度，舍去小于阈值的轮廓，降低立体匹配的计算量；

(6)轮廓匹配。对左右两幅图像中物体的轮廓进行匹配，寻找对应的物体轮廓；

(7)立体匹配。对匹配轮廓上的每个像素点进行立体匹配，匹配值大于阈值的一对像素点视为匹配点；

(8)三维重建。根据摄像机标定的内外参数并结合匹配点计算目标障碍物轮廓的三维信息。

2 基于双重配准的可变视角三维拼接

一般情况下，双目立体视觉得到三维信息的范围是固定的，因此无法得到大视角范围内障碍物的整体三维信息。本文提出了一种基于双重配准的可变视角三维拼接方法，通过4个步骤实现。

2.1 寻找两点云的重叠区域

寻找重叠区域是图像拼接的前提，准确而快速地找到重叠区域则是其重点[12-13]。根据轮廓Hu的不变性，本文提出对用于三维重建的两组图像中左图像Pl1，Pl2进行轮廓匹配，然后寻找匹配轮廓对应的三维轮廓点云，即两点云的初始重叠区域。

为了预先去除因噪声和误匹配造成的异常点，本文通过计算每个目标物体的轮廓对应的三维点云中相邻两点之间的平均距离L，以平均距离的两倍为阈值，若存在三维点到任意相邻三维点的距离大于2L，则将其视为噪声点舍去，从而得到优化后的重叠区域。

2.2 初始配准

本研究计算对应的三维轮廓点云的重心，分别以两点云中距离重心最远的点pf，中间的点Pm和最近的点pn为特征点，通过这3个对应的三维点求解出两坐标系之间旋转矩阵、平移矩阵和尺度因子，以双目视觉系统的全局坐标系O1为基准，将两点云转换到同一坐标系下，完成初始配准。

2.3 精确配准

为了能得到更高的配准精度，笔者基于ICP算法对经过初始配准后的轮廓点云数据进行精确配准。本研究用点集{pi}和{xi}来表示点云数据P和X，利用ICP算法[14]，为点集中每一个点匹配到到另一点集中距离最近点并使其距离的平方和最小，从而计算出点云间的转换矩阵。以矢量q=[qR|qT]表示两点之间的转换矩阵，应用到点云P中，计算所有点对的距离平方和：

(2)

为了准确计算f(q)的最小值,先计算点云P和X的重心：

(3)

(4)

两片点云的互协方差矩阵为：

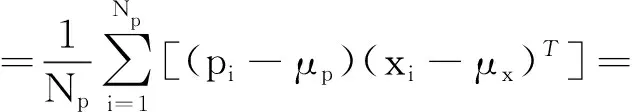
(5)

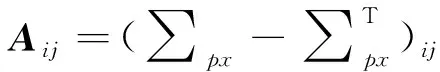
(6)

式中：I3—3×3的恒等矩阵。

由式(6)和qR得到旋转矩阵：

R=

(7)

通过迭代计算得到第一个距离平方和小于给定阈值的点对：

qT=μx-R(qR)μp

(8)

本文通过给点云中不同点赋予不同的权重，剔除其中权重大于给定阈值的点来减少计算量，提高其运行的效率：

(9)

式中：D(p1,p2)—对应点(p1,p2)之间的欧氏距离；Dmax—距离的最大值。

经过处理后，迭代运算中数据量明显减少，极大地提高了ICP算法的效率。

由式(9)可以看出：两点的距离越近，赋给这一对点的权值就越大。

使用改进后的ICP算法对两点集及进行计算。其中：X与P元素数目不一定相同，假设k≥n，根据公式(8)给点云数据点赋予权值，并剔除权值小于阈值的数据点；然后寻找最近点，即为集合X中的每一个数据点，寻找在集合P中距该数据点空间距离最近的数据点，将这些对应点组成的新点集命名为；对点集U与Q配准计算，得到两点集之间的变换矩阵R、T，其中：R—3×3的旋转矩阵，T—3×1的平移矩阵。用配准变换矩阵R、T对集合X进行坐标变换，得到新的点集X1，为X1=RX+T。如果目标函数误差小于阈值，则结束，否则，以U1替换U，重复上述步骤。

2.4 融合

为了得到更好的拼接效果，消除配准后三维点云存在的裂缝等，本文选用加权平均融合算法对拼接后的三维点云进行融合处理[15]。

取加权系数α=0.5，β=0.5，得到加权平均融合算法：

(10)

3 机器人可变视角障碍物检测实验

六足机器人双目视觉实验平台图3所示。

图3 机器人双目视觉实验平台

本文在该平台对三维拼接方法进行验证。其中，六足机器人样机采用CM-700作为下位机主控板驱动关节舵机和外部传感器。机器人每条腿各有3个关节，共18个，全部采用RX-24F舵机驱动，板载传感器包括测距传感器DMS-80以及陀螺仪传感器，机身和腿部采用硬质铝合金构造。所用摄像机为两台U-500C工业相机，YX0612摄像头，其分辨率为2 560×1 920，焦距为6 mm～12 mm。

三维重建在32位Window XP操作系统上以VS2010、VC6和Matlab平台进行编程实现。利用Directshow技术，在VS2010平台上开发双目立体视觉系统的图像采集程序。通过Matlab工具箱对摄像机进行标定，并在VC6平台利用OpenCV和OpenGL开发包完成图像的三维重建和三维拼接。

3.1 基于轮廓识别的三维重建实验

双目视觉系统拍摄的环境障碍物如图4所示。

经过边缘检测并优化后得到的目标障碍物完整轮廓信息如图5所示。

图4 双目立体视觉系统原始图像

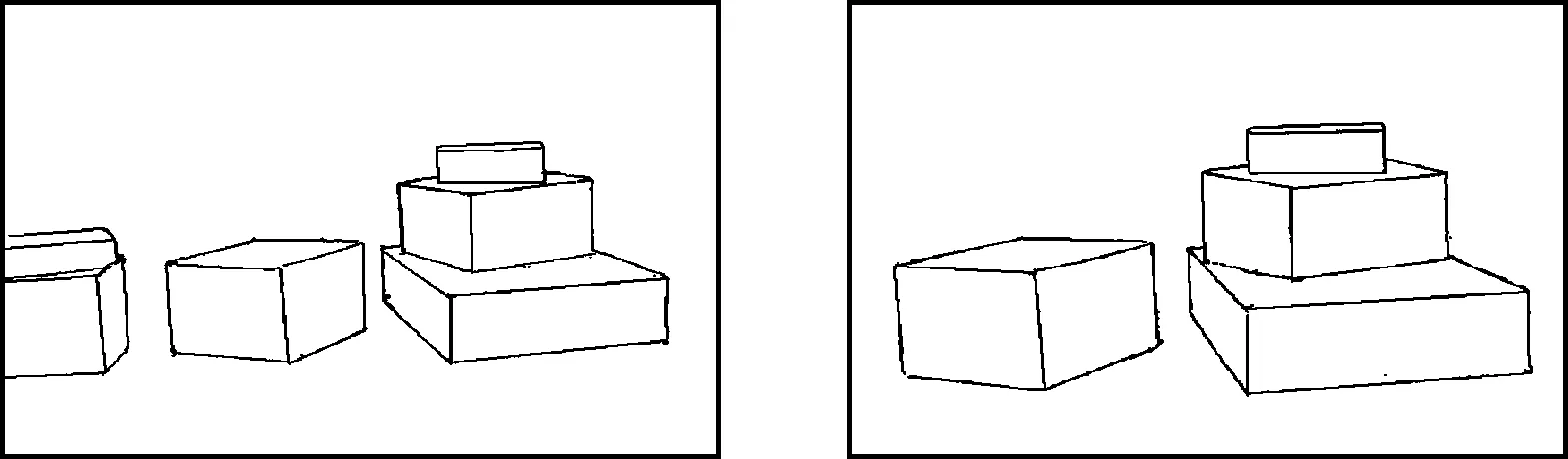
图5 目标物体边缘检测及优化后边缘图像

经过边缘检测以后，图像的像素点减少70%以上，使得后续图像处理的运算速度得到极大提高。从图5中可知：边缘的缺口、裂缝等已经通过边界跟踪被消除了，背景环境中的污渍、阴影等已经通过轮廓查找被舍弃。取阈值cosθ=0.9对图5进行轮廓匹配，生成的三维轮廓点云如图6所示。

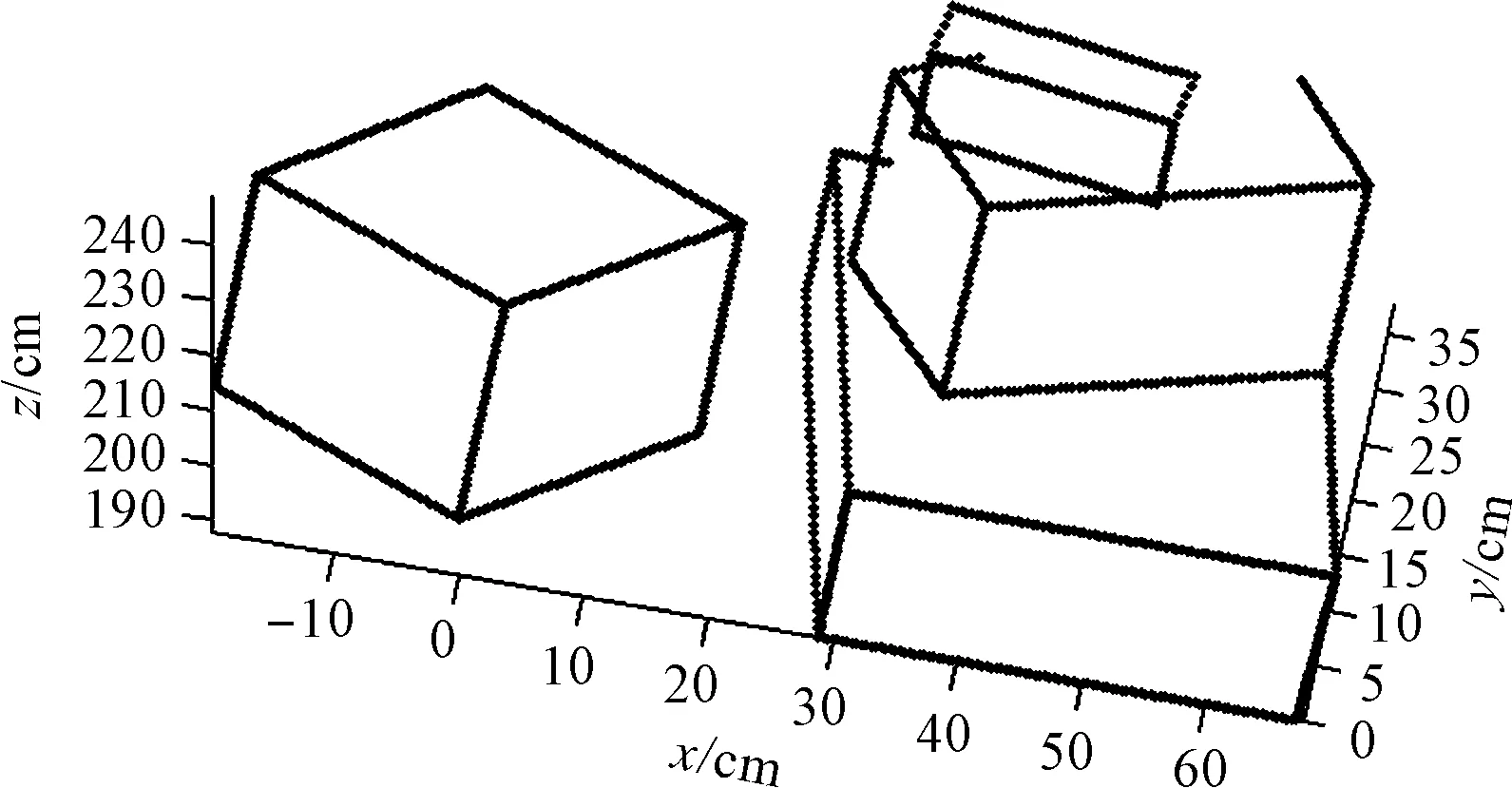
图6 三维重建后生成的轮廓点云

由图6可见：生成的三维重建图像轮廓非常接近实际障碍物模型。

为了定量计算该重建算法的精度，笔者选取重建模型轮廓上的6个角点计算沿不同坐标轴方向的平均重建误差和相对重建误差，各角点实际坐标值与重建坐标值如表1所示。

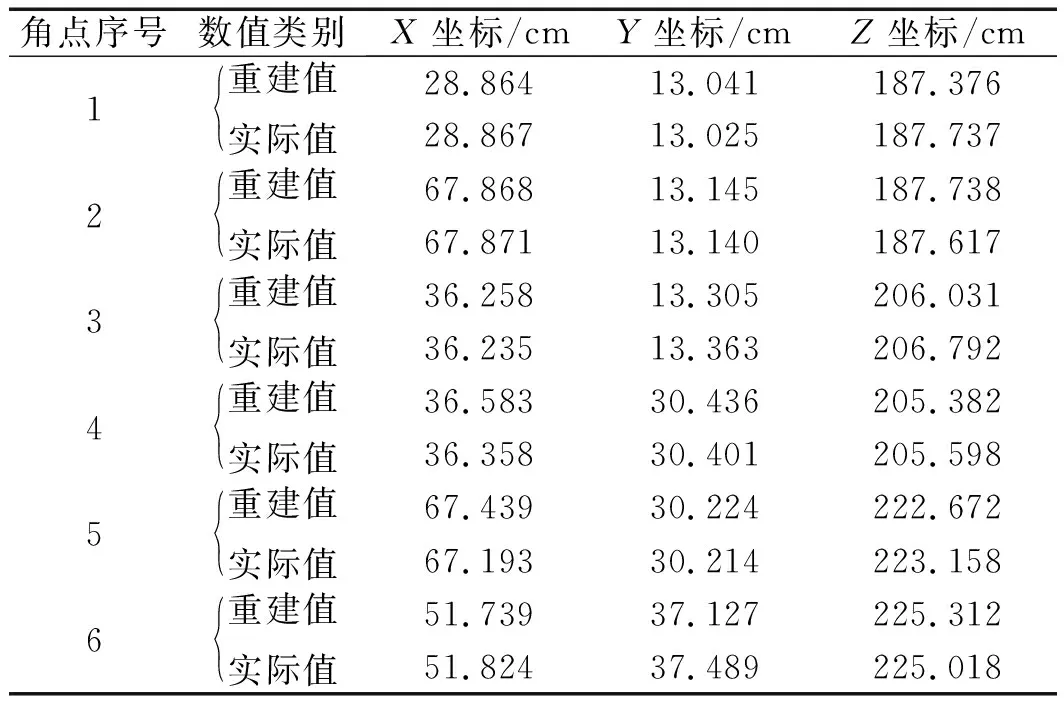
表1 各角点重建坐标值与实际坐标值

本研究通过对实验结果进行测量对比可知：X方向的平均重建误差为0.098 cm，相对重建误差为0.205%；Y方向平均重建误差为0.081 cm，相对重建误差为0.285%；Z方向的平均重建误差为0.369 cm，相对重建误差为0.181%。可知基于轮廓识别的快速三维重建精度较高，能够达到机器人目标障碍物检测的要求。

3.2 基于双重配准的可变视角三维拼接实验

通过双目立体视觉系统对障碍物不同视角进行拍摄得到的4幅原始图像如图7所示。

图7 双目立体视觉系统两次拍摄的原始图像

经过边缘检测及边缘跟踪后得到完整的目标障碍物轮廓信息如图8所示。

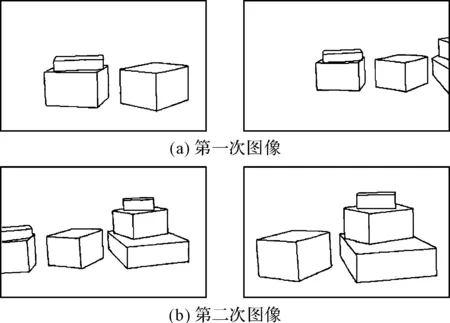
图8 目标物体边缘检测及优化的边缘图像

本研究分别对图8中两次拍摄图像的轮廓信息进行轮廓匹配和三维重建，得到的两组三维重建图像轮廓点云如图9所示。

图9 重建两次拍摄图像的三维点云

本研究通过上述拼接方法对图9的两组三维点云进行拼接和融合，得到三维图像如图10所示。

图10 基于双重配准算法拼接大视野三维点云

由图10可知：通过将两组三维点云在同一坐标系下进行拼接融合以后，机器人进行障碍物检测的视角大大提高。

为了定量计算三维拼接以后生成的图像精度，本研究选取目标物体轮廓上的角点计算拼接误差，各角点实际坐标值与拼接后的坐标值如表2所示。

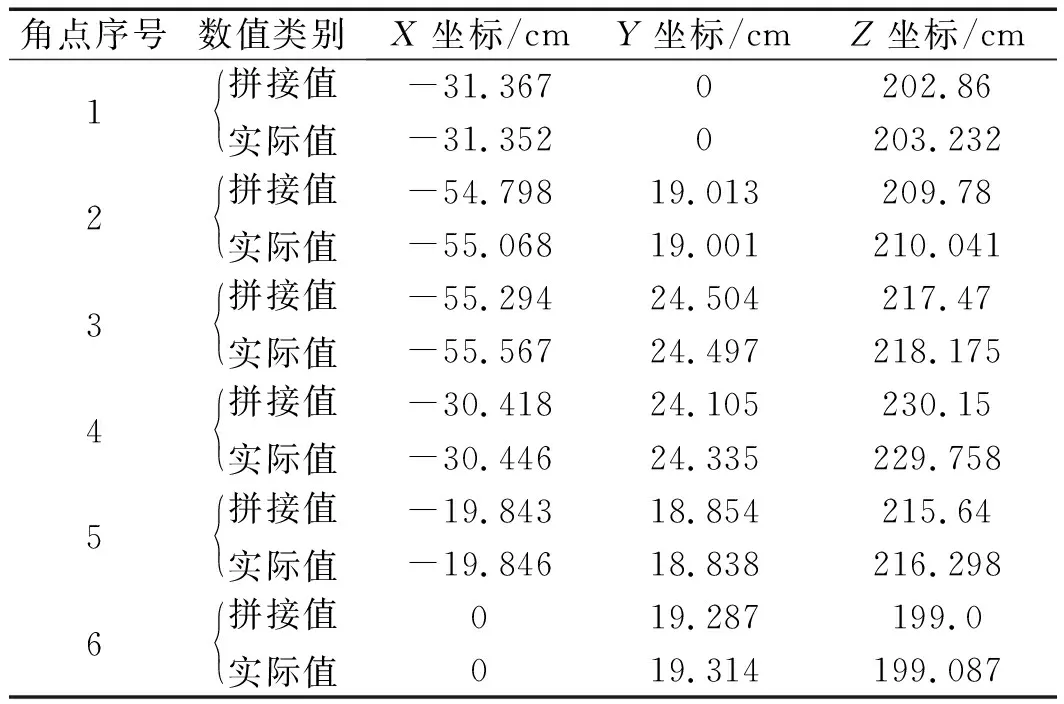
表2 各角点的拼接坐标值与实际坐标值

由对比实验结果可知：X方向的平均重建误差为0.098 cm，相对重建误差为0.189%；Y方向平均重建误差为0.048 cm，相对重建误差为0.210%；Z方向的平均重建误差为0.413 cm，相对重建误差为0.184%。由此可见：基于双重配准算法对两幅三维重建图像进行拼接以后，机器人进行障碍物检测的视角大大提高，且重建误差较低。

4 结束语

针对机器人在外部环境中因视野范围受限，无法准确获取障碍物完整信息这一问题，本文通过可变视角三维拼接方法重建了障碍物三维模型，获取了障碍物更大的视野图像，具体如下：

(1)将基于轮廓识别的边缘检测法与三维重建方法相结合，准确获取了目标障碍物的轮廓信息，消除了多余轮廓，减少了大部分图像像素点，极大地提高了算法的运算速度；

(2)提出了基于双重配准算法的可变视角三维拼接方法，建立了数学模型，通过改变双目立体视角范围获取障碍物的更大视野图像，并根据点云融合算法提高了配准精度；

(3)进行了可变视角三维拼接实验，结果表明：通过可变视角三维拼接方法重建的三维模型具有较高的空间坐标精度，且图像误差较小。