数控机床传动机构精度可靠性优化研究*
徐 琦,罗路平,夏 力
(浙江工业大学 浙江省特种装备制造与先进加工技术重点实验室,浙江 杭州 310014)
0 引 言
数控机床为先进制造行业的基础装备,其加工精度及可靠性决定了我国机床制造业的水平。数控机床实际加工过程中,存在许多类型各异、产生原因复杂的不确定性误差,常常导致数控机床精度低、可靠性差等问题。常见机床误差主要分为几何误差、热误差、切削力误差、运动误差、夹具误差、伺服误差等。其中,当温度变化较稳定时,几何误差是最重要的误差因素之一,约占总误差的40%[1-2],因此在机床研制过程中,优化几何误差能有效提高机床精度可靠性。
近年来,数控机床精度可靠性优化受到了国内学者的广泛关注,如郑财、黄贤振等[3]基于多体系统理论建立的数控机床空间几何误差模型,运用改进的一次二阶矩法和蒙特卡洛法,进行了三轴数控机床空间加工精度可靠性计算;李翠玲[4]、贾丹丹[5]等基于多体系统理论,建立了数控机床的误差模型,结合随机输入误差,进行了机构运动精度可靠性计算;田文杰[6]、刘恩[7]等利用激光干涉仪基于九线法检测,通过几何误差辨识模型,对数控机床运动轴几何误差进行了溯源,为机床精度优化提供了理论指导;韩飞飞[8]借助球杆仪对平面综合误差进行圆检验,分析了工件坐标系下综合误差分量与球杆仪半径变化之间的关系,获得了圆偏差产生的各项因素及所占比例,通过机床硬件调整、修理、更换,快速提高机床的精度性能。
综上所述,目前学者们大多是基于建立的数控机床空间误差模型及仪器测量的方式,确定较简单的数控机床的几何误差值,并未根据数控机床传动机构的结构,进行几何误差的深层溯源确定。
本文以某数控机床传动机构为研究对象,在机床空间误差建模的基础上,根据影响因素误差多层映射模型,得到X、Y、Z轴3个方向上的传动机构主要零部件参数与机床空间几何误差的传递模型;利用一次二阶矩法进行混合几何误差精度可靠度分析,结合可靠度灵敏度分析,实施数控机床传动机构精度可靠性优化,确定机床传动机构几何误差的精度参数。
1 某数控机床几何误差建模
1.1 基于多体系统理论的数控机床几何误差建模
某数控机床为三轴伺服直联控制半闭环立式加工中心。三轴均为钢球滚动直线导轨,采用高精度高强度的内循环双螺母预压大导程滚珠丝杠,且主轴通过同步带驱动伺服电机,其机构简图如图1所示。
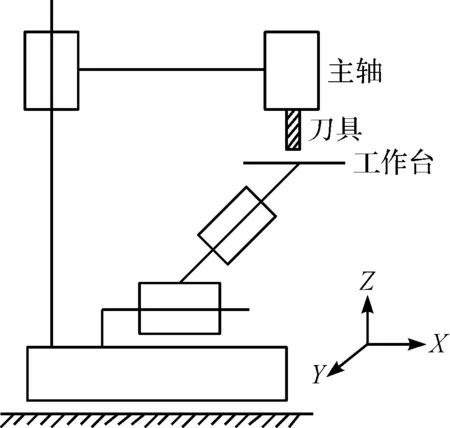
图1 某数控机床机构简图
以数控机床床身为参考体进行标定的拓扑结构图如图2所示。
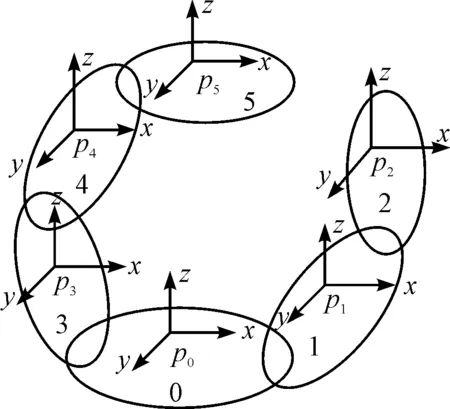
图2 拓扑结构图0—床身;1—X向滑台;2—Y向工作台;3—Z向导轨;4—主轴;5—刀具
结构包括床身—工作台运动链和床身—刀具运动链,在此基础上建立基于多体系统理论的数控机床几何误差模型[9]。
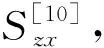
导轨X轴方向的6项误差如图3所示。
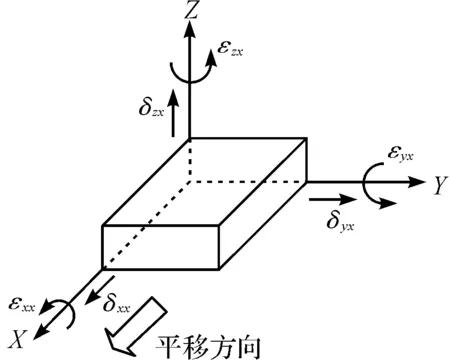
图3 导轨X轴方向的6项误差
由位姿变化矩阵传递法则可知[11],点Ki在相邻低序体G坐标系中的位置坐标可以表示为:
(1)
式中:TSG—高序体S与相邻低序体G之间的位姿变换矩阵;TKS—高序体K与相邻低序体S之间的位姿变换矩阵;PKi—点Ki在体K坐标系中的位置坐标。
因此,数控机床移动轴在经过微小移动和转动后,位姿误差变换矩阵和垂直度误差变换矩阵分别为:
(4)
式中:Δx,Δy,Δz—变换过程中沿X、Y、Z轴的微小移动量。
根据几何误差变化方法,相邻序体间实际(有误差)运动的变换矩阵可表示为:
Tij=TijpΔTijpTijsΔTijs
(6)
式中:Tijp—序体相对静止的理想位置变换矩阵;ΔTijp—序体相对静止的实际位置变换矩阵;Tijs—序体相对运动的理想位置变换矩阵;ΔTijs—序体相对运动的实际位置变换矩阵。
故数控机床的各序体之间的空间位置误差转换矩阵可以表示为:T01=RyzT(x),T12=RxyT(y),T03=RzxT(z),T34=I4×4,T45=I4×4。
设刀具上的成型点在刀具坐标系中的齐次坐标为Pt=(ptx,pty,ptz,1)T,在工件坐标系内理论位置变化曲线为Pw=(pwx,pwy,pwz,1)T,因此数控机床空间位置误差可是表示如下:
E=T01T12Pw-T03T34T45Pt=(Ex,Ey,Ez,1)T
(7)
式中:Ex,Ey,Ez—数控机床X、Y和Z轴3个方向位置误差。
1.2 数控机床传动机构几何误差建模
本研究根据数控机床误差传递结构,建立能直观反映数控机床零部件与数控机床末端位姿精度耦合和递进影响关系的影响因素多层映射模型图,如图4所示。
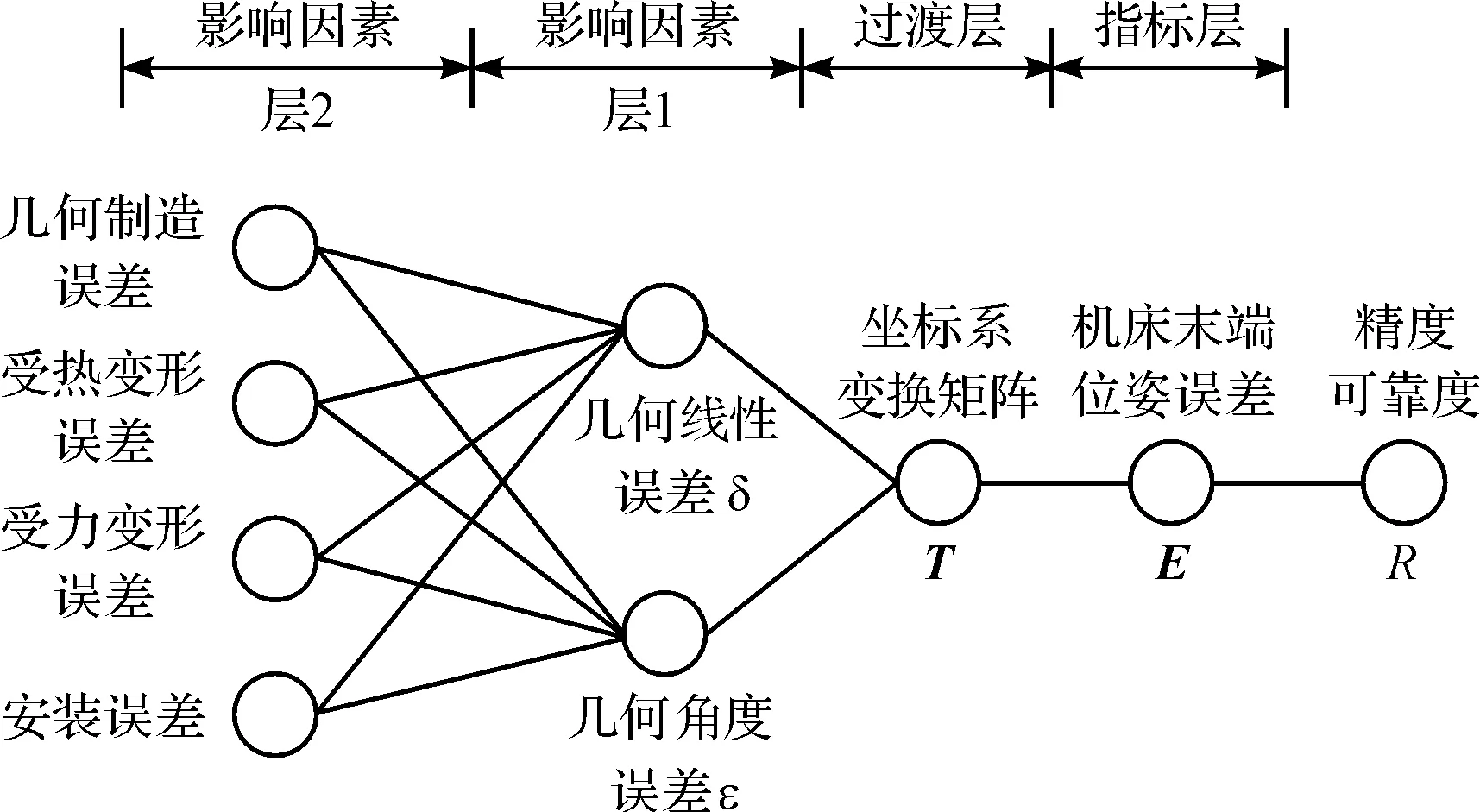
图4 数控机床传动机构精度可靠性影响因素多层映射模型
本研究根据该模型图确定数控机床传动机构主要零部件参数与数控机床空间几何误差项的传递关系,建立更为具体、精确的数控机床传动机构的空间几何误差传递模型,为精度可靠性优化打下基础。
针对影响因素层1和2,将数控机床传动机构简化为控制电机—齿轮减速机构—滚珠丝杠—工作台/刀具,数控机床传动机构结构示意图如图5所示。
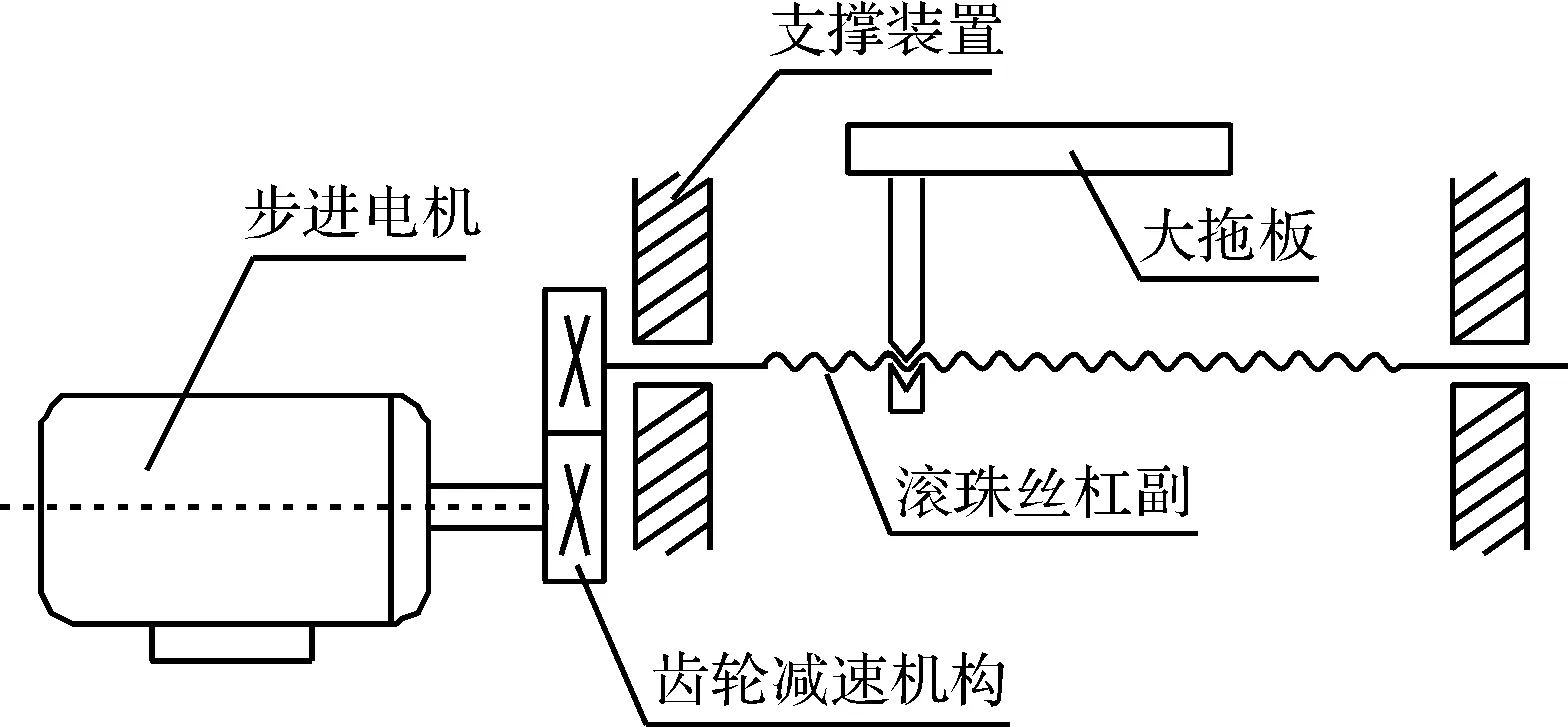
图5 数控机床传动机构结构示意图
由图可知:滚珠丝杠的几何误差将最直接影响工作台或者刀具的几何误差。为了适当简化分析模型,本研究通过对X、Y、Z轴3个方向上的滚珠丝杠副进行具体分析,确定滚珠丝杠几何误差与数控机床21项几何误差的对应关系。
以X轴朝向的滚珠丝杠为例进行分析,根据国家标准和现有研究可得如下公式:
(8)
(9)
(10)
(11)
(12)

已知数控机床传动机构的滚珠丝杠几何参数如表1所示。
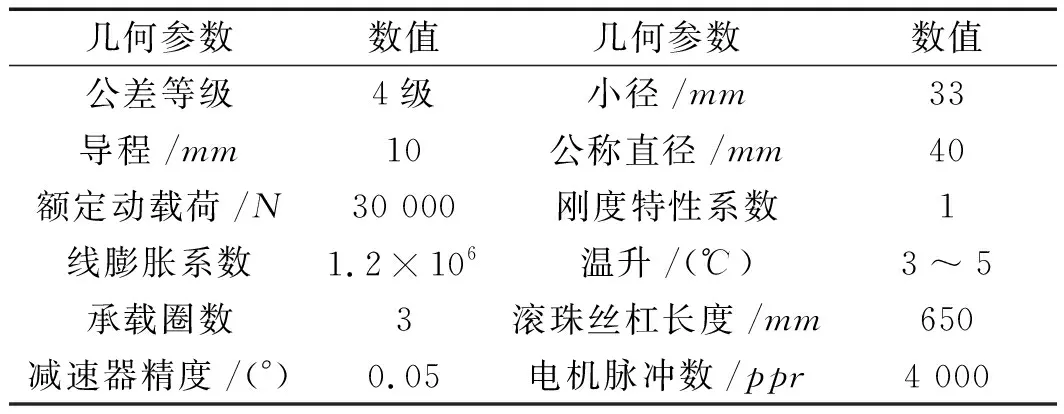
表1 滚珠丝杠几何参数
根据式(8~12)中各误差参数计算公式可得数控机床X轴误差参数分布情况,如表2所示。

表2 误差参数分布(直线误差:μm,角度误差:弧秒)
将表2中各误差参数代入式(8~12),确定数控机床X轴传动机构的几何误差分布情况,同理可得数控机床Y轴和Z轴传动机构的几何误差及对应的垂直度误差。
数控机床传动机构21项几何误差参数及编号如表3所示。

表3 数控机床传动机构21项几何误差参数及编号(直线误差:μm,角度误差:弧秒)
将表3数值代入公式(7)可得到数控机床在X、Y、Z轴3个方向的总误差Ex、Ey和Ez。
2 数控机床传动机构精度可靠性分析
2.1 传动机构几何误差精度极限状态函数
设I为数控机床传动机构的最大几何误差,则数控机床传动机构几何误差精度可靠性极限状态函数为:
(13)
式中:*—误差方向(“+”—沿运动方向;“-”—沿运动反方向),同方向误差值进行判断;i=x,y,z;X—随机变量向量;Y—区间变量向量。
由式(7)可知:当数控机床位置坐标x、y、z,刀具成型点坐标Pt和Pw已知时,极限状态函数G中变量为:
X=(δy(x),δz(x),εy(x),εz(x),δx(y),δz(y),εx(y),
εz(y),δx(z),δy(z),εx(z),εy(z),Sxy,Syz,Szx)
Y=(δx(x),εx(x),δy(y),εy(y),δz(z),εz(z))
2.2 基于一次二阶矩的混合几何误差精度可靠性计算
数控机床传动机构精度性能可以通过极限状态函数值是否大于0来决定,当G<0时,系统失效,故失效概率可表示为:
(14)
式中:Pr{·}—概率。
可靠度可表示为:
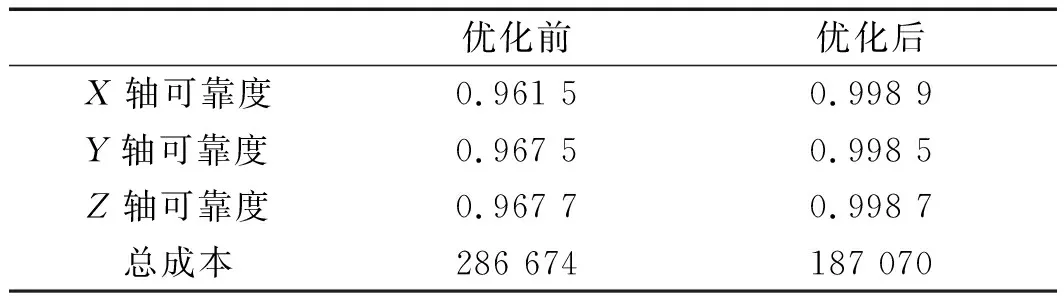
R=Pr{I- (15) 由于区间变量Y的存在,数控机床传动机构的误差Ei在空间中是由两个极限边界面组成的极限状态带,根据条件概率公式,可得失效概率的最大值和最小值: (16) 根据一次二阶矩法,失效概率的最值计算公式又可以采用文献[17]的方法进行计算,即: (17) 式中:u*—最大概率点。 某数控机床传动机构在未经过伺服系统控制状态下的精度要求:X、Y、Z轴定位精度为0.1 mm,以此为条件,可求得该数控机床传动机构精度可靠度,如表4所示。 表4 数控机床传动机构精度可靠度 由表可知:数控机床传动机构在不同移动方向上的精度可靠性均值为96.89%,最小值为95.21%,精度可靠性较低,需要对各误差进行合理控制。 由于所有误差的分布类型、分布参数都将对可靠性的灵敏程度产生影响,本研究通过可靠性灵敏度分析确定各误差的分布参数灵敏度程度。 本文主要通过数控机床传动机构在X、Y、Z轴3个方向上的总误差Ei对各个误差Δej={δk,εl,Sm}求偏导,得到数控机床传动机构各几何误差的灵敏度[18]: (18) 对灵敏度进行归一化处理,得到对应灵敏度系数: (19) 由式(7,18~19),可求得21项几何误差的灵敏度系数,如图(6~8)所示。 图6 X轴方向误差源灵敏度系数 图7 Y轴方向误差源灵敏度系数 图8 Z轴方向误差源灵敏度系数 由图(6~8)可以看出:X轴和Z轴方向上,εy(x)、εy(y)、εy(z)、Szx的灵敏度较高,Y轴方向上,εz(x)、εz(y)、εz(z)、Sxy的灵敏度较高。 误差源编号如表3所示。并将灵敏度系数较小的误差源合并,编号为22。 基于可靠性灵敏度分析结果,本研究对数控机床传动机构21项几何误差的精度分配进行优化设计。 3.2.1 精度优化模型 本研究以制造成本最小化为优化目标,建立数控机床传动机构几何误差的精度分配的优化模型[19]: (20) 式中:xi—各项几何误差值;ki—各变量的成本权重系数。 在设计制造阶段,不能精确给出数值,因此笔者对其进行定性估计,本研究以3个方向上最大灵敏度为成本系数,进行归一化处理,得到相应的成本权重系数[20-22];λi—线位移和角位移量纲同一化系数,线位移量纲为λi=1,角位移量纲为λi=57.2[23];αi—公差特征指数,取αi=2。 设计变量即为各项几何误差项,可表示为: x=(δx(x),δy(x),δz(x),εx(x),εy(x),εz(x),δx(y), (δy(y),δz(y),εx(y),εy(y),εzy),δx(z),δy(z), δz(z),εx(z),εy(z),εz(z),Sxy,Syz,Szx) 根据数控机床传动机构精度要求,X、Y、Z轴传动方向上的误差约束条件可表示为: (21) 根据各项误差源的分布情况,单个误差源的约束条件可表示为: ximin≤xi≤ximax (22) 3.2.2 精度可靠性优化结果对比 数控机床传动机构几何误差分配优化的目的是在满足约束条件下寻找制造成本的最优解。本研究基于Matlab编程,采用遗传算法进行误差分配优化,配置参数:初始种群数为200,随机均匀分布,按0-1二进制杂交,杂交概率为0.8,双向迁移,运行100代停止,运行求解;采用蒙特卡洛抽样法求解每组精度分配值的精度可靠性。 分配优化结果如表5所示。 表5 数控机床传动机构21项几何误差分配优化结果(直线误差:μm,角度误差:弧秒) 精度优化结果如表6所示。 表6 数控机床传动机构精度优化结果 对比表(3,5)可知:各误差变量取值与初始误差均值存在偏离值,且灵敏度系数较大的误差偏离值相对更大,而灵敏度系数较小的误差偏离值相对较小。在满足精度要求的前提下,合理选择较大的误差参数,能更大程度地降低制造成本。 由表6可知:优化后,数控机床传动机构的精度可靠度平均值为99.87%,最小为99.85%,精度可靠度得到提高,成本从优化前的286 674降低到187 070,降低34.74%。由此可见,该方法能在满足精度可靠性的条件下有效地降低了制造成本,为设计制造过程中零部件精度选择提供了依据。 针对数控机床误差溯源不充分导致精度低、可靠性差等问题,本研究对数控机床误差建模、精度可靠性分析、精度优化设计等方面进行了研究,具体为: (1)建立了数控机床几何误差模型,根据误差传递结构,建立了数控机床传动机构的几何误差传递模型和影响因素多层映射模型图,为数控机床传动机构精度可靠性分析和优化打下基础; (2)结合数控机床传动机构精度可靠度影响因素的不确定性,运用基于一次二阶矩的混合几何误差精度可靠度分析方法,求解X、Y、Z轴3个运动方向的精度可靠性,以可靠度分析结果作为优化设计指标,全面地反映了几何误差对数控机床传动机构精度性能的影响; (3)通过可靠性灵敏度分析,具体量化各误差变量对数控机床传动机构精度可靠度的影响程度,通过机床传动机构精度分配优化,使数控机床传动机构的精度可靠性达到99.87%,成本降低34.74%,为数控机床传动机构的精度设计、参数选型提供了更为针对、高效、合理的理论依据。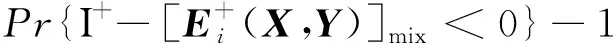
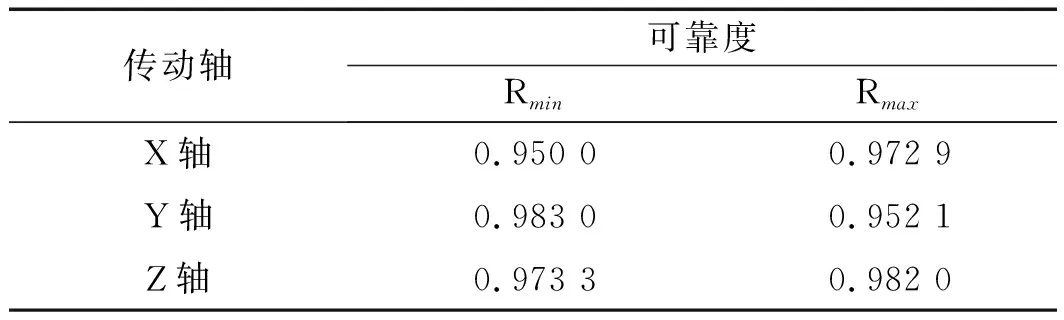
3 精度可靠性灵敏度分析及优化
3.1 精度可靠性灵敏度分析
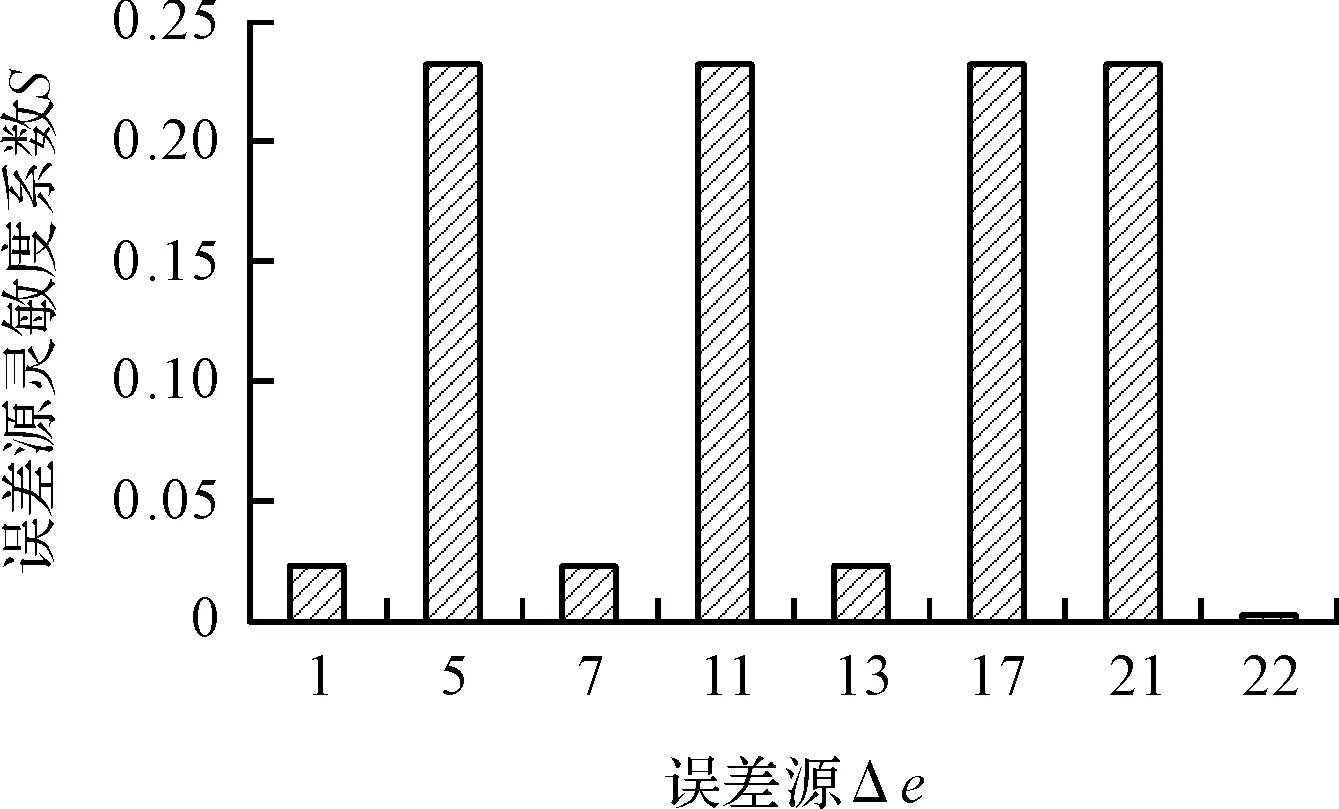
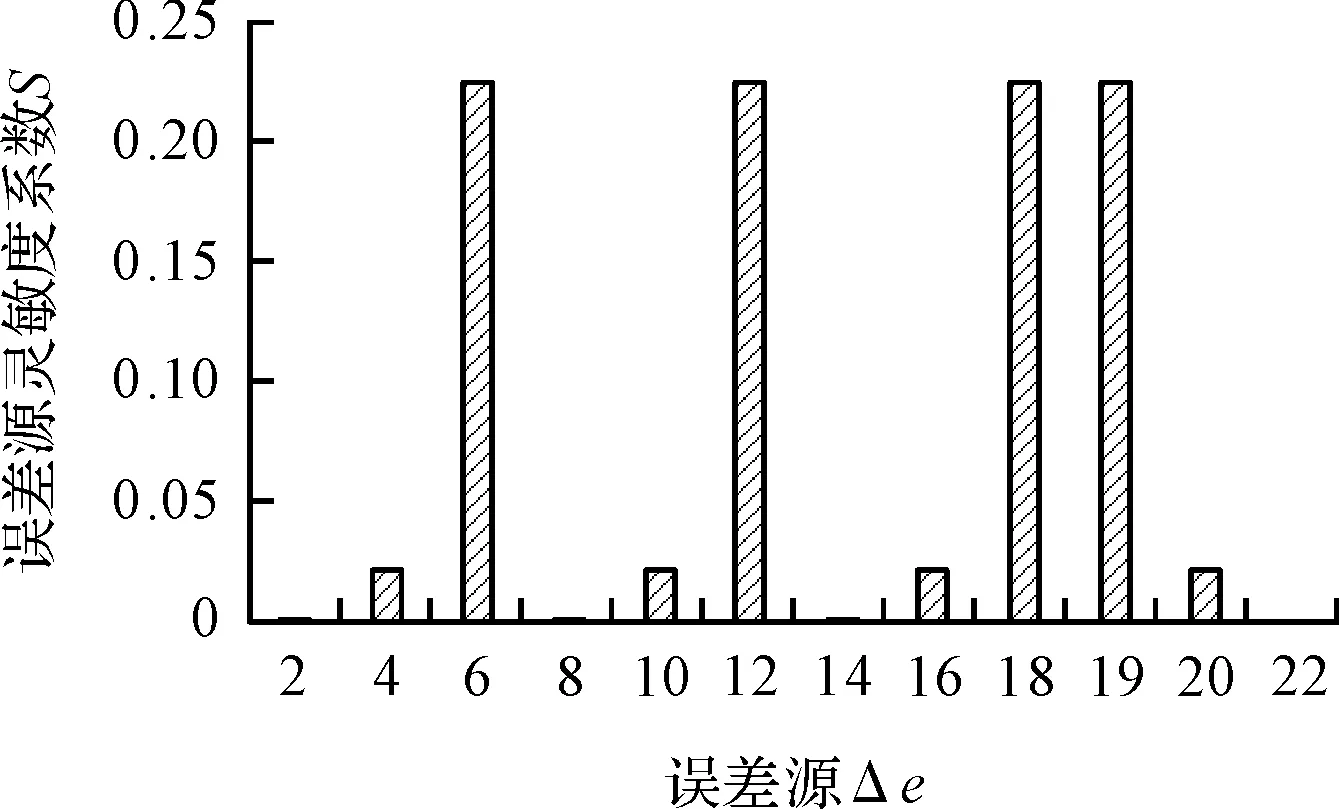

3.2 精度可靠性优化

4 结束语

