基于Fluent的船用防爆阀降压特性研究*

刘 红，沈少祥，蒋兰芳，闫 凡

(浙江工业大学 机械工程学院，浙江 杭州 310014)

0 引 言

作为大型柴油机必备的安全阀，船用防爆阀广泛应用于船舶、石化、煤矿等行业，尤其在船舶领域，国际船级社已经颁布了LACS UR M66技术规范[1]，明确规定新建的船舶发动机必须安装船用防爆阀。

目前，船用防爆阀的研究取得了一些成果：2000年王文权等人[2]对不同结构的船用防爆阀进行了试验研究，结果表明国产叠片式阻焰器设计制造是成功的；2006年黄立贤等人[3]在研究防爆阀设计过程中，成功开发了一套柴油机防爆阀爆炸试验装置，并取得了相关专利；2008年李潘宝等人[4]对防爆阀阻燃结构进行了改进；2009年KANG等人[5]对曲轴箱安全阀进行了流动特性的研究，通过试验比较验证了数值计算方法的有效性，采用运动网格策略可以很好地模拟了阀盘的运动和气体流动特性；2013年蒋兰芳等人[6]通过仿真研究了防爆阀的压力降情况，得到了压力降分析方法；2013年梁华等人[7]通过研究防爆阀散热特性和降压特性，初步解释了防爆阀机理[8]；2014年BAE等人[9]通过爆炸的流场变化研究了柴油机曲轴箱上的减压阀流动特性，有利于阻燃片的设计；2015年LEE等人[10]对防爆阀内的压力弹簧进行仿真与试验研究，提高了防爆阀性能；2016年AHN等人[11]对防爆阀阻燃片内的温度变化进行了研究。

目前，针对防爆阀的研究主要通过防爆阀性能试验完成，理论研究不足，因此本文将通过CFD技术对现有的某型防爆阀阻燃片进行降压特性研究，总结降压规律。

1 防爆阀仿真模型建立

1.1 防爆阀结构与工作原理

防爆阀结构如图1所示。

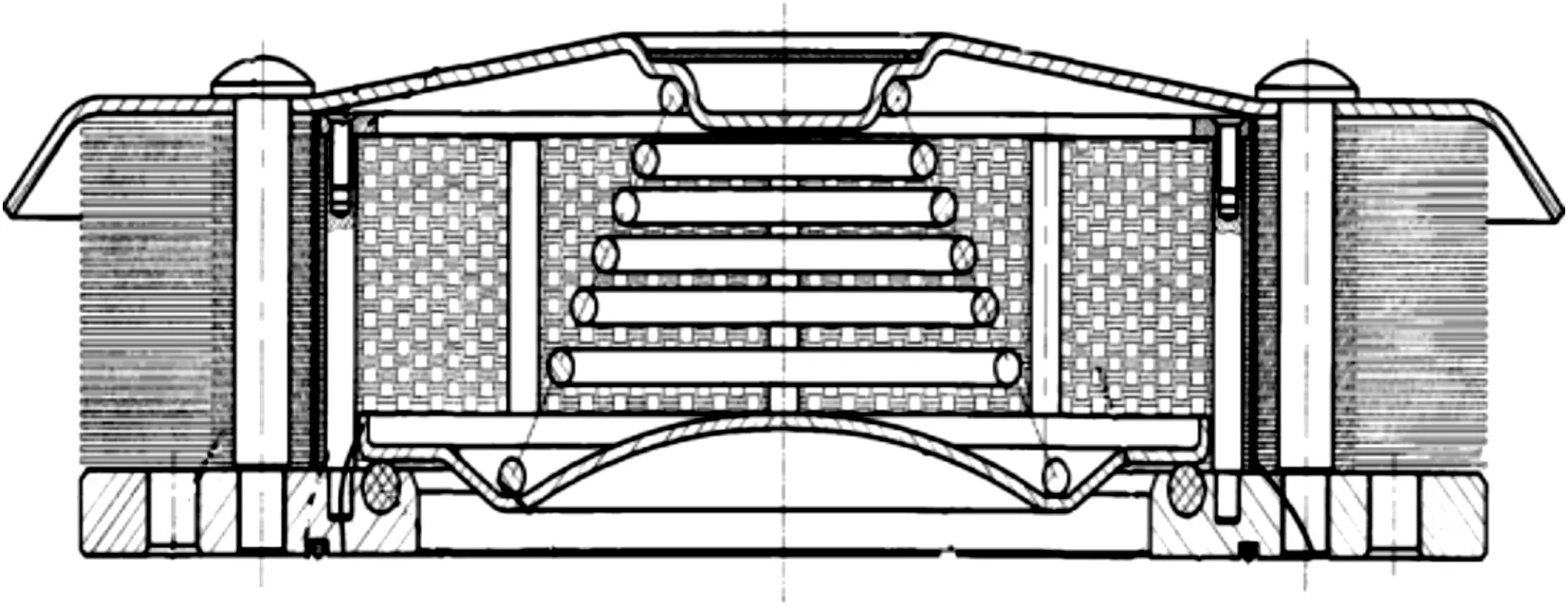
图1 防爆阀结构图

防爆阀由环形底座、面板、弹簧、阀板、阻燃器、内外阻燃圈等构成，其中阻燃器由冲压成型的阻燃片叠加而成，是防爆阀的关键部件。

防爆阀阻燃片与阻燃器如图2所示。

图2 防爆阀阻燃片与阻燃器

图2显示：阻燃片上有冲压成的凸台，凸台沿周向均匀分布，沿径向由内到外等间距均匀分布7圈，且相邻两圈的凸台相互交错分布，外圈凸台刚好挡在内圈两凸台形成的间隙前面。当高温高压的气流冲入流道，先受到凸台阻挡，与凸台碰撞损耗压力，与凸台壁面热交换降温，然后沿凸台左右方向分成两股气流，最后冲入下一个流道，这个过程不断重复直到冲出防爆阀，实现降压灭焰的目的。

1.2 模型假设

由于防爆阀内部流场较为复杂，本研究建立分析模型前作如下假设：

(1)防爆阀处于开启状态；

(2)气体是不可压缩的理想气体，湍流强度为5%；

(3)气体的热物性不变。

1.3 仿真设置

由图2可知：阻燃片具有周期性轴对称性质，故本研究取一扇面作为计算域，适当延长尾部作为延伸段用于观察气体流出防爆阀后的情况。计算域左端为入口，两侧是对称边界，延伸段为出口边界，其余为壁面边界。

防爆阀阻燃片计算模型如图3所示。

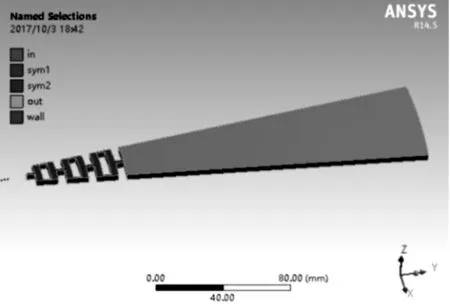
图3 防爆阀阻燃片计算模型

本研究采用ICEM软件进行网格划分，考虑近壁区和迷宫通道的复杂，采用非结构四面体网格，设置凸台壁面网格大小为0.1、0.3、0.5这3组，对应设置尾部延长部分网格大小为0.5、1、2这3组，分别得到309 852、256 632、165 842个网格单元。经仿真计算发现，3种网格质量对出口压强和温度的误差均在7%左右，网格对结果影响不大。本文取凸台壁面处网格大小为0.5，延伸段网格2，共165 842个网格。

阻燃片网格划分如图4所示。

图4 阻燃片网格划分

根据实际试验情况，防爆阀压力变化范围为0～0.35 MPa，故本文均匀选取10个压力值作为入口初始压力值，间隔为0.035 MPa，入口温度为2 323 K，其他关键设置如下：考虑近壁面对压力和温度的影响，开启能量方程，选择RNGk-ε湍流模型，勾选加强壁面计算选项，选择SIMPLEC算法进行运算，动量、湍流动能和湍流耗散率都设置为二阶迎风格式，以确保计算精度。

2 仿真结果分析

2.1 阻燃片降压分析

经过Fluent仿真分析，本研究获得所有初始压力下的压力变化。由于压力变化类似，本文取70 000 Pa初始压力图为例。

70 000 Pa初始压力下阻燃片压力场如图5所示。

图5 70 000 Pa初始压力下阻燃片压力场图

由图可知：(1)在不同入口压力的条件下防爆阀阻燃片内的压力场变化类似，红色区域表示压力值大，蓝色区域表示压力值小；(2)阻燃片内压力都是从入口到出口方向依次递减，呈现一个降压的趋势变化；(3)阻燃片外延伸部分压力变化不大，处于正常大气压下。

压力场出现以上现象可以从两个方面分析：防爆阀的设计角度分析，由于该防爆阀阻燃片结构上类似于迷宫式设计，层层凸台交相出现，气道连续而又急剧变化，使得气流与凸台、壁面发生剧烈碰撞，从而不断消耗能量，起到压力逐级降低的目的。压力降的角度进行分析，压力损失或压力降，是表示装置能量大小的经济指标，以装置进出口处流体的全压差表示。压力损失包括沿程压力损失和局部压力损失，其中沿程压力损失为流体在直管中流动时因流体具有的黏性而产生的压力损失，其值为：

(1)

式中：λ—沿程压力损失系数；v—平均流速；d—管道内径；l—管道长度。

局部压力损失为流体流经如阀口、弯道、通流截面变化等处所产生局部阻力引起的压力损失，其值为：

(2)

式中：ξ—局部压力损失系数。

结合阻燃片的结构可以看到，每层凸台间气道大小、形状都是变化的，压力损失系数也不同，导致高压气体经过这类迷宫式的结构中，压力损失明显，这就是防爆阀阻燃片降压机理。

2.2 降压特性分析

根据10组初始压力值的防爆阀仿真结果，将不同初始压力值下防爆阀阻燃片压力变化整理成表，具体压力变化如表(1，2)所示。

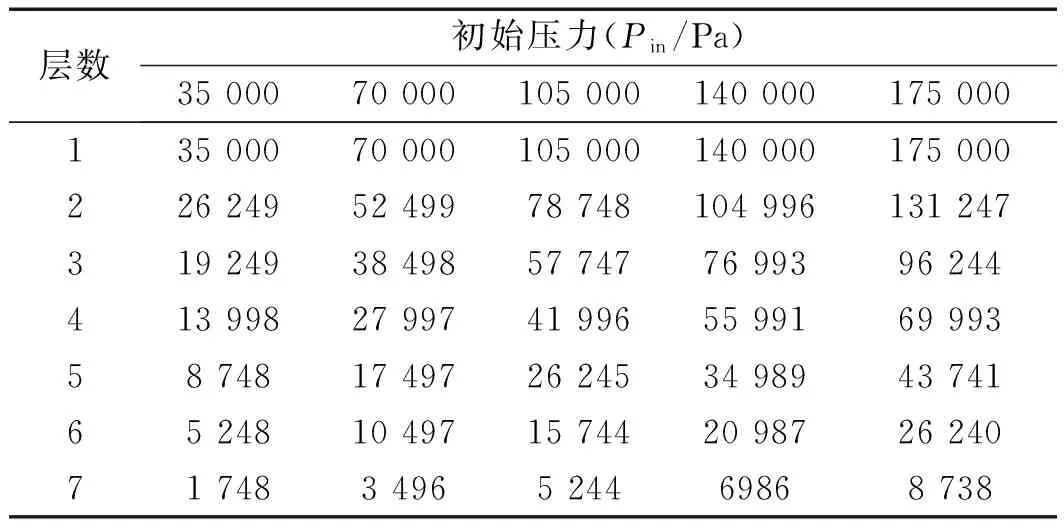
表1 前5组不同初始压力值下防爆阀阻燃片压力变化

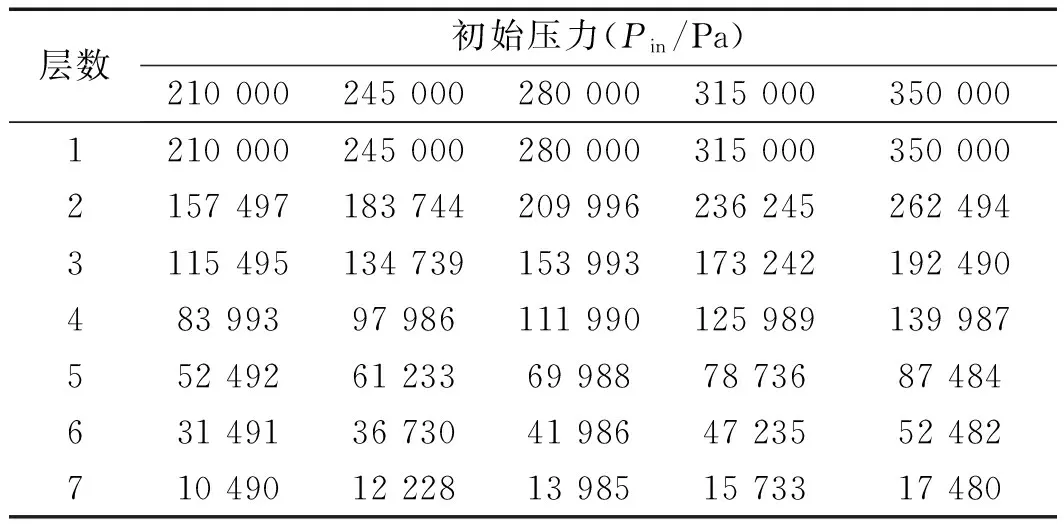
表2 后5组不同初始压力值下防爆阀阻燃片压力变化

通过表格1和表2可以发现：(1)从表格纵向看，压力随着层数的增加不断减小；(2)从表格横向看，由于入口压力不断增加，同一层的压力也不断增加。

根据这些发现，尝试将表格图表化，从而让数据更形象的表达规律。

将以上10组数据放入图中，如图6所示。

可以看到：(1)各组数据各自连成的线为曲线，遵循某种规律随层数下降，与文献[7]提到的直线略微不同，可能跟结构、尺寸变化有关；(2)初始压力值越大，曲线走势越陡峭，初始压力值越小，曲线走势越平缓。

为了探究压力随层数下降的规律，本研究使用Origin软件自动拟合功能，通过多次拟合尝试发现二次函数拟合效果最好，拟合效果指标R值都在0.99以上，各参数归类成表，拟合曲线参数值如表3所示。

图6 10组初始压力下的各层压力情况

初始压力(Pin/Pa)ABCR35 000520.92-9 605.243 7510.998 7270 0001 041.8-19 21087 5010.998 72105 0001 562.6-28 814131 2520.998 72140 0002 083.6-38 421175 0040.998 72175 0002 604.3-48 024218 7530.998 71210 0003 125.2-57 628262 5030.998 72245 0003 646.2-67 236306 2560.998 72280 0004 166.9-76 838350 0040.998 72315 0004 687.8-86 443393 7550.998 72350 0005 208.7-96 048437 5050.998 72

注：A，B，C—系数；R—拟合效果评价值，完全拟合时R等于1，下同

根据拟合结果来看，可以认为压力与层数的关系满足二次函数关系。

由于不同初始压力值下，各个圧力曲线的拟合函数是不同的，10组初始压力值将会有10个表达式反映阻燃片内各层压力的变化，为了综合探究不同初始压力、压力与层数的关系，需要将10个表达式整合为一个综合表达式。假设存在这样一个综合表达式：

Pn=(0.014 9Pin+0.061 3)n2+
(-0.274 4Pin-0.546 7)n+1.25Pin+0.733 3

(3)

为了使综合表达式完整可用，必须获得系数A、B、C所代表的值或表达式，即需要探究同一系数在不同初始压力值下它的数值变化规律，本研究将表2的数据放入图表中，系数A、B、C与初始压力关系如图7所示。

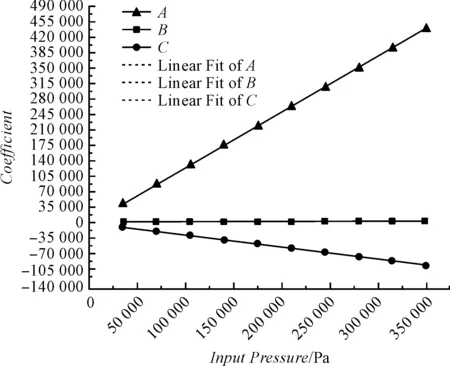
图7 系数A、B、C与初始压力的关系

根据图7可知：图中3条线为直线，即系数A、B、C与初始压力成线性关系，可以通过Origin软件将曲线线性拟合，获得如下3个系数表达式，其中拟合效果评价值R都等于1，说明3个系数与初始压力的关系非常符合一次函数，即：

Pn=(0.014 9Pin+0.061 3)n2+
(-0.274 4Pin-0.546 7)n+1.25Pin+0.733 3

(4)

Pn=(0.014 9Pin+0.061 3)n2+
(-0.274 4Pin-0.546 7)n+1.25Pin+0.733 3

(5)

Pn=(0.014 9Pin+0.061 3)n2+
(-0.274 4Pin-0.546 7)n+1.25Pin+0.733 3

(6)

式中：Pin—压力入口，以下通用。

将系数A、B、C的表达式(4～6)代入综合表达式(3)，可得到：

Pn=(0.014 9Pin+0.061 3)n2+
(-0.274 4Pin-0.546 7)n+1.25Pin+0.733 3

(7)

该规律公式仅适用于型号、结构、形状、尺寸等相同的阻燃片。

3 实验与结果分析

一般需要通过实验手段对比公式值与实验值的差别来验证规律公式的合理性。但是，一方面阻燃片有特殊性，国标中防爆性能实验只观察有无火焰窜出以判断防爆效果是否合格，并不直接检测各层压力变化。另一方面，阻燃实验是在瞬间完成的，检测爆炸瞬间气流经过防爆阀阻燃片的压力很难，只能通过观察火焰是否熄灭来检验其阻燃性能，但是在实践生产中，根据本规律公式来指导设计生产的阻燃片装配成防爆阀后经检验具有良好的阻燃性能。

为了验证该公式的准确性，本研究选择对比仿真值与公式值情况。在52 500 Pa～332 500 Pa间均匀取5组，间隔70 000 Pa，通过Fluent仿真分析，仿真压力值与公式值对比如表4所示。

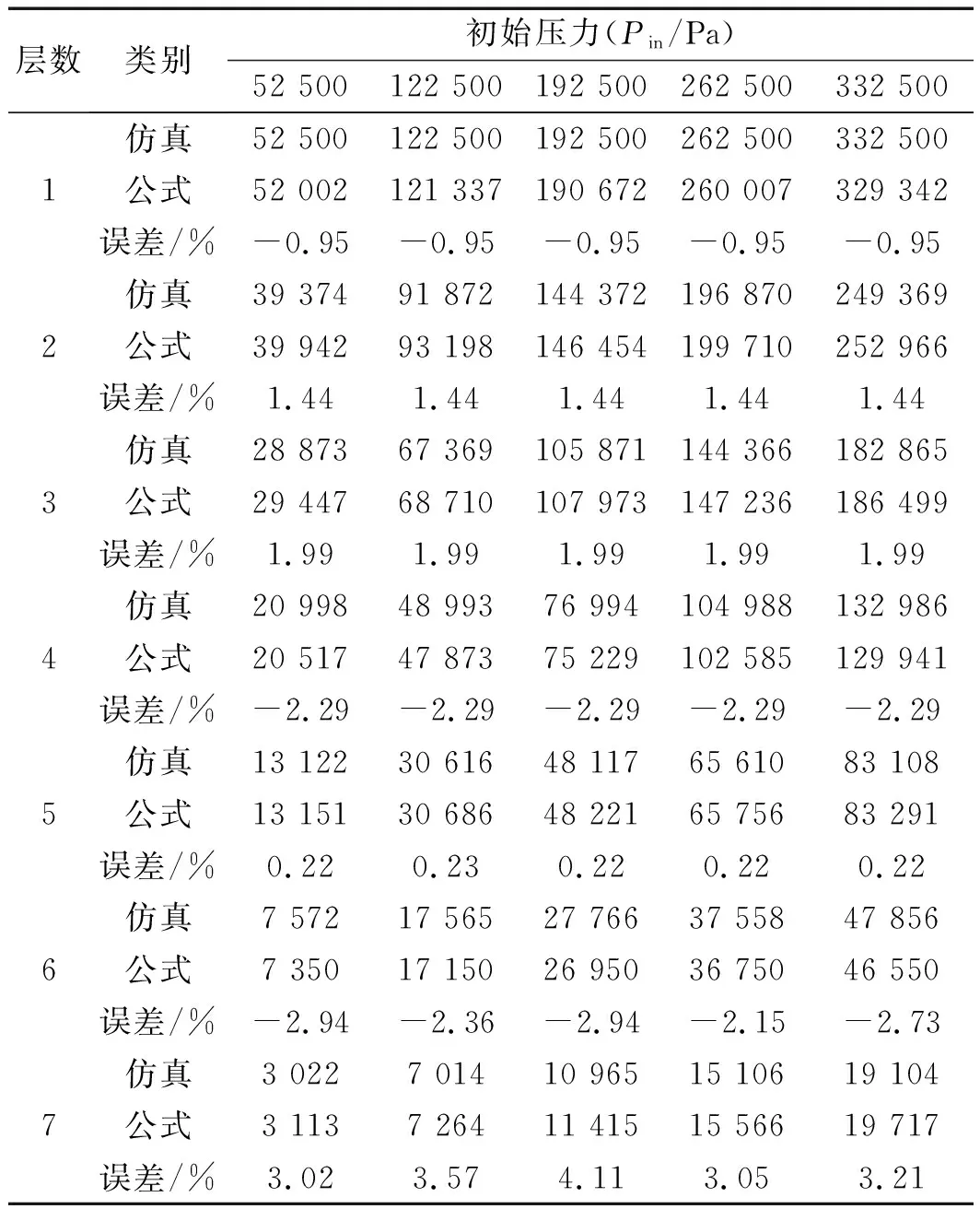
表4 防爆阀阻燃片仿真压力值与公式计算值对比

通过对比分析可以看到：该公式计算得到的压力值与仿真得到的压力值数量级相同，误差范围基本都在5%左右，说明该公式能够反映仿真情况，而且误差较小，可应用于防爆阀阻燃片的设计，且能够缩小防爆阀研发周期，同时也能够反映出阻燃片内部压力场的变化。

4 结束语

本文采用仿真方法研究了某型防爆阀阻燃片降压特性，通过降压分析，从理论上解释了阻燃片压力场出

现的沿程压力损失和局部压力损失与阻燃片内气道狭窄、结构布局等有关，通过进一步对10组数据的整理得到了阻燃片内压力与凸台层数的关系，进而得到了任意凸台所在处压力与初始压力、凸台层数的函数规律公式；为了验证公式的合理性，将公式值与仿真值进行对比，误差都在5%以内，基本能够反映阻燃片内压力变化。

通过该规律公式指导设计生产的阻燃片装配成防爆阀后，经国标性能试验检测，其防爆性能合格。故该研究成果可对防爆阀阻燃片的设计提供指导。