数学核心概念教学的思考与实践
文 广州市豪贤中学 张慧冰
数学核心概念往往以定理、法则、公式的方式表现出来,基本都是以文字叙述为主,这些核心概念具有高度的抽象性、概括性、简洁性和应用性,所以学生在学习过程中会存在一定难度。在教学中,应精心设计教学活动,把概念巧妙渗入学生学习过程中,引导学生学习并构建概念,逐步理解概念的本质。数学教学就是要让学生深入理解数学核心概念, 下面就如何有效的实施核心概念教学加以阐述。
一、创设情境,引入核心概念
初中数学概念,都是直接或间接地来源于现实生活,具有抽象性。对学生而言,实用性和实际性问题更能有亲切感和激发学习的好奇心。数学公式教学中,大部分教师容易出现两大教学误区:一是轻视公式的形成过程,只重视公式的套用;二是不重视公式的达成过程,只强调死记公式。完全平方和公式是初中整式教学的核心内容之一,完全平方和公式概念教学时,可创设源于生活的例子。
学校要修建一个边长为a米的正方形花坛,经过实地考察后,发现花坛还是小了一些,于是决定将边长扩大b米,现在请同学们帮忙算算扩大之后的面积是多少呢?
学生相互讨论后,小组派代表来讲解,一共有两种算法:
第一种:整体思想,每边扩大b米后仍是一个正方形,边长为(a+b)米,所以面积为:(a+b)2, 利用多项式与多项式的乘法法则可以很快计算出是 a2+2ab+b2。 第二种:分割考虑,结合画图,正方形增加了四个部分,四部分面积之和为: a2+ab+ab+b2=a2+2ab+b2。 学生通过观察,理解到完全平方和公式的几何背景:它是用不同的形式表示图形的总面积,并进行比较得来。
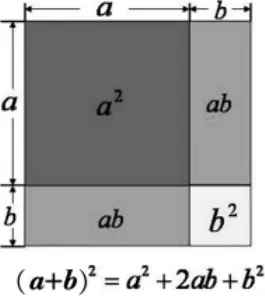
通过有实际背景的问题让学生感受生活中完全平方和公式的意义,培养学生观察—归纳—概括的数学能力,体会数形结合的思想方法,感知概念生成,提高学生学习数学的兴趣和运用知识解决问题的能力。
二、揭示本质,形成核心概念
形成核心概念的教学是整个核心概念教学过程中至关重要的一步。概念的形成是通过对具体事物的感知、辨析、抽象、概括出核心概念的过程,因此学生形成概念的关键就是发现事物或形的本质属性或规律。
如:多边形内角和公式概念课教学中,学生已经掌握了三角形的内角和是180°,对三角形的问题有一定的认识基础上,容易切入对多边形相关概念的探索,前后两者联系性较强。以三角形的内角和180°为基础,推导、归纳出四边形,五边形,…,n边形的内角和。
在四边形ABCD中,从A点出发,连接对角线AC,把四边形分割成2个三角形,那么四边形的内角和是 2×180°=360°。 同理可得,五边形内角和为 3×180°=540°,…,n边形内角和为 (n-2)180°。
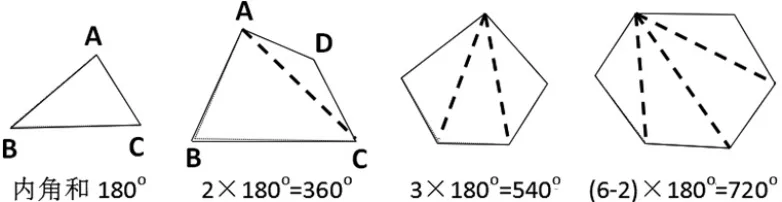
多边形内角和教学中,运用了从特殊到一般的观察方法,遵循从具体到抽象的认知,规律,将新的概念产生出来。数学中的一些概念是相互联系的,既有相同点,又有不同之处。辨析异同点,才能建立明确的核心概念。对于这类概念,运用猜想、类比等方法找出它们之间的联系和区别,使学生更加准确地理解和牢固记忆学过的核心概念。
三、运用概念,巩固核心概念
学习概念的目的是为了运用概念解决实际问题,把所学的知识运用到实践中,可以加深和巩固学生对数学核心概念的掌握。概念的巩固主要通过练习,练习题要有目的性、针对性、层次性、趣味性,使练习真正有助于学生理解新学核心概念,有利于发展学生的数学思维。练习包括了基本练习、变式练习和综合练习,每项练习都要有针对性,多层次、多角度的体现该节课新学的核心概念。课后作业对概念的巩固同样重要,设计作业时,重点概念反复练,设计对比练习,帮助学生分清容易混淆的核心概念,按照由简到繁、由易到难、由浅入深的原则,逐步加深练习的难度。
四、绘制概念图,强化核心概念
上世纪70年代末美国康耐尔大学的Novak首先提出概念图(concept map)这个新名词,并渗透到课堂上去。概念图是用来组织和表征知识的工具,它是由节点和连线组成的一系列概念,并且在连线上标注两个概念之间的相互关系。概念图直观的向大家展示知识的结构,梳理相关概念之间的联系,从而构建数学核心概念。老师可以让学生学习完一章节数学知识后,学生独立活合作方式完成概念图,构建章节知识体系,这样有助于学生深化理解所学内容的概念化、系统化理解。

